永磁同步电机参数自适应的建模与仿真
肖海峰,张 萌
(西安航空学院 电子工程学院,西安 710000)
目前,在线参数辨识方法中理论分析和试验效果已较为成熟,常用的主要有最小二乘法、模型参考自适应(MRAS)、卡尔曼滤波器、滑模变结构等[1-4]。其中的模型参数自适应参数辨识,主要通过已经得到辨识的系统参考模型构建可变的调节模型,再利用参考模型与可调模型二者之间的输出误差,通过特定自适应律的理论基础对可调模型的可变参数进行调整。文献[5]对永磁同步电机直接转矩控制系统的定子电阻采取在线辨识,采用了最小二乘法和模型参考自适应法;文献[6]基于RLS对嵌入式永磁同步电动机的定子电感、电阻进行在线辨识;文献[7]基于卡尔曼滤波器对PMSM定子电阻、直轴磁链和交轴磁链进行在线参数辨识。在此提出一种辨识系统模型方法实现对电机参数的估算。在永磁同步电机数学模型上,基于Popov超稳定理论,设计参数自适应律,在给定参考条件下建立矢量控制下的自适应参数辨识模型,通过MatLab软件对参数辨识过程进行仿真试验。
1 永磁同步电动机数学模型
PMSM产生旋转磁场的方法是通过永磁体励磁,但由于永磁体不同安装位置便有凸极式和内置式之分。这2种永磁同步电机的最大区别是,前者的交、直轴电感数值相等,而后者的交、直轴电感数值不相等。在此采用凸极式PMSM。基于三相静止坐标系得到电机的电压方程表达式
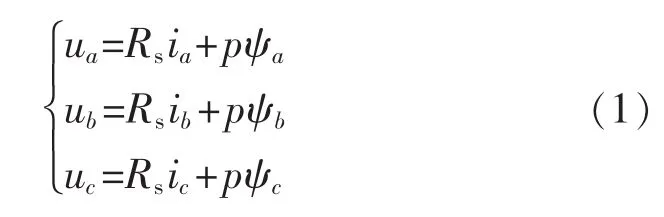
式中:p 为微分算子;Rs为定子绕组电阻值;ψa,ψb,ψc为三相绕组磁链;ua,ub,uc为定子绕组电压;ia,ib,ic为定子绕组电流。
d-q坐标系为旋转坐标系,在此以处于旋转状态下的坐标系为基准,对处于同样旋转状态下的电机进行建模,可忽略一部分时变因素。因此,电机状态方程中的系数在经过坐标变换后变为常系数,所希望得到的就是这个结果。凸极式永磁同步电动机的电机电压方程为

式中:id,iq为定子电流;ud,uq为定子电压;ωe为电角速度;ψd,ψq为永磁磁链。
2 参数自适应控制策略
以Popov超稳定理论为理论基础[8-10],在设计具有适应律灵活且结构清晰明确的特点的模型参考自适应系统时,也能够确保自适应的整个系统趋于稳定[11-13]。PMSM参数自适应辨识系统由线性前向方块与非线性时变反馈方块组成[14-15],通过该系统转化的非线性反馈系统是稳定的,这由Popov超稳定理论中可以清晰得到。满足Popov超稳定理论的积分不等式为
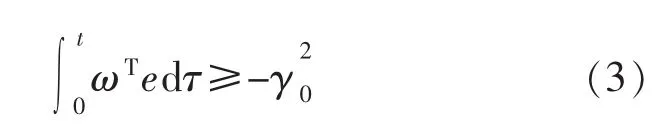
进一步行食管电生理检查,予心房S1S2程序刺激,设置S1S1间期为400 ms,S1S2间期为360 ms,S1S2间期每次递减10 ms,可诱发出心动过速,诱发窗口为S1S2 400/280 ms,诱发出心动过速与自发心动过速一致(图4),予频率为250 次/min的S1S1连续刺激可终止心动过速。期间患儿未诉心前区不适,无头晕、黑蒙、晕厥,无呕吐等不适。考虑患儿年龄小,为首次发作,但发作时心率明显增快,遂予酒石酸美托洛尔片10 mg/d口服以预防心动过速发作,定期门诊随访,必要时行射频消融术。随访半年,无复发。
选择的可调整参数模型的自适应律(比例积分形式)分别为

式中: f1, f2,g1,g2,h1,h2为各自相应的自适应律函数;初值为(0);初值为(0);初值为(0)。

式中:Kf1,Kg1,Kh1分别为自适应律的积分增益;Kf2,Kg2,Kh2分别为自适应律的比例增益;ed为两相旋转坐标系 d 轴电流偏差,ed=id-d;eq为 q 轴电流偏差,eq=iq-q。
对可调参数不断优化调整,便可通过该稳定系统中的参数可调节模型实时追踪实际电机系统,从而在系统趋于稳定的前提条件下,就认为实际电机系统可由该参数调整模型表示。因此,实际电机系统中的参数就可通过之前设计好的参数可调模型如实反映。可令

当系统趋于稳定时,可以根据式(8)(9)及式(10),并通过可调参数求得永磁同步电机模型参数
假设同步电机转速ω为已知量,在状态方程的基础上构造参数调节模型,即

其中

3 系统模型仿真
3.1 系统仿真建模
在Popov超稳定理论的基础上,通过理论分析可以构成稳定的系统模型。该模型由建立的参数可调整模型与剖析推导出的参数自适应律构成,整体结构如图1所示。
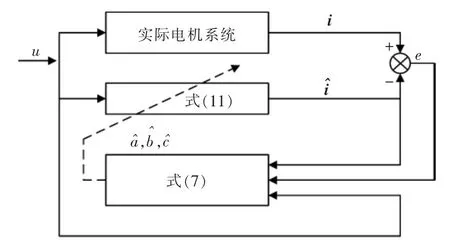
图1 参数自适应辨识系统结构Fig.1 Structure of parameter adaptive identification system
参数自适应在线辨识器的5个输入量分别为转速、直轴定子电流、交轴定子电流、直轴电压以及交轴电压,存在于参数辨识模型中ud和uq。其中,uq为永磁同步电机在q轴上实际定子电压分量;ud为d轴上实际定子电压的分量。
将系统结构在MatLab/Simulink环境下进仿真,可得到如图2所示的永磁同步电动机矢量控制下系统的整体模型。参数自适应律模型如图3所示。
3.2 仿真结果分析
仿真和试验中电机的参数设定如下:
定子电阻Rs=0.9585 Ω;
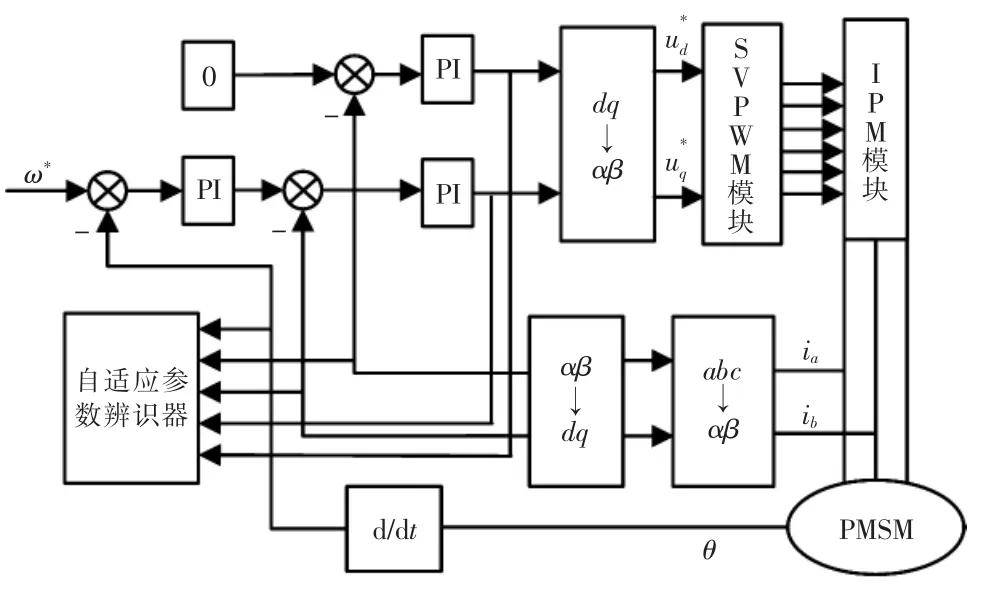
图2 矢量控制下PMSM参数自适应辨识模型Fig.2 Adaptive identification model of PMSM parameters under vector control
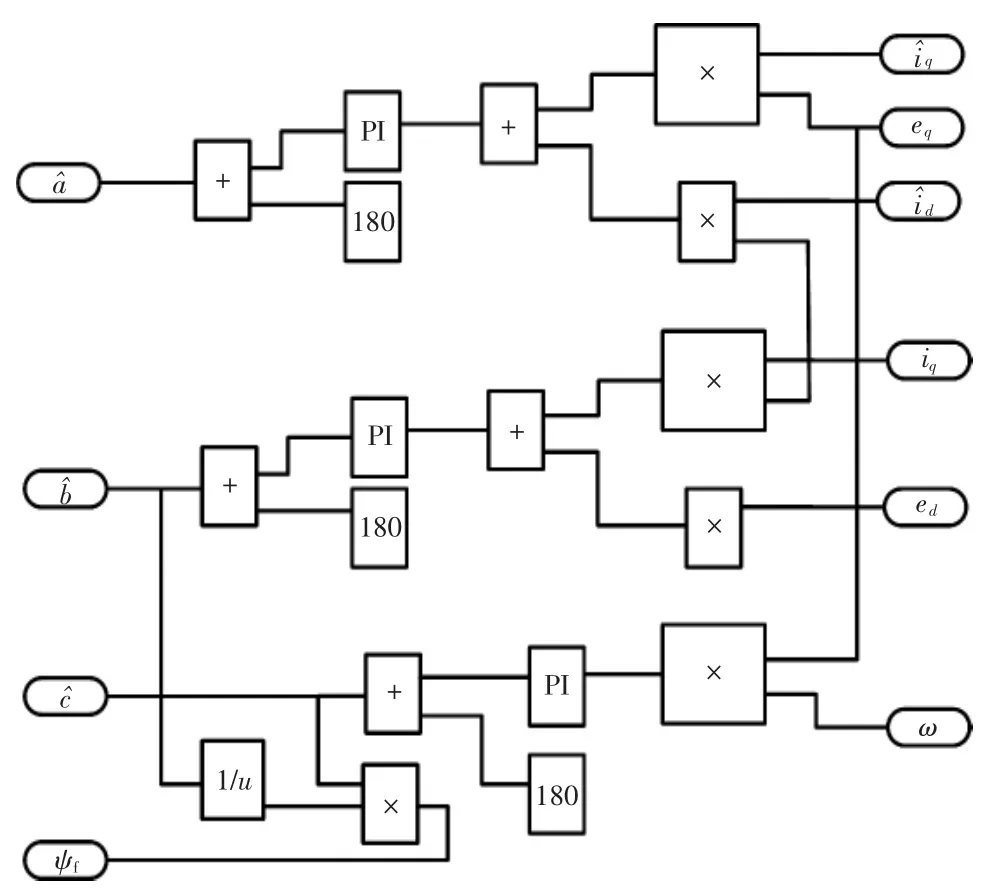
图3 参数自适应辨识律模型Fig.3 Parametric adaptive identification law model
交、直轴电感Ld=Lq=5 mH;
转子磁链ψf=0.1827 Wb;
电机转动惯量 J=6.329×10-4kg·m2;
极对数p=4。
仿真试验结果如图4所示。所测电阻辨识值的误差为9.1%,电感辨识值的误差仅为4.2%,永磁磁链辨识值的误差为8.6%,与理论值比较接近,表明自适应律辨识值的误差很小。
4 结语
仿真结果与之前验证的永磁同步电机的参数辨识结果相同。文中提出的永磁同步电机参数自适应辨识方法可以获得电机电阻、电感和转子磁链。基于波波夫稳定理论获得的模型参数自适应律在辨识电机参数时可以满足更快速和准确的要求。

图4 仿真试验结果Fig.4 Simulation test results

