磁控管供电LLC谐振变换器分析与设计

沈佳磊，陈家新

（1.东华大学 信息科学与技术学院，上海 201620；2.东华大学 机械工程学院，上海 201620）

开关电源技术已有几十年的历史，早期产品的开关电源频率低，成本昂贵，功耗大，仅用于尖端电子设备。近些年来，电力电子技术有了高速的发展，对于开关电源的要求也相应提高了，要求效率高、噪声低等[1-2]。由于半桥LLC谐振变换器不仅拥有串联谐振变换器的优点，而且还具有并联谐振变换器的优点，因此逐渐成为了国内外专家的研究对象。半桥LLC谐振变换器的结构简单，可以实现软开关，且可以利用变压器的漏感来实现效率高、功率高和EMI低等特点[3]。在此，分析研究半桥LLC谐振变换器的原理，建立起稳态数学模型，确定半桥LLC谐振变换器的各主要参数，最后通过MatLab搭建仿真模型进行分析验证。

1 LLC谐振变换器工作原理

1.1 LLC谐振变换器主电路原理

半桥LLC谐振变换器的主电路如图1所示。图中，Vin为输入电压，该电压是220 V交流电经过整流滤波之后得到的稳定直流电压；Q1和Q2为2个开关管，一般是MOSFET，它们互补导通并且防止有互通的状态，常在2个开关管之间留有一定的死区时间；Coss1和Coss2是2个开关管中寄生电容、缓冲电容以及各种杂散电容合并后的等效电容；Cr为串联谐振电容；Lr为串联谐振电感；Lm为变压器的励磁电感；T为高频变压器，其右侧为倍压整流滤波电路，为负载磁控管提供高压直流电。

图1 磁控管供电电源主电路原理Fig.1 Principle of the magnetron power supply main circuit

图中，Cr，Lr和Lm组成LLC谐振电路。当变压器的电压为上正下负时，二极管D1导通，D2反向截止，此时电流通过二极管D1给电容Co充电，并且为负载供电；当变压器的电压为上负下正时，二极管D2导通，D1截止，此时电流通过二极管D2为电容Co充电，同时给负载供电，由此最终得到的电压是输入电压的2倍。另外，在此电路中电容Co既有储能的功能，也有一定的滤除纹波功能，使得到的输出电压更加平滑。

1.2 LLC谐振变换器工作原理

LLC谐振变换器电路有2个谐振频率，一个是谐振电感Lr和谐振电容Cr谐振产生的串联谐振频率fr，另一个是励磁电感Lm加上谐振电感Lr与谐振电容Cr谐振产生的串并联谐振频率fm。即

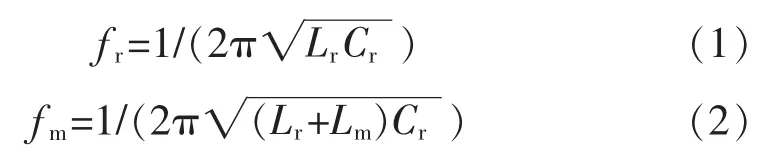
半桥LLC谐振变换器共有4个工作状态，即开关频率 f＜ fm，fm＜ f＜ fr，f=fr和 f＞ fr。当 f＜ fm时，此时整个谐振变换器呈容性状态，无法实现零电压开通，由此造成的开关损耗较大，一般不适用。当fm＜f＜fr和f=fr时，半桥LLC谐振变换器可以实现零电压开通，且在关断时实现变压器副边的零电流关断。当f＞fr时，半桥LLC谐振变换器虽然能实现零电压开通，但是不能实现变压器副边的零电流关断。

2 LLC谐振变换器的稳态分析

2.1 基波分析法

半桥LLC谐振变换器的直流输入是占空比为D，幅值为Vin，频率为f的方波电压。其输入电压VN用傅里叶级数展开，可以得到

式中： f为开关频率。 基波分量 VN，FHA（t）为

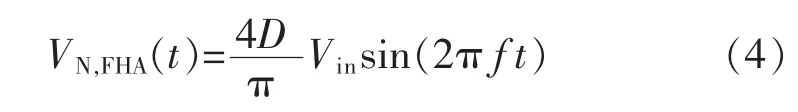
因此其基波分量的有效值为

且其输入电流irt是一个正弦波，可以设为

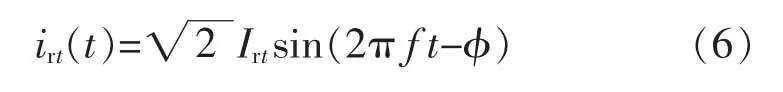
式中：Irt为输入电流的有效值；φ为谐振电流与电压的相位差。

因为在LLC谐振变换器电路中，输出电路是倍压整流电路，因此其输出电压是一个幅值为Vo的方波，且输出电流与输出电压是同相位。

方波电压的傅里叶级数为

式中：φ为输出电压与输入电压的相位差。可以得到Vo，rect（t）的基波分量为

由此得到基波分量的有效值为

整流电流的整流分量为

式中：Irect为整流电流基波分量的有效值。故可得输出的平均电流Io为

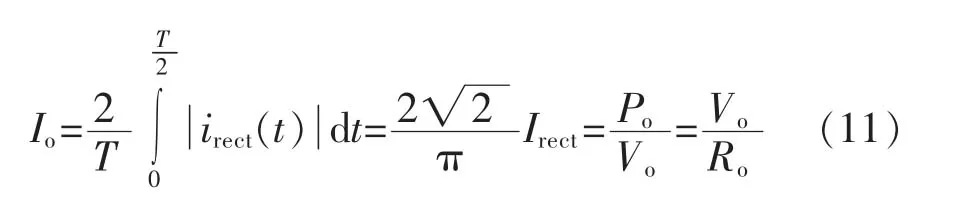
式中：T为开关管的周期；Po为当输出电阻为Ro时的输出功率。 由于 Vo，FHA（t）和 irect是同相位的，因此可以把滤波网络等效成一个等效电阻，即

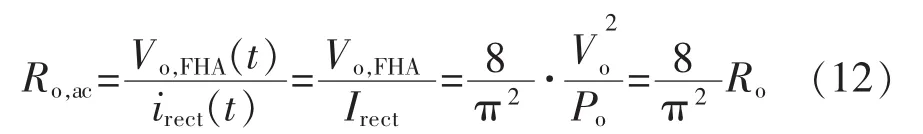
将其折算到变压器的原边，得到

从而得到的LLC谐振变换器的等效电路，如图2所示。

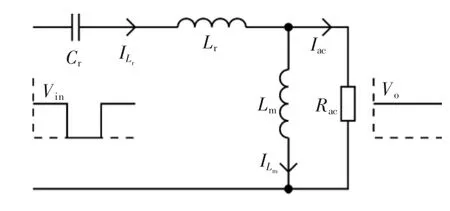
图2 LLC谐振变换器部分等效电路Fig.2 Partial equivalent circuit of LLC resonant converter

由图2得到的LLC谐振变换器等效电路的输入输出传递函数为

故可得

即可以得到其直流增益为

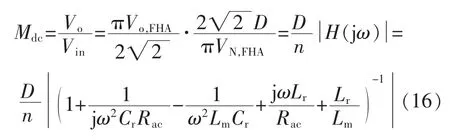
由此可以将式（16）化简为 λ，Q，fn的表达式，即

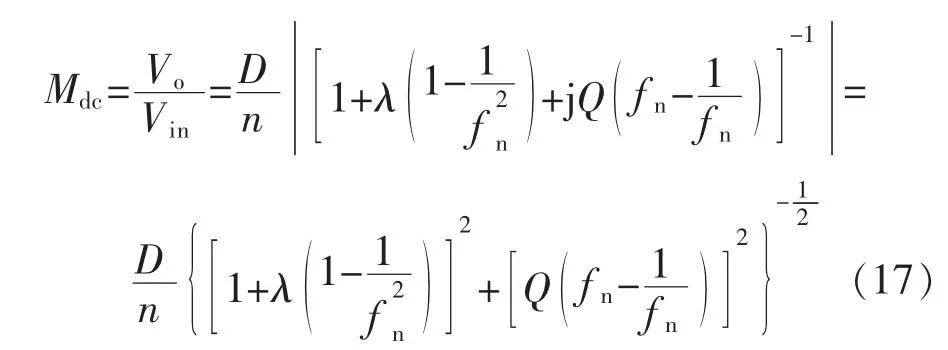
至此完成半桥LLC谐振变换器的直流增益公式推导。

2.2 LLC输入滤波电路分析

半桥LLC谐振变换器整体等效电路如图3所示。

图3 LLC谐振变换器整体等效电路Fig.3 Integral equivalent circuit of LLC resonant converter

根据功率公式可知

磁控管的有效工作电压范围是2800～4200 V，半桥LLC谐振变换器的输出电压为［3500+700sinα］V，其有效值为3535 V。因此可以得到其输出功率为（3535×3535/16000）W=780 W，即 Po=780 W。

在设计半桥LLC谐振变换器时，考虑实际使用中会有一定的功率损耗，在此设其效率为85%，即η=85%[4]。根据输出功率以及效率，可以得到半桥LLC谐振变换器的输入功率为

输入电压U=220V，求得滤波电感L上的电流为

根据输入电压和输入电流，求得整个LLC谐振电路网络的等效阻抗为

考虑到功率因素的问题，功率因素越大越好，因此设功率因素为1，即cosφ=1。也就是说LLC谐振变换器的等效阻抗是一个纯阻性负载。根据式（12）（13），可知

式中：n为变压器的变比；Ro为输出负载。根据等效电路及电路原理，可得

式中：ωs为半桥LLC谐振变换器的角速度；ω为220 V交流电压经过整流桥后的角速度；实部Rm=52，虚部Im=0。

3 主电路参数设计

3.1 LLC谐振网络参数设计

磁控管只有在电压为2800～4200 V时才能够正常工作，在其他电压范围都无法正常工作[5]。在此设计的开关频率为（20～40）kHz。

根据前述半桥LLC谐振变换器的直流增益分析可得，直流增益随着开关频率的增大而减小。因此，在开关频率最小时，其输出电压应小于4200 V；在开关频率最大时，其输出电压应大于2800 V。

假设滤波电容C上的电压为100～230 V，要满足磁控管的输出电压要求，所需的具体限制见表1。

表1 宽输入工作电压设计依据Tab.1 Design basis for wide input voltage

励磁电感Lm不仅要满足输出效率的最大化，还要满足半桥LLC谐振变换器实现零电压开通的条件，因此Lm需满足

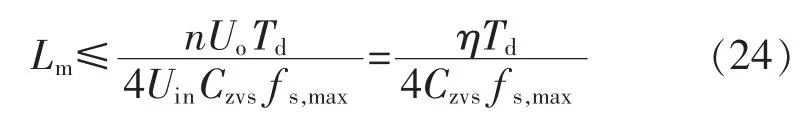
因取效率η=0.85，由经验值可知设驱动信号的死区时间 Td=2 μs，寄生电容近似为 Czvs=0.2 μF[6]，可以计算出励磁电感Lm=53 μH。在随后具体试验的基础上最终确定励磁电感Lm=35 μH。

由此确定了励磁电感Lm的参数，且磁控管的负载为16 kΩ[7]，因此在励磁电感Lm已知的情况下，通过前述的半桥LLC谐振变换器直流增益公式和表1具体要求，求出谐振电感Lr，谐振电容Cr以及变压器变比n的具体数值。在此可解得Lr=23 μH，Lm=35 μH，Cr=1.4 μF，n=1∶16。

至此完成半桥LLC谐振变换器核心参数的计算。

3.2 滤波电路参数设计

根据分析，半桥LLC谐振变换器要实现零电压开通，Lm，Lr，Cr和输出阻抗 Rac所构成的谐振电路必须呈感性负载。由于功率因素的要求，即要求半桥LLC谐振变换器的整个电路（包括LC滤波电路）呈纯阻性负载。

在式（23）总电阻计算公式中，Rac=5.6×104π；Rm=52；Im=0；ωs=2 π×20000～2 π×40000；ω=2 π×100。

因为ωs是一个变化的范围，且ωs的改变会导致Lm，Lr，Cr和输出阻抗Rac所构成的谐振电路也是一个变化的值。因此，文中在不同ωs的情况下，分别求出其相应的LLC谐振阻抗值，再对其取加权平均作为最后的半桥LLC谐振变换器的谐振阻抗值[8]。

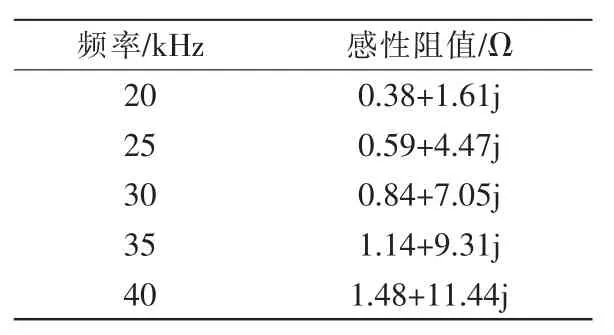
表2 不同频率下LLC谐振阻抗值Tab.2 LLC resonant impedance at different frequencies

可得

即

式中：ω=2 π×100。 可求得最终结果为 C=238 μF，L=20 mH。

4 仿真模型建立及仿真结果

4.1 MatLab仿真模型建立

基于MatLab/Simulink平台搭建的LLC谐振变换器的仿真模型如图4所示。该模型分为3个部分，整流电路、开关网络、谐振网络和倍压整流网络。

图4 半桥LLC谐振变换器模型Fig.4 Model of the half-bridge LLC resonant converter

4.2 仿真结果及分析

整流输出电压和滤波电感L上的电流波形如图5所示。

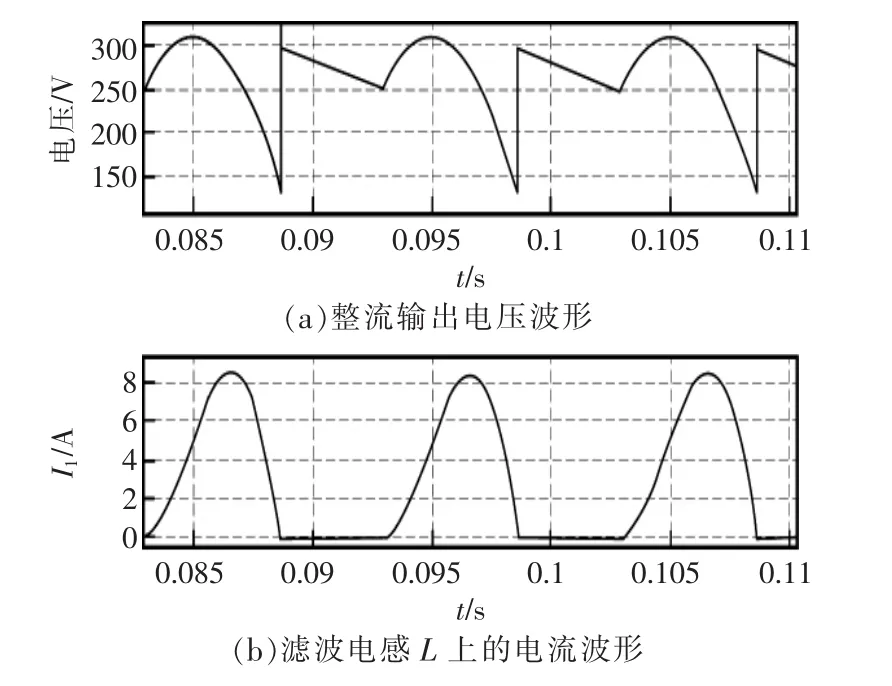
图5 输出波形1Fig.5 Output waveform 1

由图可见，整流输出的电压波形为140～310 V。输出的电感电流近似为1个占空比为60%的正弦波，其峰值电流约为9 A，仿真得到的电感L上的有效电流约为3.8 A，与计算所得4.2 A存在些许误差，但是在误差的允许范围内；且计算出其功率因素为 0.975（ f=30 kHz）。

输出负载的波形如图6所示。由图可见，输出电压在3500～4000 V，满足磁控管2800～4200 V的工作范围，因此所设计的参数能够满足设计要求。

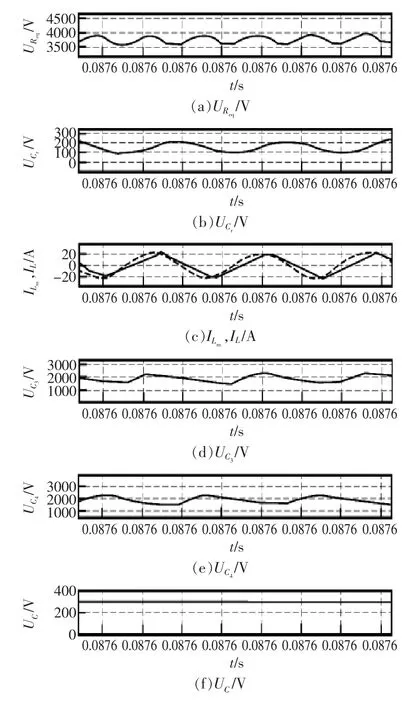
图6 输出波形2Fig.6 Output waveform 2

5 结语

采用半桥LLC谐振变换器和倍压整流相结合的方式设计了一款磁控管供电电源，利用基波分析方法对半桥LLC谐振电路建模分析，然后完成核心参数设计与滤波电路的参数设计，并且利用MatLab/Simulink进行建模仿真，验证理论设计的正确性。仿真结果证明该设计方案可以让半桥LLC谐振变换器主电路可靠高效工作，可以作为负载磁控管的供电电源。