局部符合逻辑对反应堆保护系统可靠性的改善作用

彭 勇，张 庆，许 标，吴礼银

（核反应堆系统设计技术重点实验室，成都 610213）

反应堆保护系统执行安全级功能，是核反应堆仪表与控制系统的重要组成部分。反应堆保护系统是否可靠，直接关系到反应堆能否安全运行。当前，反应堆保护系统的总体符合逻辑最常用的架构方案是 2oo4（即四取二）和 2oo3（即三取二）[1]，这是安全系统长期发展的结果。除了总体符合逻辑之外，系统供应商还采用局部符合逻辑技术，以进一步降低系统自身设备失效而导致安全功能拒动或误动作的概率。通过定性分析，可以推断局部符合逻辑对改善系统可靠性有积极作用[2]，但对相关参数改善了多少，尚未有具体的数据。在此，基于马尔可夫分析法对2oo3系统进行定量分析[3-5]，将考虑局部符合逻辑后的系统模型计算结果与一般2oo3系统模型计算结果进行比较。分析结果相对于其他架构而言具有一定的代表性，希望通过文中的分析为系统设计提供理论支持。

1 系统原理

1.1 反应堆保护系统架构原理

考虑到可靠性模型的复杂程度，文中选择2oo3架构的反应堆保护系统作为研究对象，系统总体架构如图1所示。系统有 3个通道（IP，IIP，IIIP），假设每个通道有输入模块DI，处理模块CPU，输出模块DO各一个。DI采集现场信号；CPU对DI采集信号进行定制比较以生成用于局部逻辑符合的脱扣信号，每个通道的脱扣信号同时用于其他2个通道的局部逻辑符合，通过局部逻辑符合产生通道输出命令；DO按照输出命令输出通道级保护信号；3个通道的保护信号进行2/3（即三取二）表决，最终实现反应堆保护动作。

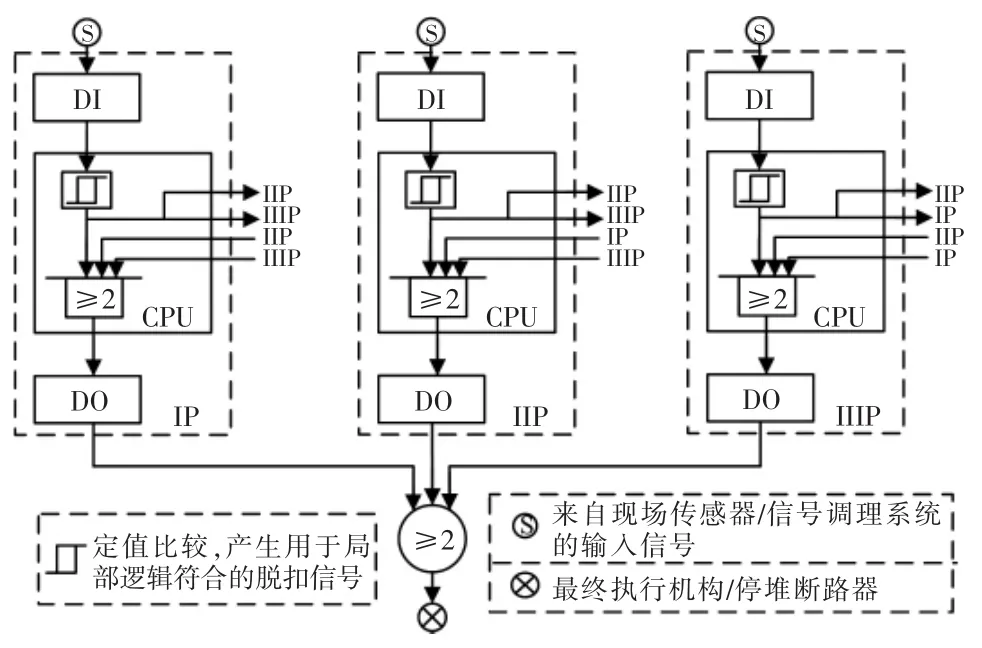
图1 反应堆保护系统架构Fig.1 Reactor protection system architecture

1.2 局部符合逻辑降级

反应堆保护系统的2/3局部符合逻辑按照表1给出的降级机制进行逻辑降级。每个通道CPU中的局部符合逻辑，按照无效脱扣信号的数量，进行相应机制地逻辑降级或触发所在通道的保护信号。

表1 局部符合逻辑降级机制Tab.1 Degradation mechanism of local conforming logic

2 马尔可夫模型

为了观察局部符合逻辑的作用，将反应堆保护系统按照标准的2oo3系统和采用局部符合逻辑的2oo3系统，分别建立马尔可夫模型。

2.1 标准2oo3系统模型

标准2oo3系统3个通道完全独立，没有信号交互，每个通道信号流按照DI→CPU→DO进行处理，最后3个通道的保护信号参与总体2/3表决。标准2oo3系统的马尔可夫模型如图2所示。

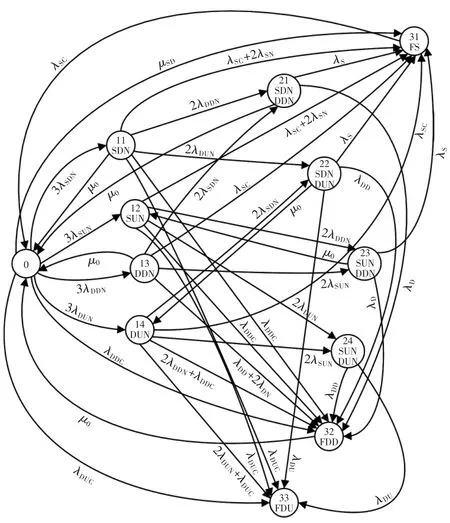
图2 标准2oo3系统状态转移Fig.2 State transition of the standard 2oo3 system

马尔可夫模型中，用圆圈表示状态，带指向的弧线表示转移方向；分别用失效率λ或修复率μ表示转移率；状态0为初始状态；状态11—14分别表示3个通道有1个发生失效；状态21—24分别表示有2个通道各发生1种失效模式；状态31—33分别为系统安全功能处于系统安全失效FS状态、系统危险可诊断失效FDD状态、危险不可诊断失效FDU状态；以安全S/危险D+可诊断D/不可诊断U+共因C/非共因失效N的形式，区分通道失效类型和失效率类型。

相比一般的马尔可夫模型，文中在此基础上进行了一些修改，使计算结果更加保守：对有2个通道失效的中间状态若只有1个通道发生可诊断失效，则不再通过维修返回状态0，而是只能维修好被诊断到失效的通道，例如图2中的状态22和状态23。

2.2 采用局部符合逻辑的2oo3系统模型

对于采用了局部符合逻辑的2oo3系统，为了简化模型，需要对系统结构进行划分。如图3所示，系统划分为前后两部分：输入部分为采用局部符合逻辑的2oo3结构，每个通道信号流按照DI→1/2CPU进行处理，局部符合逻辑能够进行逻辑降级；输出部分为标准2oo3结构，每个通道信号流按照1/2CPU→DO进行处理，最终表决逻辑不进行逻辑降级。输入部分和输出部分为串联结构，因此可以分别对两部分建立马尔可夫模型。其中，输出部分的状态转移与图2相同。

输入部分的状态转移如图4所示。图中，虚线圆圈表示的状态31—33与实现圆圈代表的状态31—33相同。由于采用局部符合逻辑的2oo3结构中，当参与表决的脱扣信号无效时（诊断到失效），局部符合逻辑会进行降级，因此图中状态11，13，21，23，24 和 26 的局部符合逻辑均降为 1/2。降级机制的存在将使部分原本指向状态32（FDD）的失效转而指向状态31（FS）。例如：转移路径11→31，状态11有1个通道已经发生SDN，符合逻辑降级为1/2，若再有1个通道发生DDN，则触发保护信号，转移到状态31。

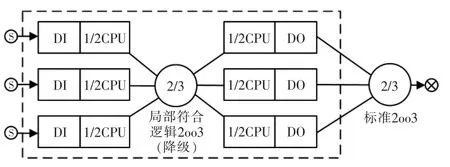
图3 采用局部符合逻辑的2oo3系统划分Fig.3 Partition of the 2oo3 system within local conforming logic

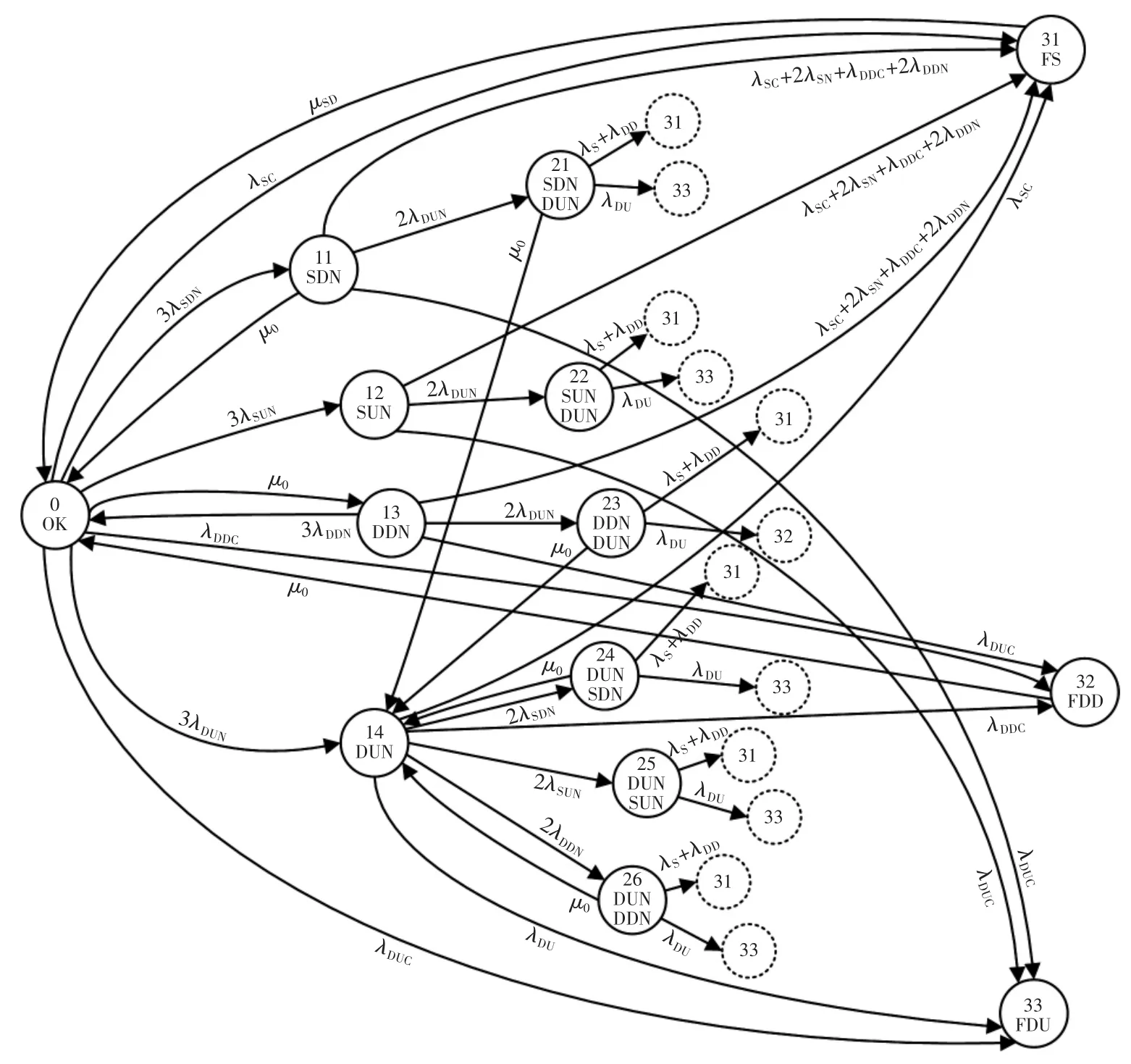
图4 采用局部符合逻辑的2oo3结构状态转移Fig.4 State transition of the 2oo3 structure within local conforming logic

2.3 计算原理

2.3.1 拒动概率和误动概率

文中以拒动概率（也就是危险失效概率）PFD，avg和误动概率（也就是安全失效概率）PFS，avg，作为可靠性的表征参数，对反应堆保护系统的可靠性进行研究，它们分别体现了系统安全功能发生危险失效和安全失效的概率。通过马尔可夫模型计算PFD，avg和PFS，avg的方法，即通过求极限状态概率矩阵得到极限状态（稳态）下的危险失效概率和安全失效概率。文献[6]提供了一种线性代数解法，其具体步骤是：先根据状态转移图写出状态转移矩阵，再用表示初始状态为0状态的初始行矩阵反复乘以状态转移矩阵，得到极限状态下的概率矩阵，将系统危险失效状态或系统安全失效状态的概率相加，即可得到目标结果。

2.3.2 串联模型的概率

采用了局部符合逻辑的2oo3系统可以视为一个串联模型，则系统的失效概率就等于输入部分失效概率与输出部分失效概率之和。

3 概率计算与分析

3.1 系统拒动概率和误动概率计算

代入以下输入数据，对反应堆保护系统拒动概率和误动概率进行计算：DI和DO安全失效率均取λS=2500 fit， 危险失效率 λD=500 fit；CPU 安全失效率取 λS=1500 fit，危险失效率 λD=500 fit；模块失效的诊断覆盖率为90%；修复率μ0=0.125/h，系统误动作后的重启率μSD=（1/24）/h；周期性检验时间TI=18个月；按照文献[7]的方法，得到2oo3架构可诊断的共因失效因子β=1.5%，不可诊断的共因失效因子βD=0.75%。

反应堆保护系统拒动概率和误动概率计算结果见表2。表中，A为标准2oo3系统的失效概率；B为采用局部符合逻辑的2oo3系统的失效概率；（A-B）/A为概率的变化率。若不考虑共因失效的影响，得到的结果见表3。由表2和表3可知，局部符合逻辑对反应堆保护系统的 PFD，avg和 PFS，avg均有一定改善效果，特别是对减小由非共因失效导致的系统拒动概率有明显效果。

表2 反应堆保护系统的 PFD，avg和 PFS，avgTab.2 PFD，avgand PFS，avgof reactor protection system

表2 反应堆保护系统的 PFD，avg和 PFS，avgTab.2 PFD，avgand PFS，avgof reactor protection system

3.2 敏感性分析

使用3.1给出的输入数据，对采用局部符合逻辑后 PFD，avg和 PFS，avg的变化率（A-B）/A 进行敏感性分析。

3.2.1 诊断覆盖率DC的影响

其他条件不变，仅改变诊断覆盖率DC，对A系统、B 系统的 PFD，avg和 PFS，avg进行比较， 得到的曲线如图5 所示。 随着 DC 的提高，PFD，avg和 PFS，avg的变化率均减小，且 PFS，avg的变化率比 PFD，avg大。 显然，DC较低时，局部符合逻辑的改善作用较大；DC越高，局部符合逻辑的改善作用越小。

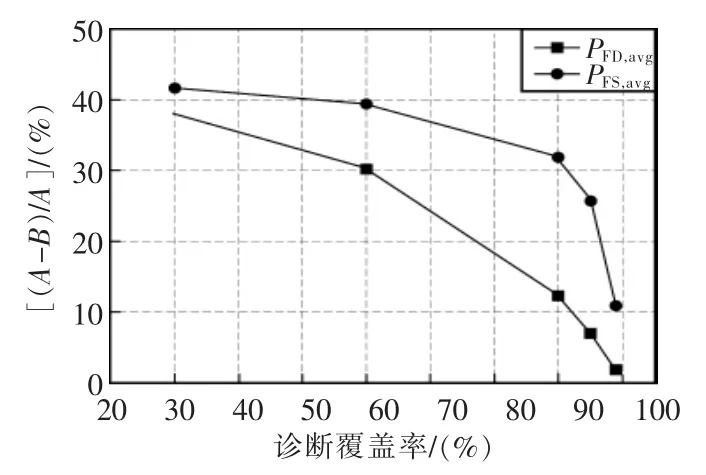
图5 诊断覆盖率DC对（A-B）/A的影响Fig.5 Influence of DC on （A-B）/A

3.2.2 λi/λo的影响

λi和λo分别为单通道的输入部分和输出部分的失效率。通过调整DI和输入部分1/2CPU的失效率大小，以改变λi/λo的值，在此过程中单通道的λS/λD不变，得到图6所示的曲线。输入部分失效率占整个单通道失效率的比重越大，B相对于A的PFD，avg变化率越大。而对于 PFS，avg，当 λi/λo＜1 时，其变化率随 λi/λo的增大而增加；当 λi/λo＞1 时，变化率反而开始减小，但仍大于0。此外，由图6可见，当λi/λo小于某个值时，局部符合逻辑对PFS，avg的改善作用更大，λi/λo超过该值时，对 PFD，avg的改善作用更大。

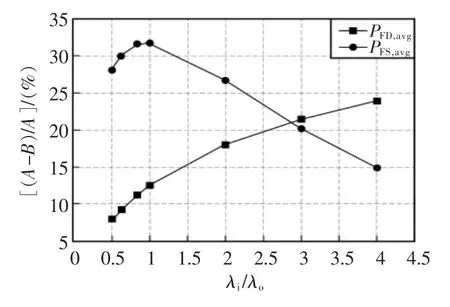
图6 λi/λo对（A-B）/A 的影响Fig.6 Influence of λi/λoon （A-B）/A

3.2.3 λS/λD的影响

保持输入模块DI总失效率不变，通过调整DI安全失效率和危险失效率的比例，改变单通道的λS/λD值，得到图7所示的曲线。随着安全失效率占通道失效率的比例增加，PFS，avg的变化率也在增大，PFD，avg变化率减小。可以推测，局部符合逻辑对 PFD，avg和PFS，avg的改善作用大小，与参与局部符合的安全失效率和危险失效率比例有关，占通道失效比例越大的失效类型，局部符合逻辑对其改善作用越大。

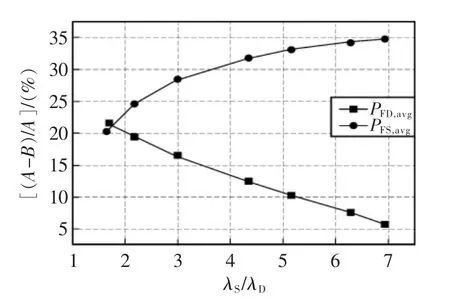
图7 λS/λD对（A-B）/A 的影响Fig.7 Influence of λS/λDon （A-B）/A

4 结语

综上所述，采用局部符合逻辑有利于改善反应堆保护系统可靠性，对降低系统安全功能的拒动概率和误动概率都有明显效果。对于通道自诊断能力差的系统而言，局部符合逻辑可以一定程度上弥补低诊断覆盖率的不足，使系统自诊断能力大大提高。当单通道输入部分的失效率低于输出部分，或高出不多时，局部符合逻辑对误动概率的改善作用更大；而当输入部分的失效率明显高于输出部分时，局部符合逻辑对拒动概率的改善作用更大。对安全和危险2种不同失效模式，局部符合逻辑对占通道失效比例越高的失效改善作用越高。

局部符合逻辑对不同架构类型系统可靠性的改善程度可能有所区别，但是，具有提高诊断能力、降低拒动概率和误动概率的优点是确定的。此外，在系统设计过程中还需要评估采用局部符合逻辑可能引起的通道独立性降低，增加通道间通信而引入的新的失效，以及产品成本等问题。因此，目前局部符合逻辑技术更多的应用于安全系统或对可靠性要求高的设备，也许在不远的将来能够推广到更多领域中。