对称间隙单自由度振动系统的Simulink仿真

崔锦涛，汪 诤

（兰州交通大学 机电工程学院，兰州 730070）

实际机械系统中广泛存在着各种非线性因素，因此工程实际中的振动系统绝大多数属于非线性系统。近些年来，人们对于实际工程中含间隙振动系统的问题越来越重视[1-4]。

对于非线性振动问题的求解，多借助于数值方法[5-8]，但是这种方法往往需要编制复杂的计算程序，也会借助多提动力学软件进行仿真，然而软件仿真往往针对特定的模型进行的（例如齿轮系统、连杆机构、链传动等）[9-11]。对于一些特定的模型，大型通用多体动力学软件往往没有相应的模型。因此，要想通过多体动力学软件进行非线性问题的仿真并得到较为精准的结果，还是需要与其他方法（有限元分析、过程控制）相结合进行联合仿真。

软件本文将在对称间隙碰撞系统模型基础上，实现了一种基于Simulink的含间隙非线性动力学仿真模型。与传统的数值仿真算法程序相比，Simulink是一种框图式的动态系统建模仿真工具，可以实现多个变量同时输出显示，并且在模型运行过程中动态显示变化过程。并且，此方法对于实现Simulink与多体动力学软件进行含间隙类非线性动力学联合仿真提供了参考意义。

1 物理模型和数学模型

典型的对称间隙单自由度碰撞模型如图1所示。质量块M通过弹簧（K0）阻尼（C）系统连接，振子M在简谐波激励的作用下沿着水平光滑平面运动。设线性弹簧在完全释放时的位置为零点，以零点建立向右的一维坐标系统。当振子的位移＞B（或＜-B）时，受到刚度为K1的弹性约束，在简谐力的作用下，如此往复发生碰撞。

图1 对称间隙单自由度碰撞模型Fig.1 Single degree of freedom collision model with symmetrical gap

1.1 数学模型

图1所示对称间隙单自由度振动系统为典型的非线性振动系统。其主要含有分段线性弹性力F（X），其数学模型为

分段线性弹性力为

取无量纲化参数为

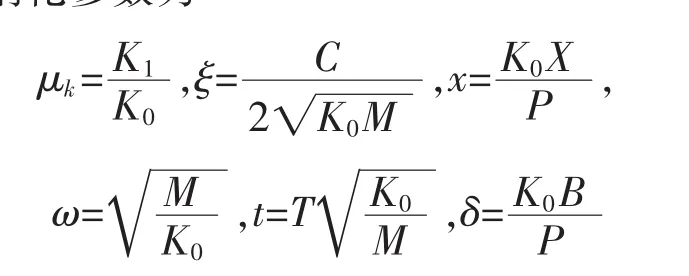
则无量纲化形式为

其中

1.2 分叉图

取式（2）中的参数 μk=32，ξ=0.23，δ=0.02。 采用龙格库塔法对系统进行数值积分，得到系统的分岔图如图2所示，图中横坐标为激振频率ω，纵坐标为振子运动到坐标零点时的瞬时速度。由图可见，系统对ω的变化极为敏感，并且随着激振频率的改变，系统出现了周期三分岔、混沌、倍化分岔、周期运动等特性。

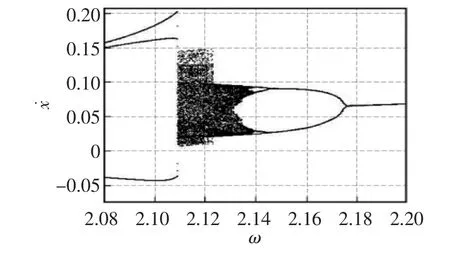
图2 分岔图Fig.2 Bifurcation diagram

为了更好地描述分岔图中这几种典型的运动特性，取 ω 分别为 2.1，2.115，2.166，2.188；对系统进行数值仿真，得到了周期三分岔、混沌、倍化分岔、周期运动相对应的相图，如图3所示。

图3 系统在不同激振频率下的相图Fig.3 Phase diagram of system on different excitation frequency

2 Simulink建模及仿真

Simulink可以实现建模、仿真、动态分析的可视化仿真工具，以各种类型的子模块可以搭建出线性系统、非线性系统，以及数字信号处理系统。一般来说，1个动态Simulink系统的构成分为3个部分，即信号的输入、主系统、系统的响应。文中使用连续系统模块Continuous，数学运算模块Math Operations，信号源模块Source等，搭建出对称间隙单自由度碰撞系统的模型，并使用信号流路模块Signal Routing确定系统的稳态输出；利用双标量图形模块XY Graph绘制系统相图[12-14]。

2.1 积分模块设计

在Simulink中，由微分方程建立仿真模型通常有3种方法：①将微分方程转换成传递函数Discrete TransterFcn；②将微分方程转换成空间状态方程State-Space；③利用过程信号连续时间积分模块Integrator直接建模。在此采用方法③。

其中

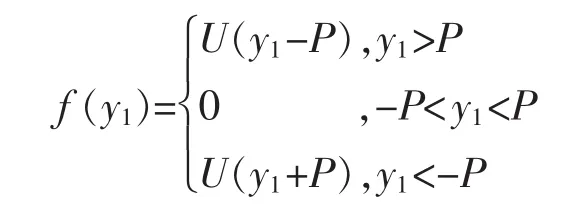
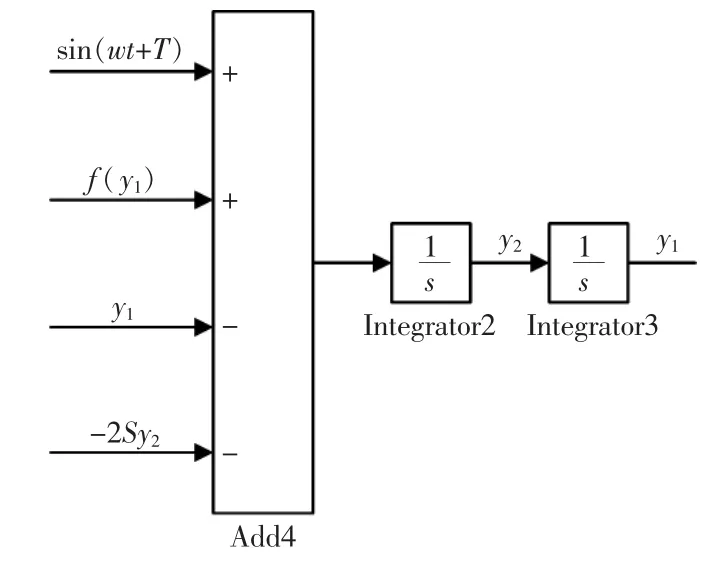
图4 积分模块Fig.4 Integral module

2.2 非线性模块设计

非线性部分即式（3）中的 f（y1），对其进行转换，得

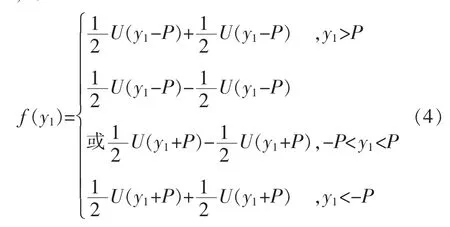
式（4）中的数学运算可采用Math Operation模块库中的Product数据相乘模块、Add信号相加模块实现；分段逻辑关系可采用Commonly Used Blocks模块库中的Switch模块实现。Switch模块基于第2输入端（中间）的值，判断输出第1输入端（上部）还是第3输入端（底部）。当第2输入端的值大于模块阈值（P值）时，第1输入端作为输出；反之第3输入端作为输出。

由于Switch模块的通过判断标准Criteria for passing first input，仅包含中间输入是否大于等于阈值（U2≥Threshold），因此对式（4）中的定义域做如下转变：

其中，采用Gain信号增益模块，对输入信号x取负增益可以得到-x。

3 Simulink仿真

Simulink中模块的仿真过程可以解释为模块不断地接受信号、更新状态和计算输出过程。同样，模型的仿真是系统在特定的仿真时间段内不断根据源信号计算状态和输出的过程。连续时间系统的仿真过程是将连续的时域离散成相应的采样时间点，然后通过数值积分的方式求解响应，Simulink将采样时间点分为主时间步和微时间步2类，后者是对前者的进一步细分。

连续时间系统中的离散状态更新仅发生在主时间步上，而在2个主时间步之间保持不变。同时，在仿真结果输出中，Simulink只显示主时间步的状态和输出（实际上主时间步的结果是微时间步上数值积分累积而成的）。微时间步上进行的工作，则是计算连续状态的微分以更新连续状态，同时计算每个模块的输出。

系统的仿真一般经历模型的初始化和仿真执行2个阶段。

初始化阶段在此阶段Simulink将进行以下操作：

1）模块的参数估值。模型中很多模块都具有参数（可能是变量或表达式）其具体值由MatLab确定。

2）模型的各个子系统被展开，取而代之的是一个大系统，然后模型中的模块按更新次序排序（即仿真执行时的顺序）。模块的更新顺序存在2个原则：①每个模块必须在它所驱动的任何一个模块更新之前更新；②非直接馈入模块可以按任何次序更新，只要它们在其所驱动的直接馈入模块之前更新。

3）确定每个模块输入输出信号的属性，诸如数据类型、数值类型、信号宽度（标量、向量或矩阵）。若模块没有明确的信号属性，Simulink采用属性传递的方法确定待定模块的特性，即未知模块的属性由驱动它的模块属性唯一决定。

4）确定模型中所有模块的采样时间，分配和初始化用于存储每个模块状态和输出当前值的存储空间。

模型执行阶段在模型的执行阶段Simulink通过数值积分实现仿真。所运用的仿真解法器取决于模型提供它的连续状态的微分能力。计算微分可以分成2步：首先，按照排序所确定的次序计算每个模块的输出；然后再根据当前时刻其输入状态来确定状态的微分，得到微分向量后再将其返回解法器，后者用它计算下一采样时间点的状态向量。一旦新的状态向量计算完毕，被采样的数据源模块和接收模块才被更新。

Simulink提供给用户一系列的数值积分器。对于连续时间系统，根据步长的变化情况分为固定步长和可变步长两大类：1）固定步长求解器 ODE1（一阶 Euler法）、ODE2 （二阶改进 Euler法）、ODE4（四阶Runge-Kutta法）；2）可变步长求解器 ODE45（四五阶 Runge-Kutta法）、ODE23（二三阶 Runge-Kutta法）、ODE113（二三阶 Adams-Bashforth 法）。

选用ODE45作为积分求解器，系统的信号输出采用双标量图形输出模块XY Graph，第1坐标量输入y1，第2坐标量输入y2；为了得到系统稳态响应，以系统仿真时间为信号，采用输出选择开关（Switch）控制阈值的方法控制信号输出。根据数学模型，将模块输入输出参数之间正确连接，最终搭建完成对称间隙单自由度振动系统的Simulink仿真模型，设计如图5所示。设置参数U=32，S=0.23，P=0.02；仿真参数设置如下：

图5 Simulink中的仿真模型Fig.5 Simulation model use Simulink

仿真开始时间为0/s；

仿真停止时间为200/s；

取样开始时间为100/s；

取样停止时间为200/s；

最大步长为0.02；

最小步长为0.001；

求解器为Ode45（Dormand-Prince）；

相对误差为10-6；

绝对误差为10-6。

取正弦信号（Sine Wave1）频率分别为2.1，2.115，2.166，2.188；运行模型得到不同激振频率下的相图，如图6所示。

图6 Simulink模型中仿真的相图Fig.6 Simulation phase diagram use Simulink model

4 结语

采用Simulink可以建立与对称间隙单自由度振动系统数学模型完全等效的仿真模型，建模过程简单，不需要复杂繁琐的编程；以分模块的方式建立系统（包含积分模块、非线性模块、时间控制模块），使得庞大的动力模型构建过程变得简单易行。Simulink具备优秀的积分算法和丰富的求解器类型，可以达到数值计算的精度水准，能够满足工程实际应用。Simulink的示波器可以实现动态实时显示图像的特点，并且在运行过程中可以调整模型参数进行假设仿真分析，监视参数变化对运动特性的影响。这种方法的效率要高于程序计算，且操作简便。