滑模变结构控制光伏最大功率点跟踪的研究
张洪斌,马文飞,李晓东
(安徽理工大学 电气与信息工程学院,淮南 232001)
世界经济迅速增长,使得人们对能源的需求也日益增加,传统化石能源存储量有限且易对自然环境产生破坏,为了避免这些不利影响,人们将目光转向了清洁无污染的新能源领域。太阳能作为新能源领域的重要组成部分,具有存储量巨大且易于获得等优点,从而成为世界各国重点开发和研究的对象。然而,在利用太阳能时也存在一些问题,如光强、温度等外界环境参数是不可控的,它们随着时间的变化而呈现一种非线性变化,这就使得太阳能电池的输出功率不能时刻保持稳定,即光伏发电系统不能始终工作在最大功率点处,从而会造成系统振荡及电能损失。因此,需要在光伏系统中利用最大功率点跟踪MPPT控制技术,使系统能够快速稳定地工作于最大功率点处,然而,传统的MPPT控制方法难以同时满足快速性和稳定性的要求。为此,文中提出一种基于滑模变结构的控制策略来实现快速稳定的跟踪最大功率点,设计出相应的滑模控制器,并用李雅普诺夫函数对其的稳定性进行判定分析,由于滑模控制器可自行设计且不受环境参数及无关扰动的影响[1],这就使得滑模变结构控制与传统的扰动观察P&O法相比具有更好的稳定性能。同时,引入幂次趋近率提高系统的跟踪速度,并将其与等效控制相结合,提高控制系统的动态品质。
1 光伏电池建模及特性分析
光伏电池是光伏发电系统的核心组成部分。它是用于承担将太阳能转变为电能的装置,其基本原理是当太阳光照射到光伏电池板上时,由于光伏电池具有较多的P-N结,其P区和N区在光子撞击的作用下,会产生较多的电子-空穴对,在结电场的影响下,电子会源源不断地向N区靠拢,空穴会不断地向P区靠拢,从而形成光生电场,实现太阳能向电能的转换。一般情况下,单个伏电池的输出电压较低,在实际应用中大都是将多个光伏电池单元以串并联的形式构成光伏阵列,用以满足工程需求。光伏电池的理想等效电路的结构如图1所示。
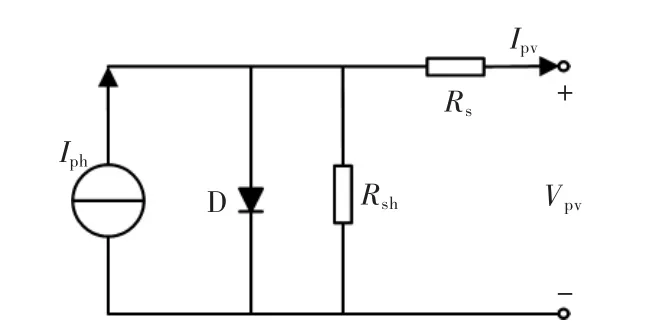
图1 光伏电池等效电路Fig.1 Photovoltaic cell equivalent circuit
光伏电池输出电流为
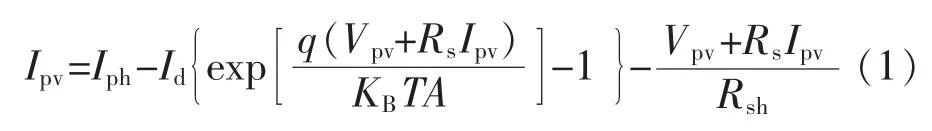
由于Rs较小,而Rsh较大,于是有
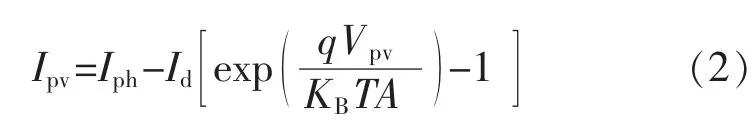
式中:Ipv为光伏电池的输出电流;Iph为光生电流;Id为二极管的反向饱和电流;Rsh为内部并联电阻;Rs为串联电阻;KB为玻尔兹曼常数;T为光伏电池的绝对温度;A为光伏电池PN结的理想因子。
为了便于光伏电池的特性仿真,可假设Iph=Isc,式中Isc为光伏电池短路时的电流。根据式(2)可以建立光伏电池在工程应用中常用的数学模型[2],即
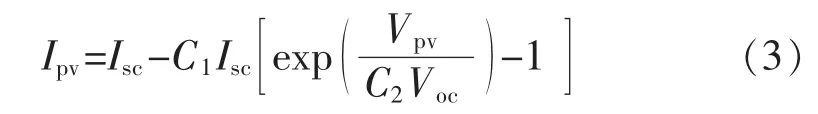
其中
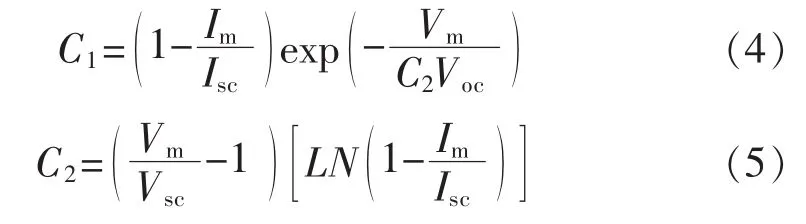
式中:Voc为开路电压;Vm,Im分别为最大功率点处电压、电流。由简化的工程数学表达式可以看出,只需知道 Voc,Vm,Isc,Im这 4 个参数就可以在 MatLab 中搭建模型进行仿真。于是得到的不同温度和光照强度下的V-P仿真结果分别如图2和图3所示。
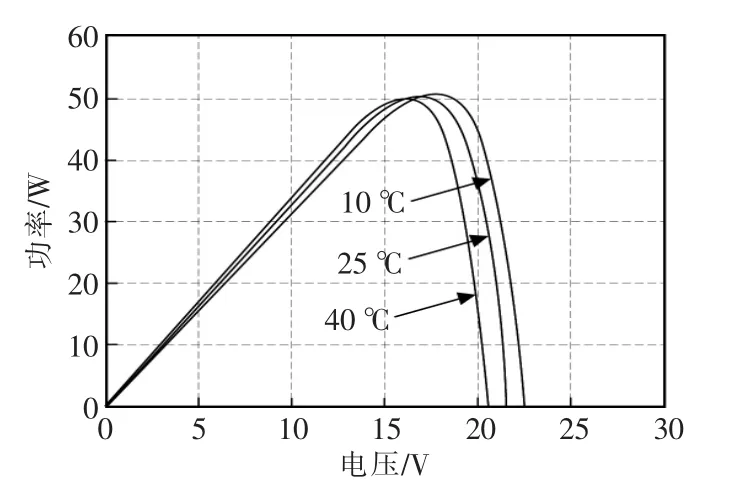
图2 光照强度恒定(1000 W/m2)不同温度下V-P曲线Fig.2 V-P curve at different temperatures with constant light intensity(1000 W/m2)
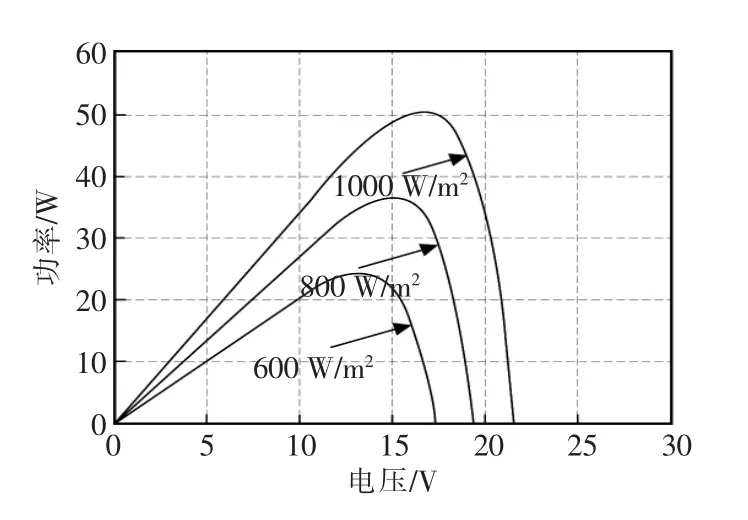
图3 温度恒定(25℃)不同光照强度下V-P曲线Fig.3 V-P curve at different light intensities with constant temperature(25℃)
由图可见,当温度升高时,光伏电池输出功率略微减小;而当光照强度增加时,输出功率增加较为明显。因此,温度、光照强度等外界环境参数对光伏电池的输出功率有较大影响。
2 滑模变结构控制MPPT
2.1 MPPT的控制电路设计
当今DC-DC变换器广泛应用于光伏发电控制系统。它连接于光伏阵列和负载之间,通过控制变换器开关器件的通断使负载与光伏组件的内阻达到功率匹配,从而达到使光伏电池始终工作在最大功率点附近的目的。由于Boost变换器具有较高的能量转换效率,故在此采用Boost升压转换器。由于光伏电池输出电压较不稳定,故在其输出端并入一个稳压电容。其电路拓扑如图4所示。
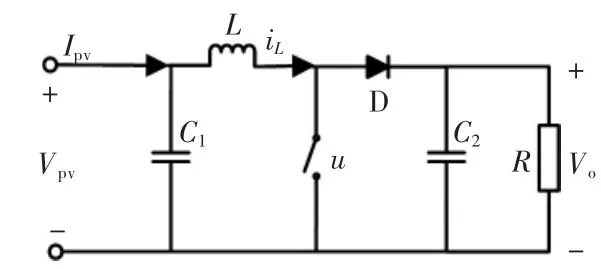
图4 BOOST电路拓扑Fig.4 BOOST circuit topology
图中,Vpv为光伏电池输出电压即Boost电路的输入电压;Vo为Boost电路的输出电压;iL为电感电流。由于电容C1的值较小,故假设iL=Ipv。由图4所示电路拓扑,根据开关器件的导通(u=1)或关断(u=0),经过分析电路可以得到Boost电路的状态空间方程为
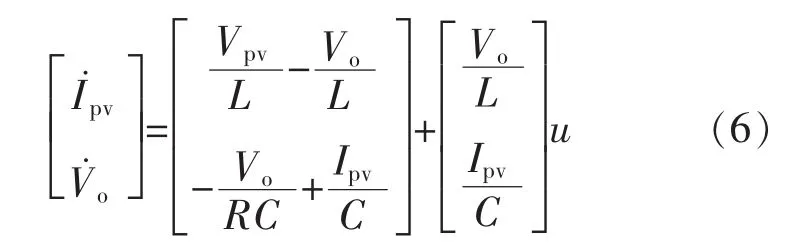
其一般形式为
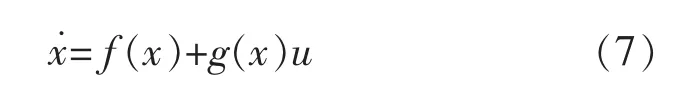
其中
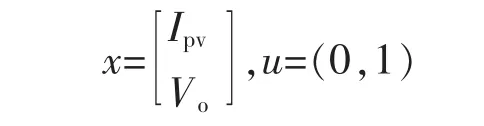
2.2 滑模控制器设计
由图3所示的光伏特性曲线,可以看出光伏电池工作在最大功率点处时,有

即
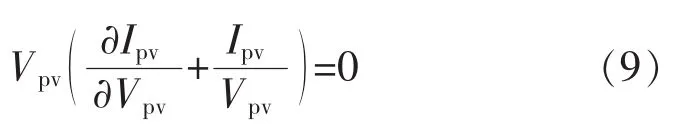
于是,可以选择切换面为[3]
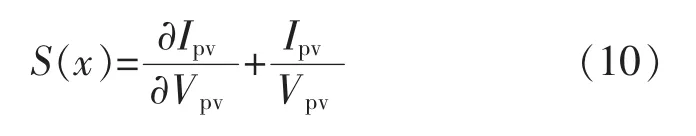
当系统工作在滑模面S˙=0上时,可以用等效控制ueq代替控制函数。由式(10)可得
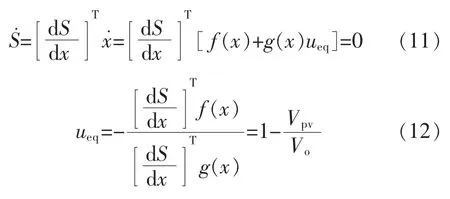
式(7)中的u可以分解为

其中
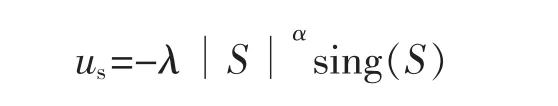
称为幂次趋近率,有利于提高MPPT的快速性,其相关参数设置为 λ>0,α>0。
选取Lyapunov函数:

可得
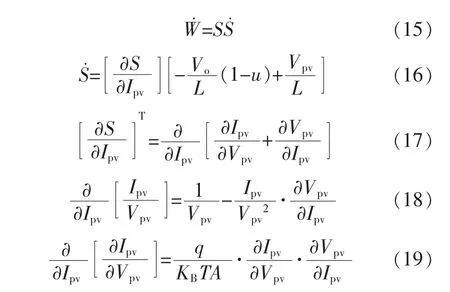
由式(18)、式(19),可得:
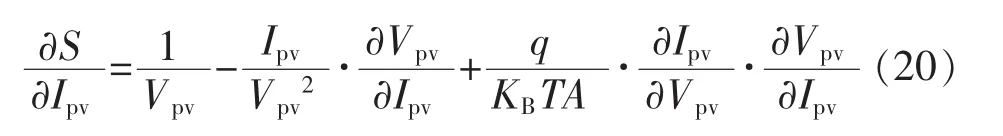
其中
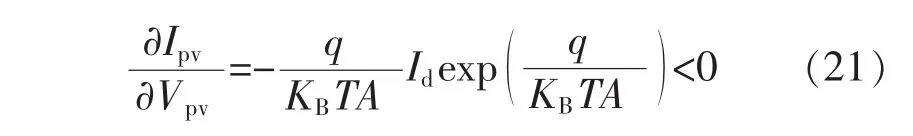
由文献[4],光伏电池输出电压Vpv可以写为
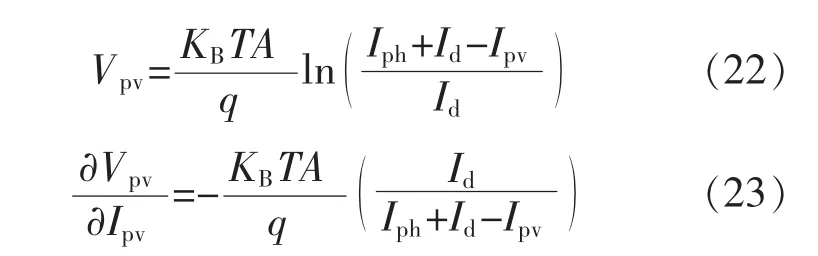
由式(21)~式(23),可以看出:

易知:
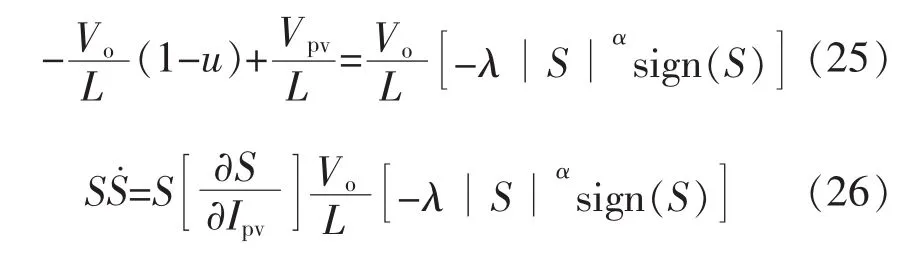
由式(26)不难看出,和符号始终相反,因此滑模切换面函数满足稳定性及可达性[5],滑模控制器的设计符合要求。
3 扰动观察P&O法
扰动观察法,又称爬山法[6],是目前工程实践中最常用的MPPT控制算法之一。当光伏系统开始运行时,系统不断检测光伏电池的输出电压Vpv和输出电流Ipv,计算出功率P(n)。同时,对输出电压施加一定的扰动,并将此刻功率与前一时刻的功率值P(n-1)进行比较。若功率增加,则扰动方向正确,可朝同一方向继续施加扰动;反之,若功率值减少,则扰动方向错误,则应朝着相反方向施加扰动。扰动观察法主要的优点使原理简单,工程中易于实现,但是扰动步长的选择难以确定,若步长较小,跟踪时间会增加,若步长选取过大,会使系统产生较大振荡,造成能量损失严重[7]。
4 仿真试验结果分析
采用MatLab/Simulink软件搭建仿真模型,其中取 Voc=22.4 V,Vm=18 V,Isc=3.5 A,Im=2.9 A,由光伏特性曲线此时输出功率为50 W。在趋近率中取 λ=0.2,α=0.08,C1=C2=100 μF,L=500 mH,经过反复试验,文中采用扰动观察法时选取步为0.01。为避免因滑模控制器输出的控制信号u的频率不稳定而产生抖振现象,在搭建仿真试验模型时,采用将控制信号u与频率为10 kHz的三角波进行调制。运行仿真模型,得到的仿真结果如图5所示。
由图5(a)可见,所选滑模切换面函数 S(x)的值近似于一条恒为0的光滑直线,因此,所设计的滑模控制器满足控制要求,并且在跟踪到最大功率点时由于切换面较光滑故系统振荡较小。由图5(b)可见,由于采用将控制信号u与固定频率的三角波进行比较保证了控制信号u的稳定。由图5(c)可见,负载两端的电压较为稳定,波动较小。由图5(d)可见,采用滑模控制法的跟踪时长比传统P&Q法的跟踪时长缩短了0.06 s,滑模控制跟踪到的功率为48.3 W,扰动观察法则为47.6 W,且滑模控制下的输出功率波动较小。
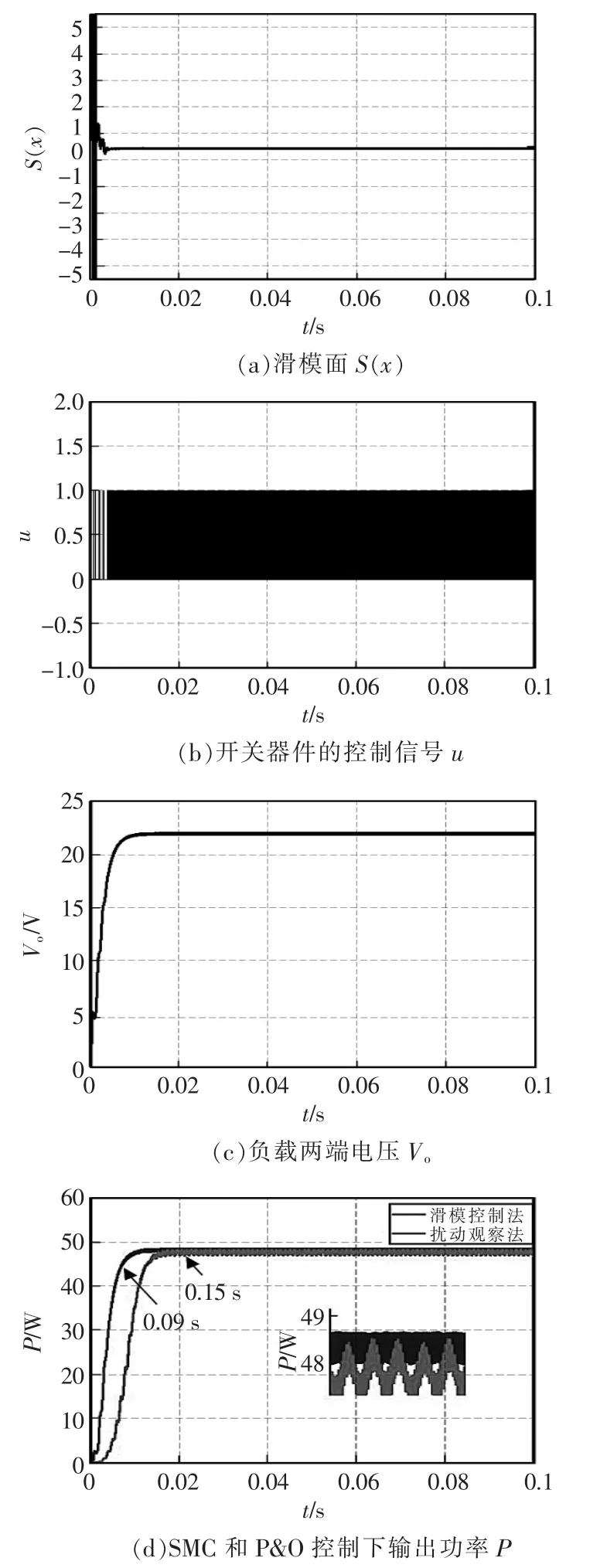
图5 MPPT控制仿真结果Fig.5 MPPT control simulation results
5 结语
针对传统MPPT控制方法上存在的跟踪时间长,系统稳定时存有较大振荡等缺点,提出了基于滑模变结构控制的MPPT算法,设计出相应的滑模控制器,并在MatLab中搭建仿真模型。仿真结果表明,基于滑模控制的MPPT算法比传统的扰动观察法,不仅能够有效的缩短最大功率的跟踪时间,而且能够减小系统在最大功率点处的振荡,使能量得到更高效的利用。

