一类蚜虫种群突变模型的建立与实证分析

那 颖,赵立纯,刘敬娜

(1.辽宁师范大学 数学学院,辽宁 大连 116029;2.鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

突变理论在生态学中的应用已覆盖7种突变模型中的5种,其中,尖角突变模型的应用最为广泛.如赵惠燕研究了以蚜虫为主要控制对象的麦田生态系统,发现麦蚜突变形成危害的过程符合尖角突变模型及其性质,从而用突变理论对麦蚜造成危害的现象给予科学的解释与分析[1];她们还提出棉花苗蚜是棉花苗期的主要害虫,每年都有发生,且受气候、天敌等多因素影响,由于用传统方法很难完全描述和预测,所以利用尖角突变模型解释和预测上述现象[2].这为突变理论在蚜虫种群爆发的深入研究奠定了基础.

回归分析方法在生态系统中的应用也十分广泛.王秀美等人针对小麦蚜虫预测预警准确率不高的问题,使用局部支持向量回归分析构建预测模型,并对未知样本进行预测[3].王向阳等根据小麦蚜虫及其天敌的调查数据,采用逐步回归分析,筛选出相关性强的预报因子,建立中长期预测模型并给出预测结论[4].田洁基于实验数据,利用回归分析方法,建立拟合度较高的尖角突变模型,刻画蚜虫种群的生长情况[5].这些研究的应用均为多元线性回归,而多元非线性回归在突变理论中的成果较少见.

本文结合突变理论和回归分析方法,分析数据的突变特征并判别控制变量类型,建立尖角突变模型.再利用R2值和F′统计量,以线性模型和Logistic模型为参考,分析所建模型的拟合度.最后,根据突变理论对模型的平衡点和稳定性进行分析,结果可为蚜虫种群的预测预报提供参考.

1 模型建立

1.1 数据处理

为使所描述的模型更符合实际,以西北农林科技大学某年蚜虫种群生态系统调查资料为基础数据,其中，包括百株蚜量、天敌量和以月、旬或候为一个时段单位的平均气温、平均相对湿度、平均降水、平均日照时数.

根据蚜虫种群生态系统的调查资料,百株蚜量的数据很全面,所以把蚜虫种群作为本文研究的状态变量,记为x;由于蜘蛛量的数据也很全面,所以把蜘蛛量作为与天敌种群相关的控制变量,记为a;而另一个控制变量是复合平均气温、平均相对湿度、平均降水、平均日照时数的一个复合的气象因素,记为b.利用主成分分析法,得到主成分得分和各个主成分贡献率的结果如下：

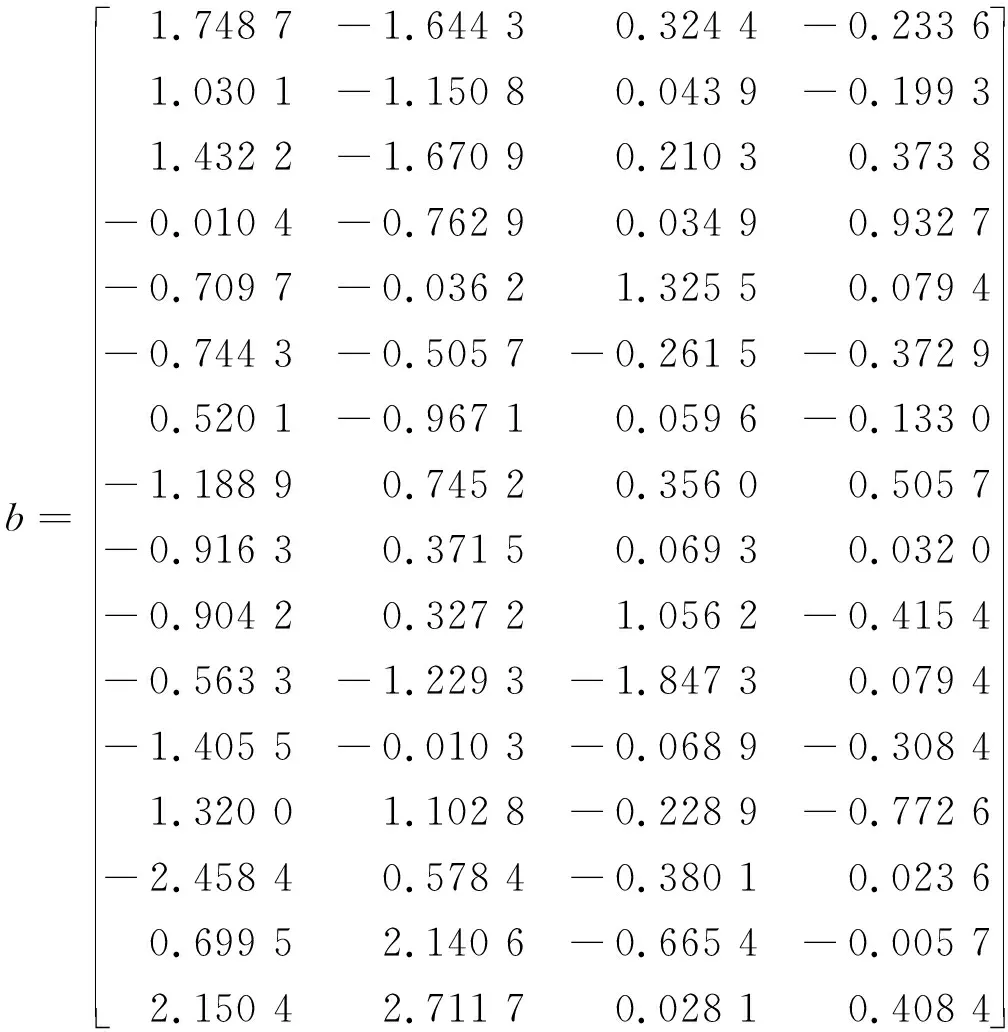
其中，矩阵的第一列代表b1的主成分得分,第二列代表b2的主成分得分,第三列代表b3的主成分得分,第四列代表b4的主成分得分.

b1的贡献率为42.935 5%,b2的贡献率为40.653 9%,b3的贡献率为12.144 4%,b4的贡献率为4.266 2%.

根据b1,b2,b3和b4的主成分得分,并用其贡献率加权,得到基于气象因素的复合控制变量b的表达式为:

b=42.935 5%b1+40.653 9%b2+12.144 4%b3+4.266 2%b4,

其中,b1代表平均气温,b2代表平均相对湿度,b3代表平均降水,b4代表平均日照时数.

注:由于控制变量b能够较好地反映气象因素的变化信息,因此本文中气象因素可以看成蚜虫种群发展变化的主导因素之一.

1.2 突变特征分析

考虑到以往研究从理论上说明突变特征问题的主观盲目性[6-7],本文基于实际数据,绘制状态变量分别随两个控制变量变化的散点图(见图1),来判断蚜虫种群的突变特征.

图1 蚜虫种群生态系统散点图

由文献[8]得到,当控制变量连续变化时,如果状态变量有不连续的跳跃行为,则说明蚜虫种群具有突变特征.

图1中存在5个不连续行为,其中1是由于控制变量a突然变化引起的不连续行为,所以1不是突变现象;2是由于控制变量a和控制变量b突然变化引起的不连续行为,所以2不是突变现象;3是由于控制变量a和控制变量b渐变引起的不连续行为,所以3是突变现象;4是由于控制变量a和控制变量b突然变化引起的不连续行为,所以4不是突变现象;5是由于控制变量a和控制变量b渐变引起的不连续行为,所以5是突变现象.

综上可知蚜虫种群具有突变特征,由于这个突变特征是由两个控制变量a和b连续变化引起的,所以可以考虑用尖角突变模型来刻画蚜虫种群的突变现象.但哪个变量对模型突变起主要作用,需要进一步思考.

1.3 控制变量类型判别

文献[9]提出,尖角突变模型的一般形式为:

x3+ux+v=0,

(1)

其中,x代表尖角突变模型的状态变量,u代表剖分变量,v代表正则变量.

为了准确判别正则变量和剖分变量,假设u=a和v=b,得到如下模型:

x3+ax+b=0,

(2)

或者相反,假设u=b和v=a,得到如下模型:

x3+bx+a=0.

(3)

再借助SPSS软件,分别对尖角突变模型(2)和(3)进行多元非线性回归分析,得到结果如下:

SSResidualcusp1=7.397,R2cusp1=0.171,

SSResidualcusp2=138.364,R2cusp2=0.166.

由于R2cusp1>R2cusp2且SSResidualcusp1

(4)

2 拟合度分析

Malthusian线性模型[11]和Logistic模型[12]在刻画种群增长方面应用极其广泛,用本文提出的尖角突变模型与线性模型和Logistic模型对比,来分析拟合度更具有说服力.下面基于实际数据分析3个模型的拟合度,具体分析如下:

根据实测资料,许多生物和环境研究量没有负值,例如天敌和气象因素,因此,需要将原来的坐标系进行坐标变换,将原来的a,b轴平移和旋转,使之具有生物意义.这样将模型(4)平移旋转后得:

p1xi+q13+p2ai+q2xi+q1+bi+q3=0.

(5)

根据Malthusian模型,在其它条件最优时,天敌种群数量a的变化直接影响蚜虫种群的变化率,而气象因素对蚜虫种群的影响具有一个最优值取为ε,基于此,得到如下模型:

(6)

将模型(6)平移旋转后得:

p1xi+q1ai+q2-|b+q3-ε|=0，

(7)

对模型(7)进行回归分析,得到结果如下:

SSResidualplane=8.920,R2plane=0.082.

根据模型Logistic,一般状态下,蜘蛛量a是与内禀增长率r相关的变量,气象因素b是与环境容纳量K相关的变量,得到如下模型:

，

(8)

将模型(8)平移旋转后得:

(9)

对模型(9)进行回归分析,得到结果如下:

SSResidualLogistic=603.783,R2Logistic=0.161.

上述ai,bi,xi(i=1,2,…,16)是实测数据，qi(i=1,2,3)为平移的距离,pj(j=1,2)为旋转的角度.

从得到的R2值和SSR可知,尖角突变模型的拟合度最优.为进一步验证,根据显著性检验[8,13],设F′统计量如下:

(10)

其中，n表示样本总数,在本文中n=16.若F′>0,说明SSResidualplane>SSResidualcusp,意味着尖角突变模型拟合度优于线性模型;同理若F′<0,说明SSResidualplane

(11)

显然F1′=1.132>0,说明尖角突变模型拟合度优于线性模型.同理构造Logistic模型和尖角突变模型的统计量F2′,通过计算F2′=0.287>0,说明尖角突变模型拟合度优于Logistic模型.

3 模型分析

考虑尖角突变模型(4)，把由x′(t)=0确定的曲面称为平衡曲面，即

x3+ax+b=0.

(12)

把x′(t)=0与x″(t)=3x2+a=0联立消去x，可得到控制空间中的方程

4a3+27b2=0,

(13)

式(13)所确定的曲线称为分歧点集.

方程(12)是一个3次方程，它或是有1个实根，或者有3个实根，实根数目由判别式Δ=4a3+27b2决定.如果Δ≤0，则有3个实根；否则只有1个实根.

Δ=0时，或者两个实根相同a,b≠0，或者3个根全都相同a=b=0.

这说明当Δ<0时，x(t)有两个极小值，一个极大值，即两个平衡点.Δ>0时，x(t)只有一个平衡点.

利用卡尔丹诺公式求解x3+ax+b=0得：

图2 尖角突变分区仿真图

根据各平衡点的Jacobi矩阵,可得Dxfxi,a,b=3xi2+ai=1,2,3，根据Dxfxi,a,b的符号判断，当3xi2+a<0时，平衡点稳定；当3xi2+a>0时，平衡点不稳定.

利用Matlab绘制尖角突变分区仿真图(见图2).

由图2可以看出:当Δ<0时,满足条件的控制变量a,b值位于尖角区域内,处于潜在危害区,这是一不稳定区域,随时可向两极发展;当Δ>0时,a,b值所决定的点落在尖角区域外,分别为稳定安全区和稳定危害区,其中,凡是控制变量(a,b)控制的点落在稳定安全区内,它们都处于尖角区域的左侧;当Δ=0时,a=b,则x=0,这时对应的正是尖角的地方.如果平衡点位于潜在危害区,这表明蚜虫种群可能发生突变,此时可采用生物防治的办法抑制蚜虫种群爆发;如果平衡点位于稳定安全区,这表明该时间段蚜虫种群没有威胁到小麦生长,此时可做常规防治工作;如果平衡点位于稳定危害区,这表明蚜虫种群处于大爆发期,已经严重危害小麦生长,此时应及时进行化学防治.