六自由度钻杆装卸机械手运动学研究

陈光柱，邓 熠，邱士安 ，付 林

（1.成都理工大学核技术与自动化工程学院，四川 成都 610059；2.成都工业学院材料工程学院，四川 成都 611730）

1 引言

工程钻机机器人是一种主要应用于建筑工程施工、地质勘探、煤矿开采等领域的工程钻探设备，其具有自动化程度高，生产作业快速，支护能力强等特点。工程钻机机器人的使用大幅度提高了工程行业的施工效率，同时让工人从恶劣的工作环境和繁重的工作作业中解放出来，极大地降低了钻进过程中的操作危险性[1]。钻杆装卸是钻机机器人极为重要的工作环节，该环节的效率高低直接影响整机的工作效率，故国内外学者针对钻杆自动装卸技术开展了大量研究，并且在实际生产中取得了许多应用成果。在20世纪初，国外Williamson公司的Rovdrill钻机、澳大利亚PROD钻机、德国不莱梅MeBo钻机安装了钻机钻杆自动存取系统，极大地提高了工作效率[2-4]。1999年，宝鸡石油机械厂在研制的GWM1000钻机上首先开展关于钻杆自动拆卸技术与系统的研究。2001年，兰州石油化工机器厂生产的陆地沙漠钻机采用了钻杆存取系统。2010年，烟台中集公司在深水半潜式钻井平台，配备国外的钻杆自动存取装置，实现了全自动化钻进和起下钻具等功能。2011年，我国首次自助设计的“海洋石油981”上配备HR柱形存取系统以及钻杆移送装置。2014年，某科技大学机电工程学院进行了液压钻车钻杆自动装卸装置的设计[5-7]。

可以看出，目前钻杆自动装卸系统及技术在钻井平台上已经得到了较为广泛的应用。然而，由于工作环境的特殊性及复杂性，目前工程钻机的钻杆装卸还未实现自动化，仍采用手动换接方式，其不但工作效率低下，而且安全隐患大。鉴于此，设计一种六自由度钻杆装卸机械手，以实现工程钻机钻杆的自动换接。在此基础上，建立机械手的运动学模型，并进行仿真研究。

2 钻杆拆卸机械手运动学方程建立

2.1 三维模型建立

设计的六自由度钻杆装卸机械手，如图1所示。主要由基座、钻杆抓取器和五个通过R副和P副实现连接的连杆组成。机械手腰部、机械手大臂、机械手中臂、机械手小臂之间的关节运动方式为旋转运动，具有3个自由度，机械手腰部自身带旋转功能，具有1个自由度，而旋转移动部件能实现转动和移动，具有2个自由度，故机械手总共拥有6个自由度。钻杆抓取器在各关节液压马达的驱动下，按照预定的路径将钻杆送至钻机或者将钻杆从钻机中取出放入钻杆库。由于该机械手自由度数较多，相对来说具有更加开阔的工作坏境。因此，钻杆抓取器能够运动至空间中任意位置，具有较高的灵敏度，同时也易于实现避障。

图1 六自由度钻杆装卸机械手Fig.1 Six DOF Drill Pipe Handing Manipulator

2.2 钻杆拆卸机械手运动学模型建立

对六自由度钻杆装卸机械手进行运动学研究是机械手设计一个重要步骤。当已知机械手所有关节变量时，求出机械手的运动学方程，就能描述出钻杆抓取器在空间中的准确位姿，此为运动学正解。在钻杆抓取器特定的位姿下对机械手的运动学方程求解，得出钻杆抓取器在此位姿下的关节变量，此为运动学逆解。之后可以进一步得出机械手每个运动构件的速度，加速度，关节变量等参数，能够为机械手的动态性能优化，结构参数优化，整机控制等后续研究工作提供理论基础和参考依据。Denavit和Hartenberg在1955年提出一种D-H连杆坐标变化法，这种方法在机器人设计领域内得到了广泛的应用[8]。建立六自由度钻杆装卸机械手D-H坐标系，如图2所示。建立D-H参数，如表1所示。

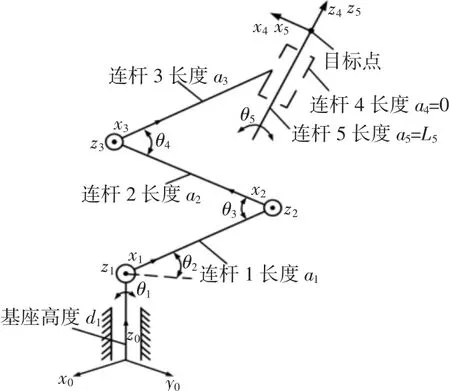
图2 六自由度钻杆装卸机械手D-H坐标系Fig.2 Six DOF Drill Pipe Handing Manipulator D-H Coordinate

表1 六自由度钻杆装卸机械手D-H参数Tab.1 Six DOF Drill Pipe Handing Manipulator D-H CoordinateParameters

根据表1中的参数，机械手各个连杆D-H坐标变化矩阵为：

将上述六个矩阵相乘得到机械手的运动学方程为：

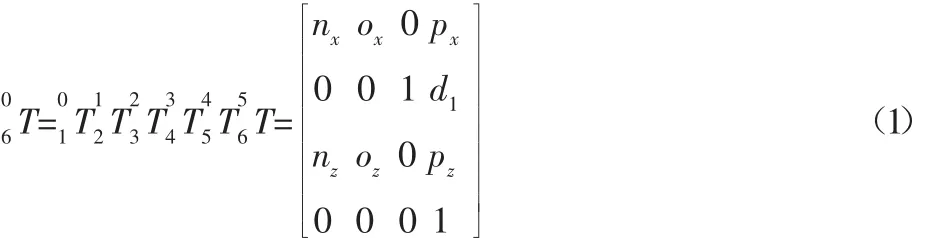
如果已知每一个关节变量θn，将其代入式（1）就得出可以机械手在空间中的确定位姿。

3 机械手运动学逆解求解

3.1 遗传算法介绍

工程钻机机器人在钻进过程中，钻杆装卸机械手需要根据钻机主轴孔的位置确定各关节变量值，然后驱动各关节运动，完成钻杆的抓取、移动、放置等动作，这实际上是对钻杆装卸机械手进行逆运动学分析。遗传算法通过模仿自然界中选择与遗传的机理寻找最优解。算法求解过程中引入选择、交叉和变异三个遗传算子作为核心操作步骤，采用概率的变迁规则指导目标函数进行求解。通过引入概率的搜索方法，整个算法的搜索过程始终朝着搜索空间更优化的解区域移动[9-10]。在评价基因个体时采用适应度函数对其进行评价，不需要外界辅助信息，也不容易陷入局部最优解，是一种全局范围内的最优搜索算法。

3.2 算法设计

3.2.1 目标函数设计

将钻杆与钻杆安装孔间的装配关系视为一个孔轴配合从而可以利用孔轴配合的同心度误差对钻杆与钻杆安装孔间的相对位置关系进行评价。钻杆与钻杆安装孔间允许的最大同心度误差可用下式计算：

式中：p—同心度误差；s1—孔的基准尺寸，此处为钻杆安装孔的直径；s2—配合轴的最大尺寸，此处为钻杆直径。

设s1=45mm，s2=42mm，由式（2）计算出钻杆与钻杆安装孔间允许的最大同心度误差pmax=0.9mm。为使钻杆抓取器运动到预定位置且满足最大同心度误差要求，可将钻杆与安装孔间的同心度误差的几何关系表达式作为遗传算法的目标函数，定义如下：

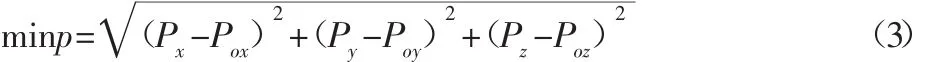
式中：Px，Py，Pz—钻杆抓取器中心位置坐标；Pox，Poy，Poz—主轴孔指定点位置坐标。从式（1）的参数解释中可以看出Px，Py，Pz与关节变量θ2，θ3，θ4成互相耦合的关系。因此将三个关节变量θ2=［40°，50°］、θ3=［55°，60°］、θ4=［90°，100°］作为约束条件。对式（3）求解可以得出能够使钻杆抓取器到达指定位置的关节变量。

3.2.2 算法过程

采用二进制编码，将解的精度设定为0.001。关节变量θ2、θ3、θ4的编码长度分别为 n1，n2，n3。n1=log2［（50-40）/0.001+1］=14，n2=log2［（60-55）/0.001+1］=13，n3=log2［（100-90）/0.001+1］=14。则总的编码长度为n1+n2+n3=41。

算法通过下述几个步骤完成：（1）初始化种群。随机生成50*41的矩阵，即个体数目为50，个体长度为41。（2）确定选择算子。选择出符合条件的父体。（3）确定交叉算子。设置交叉概率Pc为0.8，通过上一个选择步骤得出的所有父体进行两两随机配对并进行交叉，得到新的个体。（4）确定变异算子。将变异概率Pm设定为0.01，使上一步骤产生的新个体进行变异，再一次产生新的个体。（5）如果步骤（4）产生的新的个体数达到50，则形成一个新群体；否则，返回步骤（2），再次运行算法程序。

在图2中，各连杆长度分别为a1=227.62mm，a2=363.10mm，a3=340mm，d1=55mm，L5=380.47mm，钻杆需要到达的点坐标为（-578.08mm，0，755.62mm）。种群规模取 50，交叉概率取 0.8，变异概率取0.01。由于机械手参数θ1和θ5的值取决于钻机的工作角度，将这两个角度脱离机械手的控制，由钻机的控制程序进行控制。因此θ1，θ5和相关参数d1=55mm不纳入算法程序中，利用遗传算法进行运动学逆解求解，运行十次得到结果，如表2所示。

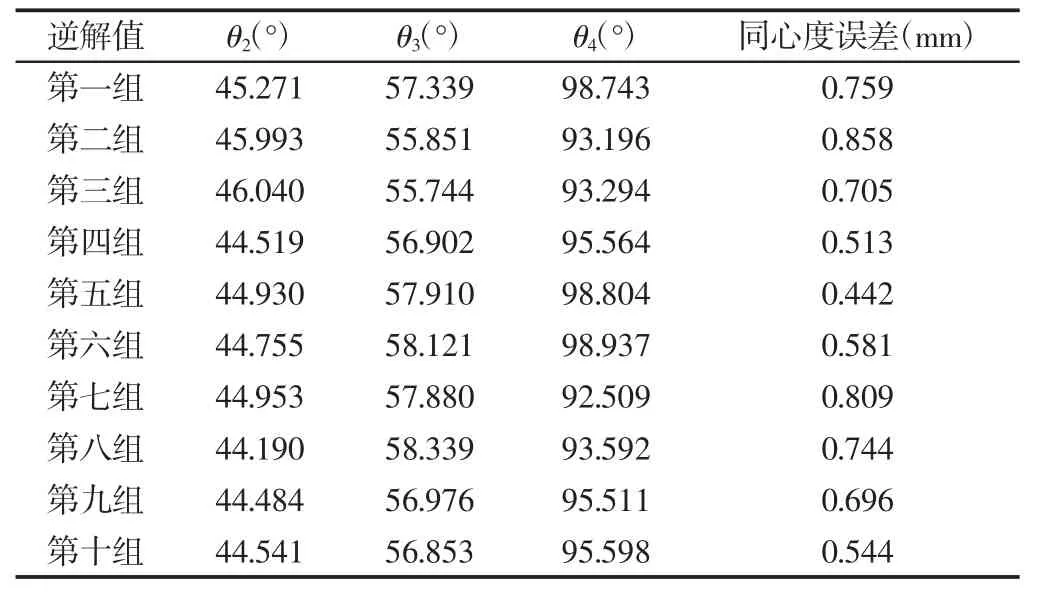
表2 求解的关节变量值Tab.2 The Solved Joint Variable Value

由于遗传算法具有一定的随机性，因此表2中的十组解有一定的差异。但是可以看出，每一组解的同心度误差均小于标限定值0.9，均符合设计要求。这同时也表明了遗传算法在处理该类数学问题时具有较高的稳定性。取同心度误差最小的一组解（第五组解）作为此次逆解求解的最优解，以作为后续控制参数。

4 机械手运动学仿真分析

为使机械手的运动过程直观化，对采用遗传算法求出的逆解进行检测，将机械手几何模型导入UG软件运动学仿真模块中进行运动学仿真，采用点到点运动轨迹规划，取机械手中每个连杆的质心为跟踪点，设置运动时间为160s，第5s到110s内为各连杆绕自身关节转动，110s到140s内为抓取器通过移动，将钻杆送上钻机[11]。将2.2节求出的最优解作为机械手的关节输入量，通过UG软件运动学模块进行位置仿真。通过观察仿真结果，得出钻杆抓取器停止时的中心点位置坐标为（-578.08mm，0，756.07mm）。将其带入式（3）中进行计算，得出同心度误差为p1=0.45mm，而遗传算法计算出的同心度误差p2=0.442mm，说明通过遗传算法求出的逆解可以使得钻杆抓取器到达指定位置，且同心度误差较小。同时该逆解值可以作为机器人后续控制研究工作的理论研究依据。

进一步设定两种驱动方式，一种为机械手所有关节依次运动，另一种为机械手所有关节同步运动。将逆解分别作为两种驱动方式的输入源进行仿真，得出两种驱动方式下的运动参数曲线，如图3、图4所示。

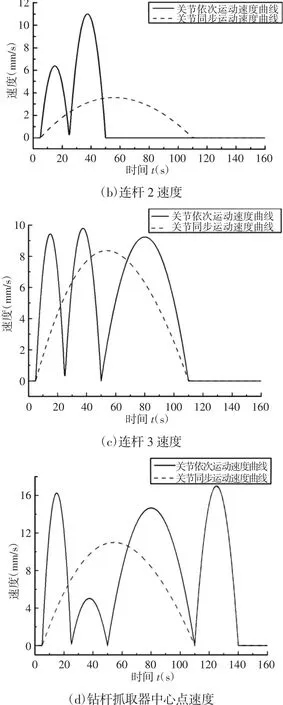
图3 各运动部件质心速度Fig.3 Centroid Velocity of Moving Parts

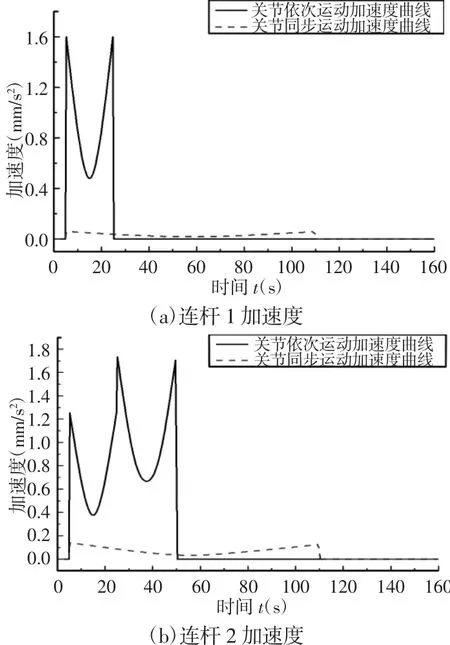
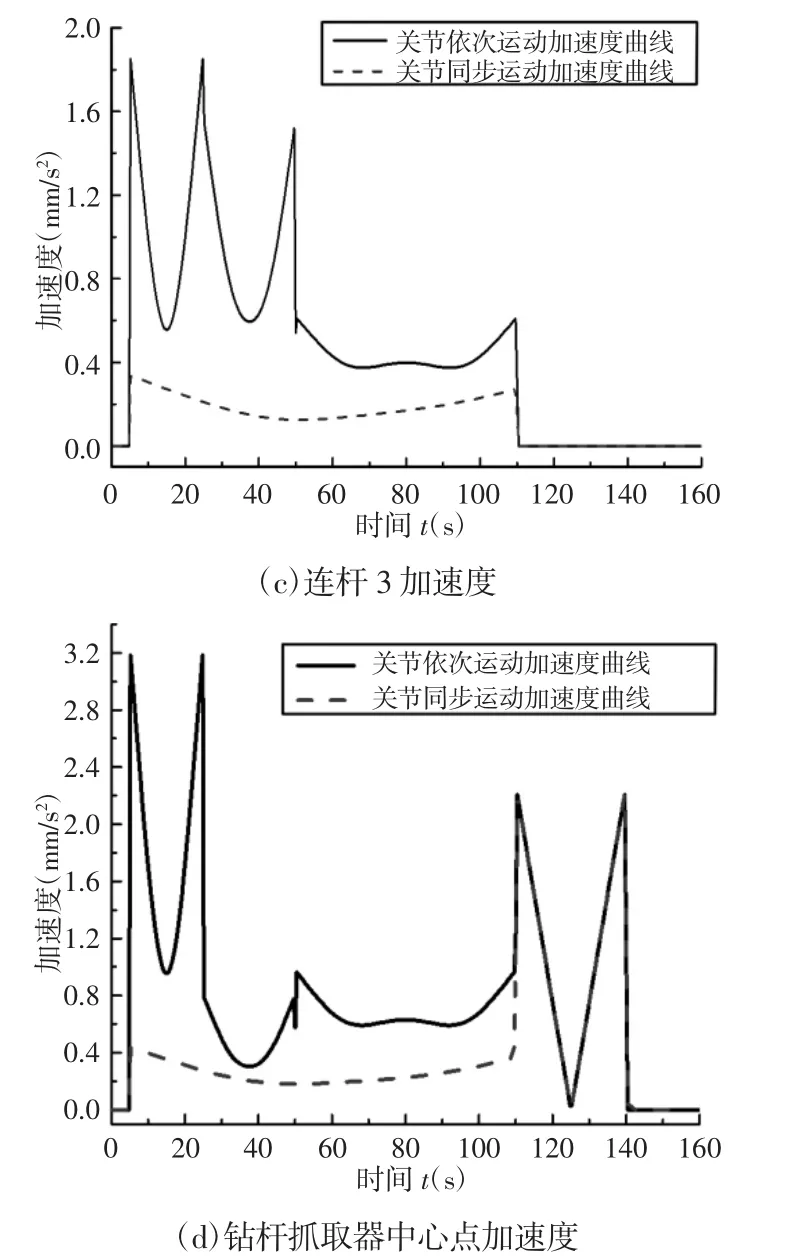
图4 各运动部件质心速度Fig.4 Centroid Acceleration of Moving Parts

图 3 和图 4 每幅图中的（a）（b）（c）（d）描述了机械手各个连杆和钻杆抓取器质心的运动状态。而每幅图中的（d）最后一部分加速度曲线线形发生了变化，是因为在第110s时钻杆抓取器的运动方式发生了改变。经过对比可以看出在相同的时间段内，采用关节依次运动驱动方式时，各个运动部件的速度与加速度呈现叠加状态，加速度的数值整体偏高。驱动方式下连杆1的加速度最大值为1.6mm/s2，连杆2加速度最大值为1.78mm/s2，连杆3加速度最大值为1.93mm/s2，钻杆抓取器加速度最大值为3.2mm/s2。而当采用关节同步运动驱动方式时，所有的连杆和钻杆抓取器的最大加速度值不到0.5mm/s2。由加速度曲线线形可以看出，采用关节依次运动驱动方式时，曲线变化极为不平滑，整机在运动过程中有可能因为构件加速度突变次数较多而显得运动不稳定。同时加之外界工况和振动的影响会使得整机结构的动态稳定性较差，长期下去会严重影响设备零部件的刚性和整机结构的稳定性，最终导致设备提前损坏。相比之下，采用关节同步运动驱动方式时，速度和加速度曲线变化平稳，且加速度数值较小（所有的连杆和钻杆抓取器的最高加速度不到0.5mm/s2），同时加速度线形平滑且数值分布均匀，故机械手的整个运动过程将更为平稳。从图4的加速度曲线对比中还可以看出，采用关节同步运动驱动方式时，工作时间段内加速度的突变次数远低于采用关节依次运动驱动方式时的加速度突变次数，这意味着在同等的工作时间段内，关节所受到的刚性冲击较小，其不会因自身运动冲击频繁而过早发生坏损。综上分析可知，采用关节同步运动驱动方式时，机械手的运动状态相对较好。

5 结论

（1）结合工程钻机机器人的结构和工况条件，设计了一种拥有5个转动关节和1个移动关节的六自由度全液压驱动钻杆装卸机械手，实现了钻机钻杆装卸的自动化，提高了钻机的总体工作效率。

（2）采用D-H方法建立了六自由度钻杆装卸机械手的运动学方程，以钻杆与钻杆安装孔间的同心度误差作为目标函数，利用遗传算法对运动学方程进行了逆解求解。进一步将逆解作为输入参数，在UG软件中对机械手的运动学进行了仿真分析，仿真所得机械手钻杆抓取器器中心点位移曲线规律验证了运动学方程的正确性和算法设计的合理性，为机械手的控制研究提供了理论基础。

（3）提出了同步运动和依次运动两种机械手关节驱动方案，对两种方案下钻杆装卸机械手的运动学过程进行了仿真分析，通过对比分析表明，同步运动方式可使钻杆装卸机械手获得较好的速度和加速度性能，优于依次运动方式，为关节驱动方式的选取提供了依据。