考虑样本特征的第三方物流安全库存预测模型

夏 田，邓 萌

（陕西科技大学 机电工程学院，陕西 西安 710021）

1 引言

汽车制造业第三方物流安全库存作为保证制造生产而储备的库存量，不仅影响第三方物流投入成本、物流成本和企业效益，而且保障着整个汽车供应链的高效与顺畅运行，因此对其进行合理预测和设置尤为必要。而在汽车供应链中，参与主体多、地域范围广、中间环节多、信息流通复杂、行业要求高等特征，使安全库存的预测受多种非线性相关因素影响，增加了汽车制造业第三方物流安全库存预测难度。

目前，对安全库存的预测主要分为两类方法，第一类通常采用统计方法，通过对安全库存历史数据的分析、以及从业者的经验判断进行安全库存的预测，其人为干扰性强，安全库存客观参量的选取没有统一标准，预测误差较大，不利于推广运用；第二类方法通过建立各种模型进行安全库存的预测，大大增加了预测的准确性和科学性，减少了人为干扰性，运用算法主要包括BP神经网络算法、混沌神经网络算法等[1]，较少使用支持向量机算法，其中模型输入参量数量多、重复性高，缺少对制造商与仓库属性的描述参量，且仅限于安全库存数据的预测，缺少对影响安全库存客观参量的定量研究。针对现有模型中神经网络算法易受网络结构和样本复杂性影响、描述参量不全面、不适用于成立期或发展期的第三方物流等问题，同时针对准确度以及实际使用价值方面，提出一种运用最小二乘支持向量机（Support Vector Machine，SVM）算法的第三方物流安全库存预测与参量权重计算相结合的闭环双向模型。该模型不但充分利用了支持向量机小样本预测的优势，而且基于供应链整体性和连续性的考虑，选取供应商属性、物料属性、制造商属性和仓库属性作为输入层客观参量，提高了预测准确率和效率。并通过对预测结果中支持向量的分析，得出各特征变量权重计算模型，可准确预测安全库存量，并为安全库存的准确设置和供应链系统改善提供了理论依据。

2 研究方法

（1）最小二乘支持向量机

最小二乘法支持向量机（LS-SVM）的原则是以“残差平方和最小”确定直线位置，得到的估计量还具有优良特性，对异常值具有高敏感性[2]。

给定训练数据的N个样本可以表示为｛xk，yk｝，其中输入数据xk∈Rm，输出数据yk∈R，支持向量机的最优化问题可表示为：

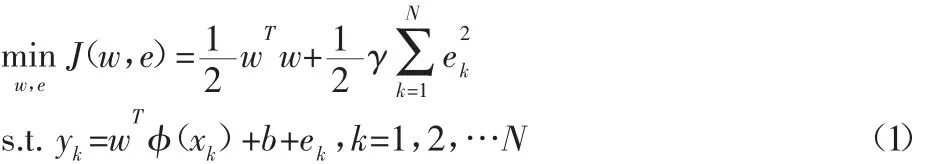
对于非线性的情况，SVM通过核函数进行处理，其拟合模型为：

式中：αk—支持向量；K（xi，xj）—核函数。

（2）Grid-Search_PSO优化SVM参数原理

选用Grid-Search_PSO来优化SVM参数，通过不断迭代求解优化参数问题，实现以较快的速度收敛并找到全局最优解[3]。

（3）输入层参数权重分析模型

SVM输出网络对第m个特征输入向量的相关度可对其进行偏导数计算求得近似解：

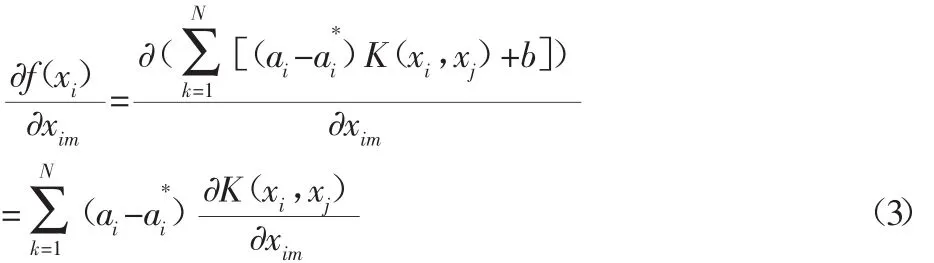
式中：M—输入向量的维度数目；N—训练所得支持向量数目。

特征向量权重计算公式[4]为：

式中：T—训练样本个数。

3 汽车制造企业第三方物流安全库存预测模型建立

LS-SVM第三方物流安全库存预测模型，如图1所示。该模型利用SVM建立的回归模型对第三方物流仓库安全库存进行预测，解决了神经网络算法存在的过学习和局部最小值问题[5]，能够快速处理高维度复杂数据，所需样本数目也大大减少[6]。其具体步骤如下：

（1）输入输出层的设置

通过影响安全库存的各客观参量对安全库存进行预测并对各客观参量权重进行计算，因此确定各客观参量为输入层，安全库存和客观参量权重为输出量。

（2）客观参量的选取

从汽车供应链的角度对客观参量的选取进行全面化整体化考虑。现有模型的输入参数缺乏对完整汽车供应链中第三方物流自身属性的描述，预测所得安全库存数据与第三方物流实际仓储情况存在较大误差[7]。因此，本模型在建立过程中从汽车供应链角度入手，将第三方物流特征参数加入输入层中，除了选取一般安全库存预测模型中供货量、订单延时、次品率、存储成本4个共有输入参数外，还选择了现有库存量和库存需求量2个参数共计6个维度作为模型输入层参数，不仅对参数数量有所精简，而且数据维度更为全面。

（3）核函数的选取

使用回归分类中应用最为广泛、精度较高、计算速度快的RBF核函数为该预测模型拟合核函数。

（4）预测模型参数优化

参数选择主要是寻求回归的最优参数c和g，由SVMcg For Regress.m实现[8]，其接口为：

（5）模型测试、训练和预测

为了提高预测准确率，在数据样本进行筛选和归一化处理过程之后，将其分为训练集和测试集两大类。

（6）客观评价参量权重分析

安全库存输入层各属性参量与安全库存预测数据间相互影响关系复杂，且存在较大随机性及较低的相关性，不能通过精确的数学模型进行客观描述。在建立的LS-SVM安全库存预测模型基础上，将输入参量与输出变量之间的关系进行权重量化研究，得出输入参量影响权重分析理论计算模型。

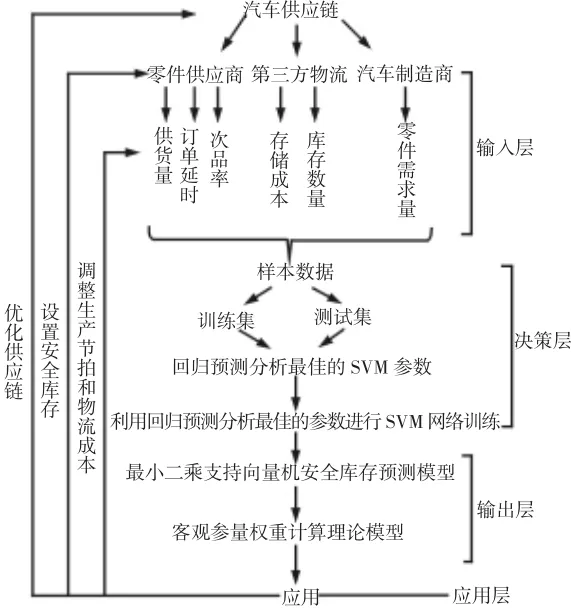
图1 安全库存预测模型Fig.1 Safety Stock Forecasting Model

4 第三方物流安全库存的预测

图2 预测流程图Fig.2 Prediction Flow Chart

某品牌汽车生产中的第三方物流中心负责将各地域零部件供应商按订单供应的零件进行分类存储后按照汽车制造商每日发出的拉动单准时保量进行发货，以其各参量历史数据为例，进行安全库存的预测，具体流程，如图2所示。

（1）预测参数的收集

以第三方物流公司50个周的供货量、订单延时、次品率、存储成本、存货需求量、现有库存共6个参量的历史数据作为预测样本，如表1所示。

表1 原始数据Tab.1 Raw Data

（2）根据模型选定自变量与因变量

安全库存预测模型中以上一周的库存数、供货量、订单延时、次品率、存储成本、存货需求量、订货间隔期作为本周安全库存的自变量，本周的安全库存作为因变量。

（3）输入数据预处理

使用Mapminmax函数来实现，对自变量与因变量集合均进行归一化预处理[9-10]，即 yi∈［1，2］，i=1，2，3…n。该第三方物流公司原始每周的库存数目归一化后的结果，如图3所示。

图3 原始数据归一化后的图像Fig.3 Normalized Image of Raw Data

（4）模型参数寻优

图4 SVR参数选择结果图Fig.4 SVR Parameter Selection Result Diagram

经过Grid-Search_PSO参数寻优过程[11]，最终得到的最优SVM参数惩罚因子C=8，RBF核函数中参数g=2.8284，（g=-1/图 4 所示。

（5）训练回归预测

利用步骤（4）中得到的c和g对SVM进行修正。建模时将经过回归处理的50组数据作为输入，其安全库存量作为输出，取前45组数据作为训练样本集，取（46～50）组数据为预测样本。

初始数据与回归预测结果数据的对比图，如图5所示。从回归预测值和实际值的图像可以发现两者相符程度较为理想。经计算，Squared Correlation Coefficient=0.996734，MSE=0.00045342，R=99.6734%，说明该预测模型学习训练效果较为理想。

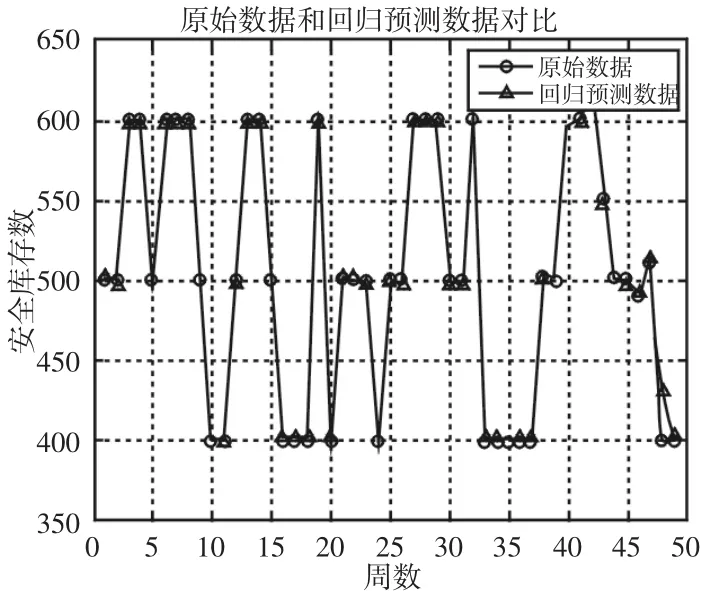
图5 原始数据与回归预测数据对比图Fig.5 Comparison of Raw Data and Regression Forecast Data

（6）输出预测模型

由模型求得变量可知，安全库存预测模型公式为：

式中：wi—支持向量在决策函数中的系数；xi—支持向量；x—带预测样本向量。

（7）输入层参数权重分析

由式（4）可得，安全库存预测模型输入层参数权重计算模型为：

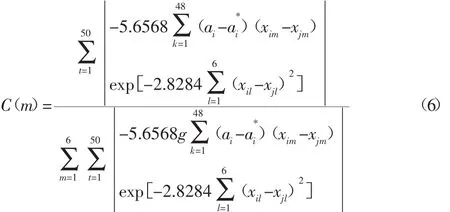
5 结论

模型整体形成闭环结构，由输入层、决策层、输出层、应用层组成，为优化供应链、设置安全库存、调整生产节拍和物流成本提供了理论依据。该模型克服了基于神经网络库存预测模型存在的不足，与其他基于支持向量机的预测模型相比，输入层参数更为全面且加入了第三方物流自身描述属性，提高了预测精确度。通过实例验证，检测了该模型的可行性与科学性。