漂浮基空间机械臂系统的非完整性研究

陈正仓 ，周维佳

（1.中国科学院沈阳自动化研究所 机器人学国家重点实验室，辽宁 沈阳 110016；2.中国科学院大学，北京 100049）

1 引言

随着航空航天工业的不断发展，空间机械臂越来越多地代替或辅助宇航员完成部分或全部的空间任务。目前，空间机械臂系统主要包括固定基空间机械臂系统，自由飞行系统和自由漂浮系统。前两种系统与自由飞行系统的根本区别在于：前者的基体上安装有位姿控制系统。尽管基体位姿控制系统具有较多的优点，但是其缺点也较为明显。其中包括，姿态控制器姿控能力的饱和问题，位置控制器废气影响临近结构运动状态的问题，尤其要提到的是，位姿控制系统会消耗过多的不可再生能源，进而增加空间机械臂系统的制造成本，甚至影响整个太空任务的寿命。因此，漂浮基空间机械臂系统越来越受到科学家们的重视。与固定基机械臂系统（如工业机械臂）不同，漂浮基空间机械臂系统（自由漂浮系统）在运动学、动力学和控制方法方面存在着诸多新的特点[1-2]。

由于没有固定约束，机械臂的运动会导致漂浮基体的位姿发生变化，基体位姿变化又会反过来影响机械臂末端执行器的定位和操作精度。这种内部耦合关系使得机械臂的控制变得更加复杂[3]。

目前，国内外学者在多体系统非完整性分析领域做了很多工作。文献[4]对非完整系统在控制过程中的应用进行了综述。文献[5]对空间机械臂系统目标捕获过程中的零响应操作进行了分析，其中，系统的非完整性是问题出现的最大障碍，同时也是求解问题的关键。文献[6]对具有非完整约束的轮式移动机器人的轨迹跟踪和避障进行了研究。

与固定基机械臂这样的完整系统相比，漂浮基空间机械臂系统的非完整性具体体现在：

（1）当机械臂按照既定关节路径运动后，然后再按照相反的关节路径运动到初始关节位置时，机械臂末端执行器相对于惯性坐标系的位置发生较大变化；

（2）当机械臂按照一定的闭合关节路径运动时，漂浮基体同样不会回到初始位置；

（3）利用漂浮基系统的这种特性，通过输入多个周期性的闭合关节路径，可以以此来调节基体的姿态，最终获得理想的基体位姿状态。

为了更加清楚的了解系统内部的这种耦合关系，必须对系统的非完整性进行深入的讨论[7]。完整与非完整的概念是力学上对约束的分类方式，系统的非完整性体现在系统是否存在非完整约束[8]。漂浮基空间机械臂系统运动特性变得复杂的根本原因是系统内部的某些约束是非完整的。最终，通过对系统运动学[9]分析，进行仿真试验过程。

2 系统动力学一般方程

漂浮基空间机械臂系统是由一个漂浮基体和安装在其上的n单自由度关节机械臂组成的。假设系统处于微重力环境中且不受外力作用；不考虑关节摩擦，按照从基体到末端连杆的方向对各连杆进行编号。

图1 漂浮基空间机械臂系统结构简图Fig.1 Structure Diagram of a Space Based Manipulator System

选择系统广义坐标变量为：基体位姿速度（包括质心线速度和瞬时定轴转速）变量=（，）T∈R6和关节角速度变量φ˙∈Rn，该系统的动力学方程可以表示为[10]：

式中：H（φ）∈R（n+6）×（n+6）—系统广义惯性质量矩阵；

τ∈Rn—作用在n个主动关节上的输入力矩矢量。

对于图1的系统，因为其处于微重力环境，忽略系统势能，

其动能可表示为：

选择漂浮基固连坐标系为参考系，由于系统不受外力干扰且初始动量为零，根据动量守恒定理可知：

式中：Hb（φ）∈R6×6—基座广义质量矩阵；

Hbφ（φ）∈R6×n—基座与机械臂广义耦合质量矩阵。

将式代入式可得，系统关于独立输入关节变量的一般方程：

式中：H*（φ）∈Rn×n—机械臂广义惯性质量，与固定基系统相比，此质量矩阵是此类系统的一般表现形式，当漂浮基惯性参数较之于机械臂较大，甚至是机械臂惯性参数可以忽略时，二者近似相等。

3 系统非完整性分析

本节主要讨论系统的非完整性问题。从非完整性定义出发，给出系统约束类型，根据相关已知条件和判定定理，最终判定系统的非完整性质。另外，从实际系统特征角度考虑，广义坐标存在不可积分项，也可以说明系统在特定方向上是非完整的，那么整个系统就是非完整的。

3.1 系统非完整性判定

约束一般分为几何约束和运动约束两类，几何约束只限制系统的空间位形，约束方程可表示为：

式中：参数 t表示时间，q=［q1，q2，…，qn］T—系统位形的广义坐标向量；n—广义坐标的空间维数。而运动约束不仅显示系统的空间位形，还限制系统的运动速度，其约束方程可表示为：

式中：m—系统独立约束的个数。

然而，在很多实际问题中，运动约束可以实现关于系统广义速度的线性化，即：

当系数矩阵W（q）是行满秩的，且m＜n。此时的约束类型被称为普法夫（Pfaffian）约束。

定义1：n维向量空间Rn中存在两个变矢量域X1（x）∈Rn和X2（x）∈Rn，那么，X1和 X2的李括号运算，可写作［X1，X2］，也是一个n维矢量域，可表示为：

定义2：由一个或几个线性无关的n维变矢量域Xi（x）∈Rn所张成的n维线性子空间被称为一个分布。一般地，这个分布可以用如下形式表示：

定义3：如果一个分布△中任意两个矢量的李括号仍属于这个分布，即该分布内的李括号运算具有闭合性，则称此分布具有对合性。定理1：满足普法夫约束条件的独立速度坐标可积分的充要条件是其组成的分布满足对合性（弗罗贝尼乌斯定理（Frobenius’Theorem））。

3.2 漂浮基空间机械臂系统的非完整性分析

对于图1的系统，定义系统状态变量为系统广义姿态（3-2-1欧拉角 θ=［θ1，θ2，θ3］）矢量，即 y＝（θT，φT）T，输入变量 u=φ˙。由式可知，基体姿态速度矢量与系统关节角速度之间的关系可表示为：

式中：Jωbφ—移动基座相对于机械臂的运动雅克比矩阵。

根据刚体角速度表示变换法则，可知基体姿态矢量对时间的微分与其瞬时定轴角速度之间的关系可表示为：

联立式和式，系统状态方程可以写为：

为了说明系统的完整性，选择系数矩阵K的n个列向量作为n个变矢量域，构成了广义速度分布span（K1，…，Kn）。其中变矢量域 Ki=（a1i，a2i，a3i，eTi）T，ei∈Rn—单位标准矢量。

计算任意两个变矢量域Ki和Kj的李括号，有

式中：矢量 b=（b1ij，b2ij，b3ij，0）T不能恒为 0，即［Ki，Kj］⊄span（K1，…，Kn）。因此系统状态方程所对应的广义速度分布内不满足李括号运算的闭合性，根据定义1、定义2、定义3以及弗罗贝尼乌斯定理可知，漂浮基空间机械臂系统是一个非完整系统。

4 3DOF空间机械臂系统运动学仿真

以三维空间中三连杆漂浮基空间机械臂系统为对象进行仿真，选择整个系统的质心为惯性系原点，并分别在基体质心处以及各连杆关节中心处建立各连体坐标系，基体连体坐标系方向初始时刻与惯性系方向相同。如图2所示。其中，连杆固结矢量a表示系统各连杆质心到相应连杆关节的位置矢量，矢量b表示关节质心到下一连杆关节的位置矢量。矩阵I表示系统各连杆的等效惯性张量，对每一个系统来说，可以将每个刚性连杆的惯性张量矩阵在固结坐标系下用中心惯性张量代替。系统几何惯性参数，如表1所示。

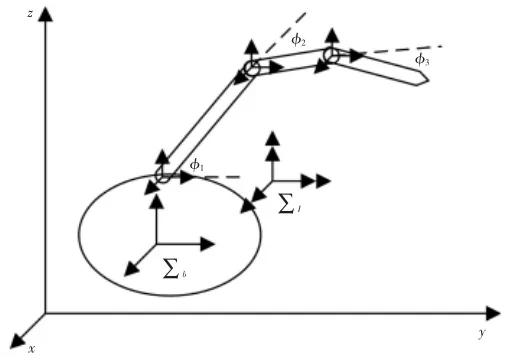
图2 3-DOF空间机械臂系统简图Fig.2 A 3-DOF Space Based Manipulator System

表1 系统相关几何、惯性参数Tab.1 Geometric and Inertia Parameters of the System

设定仿真初始值为关节角度φ=［0；0；0］（系统初始时刻处于展开状态）。以机械臂空载转移过程为研究对象，按照一定的关节控制率τ=K（qd-q）+Dq˙给机械臂关节施加主动关节输入。给定关节目标状态qd=［0.5；-0.2；0.3］，进而规划系统关节路径，获得仿真结果。

仿真结果：仿真过程中关节角的运动轨迹，如图3所示。基体质心位置与姿态所受的响应情况，如图4所示。从以上仿真结果可以看出，与固定基系统不同，当机械臂关节按照一定的控制率运动时，机械臂通过关节1对基体产生力的作用，相应地，基体的位姿受到扰动；反过来，基体位姿的运动又会对机械臂的末端位移和运动精度产生影响。这正是式所描述的系统内部存在的动力学耦合现象。为了更有力的说明系统的非完整性，进行进一步的仿真试验。令关节角继续按关节路径从目标位置qd回归初始位置，如图5所示。基体姿态响应的变化情况，如图6所示。对比仿真结果图4和图6，当机械臂关节完成一个闭环路径时，基体姿态并没有回归到初始状态。因此可以说明，基体姿态的变化过程不仅与系统当前关节角有关，还与关节角运动历史有关，这也恰恰说明了系统的非完整性。

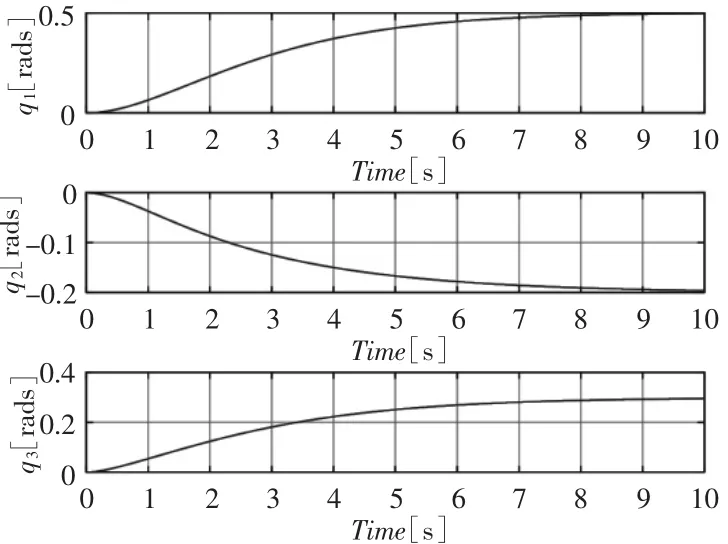
图3 关节角变化轨迹Fig.3 Path of Joints

图4 基体RPY角变化曲线Fig.4 The RPY Angle Curves of a Floating Base

图5 关节路径II（从目标位置回归初始位置）Fig.5 Path II of Joints（From Desirable Configuration to Initial One）

图6 基体RPY角变化曲线IIFig.6 The RPY Angle Curves II of a Floating Base

5 结语

（1）以漂浮基空间机械臂系统为对象，建立了机械表与漂浮基体之间的耦合动力学模型；

（2）讨论了物理系统的非完整特性，并给出了漂浮基空间机械臂系统非完整性的判定过程；

（3）给出两组仿真试验，第一组试验结果表明，机械臂的关节运动会对基体的位姿带来影响，即机械臂和漂浮基体之间存在耦合关系，第二组试验结果表明，系统关节输入条件闭合的情况下，基体位姿没有回到初始状态，这也反映了系统是一个非完整系统。