面向家族制模具多异型腔不平衡充填的快速优化设计
李光明, 郑丽璇, 要小鹏
(1.西南科技大学制造学院,四川 绵阳 621010; 2.西南医科大学医学信息与工程学院,四川 泸州 646000)
0 前言
注射成型作为重要的工业之一,为全球消费市场提供了约35 %的非标产品[1]。产品的小批量和结构多样性要求尽可能地缩短整个生产周期,提高效率,降低成本。因此,采用一模多腔的家族制模具生产不同体积、形状的塑件逐渐成为了研究热点。然而,由于家族制模具往往具有型腔尺寸不一致、浇注系统布置非平衡的结构特点,使得熔体很难均衡充满型腔,从而导致局部模腔充填时间过长、充填不满、过保压等缺陷[2],甚至会造成迟滞效应等,在很大程度上制约了制品的品质。
家族制模具的平衡充填仅依靠工艺参数的调整很难实现,大多数模具设计者通常采用结构修正的方式改善浇注系统的尺寸和布局[3],即首先根据经验或一些设计公式估算流道和浇口的尺寸,然后通过不断试模来调整流道和浇口的尺寸,直到满足制品成型的基本要求。但整个过程花费时间较多,成本过高。目前,一些研究常将型腔同时充满作为熔体充填平衡的指标[4-5],但对于各异型腔的充填,并不充分。文献[6]建议采用制品的体积收缩率作为均衡性的指标,但体积收缩率通常是指从保压阶段结束到制件冷却至环境参考温度时局部密度的百分比增量,很难从整个成型过程来描述型腔充填的平衡性。还有一些文献[7-8]分别以制品质量容差或最小流道体积为目标,所获得的流道设计方案很难达到真正的最优。此外,模流分析平台Moldflow提供了Runner Balance模块,采用变截面方法优化分流道截面尺寸,从而达到型腔充填流动和压力的近似平衡,很多文献[9-10]直接采用此模块对流道平衡进行优化设计。但是该模块未能综合考虑对分流道长度及间距的优化,这样面对数量较多的异形型腔结构时可能会使迭代效率较低,而且仅能适用于部分网格模拟,应用的范围较为局限。鉴于此,本文提出采用不同型腔间充填末端的最大平均压力差作为不平衡因子,压力均衡可保证多模腔间的流动均衡,更大程度地提高合格产品的比例,并提供更宽的成型范围[11];也可以从侧面反映制件收缩的状况。针对指示灯柱组合产品的总体几何结构,集成的快速优化机制可以合理调节模具分流道的截面、长度及间距尺寸,以获得型腔充填近似平衡的优化目标。
1 多异型腔熔体流动充填平衡的机理分析
模具流道布局有着使塑料熔体平稳地转换流向、均衡分配给各个型腔的功能[12]。流道截面形状和长度等尺寸的变化,会引起熔体压力、流速和流量的变化,给模具型腔的充填平衡带来重要的影响。
现假设塑料熔体为不可压缩,流道壁面上流动速度为零,无滑移现象,熔体黏度不随时间变化,忽略流动过程中黏滞性剪切变形所造成的能量转变。流道内熔体周向速度(vθ)和径向速度(vr)为零,且轴向速度(vi)、剪切应力(τij)对于周向(θ)和轴向(z)的导数为零。圆柱面坐标系的轴向z的动量方程可以简化为:
(1)
式中 ∂p——压力差,Pa
∂z——单位轴向长度,m
r——任意截面半径,m
τ——剪切应力,Pa
塑料熔体在圆形流道的轴向z流动的状态方程为:
(2)
式中K——稠度,Pa·s
γ——剪切速率,s-1
n——流动指数
∂v——流动速度,m/s
将式(2)带入式(1),根据流动模型的边界条件,对整个流道的截面积分可以得到塑料熔体在流道内流动的体积流率方程:
(3)
式中qv——体积流率, m3/s
R——圆管截面半径,m
从式(3)可以看出,在单一流道内,熔体流动的体积流率、流道压降Δp、流道截面半径R和长度L有密切的联系。通过调节流道截面半径R和长度L可以调整塑料熔体进入型腔的流量和压力降,可用于改善成型过程中充填分布的均匀性,实现多个型腔近似平衡充满,并在可接受的范围内,提高了制件的品质。
2 指示灯柱产品结构与材料选用
整体几何模型为指示灯柱产品的组合,单个制件的形状为短粗形圆柱体,结构比较简单。5个制件的结构、大小尺寸不完全相同,最大的零件直径为8.5 mm,总的高度为9.1 mm,最小制件的直径为4.7 mm,总高为6.5 mm。本文采用Moldflow软件作为模拟试验分析平台,由于指示灯柱产品的截面较厚,故采用Solid 3D网格,网格最大边长设置为3,材料选用聚甲基丙烯酸甲酯(PMMA),产品模型如图1所示。

图1 3D网格模型Fig.1 3D mesh
3 平衡充填优化机制的集成
平衡充填设计是一个带约束多维变量复杂模型的优化问题。在对多异形腔的总体流道结构构建的基础上,集成了多种方法和策略,深入挖掘设计变量与不平衡因子间的非线性隐式关系,以获得指标最优的流道结构方案,为注塑模具设计人员提供快速方便的决策依据。
3.1 流道布局与设计变量
流道布局与设计的合理性对于提高充填平衡有很大的影响,总体系统结构采用I型非平衡式布置,体积较大的制件靠近主流道位置一侧。在此重点考察了组成流道系统的14个尺寸,次分流道长度X1、X2、X3、X4、X5,次分流道之间的距离L1、L2、L3、L4及次分流道截面半径R1、R2、R3、R4、R5的14个因素对各异型腔充填均衡的影响,如图2所示。

图2 流道总体布局Fig.2 The overall layout of the runner
3.2 试验方案的选用设计
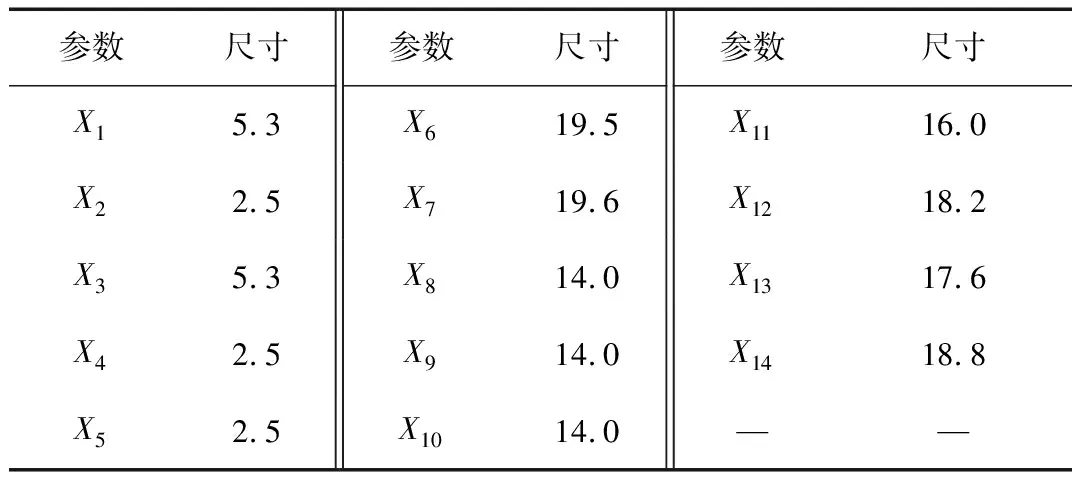
流道系统的几何布局共有14个设计变量,为了提高后期拟合精度和统计显著性,需要设置更为散布的水平。均匀设计,又称为空间填充设计,其数学原理是数论中的一致分布理论,将数论和多元统计相结合,属于伪蒙特卡罗方法的范畴[13]。均匀设计考虑试验点在设计范围内的均匀散布,保证了试验点具有均匀分布的统计特性,为了考察每个因素变量的更多水平。根据指示灯柱产品材料特性和成型的实际经验,选取合适区间作为设计变量的取值范围,设置如表1所示,试验方案选用U29(2928),对流道截面半径、长度及间距等设计变量进行了均匀的搭配。

表1 设计变量水平的设置范围Tab.1 The setting range of design variable level
3.3 神经网络多维非线性逼近模型的构建
流道几何布局的多维结构变量与不平衡因子之间的关系非常复杂,很难用一般的回归数学模型进行描述。BP神经网络(back propagation)具有较为强大的时变性和非线性函数逼近能力,几乎可以逼近所有的非线性隐式函数[14]。本文采用双隐含层的前馈神经网络来逼近两者间的非线性映射关系。将试验方案中流道结构变量作为BP神经网络的输入矢量,不平衡因子值作为神经网络的预测矢量,隐层采用sigmoid型传递函数,输出层采用线性函数,网络的输出可表示为:
a=f(wp+b)
(4)
式中f——输入/输出关系的传递函数
w——权值
a——输出
p——输入
b——神经元偏置
3.4 混合遗传算法
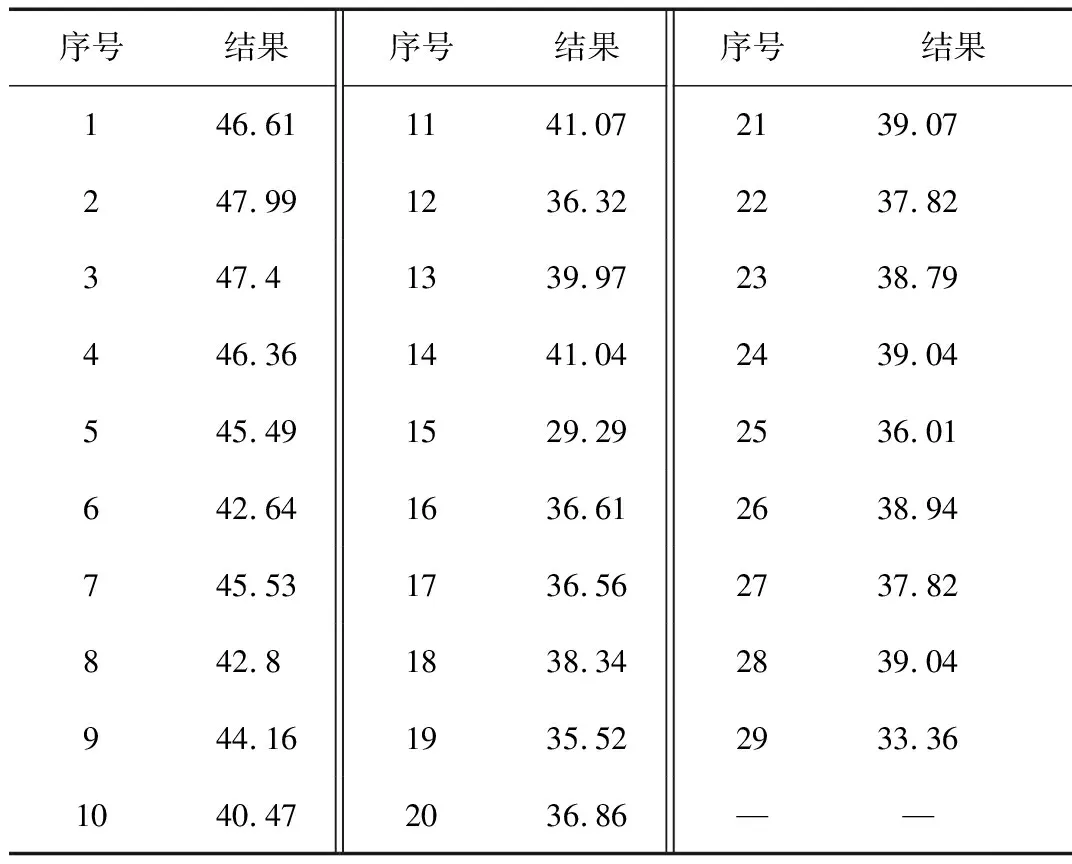
遗传算法(genetic algorithm,GA)是基于自然选择和基因遗传学原理的进化搜索算法[15],GA随机生成初始种群,通过选择、交叉、变异等方式产生新的个体来仿真生物的基本进化过程,利用适应度函数表征不平衡因子解的优劣、引导种群的进化方向。通过种群持续地更新,降低平均适应度,进而逼近问题的全局最优解。GA具有鲁棒性强、简单高效等特点。然而,单一的GA容易产生“早熟”现象,一旦局部个体在种群中占有强势,会使多样性迅速降低,进化能力基本丧失,搜索范围变窄,陷入局部极值点。依据模拟退火的Boltzmann生存机制可以使生物种群的多样性和优良性得以复制和继承,避免种群过早收敛于局部区域[16]。其优化策略为:随机产生新群体的个体适应度(f),变动阈值为fpro,初始退火温度为T0,执行温度为TK,终止温度为TE,如果f f(x)=PΔ=Yga(r1~r5,X1~X5,L1~L4) (5) 其中,PΔ为不平衡因子,从工程意义上看,不同型腔熔体充填末端的最大平均压力差越小,则熔体在各型腔内充填过程越均衡。 通过均匀设计以较小的试验方案,较好地反映了全面试验的主体特征,采用数值模拟得到不平衡因子ΔP的结果如表2所示。 表2 均匀设计试验结果Tab.2 Experiment results from the uniform design 通过Matlab建立BP神经网络模型,设定隐含层神经元数目为16,其中70 %的实验数据用于网络的训练,剩余数据用于检验网络的泛化,并确定网络权值。经过6步迭代后,网络误差达到要求。通过验证,R值均在93 %以上,表明神经网络对数据的拟合程度较好,映射了不平衡因子与结构变量间的逼近关系,训练和验证结果如图3所示。 ○—数据 ----拟合 Y=T(a)训练R值 (b)验证R值图3 验证结果Fig.3 The verification results 对构建多维变量神经网络模型进行遗传算法的优化,边界条件如表1所示,即为流道系统各设计尺寸的变化范围,通过迭代得到模型适应度的最小值为10.177 6,迭代过程如图4所示,最后得到的最优流道系统结构尺寸经过圆整后如表3所示。 1—最优适应度 2—平均适应度图4 优化迭代过程Fig.4 The optimum iterative procedure 参数尺寸参数尺寸参数尺寸X15.3X619.5X1116.0X22.5X719.6X1218.2X35.3X814.0X1317.6X42.5X914.0X1418.8X52.5X1014.0—— 考虑到试验样本数量、逼近模型和遗传算法的局限性以及尺寸圆整带来的误差,因此,有必要通过进一步的数值模拟验证流道系统的最优解。在Moldflow分析平台中重构相应的结构尺寸,通过模拟得到不平衡因子ΔP≈15 MPa,结果如图5所示。 图5 最大平均压力差ΔPFig.5 The maximum average pressure difference 流道系统的结构尺寸修正后,使得注射处位置压力和锁模力有了较大程度的改善,其中试验方案中最大注射位置压力由73.81 MPa经优化后降至47.27 MPa,如图6所示。 (a)优化前 (b)优化后图6 注射位置压力Fig.6 Pressure at the injection location (a)优化前 (b)优化后图7 最大锁模力Fig.7 The maximum clamping force 注射成型的最大锁模力由试验方案中的16.02 t经优化后降至9.22 t,如图7所示。上述说明了熔体在不同型腔内流动的近似平衡能极大地避免了模具内部的局部过保压,飞边等缺陷,使型腔间压力分布较为均匀,同时也降低了设备的能耗,节省了成本。 (1)通过调节流道系统截面半径、长度及间距等尺寸可以平衡塑料熔体进入各个型腔的流量和压力,更好地实现了多个异型腔的近似均衡充满,优化后型腔间充填末端的最大平均压力差ΔP约为15 MPa,远远低于试验方案中的数据;锁模力和最大注射压力有较大的下降; (2)集成的快速优化机制可以高效地解决家族制模具多异型腔的流道结构优化问题,得到一组满足近似均衡充填的流道系统几何结构参数。4 结果与讨论
4.1 多维非线性逼近模型的构建

4.2 运用遗传算法寻优

4.3 试验验证


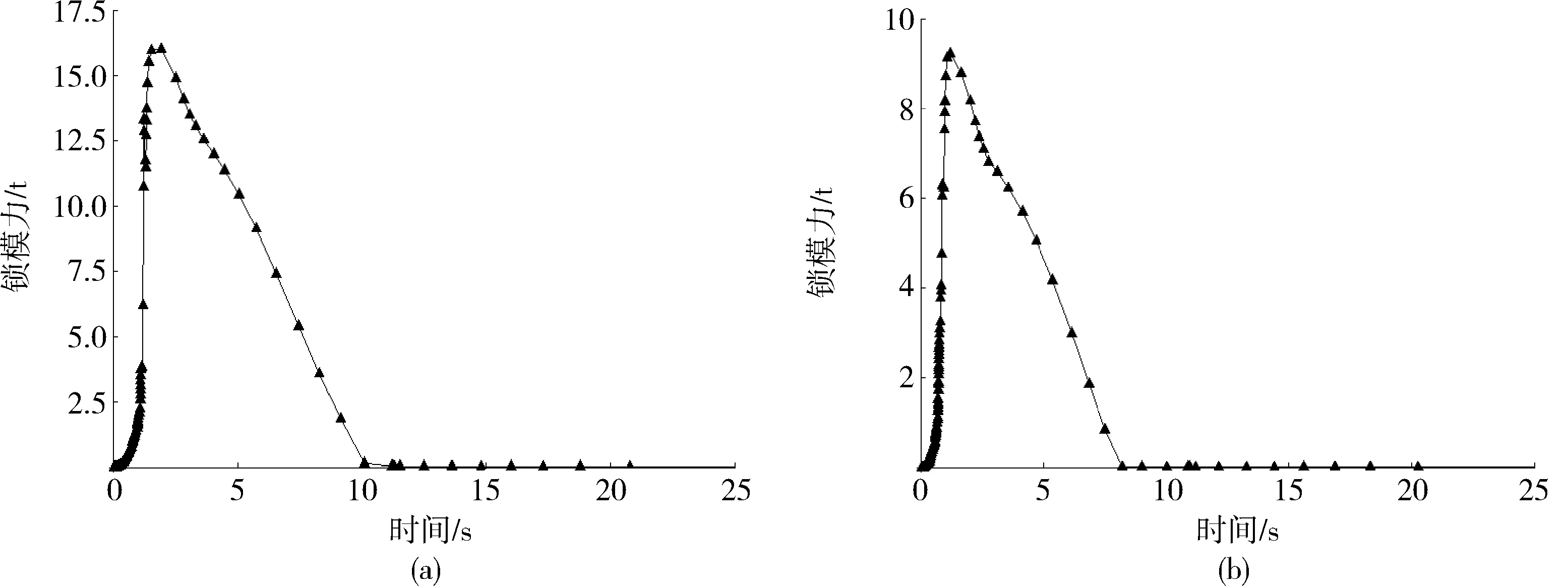
5 结论

