基于横摆力矩的轮胎侧向力估计算法

赵林峰 杨 军 张荣芸 陈无畏

1.合肥工业大学汽车与交通工程学院，合肥，230009

2.安徽工程大学机械与汽车工程学院，芜湖，241000

0 引言

随着人们对汽车操纵性和安全性要求的日益提高，汽车侧向主动安全控制系统得到了极大的关注与发展。轮胎侧向力是汽车主动安全控制系统对汽车进行稳定性控制的一个关键参数，该参数的准确与否能够直接影响主动安全控制系统如电子稳定性程序（electronic stability program，ESP）的性能。目前，轮胎侧向力传感器高昂的成本以及一些技术上的困难，导致现有汽车几乎没有装备可直接测量出轮胎侧向力的传感器，因此，利用现有传感器信息来估算轮胎侧向力显得尤为重要。目前已有专家学者在此方面做了大量的研究工作［1-5］。轮胎与路面之间的纵向力和侧向力是2个非常复杂的物理量，对其进行描述的数学模型主要有Magic formula轮胎模型、Fila轮胎模型和Dugoff轮胎模型等［6］。但在运用上述模型时，需要在线实时检测路面附着系数，即便对轮胎模型做了大量简化（如LuGre轮胎模型［7］），其结果还是呈现非线性，从而导致估计器及控制器的控制算法设计变得十分复杂。此外，轮胎的侧向力与纵向力之间的耦合，也会对估计器和控制算法的鲁棒性产生影响。

基于上述问题，本文提出了一种基于横摆力矩的轮胎侧向力估计算法，避免运用复杂的轮胎模型。假设轮胎纵向力已知，将4个轮胎侧向力作为汽车动力学模型的未知输入量。该算法的优点不仅在于极大地简化了估计算法，且不需要实时检测路面附着系数，增强了汽车在各种附着系数路面稳定行驶的鲁棒性。

1 汽车动力学以及横摆模型

1.1 汽车动力学模型

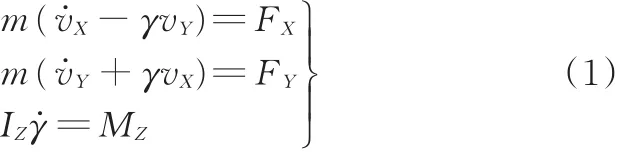
图1所示的七自由度非线性汽车动力学模型主要包括纵向、侧向、横摆运动和4个轮胎的回转运动，数学表达式如下：式中，FX、FY分别为沿X轴和Y轴方向的汽车纵向合力和侧向合力；m为整车质量；vX、vY分别为质心的纵向速度和侧向速度；γ为横摆角速度；MZ为汽车横摆力矩；IZ为整车绕Z轴转动惯量。

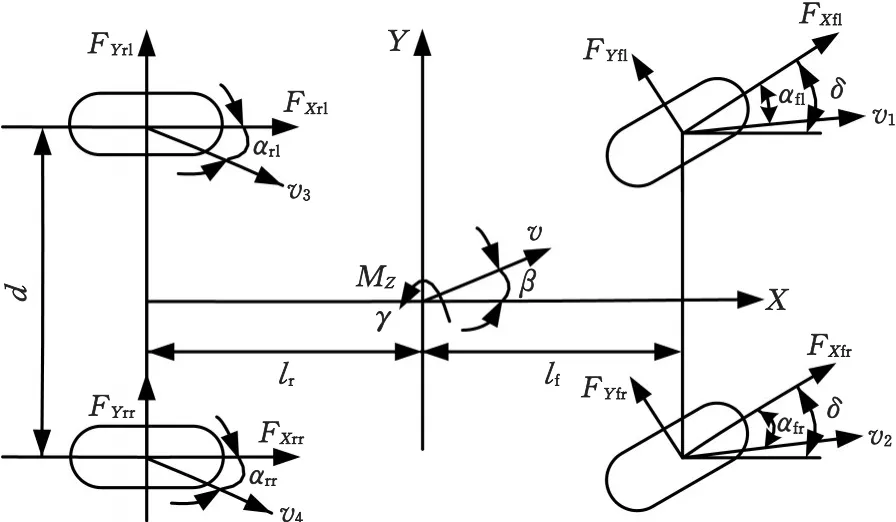
图1 整车模型Fig.1 Whole vehicle model

1.2 横摆动力学模型

假设汽车质心已知，针对质心O点、左后轮O1点、左前轮O2点、右前轮O3点和右后轮O4点等5个旋转中心来计算出横摆力矩，具体公式如下。

（1）质心的横摆力矩：

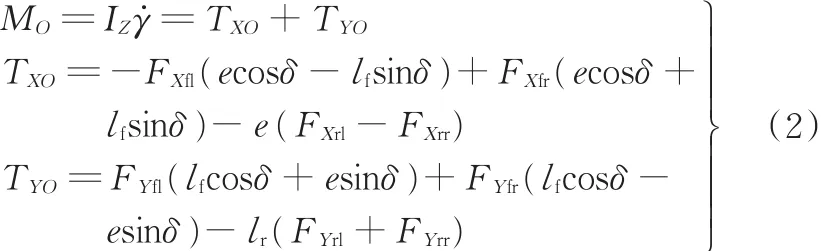
（2）左后轮旋转中心横摆力矩：

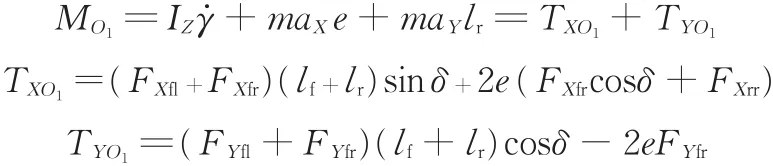
（3）左前轮旋转中心横摆力矩：

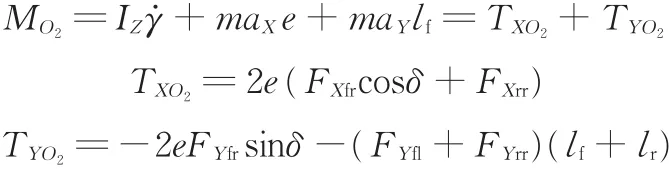
（4）右前轮旋转中心横摆力矩：

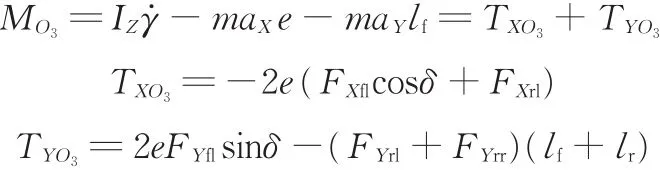
（5）右后轮旋转中心横摆力矩：

式中，δ为前轮转角；aX、aY分别为纵向加速度和侧向加速度；FXi、FYi分别为轮胎上的纵向力和侧向力，i=fl、fr、rl、rr分别表示汽车左前轮、右前轮、左后轮、右后轮；MOj（j=1,2,3,4）为各旋转中心的横摆力矩；lf、lr分别为整车质心至前轴和后轴的距离；e为轮距一半；TXOj、TYOj分别为各旋转中心纵向力和侧向力产生的横摆力矩。

以上各式可以通过矩阵表达如下：

式中，c代表cos；s代表sin。

1.3 基于干扰观测器的侧向力横摆力矩估计

通过横摆动力学模型，结合横摆角速度和纵/侧向加速度等物理量估算出式（3）中所述的5个旋转中心的侧向力横摆力矩，再由侧向力横摆力矩计算出各个轮胎侧向力。

假设汽车的质心位置已知，图2为轮胎侧向力估计结构图。由线性二自由度模型可计算出车辆的横摆角速度名义值（期望值）［8］。首先通过G矩阵计算出轮胎的纵向横摆力矩，并作为实际横摆动力学与名义横摆动力学模型的输入。侧向力横摆力矩则由轮胎侧向力通过H矩阵计算得出。引入PID控制器是为了保证更好的跟踪效果，其控制输入为实际横摆角速度γ和名义横摆角速度γ̂之差。若实际（测量）横摆角速度能够很好地跟踪名义横摆动力学模型，这表明反馈控制器的输出能够补偿轮胎侧向力产生的力矩。最后通过最小二乘法和垂向力比例权重估算出实时侧向力。

图2 轮胎侧向力估计结构图Fig.2 Tire lateral force estimation structure diagram

假设4个轮胎纵向力已知，以质心O点为例，估算其侧向力横摆力矩。TXO可以通过式（2）计算得到，因而TYO在横摆角加速度γ̇的基础上计算得到。所用的方法如下［9］：

⇓拉普拉斯转换⇓低通滤波

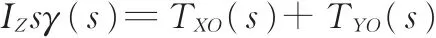
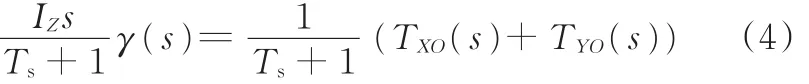
对上式状态方程进行变换得

式中，s为拉普拉斯变换复变量；Kp、Ki、Kd分别为PID控制器的比例、积分和微分可调参数；γ̂为横摆角速度γ的名义值；TXO为观测器的输入值；TˉYO为质心侧向力横摆力矩的初始值；γ͂为横摆角速度的测量值与名义值之差；Ts为时间常数。

将式（5）减去式（4）得

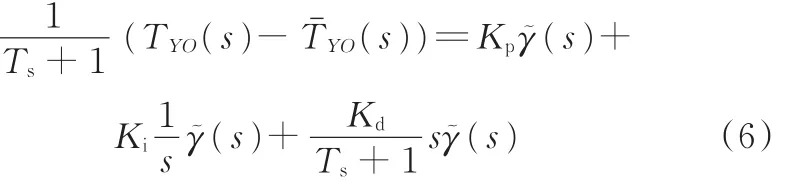
从而可得到旋转中心O点的侧向力横摆力矩估计值：

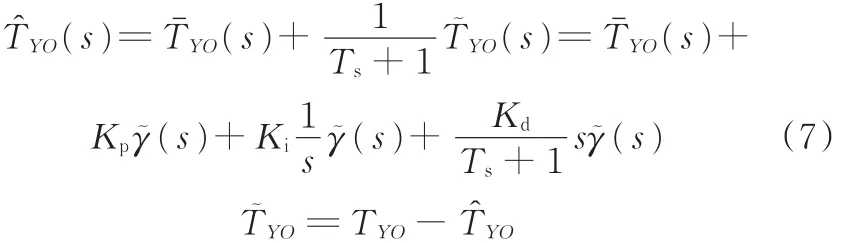
从式（7）中可以看出，时间常数Ts越小，得到的摩擦力差值频率带越宽。但T̂YO不适合取太高的频率值，因为需要利用滤波器从差值信号γ͂中削弱噪声的影响以及在低频带中估计出PID控制器的差分值。其他各旋转中心的侧向力横摆力矩计算同上。

2 轮胎侧向力估计

由式（3）可知，通过关于前轮转角的矩阵H可建立各个轮胎侧向力与侧向力横摆力矩之间的关系，因此，可利用基于干扰观测器的侧向力横摆力矩估计方法估算出侧向力横摆力矩［10］，并以此分别估计出各个轮胎的侧向力。

通过已估计出的转矩信号T̂Y和式（3）中侧向力与侧向力横摆力矩之间的关系，利用最小二乘法来估计出轮胎侧向力，即找出一个合适的矢量F̂Y满足下式中的条件［11］：

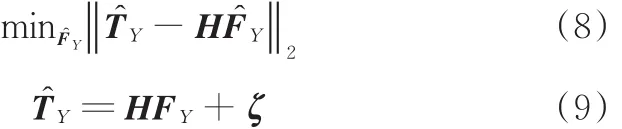
其中，ζ为横摆力矩估计的误差值，是模型参数的不准确所导致，如汽车质量、横摆惯性及轮胎纵向力不准确等。无约束最小二乘法的解析解表达式如下：

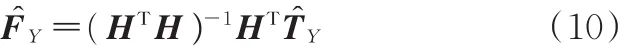
横摆力矩估计的误差值ζ由零均值随机信号组成。然而，式（10）中的二次型指标函数最小唯一解的充分必要条件是矩阵H的阶数应该与列秩的大小相等（即矩阵HTH是可逆的）。

当前轮转角为零（或极小）时，矩阵H的阶数不能满足当前列秩的情况。证明如下：

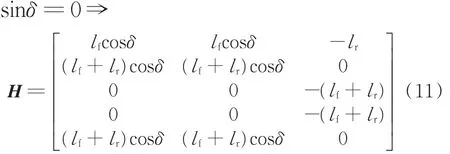
从式（11）中可以看出，矩阵的H第一列和第二列完全相同，因此，此时矩阵的列秩不能满足方程所需。显然，当前轮转角足够小时，式（11）中的列秩将小于列数，故矩阵H无解。尽管这只是矩阵H由于缺失列秩而导致无解的一种情况，但当控制器作逆向运算时仍会发生数值出现错误的情况。

为了克服列秩带来的上述问题，式（3）需要进行适当的修改：①前轮转角可以取零，②分析轮胎侧向力和其力矩之间的静态关系。

（1）针对参考点O：

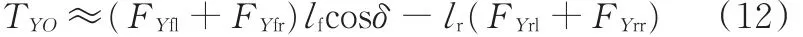
（2）针对参考点O1：

（3）针对参考点O2：

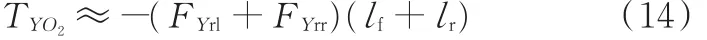
（4）针对参考点O3：

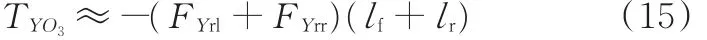
（5）针对参考点O4：

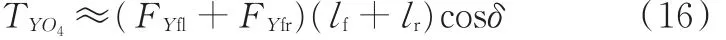
将上述公式进行合并，可得到如下方程：

由此可以写成如下状态方程：

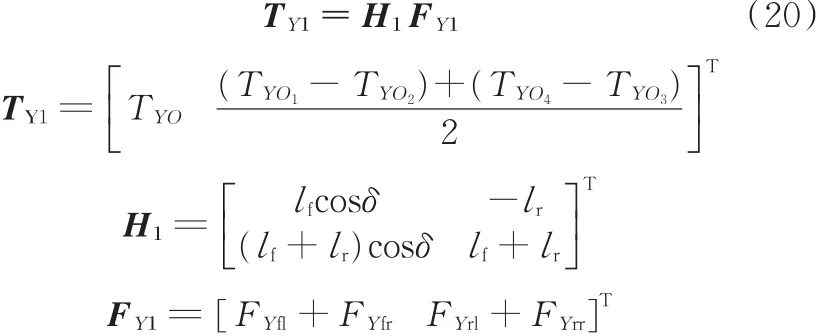
从而得到当前轮转角为零（或极小）时的侧向力估计值为

依据垂向载荷的大小按比例分配前轮侧向力，得

其中，λ为常数，属可调参数。

3 仿真计算

基于上述整车动力学模型和横摆动力学模型，在MATLAB/Simulink环境中进行仿真，其中整车部分参数见表1。仿真工况为双移线工况和鱼钩工况，分别见图3和图4。仿真条件为车速80 km/h，路面附着系数分别为0.8和0.2。

为了验证模型的准确性，在CarSim中建立相同参数的汽车模型，并在相同系统输入的情况下，对比系统的输出。本文利用CarSim中的输出响应代替实车试验数据，与MATLAB/Simulink中的仿真模型输出响应作对比分析，以验证仿真模型的准确性。

从图5～图6中可以看出，在双移线工况下，相对于路面附着系数为0.8时的轮胎侧向力，路面附着系数为0.2时的轮胎侧向力大小明显偏小，这是由于路面提供的轮胎附着力小，从而导致轮胎侧向力减小。此外，基于MATLAB/Simulink搭建模型估计得到的轮胎侧向力和在CarSim中仿真得到的轮胎侧向力，无论在路面附着系数为0.8或0.2时，其结果基本一致。由此可知，本文提出的轮胎侧向力估计方法的估计效果良好。

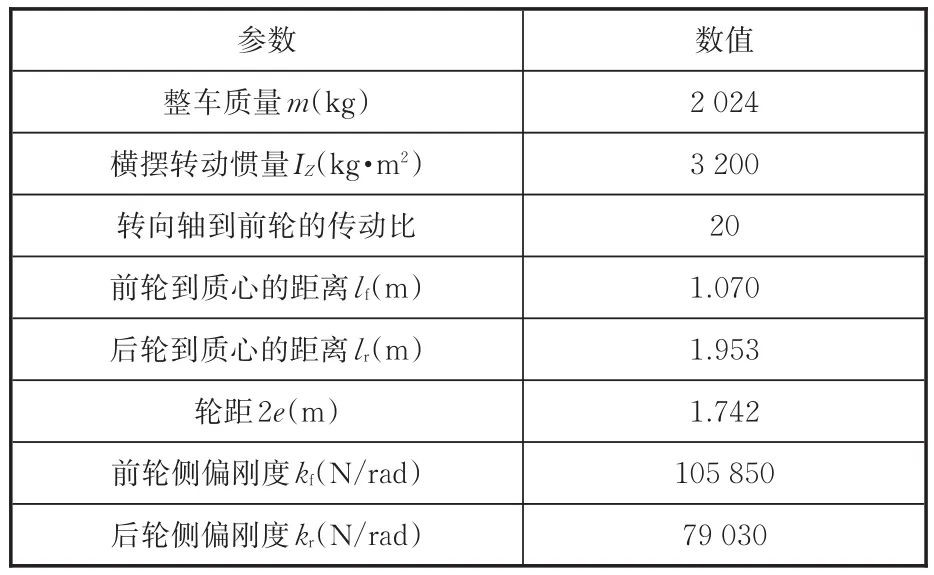
表1 部分汽车结构参数Tab.1 Part of the car structure parameters

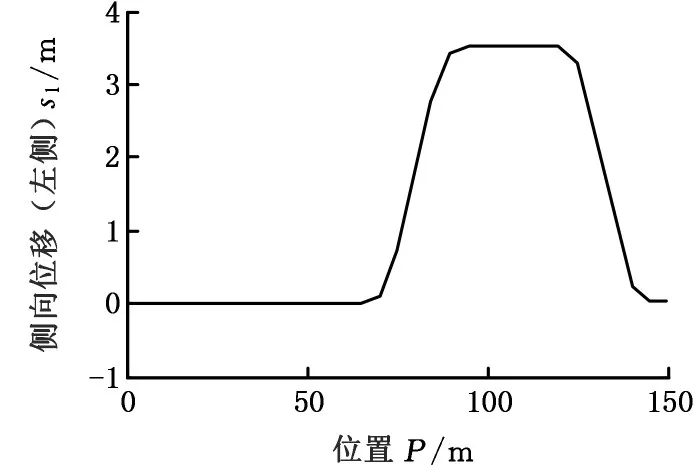
图3 汽车行驶路径（双移线工况）Fig.3 Car driving path（double lane change working condition）

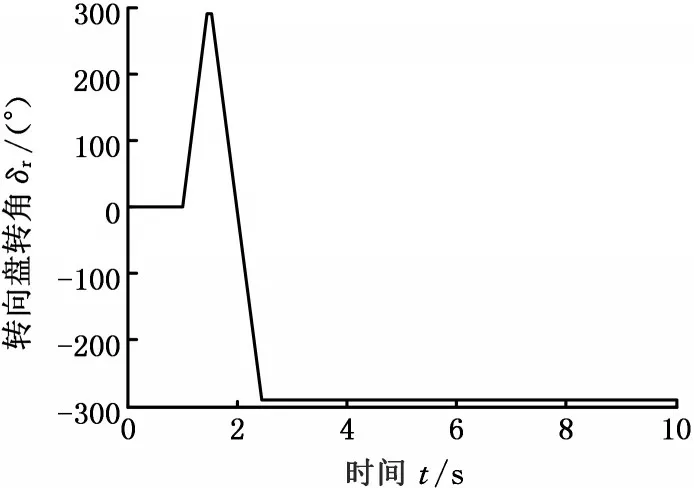
图4 汽车行驶路径（鱼钩工况）Fig.4 Car driving path（fishhook working condition）

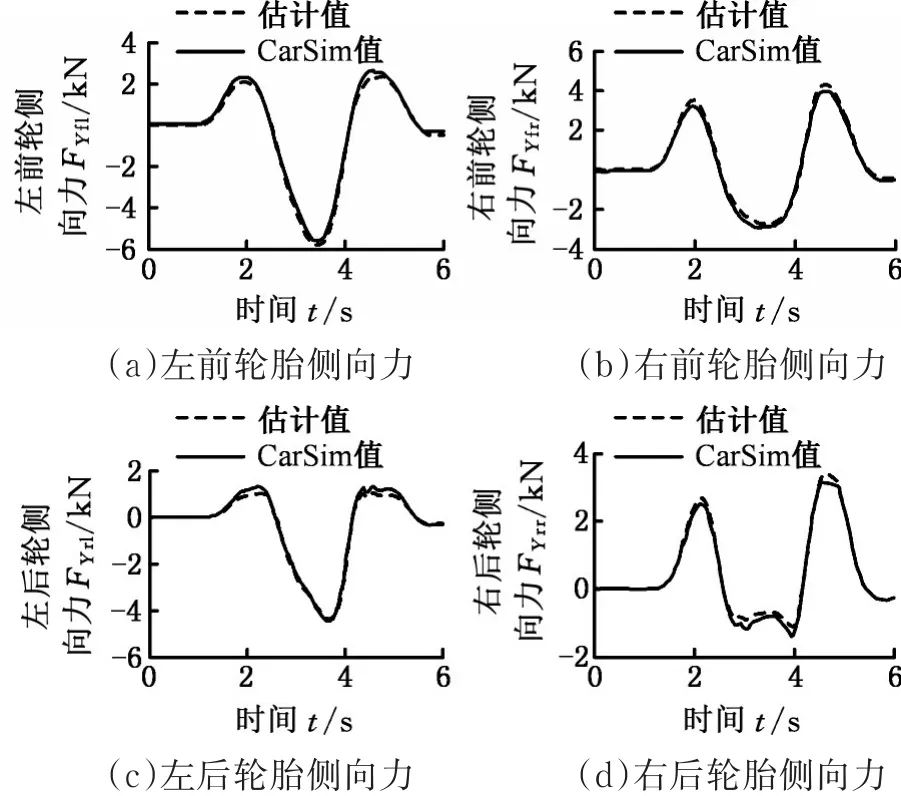
图5 μ=0.8时双移线工况下四轮胎侧向力CarSim数据Fig.5 Four tire lateral force CarSim data at μ=0.8 under the working condition of double lane change

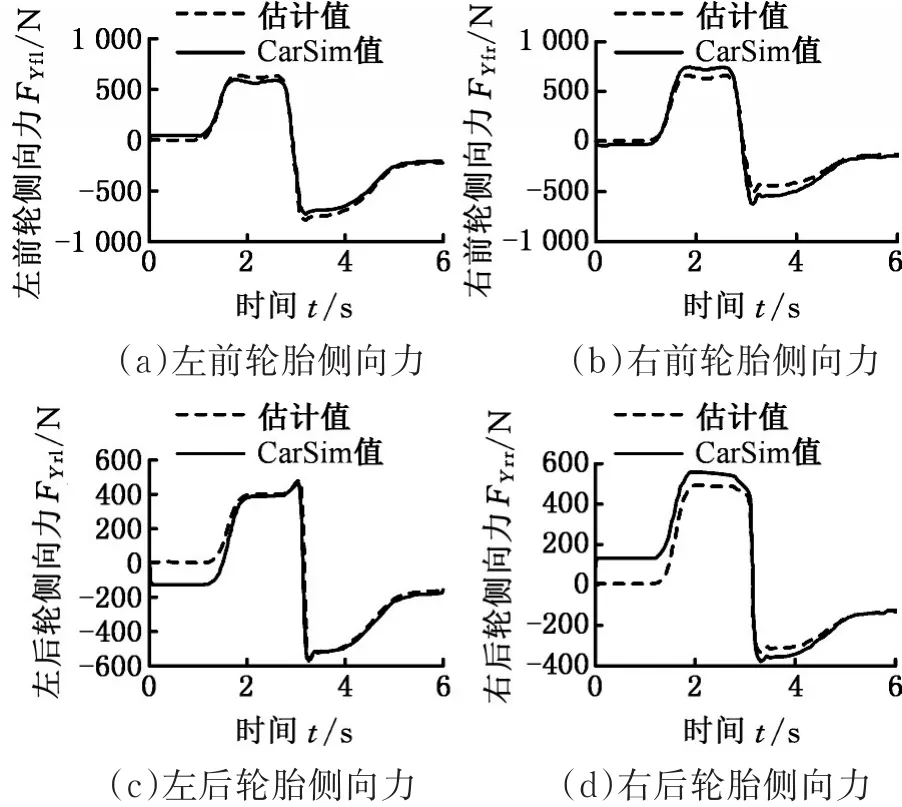
图6 μ=0.2时双移线工况下四轮胎侧向力CarSim数据Fig.6 Four tire lateral force CarSim data at μ=0.2 under the working condition of double lane change

图7为汽车行驶轨迹为鱼钩工况的曲线，可以看出，当路面附着系数为0.8时，估计值曲线与CarSim值曲线基本匹配。当路面附着系数为0.2时，仿真结果表明汽车已经失稳，轮胎侧向力趋近于无穷大，因此该图未给出。

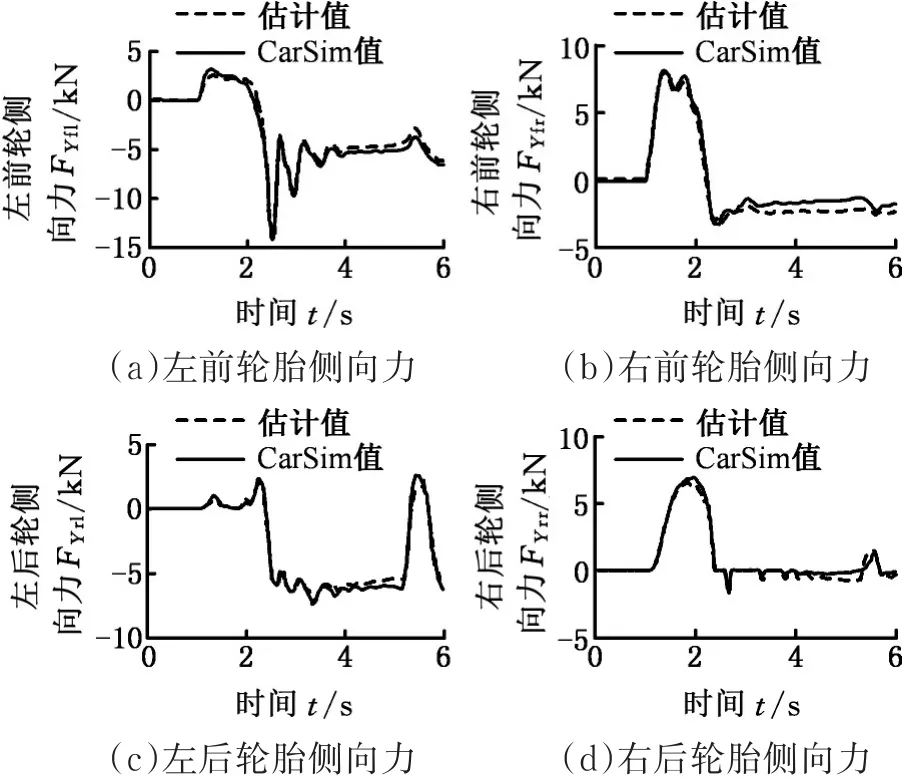
图7 μ=0.8时鱼钩线四轮胎侧向力CarSim数据Fig.7 Four tire lateral force CarSim data at μ=0.8 under the working condition of fishhook

4 硬件在环仿真试验

为充分验证基于横摆力矩侧向力估计算法的有效性，在仿真试验的基础上进行硬件在环试验验证。建立了装配有自行改制的电子稳定性程序（ESP）系统的硬件在环仿真平台，利用ESP系统以及本文中提供的控制算法估算出汽车的轮胎侧向力。ESP控制系统采用飞思卡尔MC9S12XS128为其控制单元。根据相关汽车参数在veDYNA中建立整车模型和虚拟试验场地，并在PC机中实时运行，控制器输出信号可通过接口系统分别与ESP液压系统中的电磁阀相连；硬件系统为该试验车的液压系统、各种车载传感器等；接口系统能将硬件系统中的传感器信号采集并处理，从而实现与软件系统中运行的整车模型及控制器进行信息实时交换。硬件在环仿真平台见图8。

图8 硬件在环仿真平台Fig.8 Hardware in-loop simulation platform

硬件在环测试主要通过LabVIEW的I/O接口使ESP系统能够控制运行于LabVIEW中的汽车模型，同时通过控制器局域网（controller area network，CAN）将模型运行结果转化后，再传给ESP系统构成反馈回路。

试验设备主要包括汽车制动液压系统、各种传感器、开发的ESP控制器、改制的ESP液压控制单元、LabVIEW的PXI主机、SCB-68接线板、PC机等。硬件在环试验在虚拟的干燥路面上进行，车速设定为80 km/h，虚拟道路附着系数为0.8，试验具体结果见图9～图12。为了验证该预测模型的普遍适用性，在进行硬件在环测试时，采用了正弦波半波试验（连续两次转向盘正弦输入，且第二次的幅值小于第一次的幅值）模拟高速连续同侧避障的危险性工况。

图9 左前轮硬件在环试验曲线Fig.9 Left front wheel hardware in-loop experimental curve

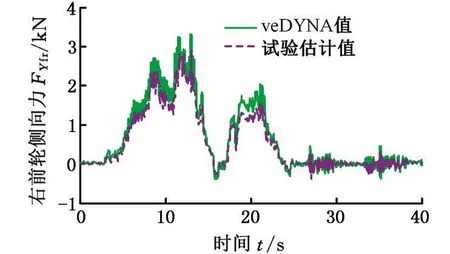
图10 右前轮硬件在环试验曲线Fig.10 Right front wheel hardware in-loop experimental curve

图11 左后轮硬件在环试验曲线Fig.11 Left rear wheel hardware in-loop experimental curve

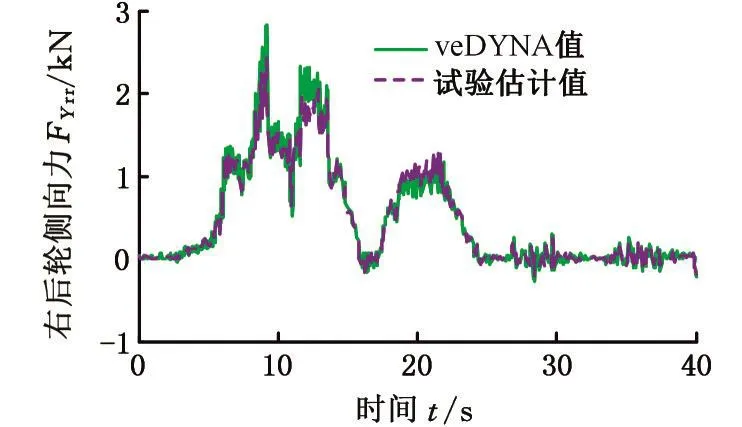
图12 右后轮硬件在环试验曲线Fig.12 Right rear wheel hardware in-loop experimental curve

从图9～图12中可以看出，通过硬件在环试验得到的估计值与veDYNA值（直接取自veDYNA汽车模型中实时运行时所对应的侧向力）的结果基本保持一致，表明本文提出的估计方法能够很好地估计出轮胎侧向力。

5 结论

（1）文中提出了一种基于横摆力矩的轮胎侧向力估计算法，通过基于MATLAB/Simulink和CarSim对比仿真试验，可以看出，估计的轮胎侧向力与CarSim中轮胎侧向力无论在路面附着系数为0.8或0.2时，其结果基本一致。

（2）对所采用的基于横摆力矩的轮胎侧向力估计算法进行了硬件在环试验验证，可以看出，veDYNA汽车模型实时运行中的轮胎侧向力（即测量值）与硬件在环试验中得到的轮胎侧向力估计值的结果相一致。

（3）本文所提出的基于横摆力矩的轮胎侧向力估计算法，其优点不仅在于极大的简化了估计算法，避免运用复杂轮胎模型，且不需要实时检测路面附着系数，增强了汽车在各种附着系数路面稳定行驶的鲁棒性。