弯曲钢丝绳股内钢丝张力变化仿真与实验

李 伦 赵德阳 李济顺， 薛玉君 邹声勇 马 伟 杨少东

1.河南科技大学河南省机械设计及传动系统重点实验室，洛阳，471003

2.河南科技大学机电工程学院，洛阳，471003

3.矿山重型装备国家重点实验室（中信重工机械股份有限公司），洛阳，471039

0 引言

钢丝绳在矿山提升机的工作过程中有非常重要的作用，其安全性能直接影响人员的生命安全和物料的安全运输。当钢丝绳绕经天轮弯曲承载时，由于各丝轴向应变不同，其张力也不相同，导致绳丝之间产生内摩擦力。当多次循环反复弯曲及承载超过钢丝绳强度极限时，就会发生断丝失效等严重故障［1］，因此研究分析钢丝绳绕经天轮弯曲受载时各丝张力的变化，对提高矿井的安全生产水平和延长钢丝绳使用寿命具有十分重要的意义。

国内外学者在钢丝绳弯曲张力方面已作了许多研究，但由于钢丝绳本身具有相互缠绕的复杂构造，且钢丝绳-天轮接触区域存在不确定性，故建立钢丝绳的精确模型仍是一个难题。YU等［2］建立的钢丝绳有限元模型精确地分析了直线段钢丝绳股内钢丝之间的受力情况，该模型主要由梁单元与弹簧单元组成，采用螺旋排列的短梁单元模拟螺旋钢丝，径向放置的刚性梁代替钢丝截面，利用弹簧单元来捕捉接触面的挤压与相邻钢丝之间的摩擦。JOLICOEUR等［3］建立了钢丝绳在受到弯曲、拉伸和扭转载荷时的半连续数学模型，该模型在拉伸和扭转载荷下可提供非常准确的结果，但在弯曲载荷下验证其正确性较为困难。CHIANG［4］探讨了在轴向载荷作用下，单股钢丝绳的轴向刚度和轴向应力增大的主要影响因素。JIANG［5］利用有限元软件在钢丝的接触区域对三维实体进行更加精准的离散处理，建立了一种精确有限元模型来研究钢丝绳，其结果与COSTELLO［6］设计的线性弹性股模型结果相吻合。STANOVÁ等［7-8］推导出钢丝绳参数方程，预测了钢丝绳在拉伸载荷下多层股的应变变化行为。贾小凡等［9］通过实验研究证明了钢丝绳磨损后，其断丝多发生在接近钢丝绳捻距整数倍的地方。WANG等［10-11］建立了6×19+IWS钢丝绳有限元模型，对钢丝微动磨损和疲劳寿命进行了有限元分析。NAWROCKI等［12］考虑了钢丝之间所有可能的运动，建立了单股钢丝绳的有限元方程，分析得到即使是小幅度的弯曲仍可显著影响轴向承载钢丝绳内各丝张力分布的规律。马军等［13］分析并验证了不同位置的钢丝在其轴向应力呈螺旋状分布，在钢丝截面上应力呈中心对称分布的规律。MA等［14］、郭卫等［15］分析了钢丝绳各丝的空间几何位置关系，推导出圆弧弯曲各钢丝的中心线参数方程，并利用多种方法建立出实体模型，为弯曲状态下钢丝绳的分析提供了可能。

上述文献大多通过有限元方法对钢丝绳弯曲时各丝的应力、张力进行研究，其值的变化主要与钢丝绳捻距、钢丝所处捻绕位置等有关，但并未涉及钢丝绳股内张力的变化与天轮接触弧长的关系。本文以1+6型钢丝绳股内各钢丝为研究对象，应用CATIA软件建立几何模型并将其导入ABAQUS中，定义符合实际工况的边界条件，得到绕经天轮弯曲承载钢丝绳股内各丝的张力分布与接触弧长的影响规律，并通过实验对其进行验证。

1 钢丝绳弯曲张力有限元仿真

1.1 弯曲钢丝绳模型

图1所示为钢丝绳绕经天轮弯曲承载时的简化模型。在钢丝绳中心处放置一个与钢丝绳接触的天轮，由于天轮和钢丝绳作用区域仅为其中的一段弧长，故若模型中选取整个天轮进行分析会增加划分网格时的单元和节点个数，从而延长了分析时间，因此仅提取天轮作用的有效区域，切除天轮无用的部分。将钢丝绳两端同时施加拉力，使得钢丝绳和天轮形成弯曲的弧形接触。

图1 钢丝绳弯曲缠绕模型简化示意图Fig.1 Wire rope wrapping model simplified diagram

本文的仿真研究对象为1+6型钢丝绳，具体参数见表1。根据2016年煤矿安全规程（国家安全监管总局87号令）第四百一十九条，选用天轮直径与钢丝绳直径的比值必须大于等于80，以此来确定天轮直径。

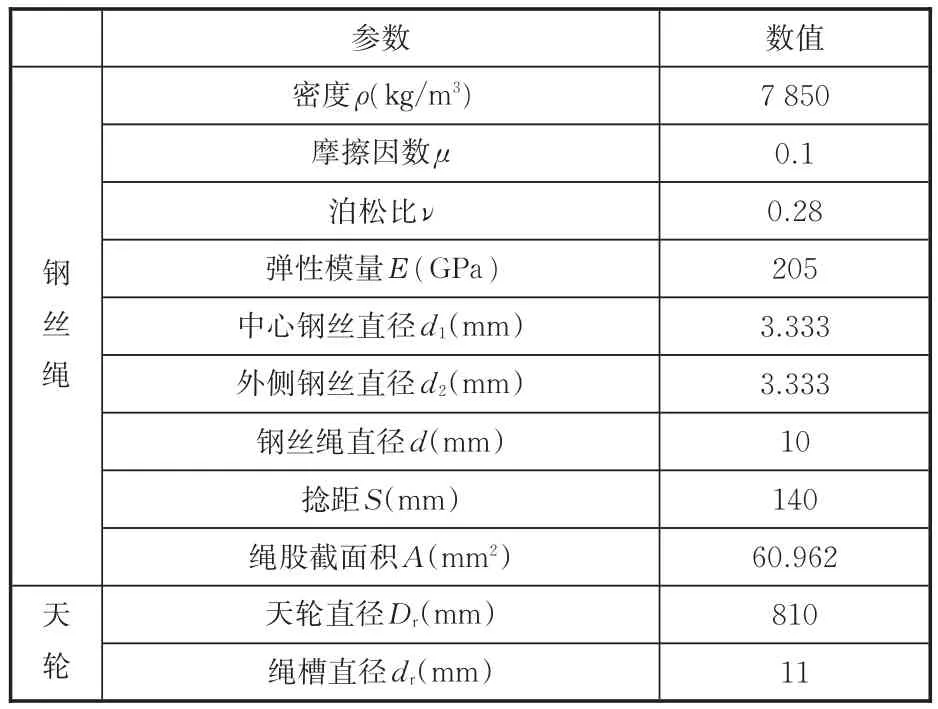
表1 1+6型钢丝绳及天轮主要技术参数Tab.1 The main technical parameters of 1+6 type wire rope and sheave

为了得到更加精确的计算结果，将重复绘制不同包角下钢丝绳的弯曲模型。钢丝绳中心丝中心线的轨迹可以视为一个简化的螺旋线，其x轴的螺旋角为0，在笛卡儿坐标系中用矢量形式表示为

式中，Rr为天轮半径；θr为钢丝绳和天轮的包角。

钢丝绳的各个外丝可以视为一个二次螺旋线，其中心丝中心线的表达式如下：

式中，Rco为侧丝中心线的螺旋半径；αsj为第j根侧丝的初始相位角；βco为侧丝中心线的螺旋角。

在CATIA的草图中绘制中心钢丝截面圆，然后通过扫掠命令生成中心钢丝实体，并通过式（2）绘制侧丝中心线，以侧丝端点处法平面绘制侧丝截面圆，沿侧丝中心线扫掠生成侧丝实体，再按上述步骤依次生成其余5根侧丝。重复上述步骤，绘制包角133°～180°上的实体模型。

1.2 有限元模型的建立

将生成的模型导入ABAQUS中，进行设置建立有限元模型。定义中心钢丝与外侧钢丝之间、外侧相邻钢丝之间、外侧钢丝与天轮之间均为摩擦接触。定义单元类型为C3D8R八节点线性六面体单元，并对钢丝绳进行网格划分。钢丝绳两端端面分别耦合到端面中心参考点上。两端均以端面法向为y轴建立局部坐标系，限制参考点在x、z方向上的移动自由度和旋转自由度，由于钢丝绳在受载过程中本身会发生旋转，所以不能限制在y方向上的旋转自由度，同时施加集中力F=10 kN。将天轮设置为刚体，天轮的圆心为参考点进行耦合。以全局坐标系为基准，限制天轮在x、y和z方向上的移动自由度及在y、z方向上的旋转自由度，仅留下天轮轴向的旋转自由度，以模拟天轮实际的运转情况。生成的有限元模型见图2。

图2 钢丝绳有限元模型Fig.2 The finite element model of wire rope

在后处理过程中，通过free body cut指令得到沿钢丝绳中心丝的轴线方向各个断面的张力，用上述方法得到弯曲绳股中各丝沿其轴线方向张力的分布值。为了更好地表述，对钢丝绳股内各钢丝进行编号，如图3所示。

图3 钢丝绳各丝编号示意图Fig.3 Numbers in wire rope

2 绳股弯曲张力与包角关系分析

2.1 钢丝绳各丝张力分布

为了对比钢丝绳在弯曲拉伸状态下与直线受拉状态下钢丝张力的分布，先对一个直线段的钢丝绳进行拉伸，边界条件为固定其中一端，另一端约束除轴线方向的旋转自由度和移动自由度以外的所有自由度。

直线拉伸时绳股内各丝张力分布见图4，可以看出，当钢丝绳只承受拉伸载荷而不承受弯曲载荷时，中心丝承受的张力值最大，平均张力值为1 790 N。6根侧丝的张力最大值为1 380 N，张力最小值为1 366 N，张力的差值为14 N，平均张力值为1 369 N。中心丝的平均张力值比侧丝的平均张力值大30.7%。但在同一截面内，6根侧钢丝张力值相差仅为2 N，因此可认为各侧丝的张力几乎相同，张力曲线在同一水平直线上。

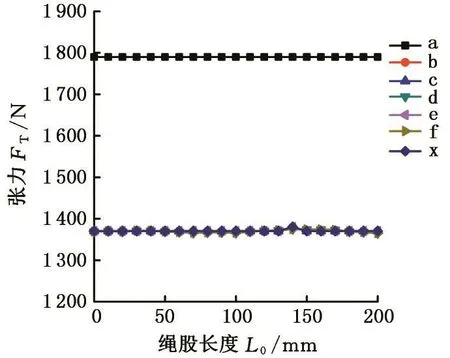
图4 直线拉伸时绳股内各丝张力分布Fig.4 The tension distribution in the strands in the straight stretching process

对钢丝绳绕经天轮弯曲承载且在不同包角下的各丝张力分布进行仿真分析，钢丝绳施加轴向载荷仍为10 kN。钢丝绳在不同包角下各丝张力分布见图5。以过天轮圆心的纵垂面为基准，沿弯曲钢丝绳径向进行等角度切割求出各丝张力，如图6所示。

钢丝绳与天轮的包角发生变化可以理解为钢丝绳与天轮的接触弧长（以下简称“接触弧长”）发生变化，接触弧长的计算表达式如下：

对比图4和图5可以看出，钢丝绳在弯曲之后中心钢丝内张力有明显的变化。同时，处于不同位置的外侧钢丝张力曲线出现明显的离散分层现象。

为了更加清楚地分析包角变化对钢丝绳内各丝张力的影响，下面分步对比分析图5中各个分图。

（1）包角度数为133°时，即接触弧长为940 mm，接触弧长与捻距比值为6.71，此时钢丝绳内各个侧丝张力与直线受拉状态下的张力相比，发生了较大差异，同一截面的张力差由原来的2 N迅速增大至80 N。

（2）包角度数增大至137°时，即接触弧长为968 mm，接触弧长与捻距比值为6.91，各个外层钢丝的张力分布曲线明显向中间集中，出现了大面积交叉的现象，同一截面的张力平均最大差值由80 N变化至54 N。

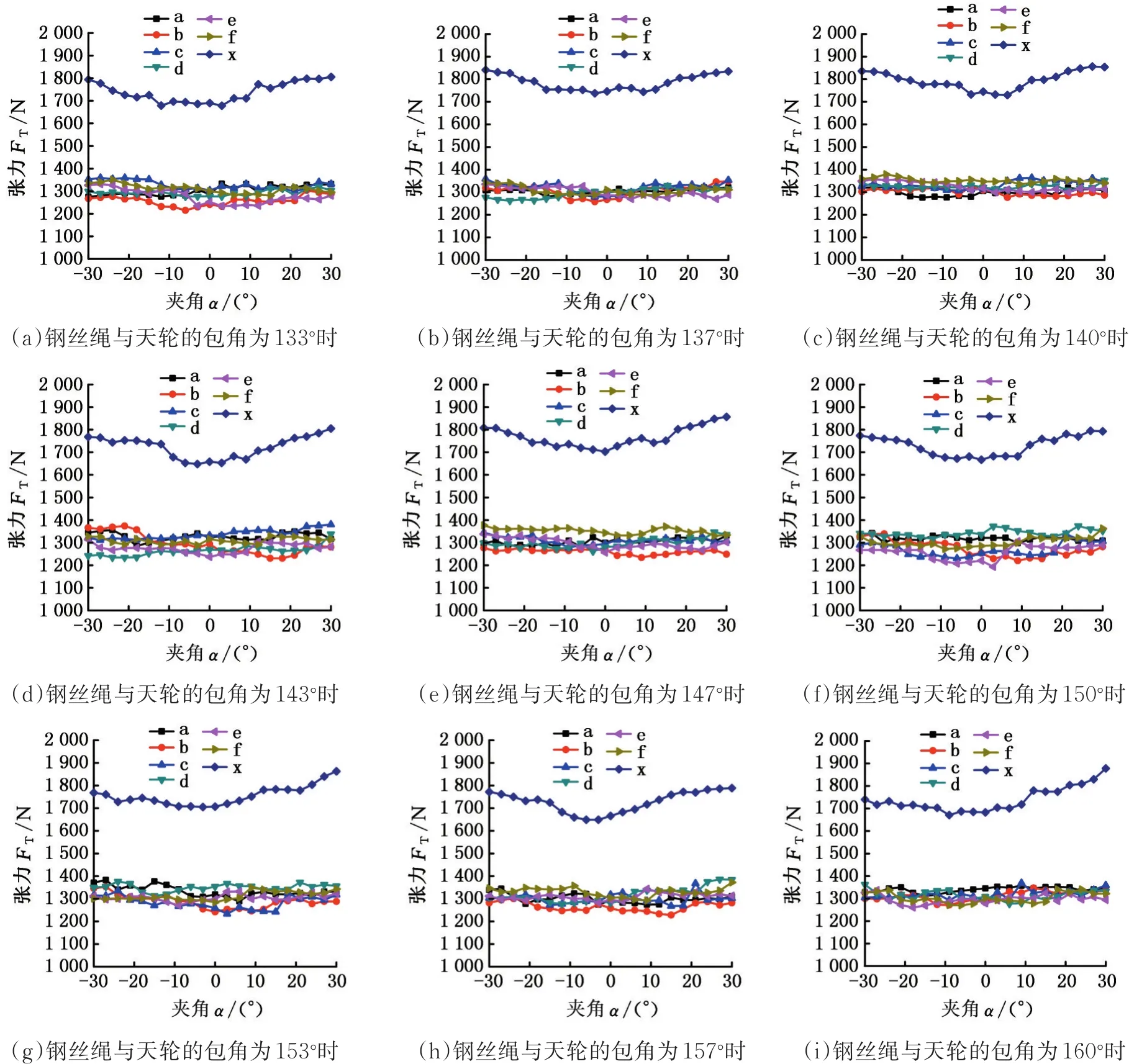
图5 钢丝绳在不同包角下各丝张力分布Fig.5 The tension distribution of steel wire under different package angles

图6 切割平面示意图Fig.6 Cutting plane diagram

（3）包角度数增大至150°时，即接触弧长为1 060 mm，接触弧长与捻距比值为7.57时，外侧钢丝张力分布曲线开始向两侧分散，曲线发生了明显的分层现象，同一截面的张力平均最大差值由54 N变化至111 N。

（4）包角度数增大至160°时，即接触弧长为1 130 mm，接触弧长与捻距比值为8.07，外侧钢丝张力分布曲线又开始向中间集中，多组钢丝对应的张力分布曲线再次发生大面积交叉的现象，同一截面的张力平均最大差值由111 N变化至60 N。

（5）图5各个分图中，中心丝张力的曲线总是中间偏低两侧偏高，这主要是钢丝绳与天轮之间的摩擦力造成的。

由此可知，钢丝绳在不同包角下发生弯曲拉伸时，各丝张力分布有较大的差异。当包角度数从133°增大至137°，外侧钢丝的张力曲线分布由分散分布过渡到集中分布；由137°增大至153°时，外侧钢丝的张力曲线由集中分布过渡到分散分布；最终包角增大至160°，外侧钢丝的张力曲线再次变化为集中分布。据此可知，侧钢丝的张力曲线分布经历了周期性的变化规律：由分散到集中再到分散再到集中。

2.2 张力差值与接触弧长间的关系

为了更加明确地分析钢丝绳各丝张力的差值变化，从图5中提取各个包角下张力的最大值和最小值，并计算出侧丝的张力变化差值，绘制侧丝张力差值随接触弧长与捻距比值的变化关系图，见图7。

图7 张力差值与接触弧长关系（仿真）Fig.7 Relationship between tension difference and contact arc length（simulation）

图7 中，纵坐标代表张力分布的集中程度，其数值越小，表示各丝之间的张力差值较小；数值越大，则表示各丝之间的张力差值较大。从图7中可以看出，张力差值的变化呈周期性变化，当接触弧长为钢丝绳捻距一半的偶数倍时，钢丝绳中各丝的张力差值较小；接触弧长为钢丝绳捻距一半的奇数倍时，张力差值较大。

3 钢丝绳弯曲张力分布规律实验验证

3.1 实验及原理方案

搭建图8所示的实验装置，钢丝绳分为三段，左右两侧均为牵引钢丝绳，中间段为实验钢丝绳，通过两个拉力传感器与牵引钢丝绳连接。左侧牵引钢丝绳缠绕在卷筒3上，通过压板进行固定。右侧牵引钢丝绳通过钢丝绳夹固定在固定销轴9上。通过调节左滑轮4和右滑轮8的位置，改变天轮与钢丝绳之间的包角大小。在钢丝绳上粘贴光纤布拉格光栅（fiber bragg grating，FBG）传感器测量各丝发生的应变。

图8 实验台模型Fig.8 Experiment table model

实际工况中，钢丝绳与天轮的包角多在140°～190°范围内。如中信重工国家安全生产洛阳矿山机械检测中心的多绳缠绕式提升机试验平台的包角约为140°，多绳摩擦式提升机的包角多在180°～190°范围内。为方便计算，实验时选择包角最大度数为180°，同时选取最小度数为157.7°，此时实验所用钢丝绳-天轮接触弧长变化范围大于一个钢丝绳捻距，更加容易验证前文所述的规律。

测量系统主要由宽谱光源、光环形器和多个FBG串联而成的传感器组成，其工作原理见图9，可以看出，FBG传感器经光环行器接受光源入射来的光，反射布拉格条件波长的光，并将被测的应变信号转换成光信号输出；输出的光信号经过光环行器传递给波长解调模块，转换为数字量的波长信号供监测计算机采集，再经过数据处理转化为实际的应变数值。

图9 FBG传感器测量原理示意图Fig.9 Fiber bragg grating sensor measurement principle diagram

实验段钢丝绳上粘贴有4个通道共计28根FBG传感器，将其中24根粘贴在钢丝绳上，每个通道的最后1根FBG传感器作为温度补偿，悬空放置。其中3个通道的FBG传感器刚好构成了一个捻距，见图10。以A4.1、A2.1、A3.1为例进行说明，其代号表明第A根钢丝上共粘贴了3根FBG传感器，依次为第4通道第1根FBG传感器，第2通道第1根FBG传感器，第3通道第1根FBG传感器。第1通道作为补偿误差和验证数据使用，并未在图中显示。

图10 FBG光纤传感器粘贴图Fig.10 FBG fiber sensor paste

3.2 实验过程

实验台及测试系统见图11，实验钢丝绳和天轮的主要参数见表1。实验步骤如下：①通过手轮卸载拉力，待测量软件中显示的FBG传感器波峰数值稳定后，记下各个数值及拉力传感器数值作为初始标定。②加载拉力至指定数值，本次实验设置为10 kN，通过天轮左侧拉力传感器读出，待稳定后记下各个FBG波峰值及天轮左侧拉力传感器的值。由于天轮随钢丝绳的移动而转动，故此时天轮左右两侧拉力传感器的差值接近零。③移动左右两侧滑轮，改变钢丝绳与天轮的包角大小，重复上述步骤，记录各个传感器显示数值。④重复实验12组，实验次序及钢丝绳与天轮包角值见表2。

图11 实验装置及测试系统（处于初始标定状态）Fig.11 Experimental device and test system（in initial calibration state）

表2 实验次序对应钢丝绳与天轮包角值Tab.2 The order corresponding to the wire rope and sheave angle value

计算得到FBG传感器中心波长漂移量（nm）：

式中，Λ为光栅周期；ΔΛ为光栅周期的变化量；neff为光纤纤芯的有效折射率；Δneff为有效折射率的变化量；ε为被测物体应变；ΔT为被测物体温度变化量；Pe有效弹光系数；α为热膨胀系数；ξ为热光系数；Kε为应变灵敏度系数，即单位微应变时光纤光栅的波长漂移量；KT为温度灵敏度系数。

对于1 462～1 618 nm系列的光栅，取Kε=1.2 pm，KT=10 pm/K。

当FBG传感器不受温度作用时，可将其视为应变传感器；当FBG传感器只受温度作用时，可将其视为温度传感器。每个通道的最后1个FBG传感器不受载荷作用，而只受环境温度的影响，故有

式中，Δλ1为仅受温度影响的FBG传感器中心波长的漂移量。

钢丝绳上的其余FBG传感器由于既受载荷的作用，又受环境温度的影响，故有

式中，∆λ2为受温度和载荷影响的FBG传感器中心波长的漂移量。

联立式（9）和式（10），即可求得钢丝绳的应变：

3.3 实验结论

通过计算可得到各丝张力随包角的变化情况，提取张力中的最大值与最小值，绘制侧丝张力差值随接触弧长与捻距比值的变化关系，见图12。

图12 张力差值与接触弧长关系（实验）Fig.12 Relationship between tension difference and contact arc length（experiment）

从图12中可以看出，接触弧长与捻距比值变化至7.85～7.98附近时，张力差值迅速减小。当比值再次增大时，张力差值也发生瞬间改变，开始增大。当比值变化至8.45附近时，张力差值斜率开始减缓，同时达到最大值。随着比值的继续增大，张力差值又开始减小，当比值接近8.87时，张力差值达到最小值，并有再次增大的趋势。

钢丝绳在受到拉伸载荷时，根据材料特性及其缠绕的结构，捻距会略微变长。在有限元仿真过程中，由于每次仿真都会重新计算钢丝绳长度，因此这种现象并不明显，但在实验中却明显可发现原结论中的比值总是偏小，这种情况是合理的。

由图12可知，当接触弧长为钢丝绳捻距一半的奇数倍时，即两者比值为8.5附近时，钢丝绳中张力差值最大；当接触弧长为钢丝绳捻距一半的偶数倍时，即两者比值接近8.0和9.0时，钢丝绳中张力差值近似最小。除去由于实验条件限制所造成的误差，该规律与仿真结果基本吻合。

3.4 结果分析

仿真和实验的结果都揭示了同样的规律，但为了更加精确地分析其结果，运用灰色系统理论方法对仿真和实验的结果进行比较分析。

灰色关联分析是灰色系统理论中一个重要分支，其基本思想是根据曲线几何形状的相似程度来判断不同序列之间的联系紧密程度，其折线的几何形状越接近，相应序列之间的关联度就越大，反之则越小［16］。且其对于样本量的多少和样本有无明显规律均同样适用，这正好符合本研究分析的需求，因此本文采用灰色关联分析中的灰色综合关联度来对仿真和实验的结果进行分析。

从图7中的仿真结果提取各点数据，有

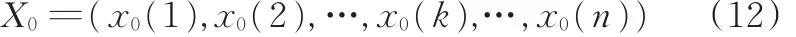
从图12中的实验结果提取各点数据，有

由于仿真数据与实验数据的个数不相同，必须将X0与X1化为等时距序列，去除两者多余的数据，于是

为了求解综合关联度，首先需要计算绝对关联度，求X0和X1的始点零像化，得

计算X0和X1的灰色绝对关联度为

其次计算相对关联度，求初值像：

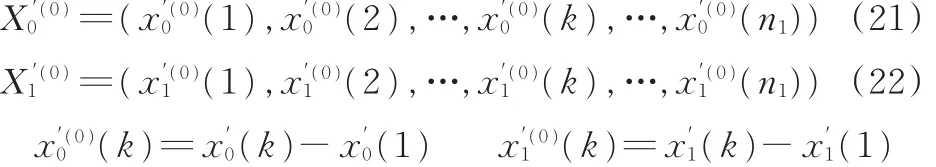
最后计算灰色综合关联度：

其中，θ为系数，是权衡两个序列绝对量和变化速率之间的重要指标，在此视两者同等重要，取θ=0.5［16］。经过式（18）、式（23）和式（24）的计算，得到了仿真数据和实验数据的关联度值，ε01=0.82，r01=0.75，ρ01=0.78。

灰色绝对关联度（0＜ε01≤1）只与两组数据的几何形状相关，即仿真数据和实验数据在几何上的相似度越大，ε01的值越大。ε01=0.82代表虽然有一些的误差，但两组数据在几何上近乎高度的相似，产生误差的因素有许多，最大的因素是两组数据的长度不一致所造成的。

灰色相对关联度（0＜r01≤1）只与两组数据的相对于始点的变化速率有关，而与各个观测值的大小无关，即仿真数据和实验数据相对于始点的变化速率越趋近于一致，r01的值越大。r01=0.75代表在变化速率上两者有较大的误差，产生误差的因素主要是由于进行仿真时每次变换包角大小均需要重新建模，工序过于繁杂，所以无法更为精细地划分包角变化的数值，而样本过少，张力差值的斜率变化过快，从而影响曲线的变化速率，导致相对关联度值较小。

灰色综合关联度（0＜ρ01≤1）既反映了两者折线的相似程度，又反映了两者相对于始点变化速率的接近程度，是较为全面反映序列之间联系是否紧密的一个数量指标。通过ρ01=0.78可以看出两者还是有很大的相似性，造成数值偏小的因素除了上述两个方面外，还有仿真和实验时钢丝绳和天轮的摩擦因子存在差异，实验时施加力的大小不够精确等因素。

综上所述，尽管只有一组实验数据印证了仿真结果，但通过灰色综合关联度分析可推导出其他包角时的仿真结果也与实验结果基本符合，即钢丝绳绕过天轮或滑轮时各丝张力的变化规律成立。

4 结论

（1）钢丝绳绕经天轮弯曲时，绳股中各丝张力出现较大差异，且各个侧丝的平均张力随接触弧长呈现周期性的变化，即接触弧长为钢丝绳捻距一半的偶数倍时，绳股内钢丝张力差较小；当接触弧长等于钢丝绳捻距一半的奇数倍时，绳股内钢丝张力差较大。

（2）在提升机设计过程中，应考虑钢丝绳与天轮、滑轮等的接触弧长对钢丝绳使用寿命的影响。当接触弧长为捻距一半的偶数倍时，绳内各丝张力分布较集中，张力差值较小，能有效延长钢丝绳的使用寿命。

（3）需要指出的是本论文仅以直径为10 mm的1+6型钢丝绳为例作了仿真和实验分析，但钢丝绳弯曲张力这一变化规律对其他类型的钢丝绳在弯曲承载时是否成立，尚需大量的实验予以验证。