基于均匀化循环理论的车身焊点布局优化方法

胡朝辉 崔雪姣 成艾国 秦晓凯

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

车身结构是由许多复杂的薄板件焊接而成的，典型的车身结构中通常有3 000～5 000个焊点，在一条生产线中平均每减少一个点焊的装置，就可以节约大概3万美元成本［1］。然而传统的焊点布置方式以经验为主，可能造成焊点分布不均，从而造成成本增加或车身结构强度不足。总之，焊点的布置不仅与制造成本有关，而且对整个结构的刚度、强度和NVH等性能也有着重要的影响，所以通过优化使得焊点得到合理的布置具有重要的意义。

国内外学者对焊接结构的研究中，涉及焊点的布局对结构刚度、强度等性能影响的有很多。BHATTI等［2］提出了一种优化程序可以基于决策指示增加和删除焊点，并制定了一个鲁棒性指标来描述损坏或失效的焊点个数对系统性能的影响，并将提出的方法应用在某汽车白车身结构上，在综合考虑制造成本和结构性能的前提下优化焊点的数目。ERTAS等［3］提出了一种基于疲劳寿命的优化方法，可以找到焊点布置的最佳方案和板件搭接的最佳长度。张守元等［4］采用拓扑优化的方法对某商用车驾驶室白车身的焊点布局进行了优化，并在不减少焊点数量的前提下提高了车身的刚度。吕毅宁等［5］针对某紧凑型两厢轿车，基于不同区域对车身结构相关性能的不同影响，将车身划分成多个设计区域，利用拓扑优化的方法对其进行分级优化，并通过某车身中焊点布局的设计验证了提出方法的可行性与有效性。刘子辉［6］基于焊点应变能密度采用拓扑优化的方法对某商用车驾驶室白车身的焊点布置方案进行了优化，在保证相关性能的前提下减少了焊点数目，并且得到了更好的焊点布置鲁棒性。陈勇［7］基于应变对某轿车B柱焊点进行疲劳寿命预测，进而根据预测结果选择合理的焊点布置优化方案，并用曲线拟合了焊点间距和疲劳寿命之间的关系。

由于保证焊点质量的过程是一个综合、复杂的过程，易受焊接参数、工艺规范等因素的影响，因此本文不考虑焊点质量的因素，仅考虑焊点位置的布局方式，提出了一种焊点布局优化方法。首先通过均匀分配原理确定接头焊接边焊点的配比形式；然后建立关键接头均布焊点优化问题的数学模型；最后通过焊点循环迭代原理确定焊点基于等间距分布的迭代形式，以白车身刚度和车身各个关键区域最大应力为约束，以焊点数量最小为设计目标。

1 车身结构焊点布置的优化方法

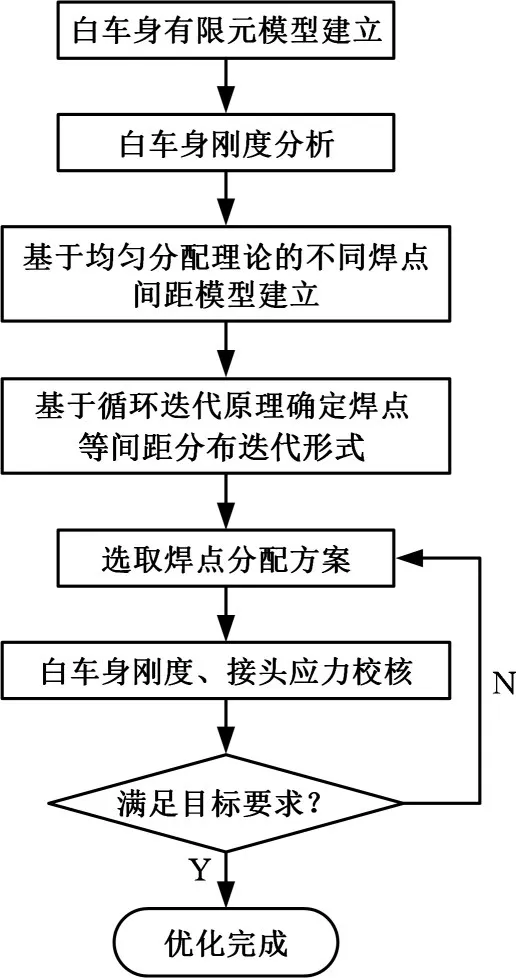
图1 焊点布置优化流程图Fig.1 Flow chart for optimization of welding spot

国内关于焊点布置的研究，只针对性地解决了车身多余焊点数量的减少问题。其中，拓扑优化分析结果是以值为0～1单元密度的大小表征焊点的重要程度，转化成实际工程应用的过程中，存在不确定性，同时无法进行焊点数量、间距及焊点经济性三重控制。针对该问题，本文提出了基于焊点均匀布置的车身接头焊点布置优化设计方法，如图1所示，主要包括以下4个步骤：①建立精确的白车身有限元模型，该模型主要包括前后车架、前后地板、前隔板、左右侧围、前舱、顶盖总成等；②基于焊点均匀分配理论，对白车身各接头焊接边的焊点个数进行分配；③基于焊点循环迭代原理，确定白车身各接头焊接边焊点的迭代形式，并对不同焊点间距进行分析求解；④以白车身刚度和车身各个关键区域最大应力为约束，以焊点数量最小为设计目标进行焊点布置优化。最后对优化前后车身结构的性能及焊点数量进行对比分析。

2 焊点布置方法

焊点对于整个结构的强度、刚度、低阶固有模态频率等动静态性能具有很大影响。从生产成本来说，不合理的焊点布置会导致焊点数量增加，增加焊接装配成本，从力学角度来说，焊点附近存在着严重的应力集中，容易产生疲劳裂纹；因此，在早期设计中对焊点进行优化布置对于提高车身结构的综合性能和降低焊接装配成本具有重要意义。

2.1 焊点均匀分配原理

本文提出的焊点布置的优化设计是针对复杂系统关键接头的优化设计问题提出的。在白车身详细设计阶段之前，优先寻找白车身骨架最为敏感的区域，对这些关键区域设定合理的参考设计域，并对参考设计域内的焊点布置进行优化设计，对提高车身结构性能有重要影响。

为了降低焊点布置的优化设计问题的难度，提高优化设计结果的工程实用价值，本文提出一种新的车身结构焊点布置的方法，即焊点均匀化循环分配方法。假设某车型包含I个接头，其中每个接头包含mi（i=1，2，…，I）个焊点，且每个接头包含K条焊接边，每条焊接边包含nik（k=1，2，…，K）个焊点。将接头的各个焊接边分配从1到K的标码编号（定义某个接头的任意一条焊接边为编号1，编码顺序按照顺时针顺序编排）。根据以上假设，图2所示接头每条焊接边焊点总数分别为ni1、ni2、ni3，该接头包含的焊点数为mi，因此，接头焊点总数mi=ni1+ni2+ni3，则接头i焊点总数mi与各焊边焊点数关系式如下：

当mi=1,4,…,3q-2时，

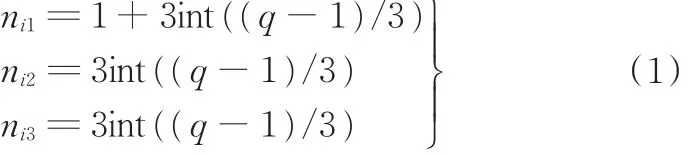
当mi=2,5,…,3q-1时，

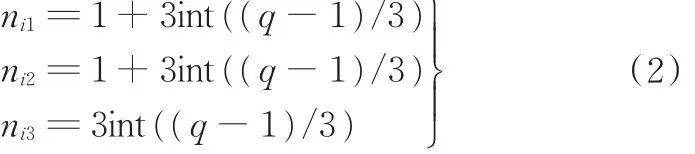
当mi=3,6,…,3q时，

式中，q为等差数列的项数；int（）为取整函数。

图2 某接头区域焊点循环分配示意图Fig.2 The loop distribution for one joint area

根据循环分配公式可得到接头i焊点总数mi与各焊边焊点数的关系，如表1所示。

表1 某接头焊点总数与每条边焊点个数的关系Tab.1 The relationship between the total number of spot weld and the number on each side

根据焊点循环分配原理，图2所示接头焊点分布规律如下：当接头焊点总数为1时，第1条焊接边焊点数为1，第2条焊接边焊点数为0，第3条焊接边焊点数为0；当接头焊点总数为2时，第1条焊接边焊点数为1，第2条焊接边焊点数为1，第3条焊接边焊点数为0；当接头焊点总数为3时，第1条焊接边焊点数为1，第2条焊接边焊点数为1，第3条焊接边焊点数为1，以此类推。

2.2 焊点循环迭代原理

构件翻边纵向中心线被称为焊接线，焊点位置由焊接线的长度及焊接线上的焊点间距决定。图3所示为焊点建立实例，根据焊接线长度建立焊点信息，直至得到最小有效焊点间距，即可确定焊点的个数和位置。在实际生产中，设置焊点布置中的最小间距为30 mm。假设图3中每条焊接边最后一次建立焊点时的焊点间距即为最小间距，则图示接头焊点模型建立完成。

依据循环分配原理，定义第i个接头焊点编号为1，2，…，qi。通过改变每组焊点的弹性模量来改变接头模型中焊点的个数，即设置本次参与优化的焊点组弹性模量E为210 GPa，其余焊点的弹性模量都为0.1 kPa。由于焊点个数在迭代过程中是不断变化的，这样在后续的每次迭代过程中就可以实现具有不同焊点信息的有限元模型的重建。

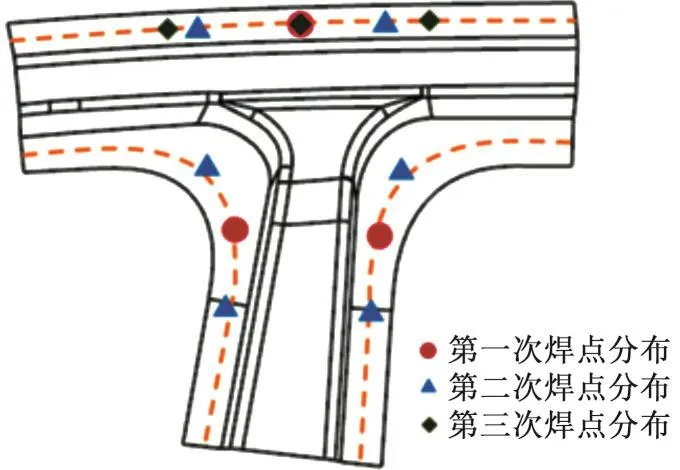
图3 某接头区域焊点编号示意图Fig.3 The number of spot weld for one joint area

2.3 焊点优化数学模型

车身结构是一个整体焊接结构系统，关键区域的焊点数量和布局对车身结构的性能具有重要影响，并且不合理的焊点布置会使焊点数量增加，通过优化焊点布置方案可以提高车身结构的综合性能并降低焊接装配成本。

本文以关键接头区域焊点总数为目标函数，以车身性能为约束函数，以单个接头区域焊点数量为设计变量，其数学模型可以表示为

式中，S(mi)为目标函数；g(mi)为约束函数；mi为设计变量；为设计变量的下限；为设计变量的上限。

3 应用实例

本文采用某量产车型白车身模型对建立的数学模型进行验证，如图4所示，模型总质量为316 kg，单元个数为456 002，节点个数为474 776，四边形单元数为441 387，三角形单元数为11 230，三角形单元占比2.4%，满足仿真要求。

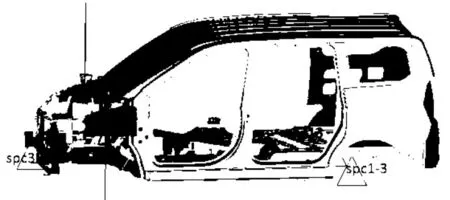
图4 某车白车身有限元模型Fig.4 The finite element model of white body

3.1 基于焊点循环分配原理及均匀迭代原理的焊点模型建立

本文将16个接头区域（A柱上接头区域、A柱下接头区域、B柱上接头区域、B柱下接头区域、C柱上接头区域、C柱下接头区域、D柱上接头区域、D柱下接头区域）分离出来，进行基于循环分配原理及均匀迭代原理的焊点模型的建立。鉴于左右对称，只分析同侧8个接头。

以B柱上接头为例（图5）说明焊点模型的建立。沿B柱上接头翻边中心处为焊接线，建立焊点信息。当焊点间距为30 mm时，每条边焊点模型建立完成。图5中所示三条焊接边上五边形即为间距为30 mm的焊点型。

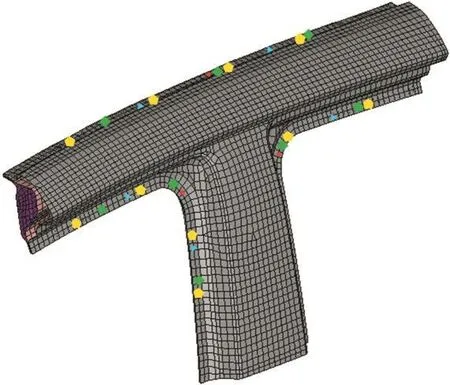
图5 某接头区域焊点模型建立示意图Fig.5 The building spot weld model for one joint area

3.2 分析工况

工况一：白车身扭转刚度。扭转刚度是评价白车身性能的一个重要整体性能指标，反映的是白车身抵抗扭转变形的能力，是整车在过坑、路面不平整等恶劣工况下整车抵抗变形能力的重要参考指标。

工况二：白车身强度分析。本文白车身强度分析重点关注在特定加载工况下车身各个关键区域的最大应力值。白车身接头区域焊点数量不同，将导致在特定加载工况下白车身各接头区域的应力分布趋势发生变化。本文以白车身过坑扭转时车身关键区域（C柱上接头区域、C柱下接头区域、D柱上接头区域、D柱下接头区域）的最大应力值来评价白车身强度情况。有限元模型中，先建立各个关键区域单元的set集（应包含整个接头区域），然后以各set集的最大应力来作为白车身强度分析的评价指标。

3.3 焊点优化数学模型

为了实现车身接头区域焊点优化，本文将白车身同侧的8个接头焊点数作为设计变量，分别用m1、m2、…、m8表示。白车身初始状态下的焊点数量分别为21、25、42、42、42、22、14、14，初始扭转刚度值为11 580 N·m/（°）。将扭转刚度以及关键接头区域最大应力作为约束条件，按照式（4）得到接头焊点优化的数学模型如下：

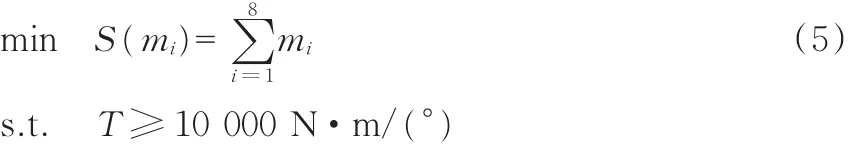
式中，S(mi)为8个接头区域焊点数总和；T为扭转刚度；σ1、σ2、σ3、σ4分别为工况二中车身关键控制区域的最大应力。

3.4 优化结果

经过多次迭代之后，提取优化结果，部分优化结果如表2所示。优化后A柱上接头区域、A柱下接头区域、B柱上接头区域、B柱下接头区域、C柱上接头区域、C柱下接头区域、D柱上接头区域、D柱下接头区域焊点总数分别为15、18、28、26、38、18、10、10。根据焊点循环迭代原理，得到各个接头每条边的焊点分配情况，例如B柱上接头区域总焊点数是28。根据焊点优化方案，对白车身扭转刚度和应力情况进行对比分析，结果表明白车身扭转刚度较优化前有所增大，如图6（优化前）、图7（优化后）所示；同时，优化后各接头区域结构的最大应力较优化前最大应力略有减小，均满足强度要求，以D柱上接头为例，图8、图9所示为优化前后D柱上接头应力云图。

表2 接头焊点优化结果Tab.2 Result of spot weld in joint

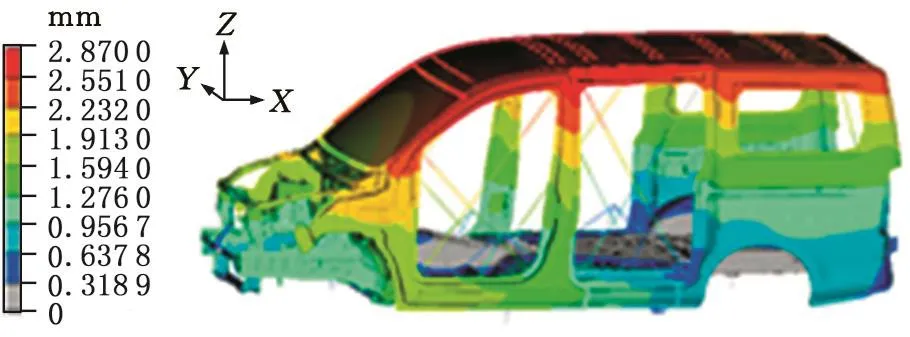
图6 扭转工况白车身位移云图（优化前）Fig.6 The white body displacement in torsional condition（before optimization）

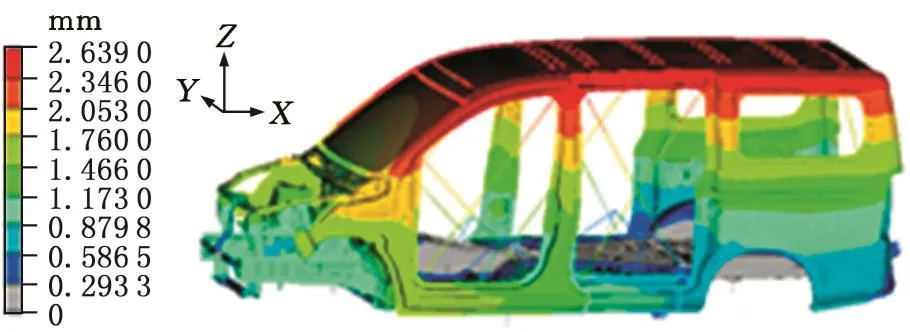
图7 扭转工况白车身位移云图（优化后）Fig.7 The white body displacement in torsional condition（after optimization）

图8 D柱上接头应力云图（优化前）Fig.8 Stress cloud map for D pillar upper joint（before optimization）

图9 D柱上接头应力云图（优化后）Fig.9 Stress cloud map for D pillar upper joint（after optimization）

优化前后扭转刚度、焊点数量对比如表3所示。优化后焊点总个数为163，与初始值相比减少了59个，即焊点数目减少了26%。扭转刚度虽然减小了5.8%，但仍然在允许的范围内。

表3 优化前后结果对比Tab.3 Comparison of before and after optimization

4 结语

本文采用的是某量产车的白车身，首先对其有限元模型进行了建立和分析，得到初始状态的性能及优化区域焊点数量；其次，根据均匀化循环分配理论对优化区域进行了焊点布置优化；最后对优化前后的性能及焊点数量进行了对比分析。

优化前后通过对比扭转刚度和焊点数量可以得出：焊点数量减少了26%，扭转刚度虽然减小了5.8%，但仍在允许的范围内。

焊点布置对一阶模态频率、刚度、NVH特性和碰撞性等多种性能都有影响。本文在对焊点布置进行优化时只考虑了扭转工况下的刚度和强度，存在一定的局限性，在今后的研究中会综合考虑多种性能，以便得到更加合理的焊点布置方案。