基于响应曲面法的YG8硬质合金刀片化学机械抛光工艺参数优化

袁巨龙 毛美姣 李 敏 刘 舜 吴 锋 胡自化 秦长江

1.湖南大学国家高效磨削工程技术研究中心，长沙，410082

2.湘潭大学复杂轨迹加工工艺及装备教育部工程研究中心，湘潭，411105

3.浙江工业大学特种装备制造与先进加工技术教育部重点实验室，杭州，310014

4.湖南科技大学难加工材料高效精密加工湖南省重点实验室，湘潭，411201

0 引言

我国高速或超高速切削、精密模具制造、纳米加工和微细加工快速发展，对刀具质量的高性能要求日益苛刻［1］。在高速切削过程中，由于刀具的切削区存在剧烈摩擦和高温高压作用，刀具表面粗糙度大的部位易磨损，会严重缩短了刀具寿命［2］，因此，提高硬质合金刀具的表面质量，改善切削过程中的摩擦状态，从而减缓刀具磨损是切削加工亟待解决的问题［3］。

金刚石砂轮磨削加工是目前硬质合金刀具最常用的加工方法，但金刚石砂轮磨削速度快，易导致刀片表面产生热变形、烧伤、裂纹等表面缺陷，极大地降低了刀片性能和缩短刀片寿命［4-5］。化学机械抛光（chemical mechanical polishing，CMP）是一种通过化学腐蚀和机械磨削相结合，从而使得表面达到平滑的工艺。已有学者对硬质合金刀片进行了CMP试验研究，结果表明，与金刚石砂轮磨削加工相比，CMP工艺磨削硬质合金刀片后的表面质量明显更好［6-11］。

确定合适的工艺参数、提高加工效率是CMP应用于硬质合金刀片规模化生产的关键因素。由于CMP过程涉及到摩擦学、化学和流体力学等学科领域，其作用机理非常复杂［12］，导致获得最佳工艺参数存在一定难度，且各工艺参数之间具有交互作用。响应曲面法（response surface methodology，RSM）具有泛化能力强、预测精度高的优点，不仅能采用多元二次回归方程来描述自变量与响应值之间的函数关系，也能反映各变量之间的相互作用关系，因而采用RSM建立预测模型以及进行工艺参数优化不失为解决上述问题的一种有效方法［13-16］。但CMP过程中需要控制的工艺参数有许多，本文只能根据实际加工条件对部分关键影响因素展开讨论。

本文以YG8硬质合金刀片为研究对象，基于单因素试验选取抛光转速n、抛光压力p、磨粒粒径D和磨粒浓度（质量分数）C等4个关键工艺参数的优化区域为自变量的水平，采用中心复合设计（central composite design，CCD）方法设计YG8硬质合金刀片表面加工质量与4个主要工艺参数的试验方案，引入RSM进行方差分析，分别建立材料去除率 RMR（material removal rate，MRR）及CMP加工后刀片表面粗糙度值Ra与4个工艺参数的二阶预测模型，优化YG8硬质合金刀片CMP工艺参数，获取最佳工艺参数，从而实现了YG8硬质合金刀片CMP工艺的表面粗糙度最小化和MRR最大化的目标。

1 试验方法及材料特性

1.1 试验方法

化学机械抛光（CMP）工艺将纳米粒子的机械研磨作用和抛光液的化学腐蚀作用有机结合起来［17］，对工件表面进行超精密加工。YG8硬质合金刀片CMP加工试验原理如图1所示。

图1 试验原理图Fig.1 Experimental principles

抛光盘1由抛光装置上的电机带动旋转轴实现旋转，抛光垫5通过背胶固定在抛光盘上同向旋转，抛光液由抛光液输送装置4控制，并以一定的流速施加到抛光垫表面，通过抛光垫的旋转将抛光液均匀地输送到抛光系统的加工区域，硬质合金刀片2由夹具3固定，并以一定的载荷将硬质合金刀片2压在旋转的抛光垫5上，跟随夹具3旋转。在YG8硬质合金刀片的CMP过程中，抛光液中的氧化剂H2O2将刀片表面氧化，在表面形成一层硬度低于工件硬度的钝化薄膜。抛光盘以一定的压力加载在夹具上，高速旋转时产生的高温使被抛光表面易发生变形，从而形成“加工变质层”，抛光液中游离的磨粒经过机械作用将加工变质层去除，使刀片表面重新裸露，从而再次发生氧化反应。由此，刀片在抛光液化学腐蚀和机械研磨的交替作用下，完成了对其表面的抛光。

材料去除率计算方法如下：

式中，RMR为硬质合金刀片的材料去除率；Δm为CMP前后硬质合金刀片的质量差；ρ为硬质合金刀片的密度；A为硬质合金刀片与抛光垫接触的面积（YG8硬质合金刀片的表面面积为144.43 mm2）；Δt为时间差，取Δt=60min。

刀片抛光前后的质量用精度为0.1 mg的电子秤测量。

抛光垫选用聚氨酯抛光垫（长沙欣辉电子科技有限公司），采用自制的抛光液，主要成分有磨料粒子、腐蚀介质和助剂。抛光液以1 000 mL去离子水为基液，取0.5 g分散剂聚羧酸钠溶解于去离子水中，抛光液的磨粒选用莫氏硬度为9的Al2O3，搅拌均匀后，在100 kHz下超声分散0.5 h，同时将30%的H2O2稀释至与磨粒相同的质量分数，加入抛光液中作为氧化剂，抛光时间为60 min，采用超声波工艺对抛光刀片进行抛光后清洗处理。采用型号为JB-IC的表面粗糙度测试仪（上海泰明光学仪器有限公司）测量工件的表面粗糙度。

1.2 材料特性

选用在金属加工中使用广泛且强度高、抗弯性能和抗冲击抗震性好的YG8硬质合金刀片（株洲钻石切削刀具股份有限公司）作为研究对象，其物理性能见表1。

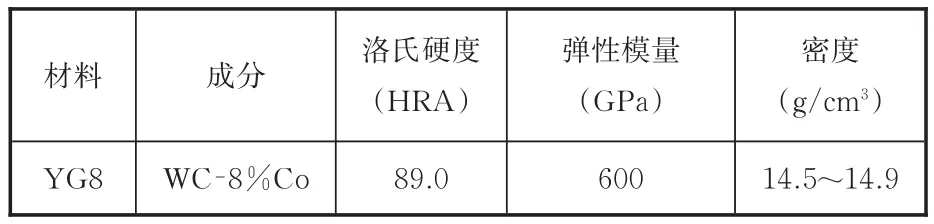
表1 YG8硬质合金刀片物理性能Tab.1 Physical properties of YG8 cemented carbide inserts

2 材料去除率与表面粗糙度预测模型的建立

2.1 工艺参数水平的确定

选取抛光转速、抛光压力、磨粒粒径和磨粒浓度4个关键工艺参数为自变量，通过单因素试验确定自变量的设计域。其他工艺参数不变的条件下，抛光转速、抛光压力、磨粒粒径和磨粒浓度对材料去除率RMR和表面粗糙度Ra的影响试验结果见图2～图5。从图2～图5中可以看出，4个工艺参数对加工效率和加工精度的影响都是显著的，各工艺参数的较优区间如下：磨粒粒径D为1～3 μm，磨粒浓度（质量分数）C为10%～15%，抛光转速n为50～70 r/min，抛光压力p为155.25～258.75 kPa。

图2 磨粒粒径对RMR和Ra的影响Fig.2 Influence of abrasive particle size on RMRand Ra

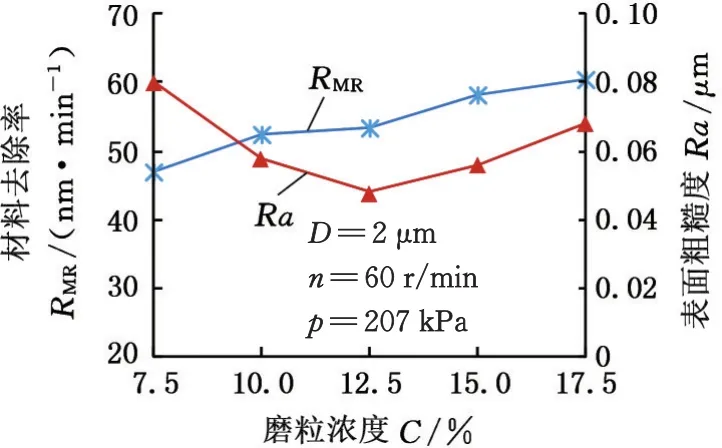
图3 磨粒浓度对RMR和Ra的影响Fig.3 Influence of abrasive concentration on RMRand Ra

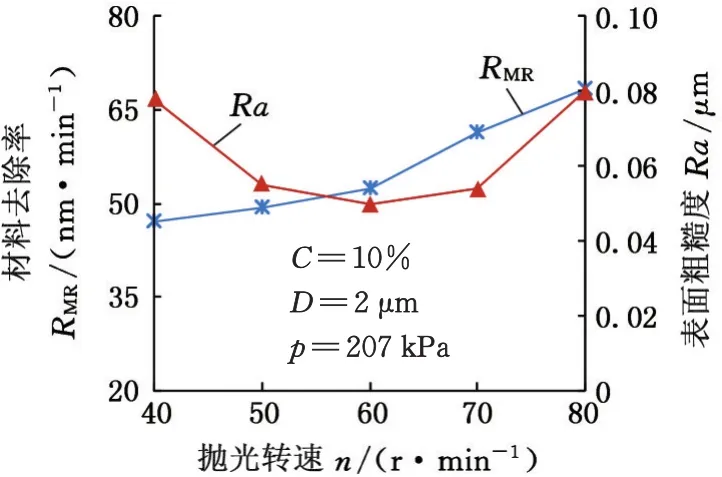
图4 抛光转速对RMR和Ra的影响Fig.4 Influence of polishing rotational speed on RMRand Ra

图5 抛光压力对RMR和Ra的影响Fig.5 Influence of polishing pressure on RMRand Ra

2.2 中心复合设计试验方案与结果

在估计响应曲面时，中心复合设计（CCD）是认可度和应用度最高的试验设计方法，既能评估线性项和交互项，也能估计高阶曲面效应，又能以最少的试验循环次数提供自变量和误差最有效的数据［18］。根据图2～图5的试验结果，采用CCD试验，每个工艺参数选取-1、0和1三个水平，表2列出了CCD试验的4个自变量及其各自的三个水平。

表2 CCD试验因素和水平Tab.2 CCD experimental parameters and levels

表3所示为CCD试验方案及材料去除率RMR和表面粗糙度Ra结果。为减小试验误差，每组试验同时抛光3块刀片，每块刀片随机测量3个点的Ra，再将3块刀片的9个测量值求平均作为每组试验抛光后的Ra有效值，3块刀片测量后计算得到RMR的平均值作为试验的RMR有效值，RMR用式（1）进行计算。

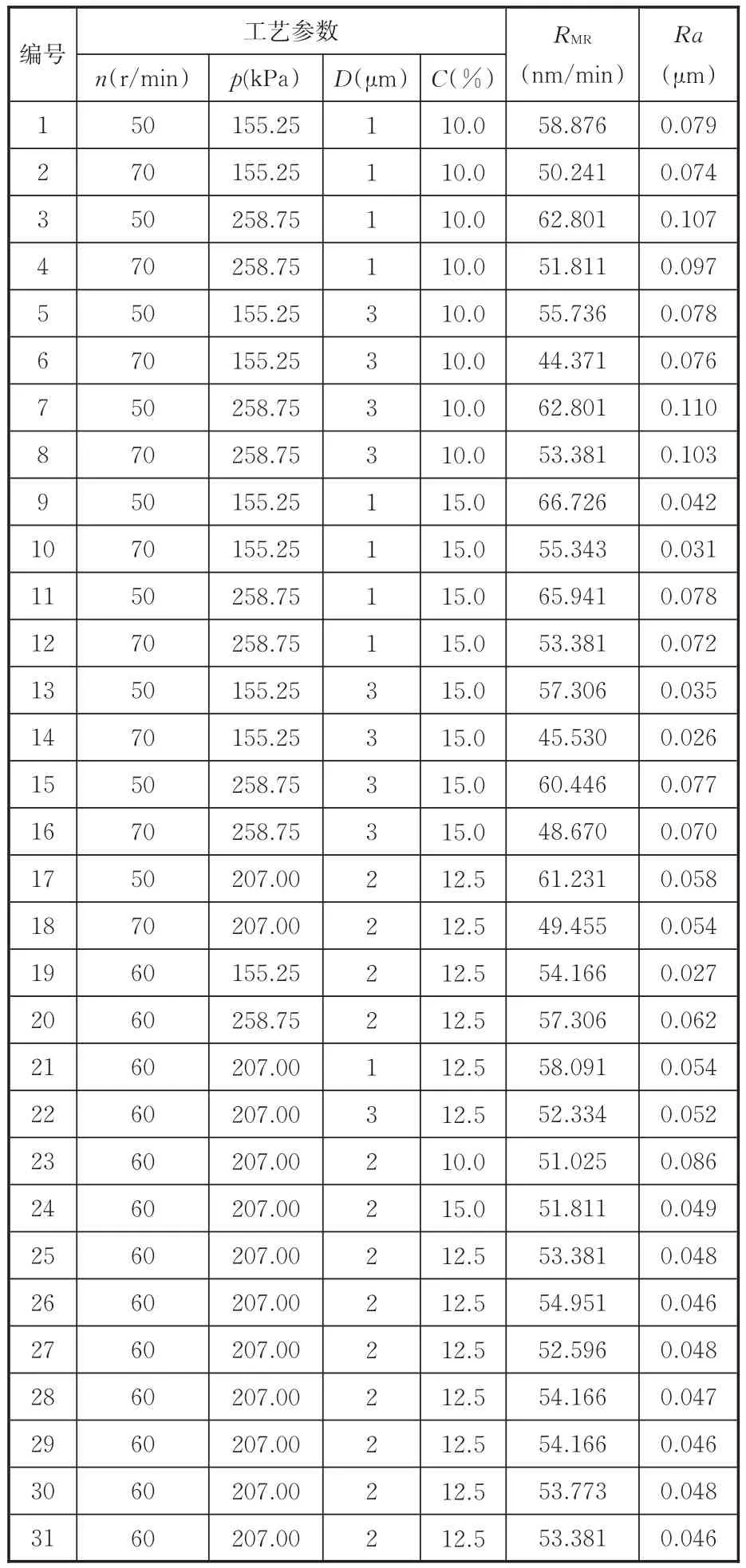
表3 CCD试验方案及试验结果Tab.3 Experimental plan and result based on CCD

2.3 材料去除率与表面粗糙度的预测模型

2.3.1 方差分析

根据表3中的试验数据，基于Minitab对材料去除率RMR和表面粗糙度Ra的结果进行方差分析，检验工艺参数对RMR和Ra的显著性。方差分析结果表明：抛光转速n、抛光压力p和磨粒浓度C 3个因素对RMR和Ra的影响均显著，而磨粒粒径D只对RMR的影响显著；抛光转速n与抛光压力p交互作用（即x1x2）以及抛光转速n和磨粒粒径D交互作用（即x1x3）两项对RMR和Ra的影响均不显著，抛光转速n和磨粒浓度C的交互作用（即x1x4）对Ra的影响不显著，其余各因子交互作用对RMR和Ra的影响均显著，磨粒粒径D对Ra的影响不显著。根据方差分析结果可知，各工艺参数对RMR的影响程度从高到低为：n，D，p,C；对Ra的影响程度从高到低为：C，p，n，D。

2.3.2 模型建立

为找出YG8硬质合金刀片CMP过程中工艺参数与材料除去率RMR、表面粗糙度Ra之间的关系，采用响应曲面法（RSM）对YG8硬质合金刀片CMP过程中工艺参数与RMR及Ra之间的关系进行多元二次方程回归，二阶数学模型如下［19］：

式中，y为响应值；xi、xj为硬质合金刀片CMP过程中工艺参数的数值；β0为常数项系数；βi为线性项系数；βii为二次项系数；βij为交互项系数。

根据方差分析结果，剔除RMR中的不显著交互项x1x2、x1x3和Ra中的不显著交互项x1x2、x1x3、x1x4，建立RMR和Ra与工艺参数之间的多元二阶回归预测模型，表达式分别如下：

2.3.3 模型检验

表4所示为剔除非显著项后对材料去除率RMR的方差分析，其中，DF表示自由度，Adj SS表示调整后的离差平方和，Adj MS表示调整后的均方，F值表示整个拟合方程的显著程度，P值表示不拒绝原假设的程度。RMR回归模型的F=162.58，P＜0.000 1，线性项、平方项和双因子交互项的P值均小于0.05，因此该模型显著，失拟检验（lack-of-fit）的F=0.64＜5.05（95%置信区间为5.05），因此认为模型可信；RMR回归模型的误差占总误差的百分比R2（即多元相关系数）为99.09%，数值大于85%且接近1，调整后的误差占总误差的百分比R2adj（即修正的多元相关系数）为98.48%，数值小于R2且两者数值接近，表明剔除非显著项后模型拟合效果得到了优化。

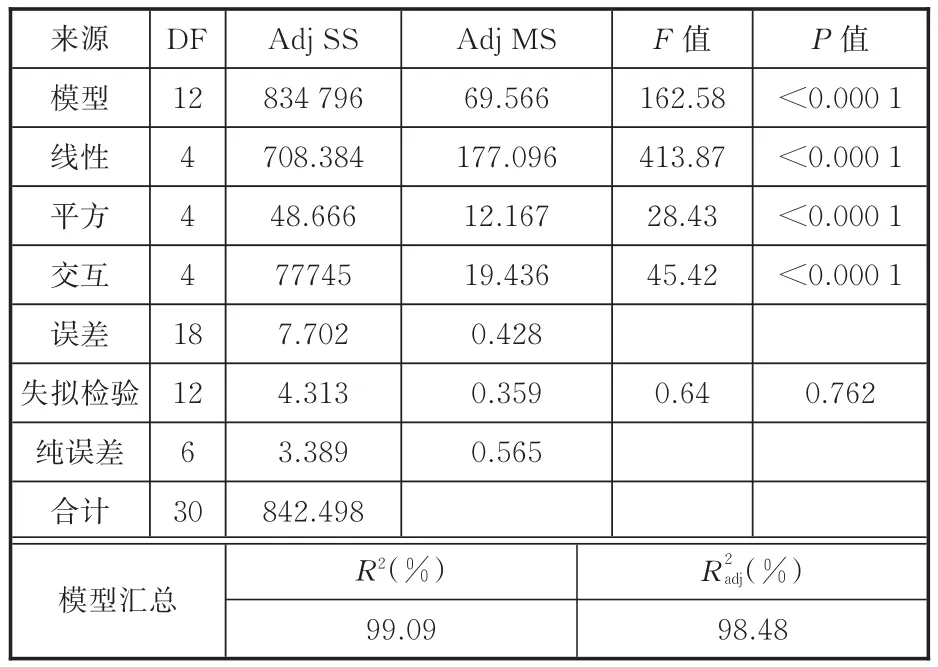
表4 材料去除率模型的方差分析Tab.4 ANOVA for MRR model

表5所示为剔除非显著项后对表面粗糙度Ra的方差分析。Ra回归模型的F=434.21，P＜0.000 1，线性项、平方项和双因子交互项的P值均小于0.05，失拟检验的F=3.31＜5.05，回归模型的误差占总误差的百分比R2为99.60%，调整后误差占总误差的百分比R2adj为99.37%，表明剔除非显著项后优化得到的模型显著，可信度高。

表5 表面粗糙度模型的方差分析Tab.5 ANOVA for surface roughness model

图6 残差正态概率分布图Fig.6 Normal probability plot for the residual

图6 为通过Minitab拟合得到的残差概率分布图，其中图6a所示图形两侧尾部较短，左边的散点朝直线上方弯曲呈短尾分布，右边朝直线下方弯曲，材料去除率RMR的残差相对于标准正态分布更集中靠近均值；图6b所示图形两侧尾部较长，图形左边散点朝直线上方弯曲，右边朝直线下方弯曲呈长尾分布，表明表面粗糙度Ra的残差较正态分布偏离的数据相对更多。由图6a和图6b可以看出，绝大部分残差的散点都落在预测值线的周围，偏离直线的程度小，因此可认为残差服从正态分布，模型的拟合良好。

3 基于响应曲面图的工艺参数优化

试验中有4个自变量，2个优化目标，任意选取其中一显著交互项，以2个工艺参数为x轴、y轴，响应值为z轴，其余2个工艺参数保持0水平，建立响应曲面，见图7和图8。图7为磨粒粒径D和磨粒浓度C对材料去除率RMR的响应曲面图，可以看出，随着磨粒粒径D的增大，相同条件下能够被带入刀片与抛光垫之间的磨粒数量逐渐减少，从而导致RMR减小；而随着磨粒粒径D的减小，相同条件下磨粒浓度C的增大直接导致参与机械磨削的磨粒数量增加，从而使得RMR增大。图8为抛光压力p与磨粒粒径D对表面粗糙度Ra的响应曲面图，可以看出，适当减小抛光压力能获得较好的表面质量，当抛光压力p超过临界值时，磨粒压入刀片表面的深度逐渐增大，导致磨粒在表面机械作用的磨痕逐渐加深，反而在一定程度上导致表面的质量降低。由图7和图8可以看出，在设计自变量空间中存在最优解。

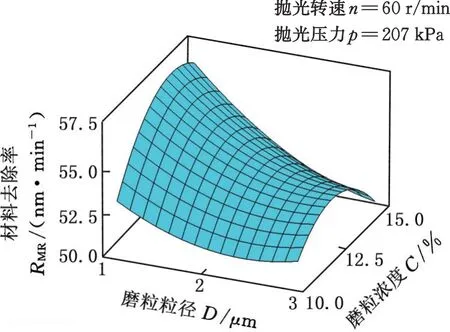
图7 材料去除率相对于D、C响应曲面图Fig.7 Influence of abrasive particle size and abrasive concentration on MRR

图8 表面粗糙度相对于p、D响应曲面图Fig.8 Influence of polishing pressure and abrasive particle size on surface roughness

RSM在分析多变量反应曲面最佳化的过程中，采用渴望函数来整合各个响应值，通过各个自变量的渴望函数计算获得各自的渴望函数值，再将加权几何平均作为优化的综合指标。

根据得出的材料去除率RMR和表面粗糙度Ra与工艺参数的二阶响应曲面方程，利用Minitab的响应优化器对工艺参数进行优化，使YG8硬质合金刀片CMP过程在获得高表面精度的同时保持更大的RMR，根据自变量的实际范围设定Ra最小化和RMR最大化为优化目标,并给定Ra的上限值和RMR的下限值，优化后的结果见图9。当n=65.5 r/min，p=156.7 kPa，D=1.1 μm，C=14%时，得到最小表面粗糙度预测值Ra=0.019 μm，材料去除率RMR=56.6 nm/min，Ra的满意度SRa为1，RMR的满意度SRMR为0.751 31，整体满意度S为0.866 8。

图9 响应曲面法优化获得的最佳工艺参数Fig.9 Optimum combination of process parameters obtained by using response surface methodology

4 试验验证

为进一步验证预测模型的正确性，在由式（2）和式（3）表示的材料去除率RMR和表面粗糙度Ra预测模型的适用参数范围内随机选取工艺参数进行试验，试验时抛光垫、抛光液等加工条件与CCD试验时的加工条件相同，工艺参数和试验结果见表6，其中第3组的工艺参数为优化后的试验参数。

利用表6在不同工艺参数组合下加工得到的材料去除率RMR和表面粗糙度Ra的实测值与式（2）和式（3）计算得到的RMR和Ra预测值进行对比，见图10和图11。由图10和图11可以看出，RMR和Ra的实测值RMR,m和Ram分别与预测值RMR,p和Rap的结果基本吻合，且误差均在10%以内。

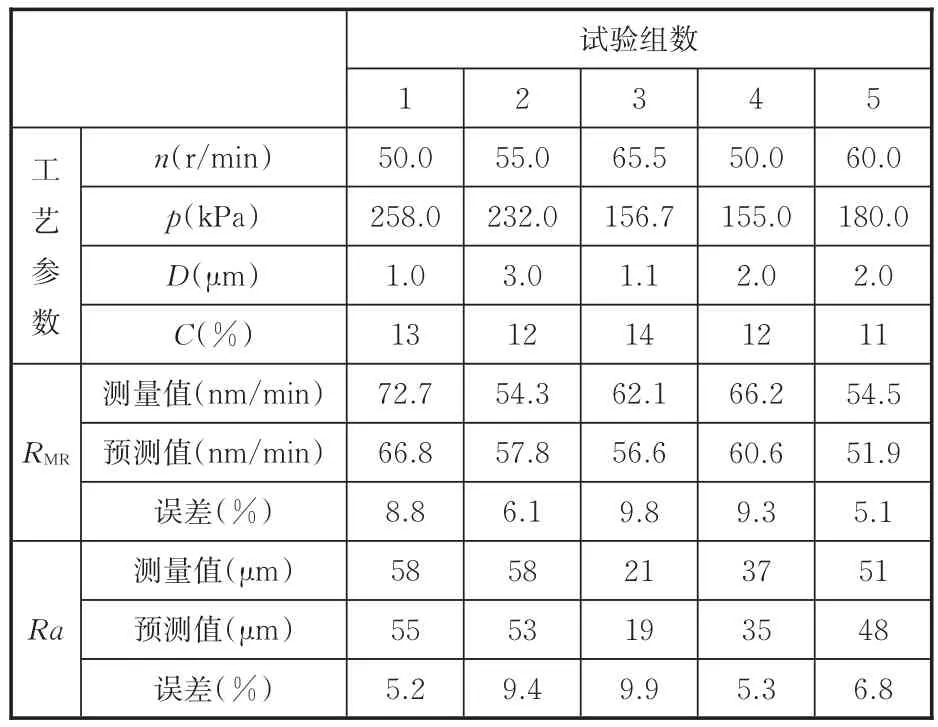
表6 验证试验的工艺参数与结果Tab.6 Process parameters and results for verification test

图10 材料去除率预测值和实测值比较Fig.10 Comparison between the predicted and measured values of MRR

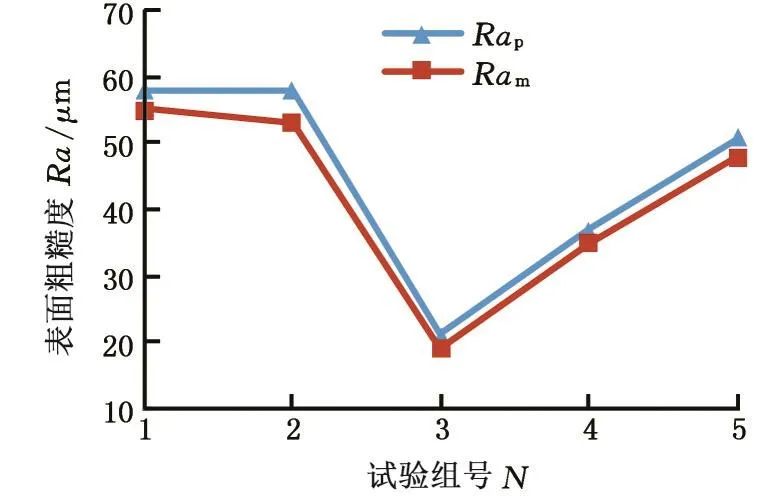
图11 表面粗糙度预测值和实测值比较Fig.11 Comparison between the predicted and measured values of surface roughness

利用VHX-5000超景深三维显微镜系统（日本基恩士）观察CMP加工前和试验1～试验5 CMP加工后YG8硬质合金刀片前刀面刀尖的表面形貌，如图12所示。由图12可以看出，CMP加工前刀片表面存在大量磨痕、凹坑和裂纹的缺陷；CMP加工后，试验1和试验4的刀片表面均存在磨粒过抛的现象，且留有磨粒划伤的划痕；试验2和试验5的刀片表面残余一部分的凹坑没有完全去除；试验3的刀片表面光滑平坦，几乎没有表面缺陷。

图12 CMP加工后的刀片表面形貌Fig.12 Surface morphology of blade after CMP

通过试验验证分析可知：用随机组合的工艺参数进行试验，表面粗糙度和材料去除率的实测值与预测值的误差均在10%以内，证明了预测模型的准确性；使用优化后的最佳工艺参数组合抛光硬质合金刀片得到的刀片表面光滑平坦，其表面质量明显优于随机组合的工艺参数抛光刀片得到表面质量。

5 结论

（1）通过采用CCD试验方案，显著性分析结果表明，在本试验环境中4个工艺参数对材料去除率RMR的影响程度从高到底依次为：抛光转速n、磨粒粒径D、抛光压力p、磨粒浓度C；对表面粗糙度Ra的影响程度从高到低为：磨粒浓度C、抛光压力p、抛光转速n、磨粒粒径D。

（2）基于RSM对RMR和Ra的试验结果与工艺参数进行方差分析，以减小表面粗糙度、增大材料去除率为目标，分别建立了关于RMR和Ra与工艺参数之间的多元二阶回归预测模型，并对模型进行理论验证，结果表明模型的可靠性高，拟合效果好。

（3）通过响应曲面优化获得的最佳工艺参数为抛光转速65.5 r/min、抛光压力156.7 kPa、磨粒粒径1.1 μm、磨粒浓度（质量分数）14%，此时得到最小表面粗糙度预测值Ra=0.019 μm，材料去除率RMR=56.6 nm/min。对YG8硬质合金刀片CMP过程中模型预测的准确性进行验证，并比较5组CMP加工试验的实测值和预测值，计算得到RMR和Ra实测值与预测值的平均相对误差均小于10%，从而验证了预测模型的准确性。