砂轮表面形貌定量评价及修整效果研究

刘 伟 商圆圆 邓朝晖 刘仁通

1.湖南科技大学智能制造研究院难加工材料高效精密加工湖南省重点实验室，湘潭，411201

2.湖南科技大学机电工程学院，湘潭，411201

0 引言

砂轮表面形貌特征作为磨削过程的重要影响因素，对砂轮的磨削性能有着决定性作用。砂轮表面磨粒在磨削过程中因磨损会产生钝化、破碎和脱落，因此需要对砂轮表面进行修整来保证砂轮表面磨粒的磨削性能。另外，修整后砂轮表面形貌特征也是评价修整好坏的重要参考因素。

近年来，国内外专家学者对砂轮表面形貌评价进行了一系列研究。谢晋等［1］建立了有效磨粒出刃高度、磨粒出刃角和磨粒出刃同形度的特征参数模式，对修整后磨粒微观出刃形貌进行了评价。韦凤［2］通过非接触检测技术和图像处理技术建立了砂轮表面微观形貌的参数化表征模式，通过有效磨粒出露体积和有效磨粒出露数来评价砂轮表面形貌。王帅［3］采用LK-G80激光测距仪对砂轮轮廓圆度进行测量，用砂轮磨粒等高性来评价砂轮的形貌特征。党希敏等［4］采用分形维数和等价出刃尺寸来分别评价砂轮磨粒的破碎程度和砂轮磨粒出刃的均匀程度。邓朝晖等［5］用积分光密度值对砂轮表面磨粒磨刃二面角进行评价。柯晓龙等［6］采用圆跳动误差值与圆弧半径误差值来评价修整后圆弧砂轮的表面形貌。以上学者从磨粒微观出刃角度对砂轮表面形貌进行了评价，但是相关评价方法并不全面，没有评定砂轮表面磨粒的分布情况。

苏玲玲等［7］采用静态磨刃密度CS、磨粒分布均匀性CV两个评价指标定量评价了磨粒在磨具表面的分布形态。石际亮［8］针对单层CBN砂轮磨粒的分布问题，提出将磨粒方差和磨粒堆积连通域的比面积方差相结合的综合评价方法。这两种方法仅评价了砂轮表面磨粒的分布情况，并未评价磨粒的出刃情况。

霍凤伟等［9］对砂轮表面进行测量和分析，重构出砂轮表面三维形貌，计算出砂轮的磨粒出刃高度、有效磨粒数和磨粒间距等参数，并用此参数来评价砂轮。李厦等［10］检测砂轮的三维表面形貌，对磨粒密度、出露高度、有效出露高度等特征参数进行了研究。张涛［11］将ISO25178-2标准中提到的幅值参数和空间参数应用于砂轮表面形貌的评价。康伟［12］采用幅值参数、空间参数、综合参数、功能体积参数来综合评价砂轮表面形貌特征。TAMAKI等［13］用磨粒最大出露高度、切削点径向分布和磨粒平均出露高度来评价金属结合剂金刚石砂轮的形貌特征。以上评价方法对砂轮表面磨粒的出刃和分布情况进行了综合评定，评价指标主要针对磨粒分布、磨粒出刃高度、磨粒微观出刃情况、切削刃数等。但现有的评价方法，或检测工作量大，或检测精度不高，或检测效率较低，不适合推广。

砂轮表面磨粒出刃面积检测比较简单，检测效率高，可作为评价砂轮表面形貌的重要特征参数之一，但目前有关砂轮表面磨粒出刃面积的研究鲜见报道。本文基于砂轮表面磨粒出刃面积，提出砂轮表面磨粒出刃面积率的概念，在此基础上提出磨粒出刃度和磨粒出刃面积分散度两个指标来评价砂轮表面形貌特征。采用80号的绿色碳化硅砂轮作为修整器滚轮对100号的树脂结合剂金刚石砂轮进行修整实验，研究在不同修整条件下金刚石砂轮的磨粒出刃度和磨粒出刃面积分散度，以及不同砂轮表面形貌特征下砂轮的磨削性能。

1 两个砂轮表面形貌评价指标的提出

1.1 理论磨粒出刃面积率

金刚石砂轮表面的磨粒与结合剂平面相交的截面面积总和与砂轮表面面积之比为磨粒出刃面积率，即单位面积中磨粒的出刃面积的百分比。通过砂轮粒度号和砂轮浓度可以求出理论砂轮磨粒出刃面积率Sr，计算流程如图1所示，其中，砂轮粒度号对应磨粒直径，砂轮浓度对应磨粒的体积分数。已知磨粒出刃面积Sg与磨粒直径dg、出刃高度hg这两个随机量相关，因此需要求解二者的联合概率密度f(dg,hg)，从而得到等效出刃面积Sg-e，最后结合磨粒面积密度 ρgnS［14］求出 Sr。

图1 计算流程图Fig.1 Calculation flow chart

1.1.1 磨粒出刃面积

假设磨粒为球形，图2所示为磨粒出刃面积几何关系，可以得到磨粒出刃半径rg和磨粒出刃面积Sg如下：

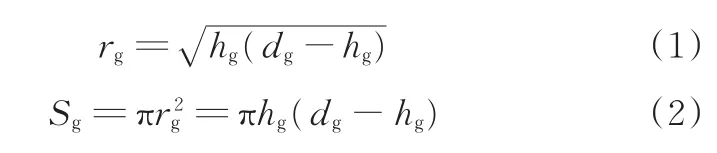
如图2所示，结合剂平面越低，磨粒出刃高度越高，磨粒出刃面积越大。磨粒出刃面积大致反映了磨粒出刃高度的情况。

1.1.2 联合概率密度

文献［15］通过分析测量大量磨粒，得出dg符合正态分布的结论。正态分布的概率密度函数f(x)如下：

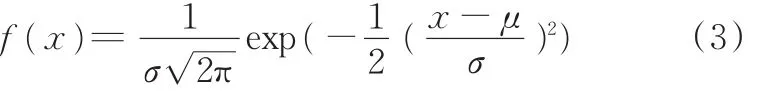
式中，x为自变量；μ为正态分布均值；σ为正态分布方差。

根据正态分布的“3σ准则”选取σ的值，有

图2 磨粒出刃面积几何关系图Fig.2 Geometric relation diagram of grain protrusion area

式中，xmax、xmin分别为自变量x的最大值与最小值。可得dg的概率密度函数f(dg)如下：

式中，dgmax、dgmin分别为砂轮表面磨粒最大直径与最小直径，可根据砂轮粒度号查表得到。

hg一般也服从正态分布［9］，当金刚石磨粒的出刃高度超过其粒径的1/3时，在高速旋转切削过程中容易破碎脱落［14］，因此取砂轮表面磨粒最大出刃高度hgmax为μ1/3，最小出刃高度hgmin为0，即磨粒出刃高度在0～μ1/3之间服从正态分布，可得hg的概率密度函数

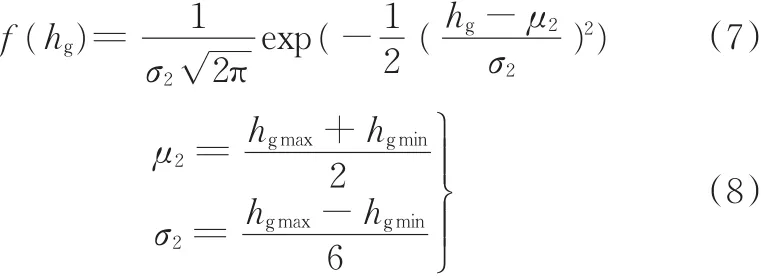
dg和hg都服从正态分布，其联合概率密度函数

其中ρ为联合分布的相关系数，计算公式如下［16］：

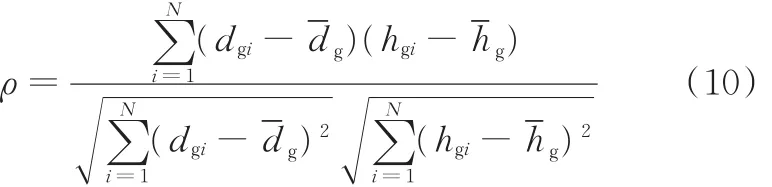
式中，-dg、-hg分别为磨粒直径、磨粒出刃高度的平均值，即μ1、μ2；i为磨粒颗数。

1.1.3 等效出刃面积

为了描述磨粒的平均出刃面积，考虑到磨粒直径和磨粒出刃高度的分布，以及其联合概率密度函数，定义磨粒等效出刃面积Sg-e如下（假设磨粒为球形）：

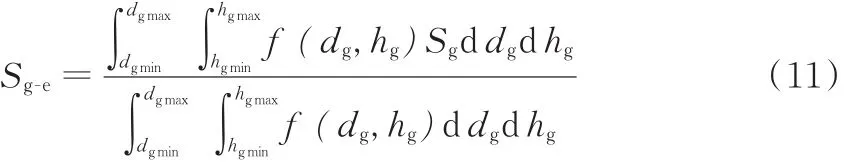
1.1.4 磨粒面积密度

文献［14］提出了磨粒面积密度ρgnS的概念，即单位面积砂轮表面的磨粒数，它与砂轮表面磨粒平均间距Lg直接相关：

式中，Vg-e为砂轮表面磨粒的等效体积；φ为砂轮中磨粒的体积分数。

对于球形磨粒，其等效体积

1.1.5 理论磨粒出刃面积率

为了更好、更方便地评价砂轮表面磨粒的出刃程度，提出砂轮表面磨粒出刃面积率Sr的概念，即单位面积中磨粒的出刃面积百分比，其表达式为

对于100号的浓度为100的金刚石砂轮，其体积分数为25%［14］，则面积分数也为25%，通过式（14）计算可得到理论磨粒出刃面积率为26.075%，两者误差小于5%，证明在等效出刃面积计算中将磨粒形状假设为球形，并用于计算理论磨粒出刃面积率，是合理有效的。

1.2 磨粒出刃度

实际磨粒出刃面积率的具体计算过程如图3所示。采用超景深三维显微系统VHX-500FE对粒度100号（磨粒直径在150～160 μm之间）、浓度100的树脂结合剂金刚石砂轮表面形貌进行图像采集，采集图像如图4所示。

图3 实际磨粒出刃面积率计算流程Fig.3 Flow chart of calculating method of actual grain protrusion area rate

图4 砂轮表面形貌采集图Fig.4 Collected image of grinding wheel surface topography

用MATLAB编程对砂轮表面形貌进行灰度化（用加权平均值法将彩色图转化为灰度图）、亮度均衡化（用直方图均衡化使图像的灰度均匀分布，从而使图像细节清晰）、阈值处理（保留图片高亮部分）、滤波（采用中值滤波，滤除一些不必要的黑色小块）、图像融合（去除图像中的白色小块，使黑色小块完整）等一系列图像处理过程，处理后得到如图5所示的图像，并通过MATLAB编程读取每个完整黑色小块的像素，计算出黑色小块像素之和占图像总像素的比例，即为实际磨粒出刃面积率。多次采集砂轮表面形貌图，计算其磨粒出刃面积率，并取平均值即可得到砂轮表面实际磨粒出刃面积率。

图5 砂轮表面形貌图像处理图Fig.5 Processed image of grinding wheel surface topography

磨粒出刃度准确描述了砂轮表面磨粒的出刃程度：当βd≤1时，磨粒出刃度越高，则砂轮修整越充分；但当βd＞1时，砂轮过修，其磨削性能会变差。

1.3 磨粒出刃面积分散度

经过多次采集不同修整条件下金刚石砂轮表面磨粒出刃面积，并绘制磨粒出刃面积频数分布见图6，其图形均呈单峰分布，峰值向左偏倚，右边柱状高度逐渐变小直到趋近于横坐标轴。磨粒出刃面积的大小分布集中，则磨粒出刃面积频数分布图的单峰为瘦高型；反之，为矮胖型。

图6 磨粒出刃面积频数分布直方图Fig.6 Frequency distribution histogram of grain protrusion area

为了描述砂轮表面磨粒出刃面积的等值性，定义磨粒出刃面积分散度δs。δs为频数分布直方图中柱形高度超过 fve（约 0.606 fv）［1］的磨粒出刃面积的分布范围大小，即分布范围的极差值。fv为频数分布直方图的峰值，如图6所示。δs越小，磨粒出刃面积Sg的分布越集中，磨粒出刃面积的等值性越好，则磨粒出刃高度的等高性就越好，磨削过程中参与磨削的磨粒数就越多；当δs为零时，磨粒出刃面积具有理想的等值性。

2 修整对砂轮表面形貌的影响

2.1 实验条件

修整实验在高精密数控卧轴矩形台平面磨床MGK7120×6/F上进行，砂轮为粒度100号、浓度100、外径200 mm的树脂结合剂金刚石砂轮，采用电动金刚石砂轮修整器GIN-DTM100，修整器滚轮选用80号绿色碳化硅砂轮，滚轮直径为63 mm。修整实验装置如图7所示，修整器机座吸附在磨床工作台上，修整器滚轮主轴轴线与磨床主轴轴线平行并在同一铅垂面内。修整器滚轮转向与金刚石砂轮转向相反，修整器滚轮转速为108 r/min。

图7 修整实验装置图Fig.7 Grinding wheel dressing experiment device

2.2 修整深度对βd和δs的影响

修整采用两种方式，方式一是1次进给，修整深度为df，方式二是修整深度分5次进给，累计深度为df。两种修整得到的βd和δs如图8所示。由图8可知，方式一的βd比方式二的βd小，方式一的δs比方式二的δs大。由于方式二的单次修整深度比方式一的单次修整深度小，磨削阻力较小，使得修整后砂轮表面磨粒破碎和脱落要少，βd较大，δs较小。在修整深度小的情况下，磨削阻力小，对砂轮表面的破坏作用较小，两种修整方式差别不大；在修整深度较大时，则需要采用方式二来改善砂轮表面形貌。

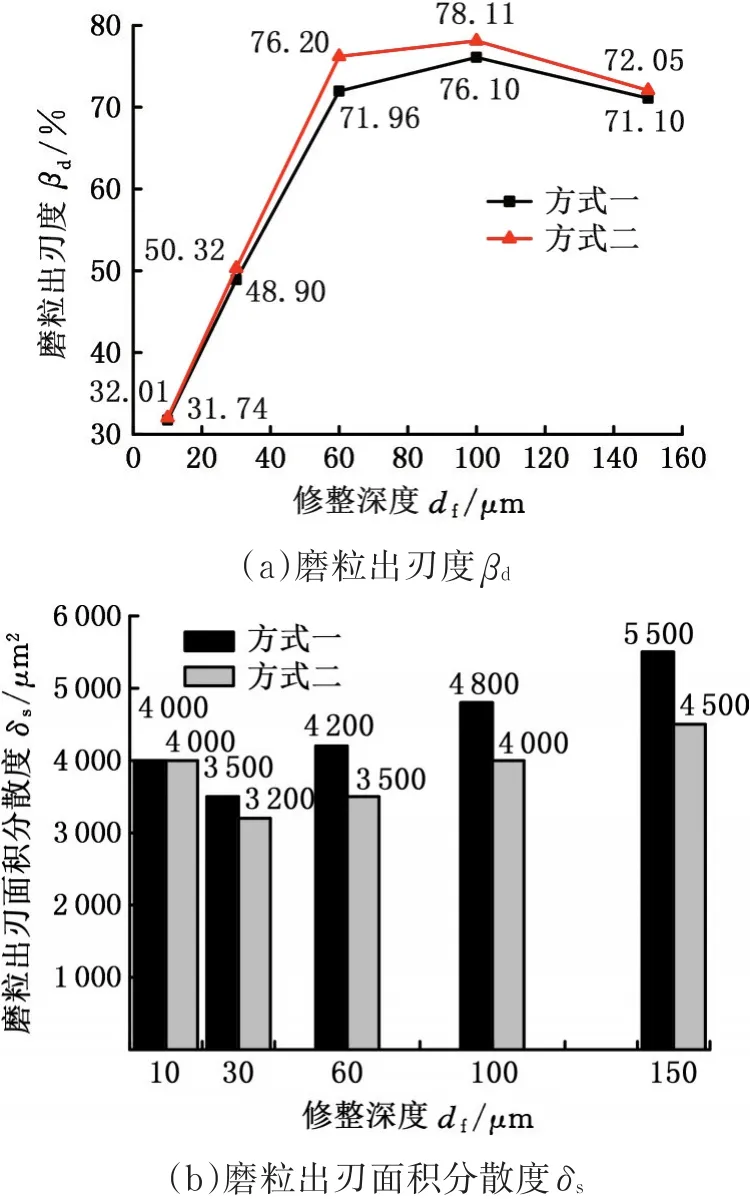
图8 修整深度对βd和δs的影响Fig.8 Influence of dressing depth on the βdand δs

修整深度对砂轮表面磨粒出刃度的影响如图8a所示，随着修整深度的增大，βd递增，当修整深度达到100 μm时，βd开始减小。修整前，磨粒镶嵌在结合剂中，磨粒出刃高度较小，出刃面积较小；用滚轮进行修整时，去除部分结合剂，使磨粒从结合剂中显露出来，磨粒出刃面积逐渐增大，βd增大。但修整深度过大，超过100 μm时，即超过磨粒直径的2/3时，会使部分出刃高度大的磨粒直接脱落产生凹坑；同时，磨削阻力变大，造成磨粒不规则破碎，使得磨粒出刃面积率减小，βd减小。

修整深度对磨粒出刃面积分散度的影响如图8b所示，随着修整深度增大，δs先减小后增大。当修整深度由10 μm增大到30 μm时，δs减小；此时，砂轮表面结合剂经修整去除，磨粒从结合剂中显露出来，δs减小，磨粒出刃面积的等值性增强。当修整深度由30 μm增大到150 μm时，δs增大，磨粒出刃面积的等值性减弱；由于修整深度增大，磨削阻力过大，会使部分出刃高度大的磨粒脱落产生凹坑，也会造成磨粒破碎，使δs增大，等值性减弱，砂轮表面磨粒的出刃等高性降低。

从以上结果可以看出，修整深度增大，砂轮表面磨粒出刃度增大，砂轮表面磨粒的平均出刃高度增大，参与磨削的磨粒数增多；但修整深度过大，磨粒出刃面积的等值性减弱，磨粒出刃高度的等高性减弱，因此为了保证砂轮良好的磨粒出刃度和磨粒出刃面积的等值性，建议采用较小的修整深度，多次进给修整砂轮。

2.3 修整速比对βd和δs的影响

砂轮修整速比为修整滚轮线速度与金刚石砂轮线速度的比值［17-18］。修整滚轮线速度经转速换算为0.356 m/s，砂轮线速度分别取1.78 m/s、0.89 m/s、0.59 m/s、0.5 m/s、0.45 m/s，则其速比为0.2、0.4、0.6、0.7、0.8。图9为修整深度为30 μm时βd和δs的变化关系图，随着砂轮修整速比增大，βd减小，δs增大，即砂轮表面磨粒平均出刃高度减小，砂轮出刃面积等值性降低，砂轮出刃高度的等高性减弱，砂轮磨削性能降低。由于砂轮速比增大，砂轮线速度减小，则砂轮和修整滚轮的相对速度减小，切削作用因为相对速度减小而变小，挤压作用随之增强，砂轮表面磨粒出刃情况变差，出现破碎和钝化，因此βd减小，δs增大。在修整砂轮时，为了提高修整效果，改善砂轮磨削性能，建议采用修整速比小的修整方案。

图9 修整速比对砂轮表面特征参数的影响Fig.9 Effect of dressing ratio on characteristic parameters of grinding wheel surface

3 不同表面形貌砂轮的磨削性能

3.1 实验条件

磨削实验在高精密数控卧轴矩形台平面磨床MGK7120×6/F上进行，工件为氧化锆陶瓷，尺寸为20 mm×20 mm×10 mm。为研究修整后不同表面形貌砂轮的磨削性能，采用瑞士Kistler生产的磨削力测量仪检测磨削切向力、法向力，采用德国Mahr Gmbh生产的便携型表面结构测量仪MarSurf M300检测工件表面粗糙度。磨削实验中，砂轮转速为1200 r/min，工件速度为40 mm/s，磨削深度为10 μm。磨削实验装置如图10所示。

图10 磨削实验装置图Fig.10 Grinding test device

3.2 结果分析

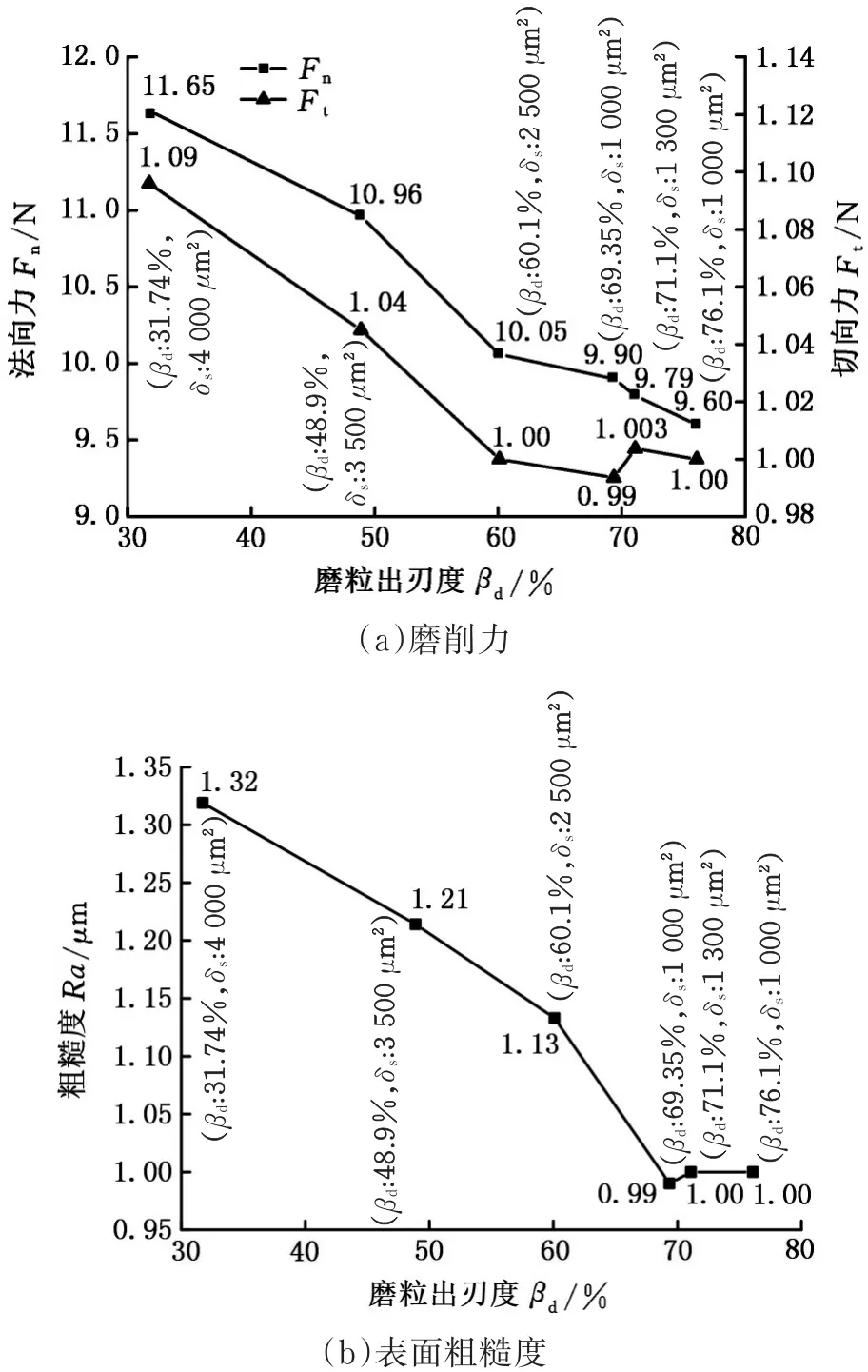
图11 磨削力及表面粗糙度与砂轮表面特征参数的关系图Fig.11 Relationship between grinding force and surface roughness and characteristic parameters of grinding wheel surface

不同的砂轮磨粒出刃度以及磨粒出刃面积分散度的砂轮磨削氧化锆陶瓷的法向力、切向力、工件表面粗糙度如图11所示，随着βd增大，δs减小，砂轮磨削的法向力和切向力减小。法向力、切向力在βd为60.1%、δs为 2 500 μm2后减小较为平缓；在βd为 69.35%、δs为 1 000 μm2后，切向力减小到0.993 6 N后略微上升，表面粗糙度减小到0.99 μm后有上升趋势。砂轮修整后随着βd增大，δs减小，砂轮表面磨粒平均出刃面积增大，参与磨削的磨粒数增多，容屑空间增大，砂轮的磨削性能增强，因此法向磨削力和切向磨削力下降，磨削表面质量变好，工件表面粗糙度减小。当砂轮继续修整，βd增量和δs下降速度会变缓，甚至逆向变化，此时修整滚轮对磨粒会造成一定程度的磨损，导致砂轮磨削性能减弱，即磨削力有略微增大，表面粗糙度增大。

根据实验对100号树脂结合剂金刚石砂轮进行修整，对不同磨粒出刃度、磨粒出刃面积分散度下磨削力、表面粗糙度的变化趋势分析可知：当修整深度为30 μm、修整速比为0.2时，βd为69.35%、δs为1 000 μm2时，修整质量最好，砂轮磨削性能最佳。

4 结论

（1）通过建立理论磨粒面积率Sr的计算公式，定义了磨粒出刃度βd和磨粒出刃面积分散度δs两个砂轮表面形貌评价指标。βd反映了砂轮磨粒出刃程度；δs反映了磨粒出刃面积的等值性。

（2）用βd和δs评价不同修整条件对砂轮表面形貌的影响，得到了采用较小的修整深度，多次进给修整砂轮，以及较小的修整速比时，βd较大，δs较小，修整效果更好。

（3）把修整得到的不同βd和δs的砂轮进行磨削实验，发现当修整深度为30 μm、修整速比为0.2时，βd为 69.35%、δs为 1 000 μm2，修整质量最好，砂轮磨削性能最佳。

（4）所提出的βd、δs两个指标能对修整后的砂轮表面形貌进行准确评价，且评价方法简单，检测效率和精度较高，检测结果直观，是砂轮表面形貌有效的评价方法，可进一步指导砂轮精密磨削，对砂轮形貌建模及其有限元仿真具有指导作用。