基于多层复杂网络与共演化策略的合作演化的研究

卿伦科

（杭州电子科技大学计算机学院，杭州310018）

0 引言

从图论发展而来的复杂网络科学，一直都被各科学学科作为理论范本，用于建立贴近现实现象的模型。复杂网络的研究工作主要分为两类，一类是对网络上主体之间交互的动力学研究，另一类是对网络自身拓扑结构的动力学研究。长期以来，演化博弈论用于研究网络上主体之间交互的动力学，根据网络的结构和博弈规则以及一些改进的策略来研究主体策略的演化过程。现实网络的结构不断发生变化，网络结构的变化与个体在网络中演化过程存在着不可忽视的必然联系。网络的共演化策略，结合了网络的两种动力学研究工作，用于动态网络中合作演化的研究。然而，现有的工作大多针对某一特定的网络进行单层网络建模，如在社交网站上分析舆论导向或人物关系，在物理交通网上分析流量和交通部署方案，等等。从经济、文化到政治，各种相互关联的网络交织在我们每时每刻的生活之中。这些网络之间看似没有直接的交互连接，但网络间的相互影响是潜移默化甚至难以被明显察觉的。一些非常有价值的研究表明，我们生活在一个充分连接的世界，一些看起来毫不起眼的变化，可能在另一个领域或网络中引起巨大的变故甚至灾难，或者说是出乎人意料的结局。近几年，国际上提出了“多层复杂网络”以及“网络中的网络”等新兴概念模型，成为了复杂网络领域最前沿的研究方向之一。

针对当前研究的建模过于简化的问题，本文提出了一种基于多层网络的网络共演化策略。由于个体同时身处多个网络之中，在个体掌握有限的资源（如时间、精力、财富等）的前提下，完全理性个体通常需要对资源进行有效地部署来实现利益最大化。因此该策略使得个体自适应断边，回收资源后，在其他某层中随机连边，重新部署资源。通过本策略的C++仿真实验，证明了该策略能有效促进合作的演化。

1 模型

本节中的多层网络是由m层相互依赖的单层复杂网络（ER随机网络或BA无标度网络）排列组合，每层网络的规模大小N相同，网络拓扑结构不同。个体在各层网络中同时进行同步囚徒困境博弈。每个节点为一个博弈对象，节点在各层网络中与其当层网络中的邻居节点进行博弈。对于一个个体i，用Gk ij=1表示在第k层网络中交互个体i和交互个体j相连（互为邻居），反之则值为0。用Sk i(t)=1表示随时间演化的第t轮中个体i在第k层采取合作策略，值为0则是采取背叛策略，网络的初始化时，主体有50%的几率为合作者。与合作者的博弈时，合作者的收益为R=1，背叛者的收益为T=bT=1.5；与背叛者的博弈中，合作者的收益为S=-1，背叛者的收益为P=0，这一博弈矩阵是严格的囚徒困境博弈，满足 T＞R＞P＞S 且 2R＞T+S。根据此规则个体i在某一层中与其所有邻居博弈后得到一个收益值pk i(t)，表示在第t代中个体i在第k层博弈后的收益，个体i在第k轮网络博弈后得到的总收益定义为：

在多层网络中，合作者比例cˉ的计算方法为：

每一轮的囚徒困境博弈结束后，对每个个体进行同步的策略更新，和单层网络中的更新步骤不同的是，对于进行策略更新的主体i，随机选取其所在的一层网络l，随机选取该网络中的一位邻居j，主体i在本层中学习其邻居j的概率用比例学习方程进行计算：

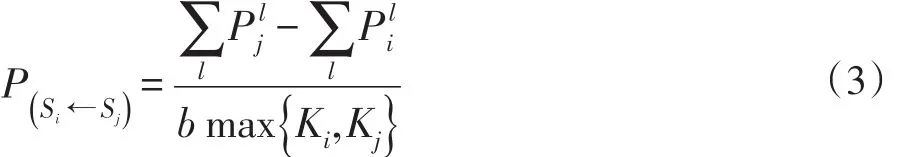
2 共演化规则

在个体掌握有限的资源（如时间、精力、财富等）的前提下，完全理性个体可通过对资源进行有效部署来实现利益最大化。在种群初始化时，个体在网络中的度的总和被视为其可支配的资源。每个网络中的度的大小kl视为其分配在该网络上的资源的量。设主体的分离系数为T∈(0 ,1]，值越大表示个体越难以容忍投资收益比较低的网络，其更倾向于回收在网络中的资源。通常地，假设复杂网络中的主体能够获取邻居当前的收益以及其周围的环境（即邻居的邻居）。在进行一轮的PDG后，主体会根据自己的收益和投入的资源，找到投资收益比V最小的层，若该值小于的分离系数，则准备回收一个单元的资源，即断开一条连接。此时主体会首先遍历其所有邻居找到友好度F最低的个体，两个值的计算方法如下：

约束条件（6）表示客体的博弈环境很不友好，正在吞噬自己的利益并令人难以忍受；约束条件（7）是防止出现孤立节点，保证图的连通性。若资源回收成功，即成功断开连接，则将回收的资源重新分配给其他层，即建立新连接。个体找到投资收益比最高的层，如果找到了多层，就在这之间随机选取一层，然后在该层中随机选取节点，若选中的节点是已有连接的邻居节点则重新选择节点建立连接。

3 实验结果分析

本策略在多层网络中的合作演化过程如图1所示，纵坐标为种群合作者个体比例，横坐标为演化代数，红、蓝曲线分别为四层ER、BA网络中的演化过程。为了验证策略的有效性，还进行了一组标准对照仿真实验，让初始种群在无网络共演化的静态的多层网络下进行合作演化，如绿色实线所示。较为明显地，在无策略的多层网络下，种群的合作个体在前10代迅速从50%下降到20%，进而在一百代左右时，合作者被背叛者全部侵略，主导整个种群。相反地，在采取本节策略的ER多层网络（红色实线）和BA多层网络（蓝色实线）中合作个体比例在前60代左右有持续下降至40%，但随着个体的自适应调整，个体将更多的边分配到收益较好的网络之中，在任一网络中，通过自适应调整，合作者抱团，进而逐渐主导种群，大约在200代时合作者比例收敛与65%上下。合作行为不仅得到了保护，还有积极演化趋势直至最后收敛。我们也同样验证了BA网络-无策略的演化过程，其演化过程与绿线呈相同趋势，且拟合度较高。由于我们只是为了体现该策略的有效性，为去除重要参数分离系数的影响，我们将分离系数设置为1，即种群中的主体希望自己的每一次投资都得到正收益，保证局部最优解。为了进一步理解这一现象，以及两种不同的网络拓扑结构对合作产生的影响，我们需要深入分析各参数与演化过程的关系。

图1 共演化策略对合作演化的影响

在保证参数和随机种子相同的情况下，进行图1的重复试验，观察网络的不同时期的拓扑结构的动力变化，如图2所示。由于该实验在200代时已经趋于收敛状态，我们取了1、50、200这三个时间节点进行描绘。红色、蓝色柱状图分别为ER网络、BA网络中的度分布图，由于背叛者侵蚀合作者的利益，其友好值F较低，易被断边，而合作者之间相对更易抱团，最后形成“背叛者孤岛”。因此，随着时间推移，即使随机网络在初始时，平均度为4×4，服从泊松分布，涌现出大节点，和无标度特性，其度分布会向着幂律分布的结构演化，逐渐呈现出“长尾状”。在接近收敛时，两个网络的度分布也十分相似。这与大多数的现实网络最终趋于幂律分布这一现实规律相符。

在验证了本节策略有利合作演化后，接下来我们研究了实验的重要参数——分离系数T对合作演化的影响，分离系数T越大意味着主体对投资回报的期待更高，所以更难容忍被低回报投资，在低回报的网络中更倾向于回收资源。为了排除网络结构的随机性影响数据样本，本实验控制程序的随机种子保证了网络的初始状态以及主体的初始状态都是一样的。对于网络结构更复杂的BA网络而言（如图3a），不同T的演化趋势却较为相似，这意味着网络的结构演化过程相近。而对于网络结构相对简单的ER网络而言，其在不同T的影响下，演化趋势拟合度更低，意味着在没有超大节点的去中心化的环境中结构演化过程更加随机。

总体地，从两图的演化规律来看，随着T的减小，种群的演化需要更多时间才能收敛。另外，T取最大值时，收敛后合作者比例却不是最大的，也就是说，在可行的范围内，对低回报网络的适当容忍或观望反而可以促进种群的合作，使得主体得到更多的利益。值得注意的是，BA网络当T降至0.3时合作演化失败，而在ER网络中这一标准是0.2。关系复杂的网络合作演化的门槛更高，各主体需要有较强的投资回报期待才能抵消部分hub节点的消极影响。在随机网络中，各主体的资源初始时相对均匀，因此促使合作演化的门槛较低。

为了进一步验证共演化策略的有效性，本文对不同种群大小的多层网络进行了对照研究。如图4所示，描绘了基于该策略下不同种群大小的两种多层上的合作演化图。其中每个网络的层数为m=4，平均度d=4，分离系数T=0.6。经过试验分析，总体来看，种群的大小不影响合作的大致演化趋势。然而，基于BA无标度网络的多层网络中，其结构更为复杂，存在少量对网络影响大的节点，随着种群规模的变大，由于长尾效应，将有更多的度较小的个体加入到网络中，这些个体手容易受大节点影响，因此收敛时的回归值会有轻微的上升；而基于ER随机网络的多层网络中，网络的结构均匀并附有随机性，其演化收敛时的结果更多取决于网络生成时的初始态及主体的动力过程，因此不受制于种群大小的变化。

图2 P（D）-Generation度分布随时间的演化

图3 分离系数对合作演化的影响。N=400，d=4，m=4

最后本文研究了多层结构的层变量对演化过程的影响，如图5所示。实验结果表明在两层网络结构中，层间相互约束的作用相对其他多层网络较少，没有明显优于单层网络。随着网络层数的增加，网络结构变得更为复杂，合作者抱团难度也随之增加，收敛的时间成本增加，在二十层时，合作者难以快速抱团，最终合作行为消失。在这之间的范围内，层数的变化亦不影响合作演化的最终的收敛结果。

4 结语

本文提出了基于多层网络的网络共演化策略，用相互依赖的多层复杂网络模拟真实环境中的由多层网络同步进行演化，相互影响的特征；用自适应断边随机连边的多层网络共演化方法模拟真实网络中，网络结构不断发生变化的特点。通过仿真实验验证了该策略的有效性，有助于更深刻地理解合作的涌现。

图4 种群大小N对合作演化的影响。m=4，d=4，T=0.6

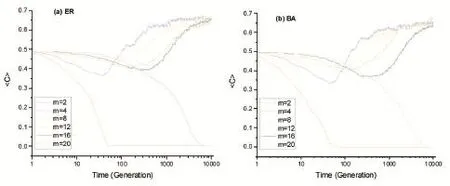
图5 网络层数对合作演化的影响。N=200，d=4，T=0.6