基于改进相似度的协同过滤算法
高兴前,王晓峰
(上海海事大学信息工程学院,上海201306)
0 引言
随着互联网和信息技术的迅速发展,网络中所蕴含的信息量呈指数级增长,导致了信息过载等一系列问题。据国际数据公司IDC(International Data Corpora⁃tion)2012年报告显示:预计到2020年,全球数据总量将达到35.2ZB,这一数据量是2011年的22倍[1],而在这海量数据中用户很难发现自己感兴趣的部分。推荐系统因此应运而生,通过分析用户的历史数据建模,然后将用户感兴趣信息推荐给用户。
协同过滤CF(Collaborative Filtering)无疑是当前使用最为广泛的推荐算法之一[2],最早在1992年由Goldberg等人提出[3]。它依据用户-项目评分数据,计算用户(或项目)之间的相似度,然后将一个用户感兴趣的项目推荐给其他与之相似的用户。因此,用户(或项目)之间相似度计算准确与否直接影响到整个系统的推荐质量。
国内外学者对协同过滤算法的相似性度量展开了一系列的研究。例如,Ahh[4]提出了修正余弦相似性(Adjusted Cosine Correlation)。Shardanand[5]考虑到评分的正负性,提出了约束皮尔逊相关系数(Constrained Pearson Correlation Coefficient)。Bobadilla[6]等人提出了将均值平方差异函数(Mean Square Difference)与Jacca⁃rd系数结合形成基于Jaccard系数的均方差异系数(Jaccard-based Mean Square Difference)。于金明[7]等人提出了一种基于 IPSS(IIF-based Proximity-Signifi⁃cance-Singularity)的协同过滤选法。于世彩[8]等人提出了一种基于项目类别和用户兴趣相似度融合(ICF_SI)的协同过滤算法。何顺[18]等人提出基于加权多融合偏好与结构相似度(MCF)的协同过滤算法。上述方法在数据稀疏时,其性能受到影响,推荐效果不够理想。
本文针对在数据稀疏的情况下相似度计算不准确的问题展开研究,充分考虑用户之间各种评分信息的差异,在原有相似度计算方法的基础上加入3个修正因子时间权重(详见2.1)、用户共同评分权重(详见2.2)以及用户平均分权重(详见2.3),可以在数据稀疏的情况下,获得比较好的度量用户的相似度,提高了推荐精度。
1 协同过滤算法
1.1传统的协同过滤算法
协同过滤推荐方法分为基于内存[9]和基于模型[10]两类,广泛应用于推荐领域[11-12],基于模型的方法是利用机器学习理论建立数学模型实现推荐[11],基于内存的方法属于启发式方法,包括基于项目的方法(Item-Based Collaborative Filtering)和基于用户的方法(User-Based Collaborative Filtering)[11]两种。当给定用户项目评分矩阵时,基于项目和基于用户两种方法原理类似,均使用近邻思想搜索出最相似的项目或用户列表进行推荐。
在协同过滤算法中,对目标用户产生推荐,主要分为三步:获取用户-项目矩阵、相似度计算并以此产生最近邻、进行评分预测[9]。常见的相似度计算方法有余弦相似度、相关相似性和修正的余弦相似性[11]。
(1)余弦相似性[14]。将用户评分数据看作n维向量,则用户之间的相似性用余弦函数来计算,若用户对某项没有评分,则默认将该项评分为0。将用户i和用户j在的评分看作两组向量,分别用a→和b→表示,则用户i、j的余弦相似度sim()i,j[13]为:

(2)相关相似性[11]。Pearson相关系数常是用来衡量两个数据集合之间的线性关系,则用户i和j之间的相似性sim(i,j)为:
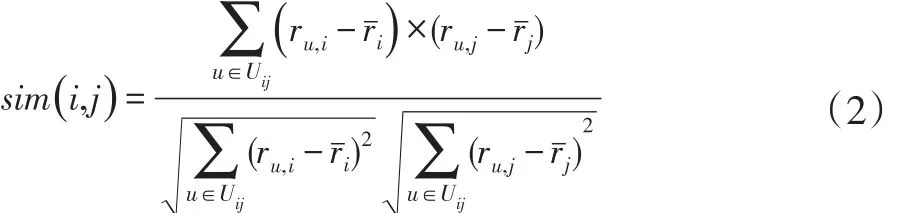
其中:ru,i用户u对项目i的评分,ru,j用户u对项目 j的评分,ri表示项目 i所有评分的平均值,rj表示项目j所有评分的平均值,Uij表示对用户对项目i和j评分的交集。
(3)修正的余弦相似性[11]。用户i和j之间的相似性sim(i,j)为:
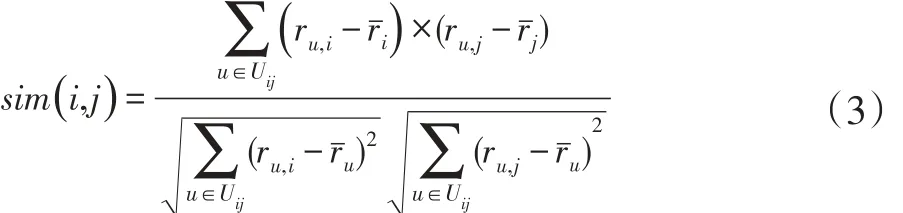
其中:Uij表示用户i和用户j共同评分项目集合,表示用户u所有评分的均值。
1.2传统相似度计算方法的缺陷
随着互联网的快速发展,网络中的信息呈指数级增长,用户数和项目数也随之飞快的增长,用户评分项目在总项目的占比一般不到1%[14],用户共同评分项目则少之又少,这将使得用户评分矩阵变得极度稀疏。在这种情况下,传统的相似度量值显然是不够准确的,进而带来是很难找到真正的最近邻居,推荐质量不高。本文就此分析以下三个方面。
(1)用户评分时间
传统的相似度计算,评分项目在计算过程中权重相同,并没有考虑到用户的兴趣爱好随时间的变化。例如,用户1、2、3有着相同的共同评分项目,但是用户1和用户2的评分时间和用户3的评分时间相隔很长,显然用户1和用户2比用户1和用户3更为相似,但应用传统相似度计算方法却可以得到相等的结果。
(2)用户共同评分
传统相似度的计算,忽略了近邻用户共同评分项目的影响,尤其是在评分数据疏的情况下,导致相似度计算偏差过大,以至于推荐精度不高。例如:由表1,显而易见u2和u3有2个共同评分项目,而u2和u4有3个共同评分项目,则u2和u3的相似度应小于u2和u4的相似度。然而,利用Pearson相关系数度量用户u2和用户u3及u4的相似度,可得 sim(u2,u3)为 1,sim(u2,u4)为 0.7895。
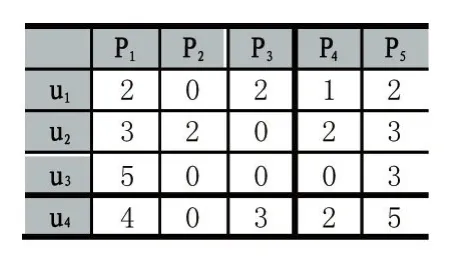
表1 用户评分矩阵
(3)用户平均评分
传统的相似度的计算,只是简单计算两个用户评分向量的线性相关性,却没有考虑到用户评分分数的差异。如表1利用Pearson相关系数度量sim(u1,u4)=1,说明用户u1和u4用相同的喜好,但是从表中数据来看对于项目P1和P5,用户u1评分都为2,用户u4为4和5,显然用户u4比较喜欢这两个项目。因此可以发现,传统的相似度计算方法对数值并不敏感。
随着用户评分矩阵的扩大,上述问题变得越来越严重,无法正确的找到真正相似的邻居,进而导致推荐质量的降低。
2 多因素融合的优化协同过滤算法
对于传统的相似度计算在数据极度稀疏,不能找到真正的邻居,进而导致推荐质量不高的情况下,本文将在传统相似度计算加入时间因子、用户共同评分因子以及用户平均评分因子进行改进和比较。
2.1时间因子
考虑到用户的兴趣随时间而改变,本文引入优化的sigmoid函数,作为用户相似度计算的时间权重,用户评分时间越接近,相似度也越高。计算公式如下:

其中,T(i,j)表示用户i和j评分时间权重,Uij表示用户i和j的共同评分集合,tiu和tju表示用户i和j对项目u的评分时间段。根据sigmoid函数特性,随着∣的增大,T(i,j)取值随之减小,取值范围为[0,1]。
2.2用户共同评分
传统的相似度计算对于用户共同评分并不敏感,尤其是在在数据评分矩阵非常庞大的情况下,忽略用户共同评分的影响,相似度的计算并不那么准确,因此本文引入Jaccard Similarity方法,公式如下:

其中,J(i,j)表示共同评分权重,Ii表示用户i评分项目集合,Ij表示用户j评分项目集合。当用户i和j共同评分项目数越多,相似度也越高。
2.3平均评分
为了提高推荐质量,在用户评分矩阵稀疏的情况下,Herlocker等人提出了改进用户评分分数的方法,对于那些和目标用户相似的用户,如果没有对共同评分项目进行评分,可以使用最近邻居用户的平均评分来填补[15],该方法在数据评分矩阵极端稀疏的情况下并不理想,也不能代表用户对该项目的评分,并且在最近邻居不准确的情况下,误差增大。因此,本文将用户的平均评分作为相似度计算的权重,公式如下:

其中,M(i,j)表示平均评分权重,Uij表示用户i和j共同评分项目,riu、rju表示用户i和j对项目u的评分。M(i,j)越大,说明用户i和j评分差异越小,相似度越高;反之,M(i,j)越小,说明用户i和j的评分差异越大,相似度也越低。
2.4改进的相似度计算方法
传统的协同过滤算法,在相似度计算上存在偏差,包括忽略了用户的兴趣随时间变化的因素、用户之间共同评分的因素以及用户评分差异等因素,导致推荐质量下降,尤其是在评分矩阵极度稀疏的情况下,推荐质量更是很差。本文融合以上因素提出一种改进相似度的算法 Isim(i,j),公式如下:
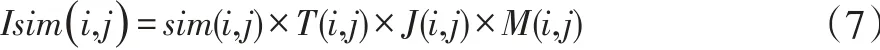
其中,sim(i,j)为传统的相似度计算方法,本文采用时下常用的相关相似性。
3 算法设计
对于改进算法设计如下:
输入:MovieLens数据集
输出:训练集预测评分与测试集的平均绝对偏差MAE
算法设计:
(1)指定训练集TrainFile和测试集TestFile;
(2)读取训练集,生成电影用户的倒排序表movie User;
(3)计算一个用户的平均评分;
(4)计算用户相似度
①计算有共同评分用户的评分时间差;
②计算有共同评分用户的共同评分项目数;
③计算基于平均评分、时间差异、共同评分项目数的相似性Isim()i,j;
(5)对用户相似度表进行排序;
(6)寻找用户的k个最近邻Nk={n1,n2,…,nk},并生成推荐结果,计算方法如下:
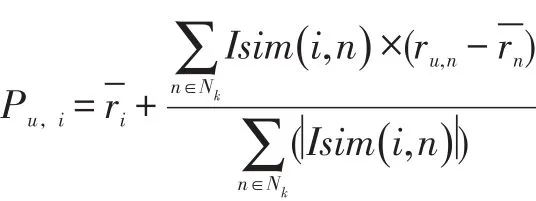
其中:Isim(i,n)表示用户i和n的相似度,、分别表示用户i和n的平均评分值;
(7)与测试集比较获得算法的准确度MAE。
4 实验结果与分析
4.1数据集
实验数据采用GroupLens小组提供的公开Movie Lens[16]数据集。针对研究需求的不同,MovieLens 小组提供多个版本数据集。本文采用943个用户对1682部电影10万次评分的小规模数据库,该数据库由用户看过的电影给予1~5的评分值形成,用户-评分矩阵密度为,可见用户评分矩阵十分稀疏。该数据集提供了5对训练集80%和测试集20%。数据集的数据包括用户名、电影名称、评分及评分时间。
4.2评估标准
平均绝对偏差(Means Absolute Error)和平均方根误(Root Mean Squared Error)[17]是衡量算法推荐精度的重要指标,本文采用MAE作为推荐算法准确性的衡量标准,MAE是通过计算训练集上的预测评分和测试集的实际评分进行比对,来确定推荐质量。MAE越大,推荐质量相应的也越差,公式定义如下:
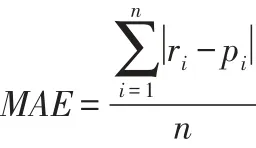
其中:{r1,r2,…,rn}为用户在测试集的评分,{p1,p2,…,pn}为用户在训练集上预测的评分,n为算法预测出评分集合的大小。
4.3实验结果
(1)最近邻居集
本文对MovieLens的5对数据进行实验,按照相似度形成邻居用户集,并对实验结果进行分析,如表2,邻居数目过多或过少都会影响推荐质量,因此需要确定邻居数目k的大小。试验中,分别取k=10,20,30,40,50,60,70,80,90,100,每个k值对应5个不同的数据集,并且将5次试验MAE的均值作为算法优劣的衡量标准。如表2,随着用户邻居的增大,MAE变化逐渐趋于稳定且当k=50推荐质量最好。
(2)和传统相似度计算方法相比
为了验证改进算法的推荐的准确性,本文以传统相似度计算方法与改进的相似度计算方法进行比较,在邻居数k=50的条件下每个计算方法在测试集和训练集上各自进行5次实验,如图1,可以发现,改进的相似度计算方法MAE比传统的计算方法要优秀,表明改进的相似度计算方法有利于推荐质量的提高。
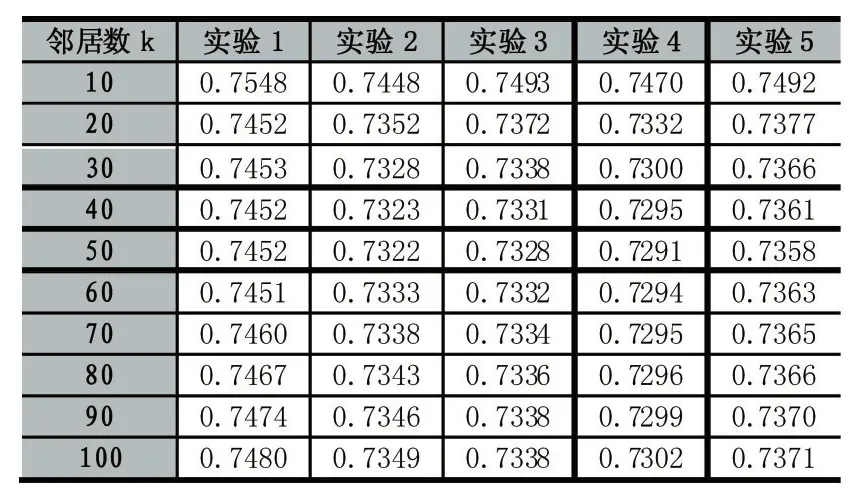
表2 不同邻居下的MAE
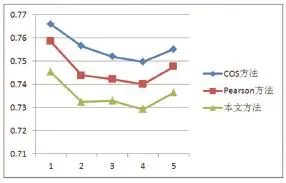
图1 与传统方法相比较
(3)不同方法下的MAE值
为了进一步检验本文提出相似性度量方法的有效性,本文与以下几篇论文的成果进行对比,邻居个数由上述实验结果选5到50,并选用MAE进行比较:本文算法比文献基于改进相似性度量的项目协同过滤推荐算法[7](Item Collaborative Filtering Recommendation Al⁃gorithm Based on Improved Similarity Measure,ICF_IP⁃SS),文献基于加权多融合偏好与结构相似度的协同过滤 算 法[18](Collaborative Filtering Algorithm Based on Weighted Multi-Fusion Preference and Structure Similari⁃ty,MCF,权重取ω=0.7),文献协同过滤的相似度融合改进算法[8](Improved Collaborative Filtering Algorithm of Similarity Integration,ICF_SI)的 MAE 都要低,表明改进的算法推荐精度高,算法的改进有效。
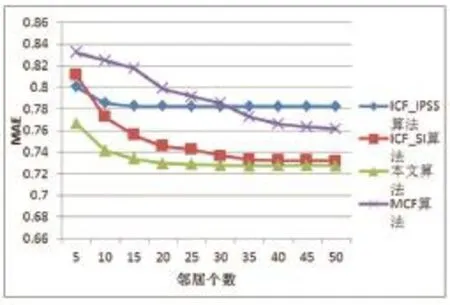
图2 本文方法与其他方法推荐精度对比
5 结语
本文分析了传统相似性度量方法的不足,针对这些不足,将时间权重、共同评分项目权重及用户平均评分权重引入用户相似度的计算中,提出了一种基于改进相似度的度量方法。该方法能够有效的度量相似度,解决了传统相似度计算方法存在的一些问题,并且实验结果表明,该方法有效地提高了推荐质量。

