巧设题组经历规律探索的全过程———《积的变化规律》教学设计

宋煜阳

【教学内容】

人教版四年级上册第四单元例3。

【教学设计】

一、寻找关联算式，形成题组感知规律

1.组织口算。

25+4= 32-5=

25×8= 16×5=

25×4= 32×5=

25×40= 56÷7=

2.选择研究算式，明确研究对象。

师：你觉得上面哪些算式与积的变化规律有关？

学生选择“25×4=100，32×5=160，25×8=200，25×40=1000，16×5=80”这几个乘法算式。

结合乘法算式回忆各部分的名称。

3.寻找关联算式，形成研究题组。

师：你会选择哪几个算式来研究积的变化规律？

（学生观察讨论）

教师针对学生的算式选择，整理为两大题组：

25×4=100 32×5=160

25×8=200 16×5=80

25×40=1000

师：为什么会把这三个算式分成一组，另外两个算式分成一组？

生：左边算式中都有一个因数25不变，右边算式中都有一个因数5不变。

师：我们今天来重点学习研究一个因数不变的情形下积的变化规律。

【设计思考：尽管学生早在一年级就开始学习找规律，但在本课之前都是局限于一行数据的观察（如找规律：1、3、5、7……），而积的变化规律需要借助一组算式加以观察发现。从一行数据转向一组算式，学生需要感知的强烈刺激。由于教材整体呈现了两组乘法算式，算式之间的关联感知刺激强度不够。为此，设计中通过选取关联算式形成研究题组，让学生初步感悟到积的变化规律需要在多个有关联的算式之间进行，同时明确了题组乘法算式的特点。】

二、题组内算式交互观察比较，形成规律猜想

1.集体观察题组中的部分算式，引导学生描述因数与积的变化现象。

师：观察下列题组中（1）、（2）两个算式，你有哪些发现？

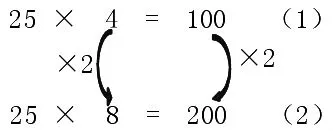
生：8是4的2倍。

师：因数从算式（1）中的 4怎样变化为算式（2）中的8？

生：因数从4到8，乘2。

（教师箭头标注“×2”）

师：还有什么发现？

生：200是100的2倍。

师：积从算式（1）中的 100怎样变化为算式（2）中的200？

生：积从100到200，乘2。

（教师箭头标注“×2”）

师：从算式（1）到算式（2），因数与积的变化情况你有什么发现？

生：因数25到25不变，另一个因数从4到8乘2，积从100到 200乘 2。

师：那从算式（2）到算式（1），因数与积又有怎样的变化呢？

梳理小结：在两道算式的比较中发现，一个因数不变，另一个因数乘2或除以2，积也乘2或除以2。

【设计思考：积的变化规律看似简单，实际上学生对题组的整体观察与联系描述存在困难。学生对题组的自主观察，往往停留于两道算式中单个元素（如某个因数或积）的观察比较，缺乏对因数、积两个元素变化的同步对应观察。同时，学生对因数与积的变化现象的描述缺乏逻辑性，像学生习惯表述的“4乘2得8”“100乘2得200”在本质上不是描述变化规律，而是在应用规律推算积的结果。针对这一困难，教学中引导学生采用“因数从4到 8，乘 2”“积从 100 到 200，乘2”的句式描述，并借助箭头标注，帮助学生建立起描述因数与积变化现象的话语系统。】

2.自主观察、描述分析题组中因数与积的变化现象，形成规律猜想。

师：比较下列题组中的算式（1）与（3）、（2）与（3），在学习单上算一算、标一标因数与积的变化情况，与同桌说一说变化现象。

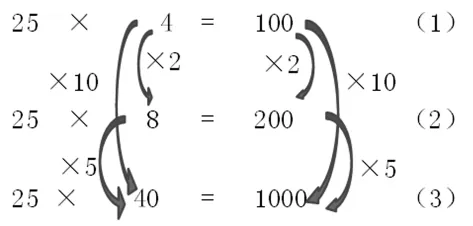
生：算式（1）到算式（3），因数25不变，另一个因数从4到40乘10，积从100到1000也乘10。算式（2）到算式（3），因数 25不变，另一个因数从8到40乘5，积从200到 1000也乘5。

师：那算式（3）到算式（1）、算式（3）到算式（2），它们的因数和积又是怎样变化的？

师：根据算式中因数与积的变化现象，你发现了什么规律？

生：一个因数不变，另一个因数乘几或除以几，积也乘几或除以几。

小结：在这一组算式中发现了积的变化规律，但这只是猜想，还需要在其他乘法算式中去验证。

【设计思考：通过题组观察比较、描述分析的模仿活动，学生经历了因数与积的变化现象的完整探索，为后续独立探索积累经验。在规律的发现、归纳中，让学生明确由例到类的猜想需要验证，才能确认结论。】

三、扩充和编写题组，举例验证，确认规律

1.出示题目：独立验证指定算式的规律。

验证要求：用箭头图标注说明下面两个算式中因数与积的变化情况；再根据题组自己写一个相关的乘法算式，并进行验证。

32×5=160 （1）

16×5=80 （2）

2.反馈。

（1）指定算式的验证。

反馈上述算式（1）（2）的验证情况，得出“第二个因数不变，第一个因数乘2或除以2，积也乘2或除以2”。

（2）扩充算式再验证。

反馈验证学生自己补充的算式（3），如“8×5=40”“16×10=160”“96×5=480”。先检查这些补充算式的计算结果是否正确，再验证算式（3）与算式（1）或算式（2）之间积的变化规律结论是否成立。

（3）独立编写题组验证。

学生自己独立按照题组举例，验证说明积的变化规律结论是否成立。指名反馈，发现结论成立。

3.总结规律。

师：像这样的例子举得完吗？在我们举的例子中，一个因数不变，另一个因数与积不是乘同一个数的，有吗？

生：4×0=0 与 8×0=0，因数 0不变，另一个因数从4到8乘2，积从0到0可以乘很多数，不一定是2。

师：在积的变化规律讨论中，因数不能为0，因数与积同时乘或除以一个数，0要除外。

小结：在规律验证中，既要找许多符合规律的例子，也要找不符合规律的反例。只要出现了反例就需要修订或推翻结论。

【设计思考：验证规律是规律探索活动的核心环节，既是对结论进一步明晰的过程，又是对不完全归纳推理思想方法的认识过程。通过题组中指定算式之间验证、根据题组自己扩充算式再验证、独立编写题组验证，由扶到放，学生掌握了题组编写和验证的方法，并形成了大量的例证。最后通过反例的讨论，修正了结论，也让学生对规律验证的全面性、科学性有了初步了解。】

四、题组练习，应用规律，内化提升

1.根据每组第一题给出的积，完成后面的计算。

第一组： 第二组：

37×3=111 24×15=360

74×3=（ ） 24×（ ）=120

37×27=（ ）（ ）×15=（）

第一组重点反馈：你是根据给出算式的哪个因数与积的变化规律来思考的？

第二组重点反馈“（ ）×15=（ ）”，结合学生练习中的“24×15”“24×45”“24×3”和“24×15”“48×15”“12×15”等材料形成题组进行观察，学生发现，这道开放题只要一个因数保持不变，另一个因数乘几或除以几，积也乘几或除以几，答案不唯一。

2.解决问题。

如果长不变，宽要增加到24米，扩大后的草坪面积是多少？

（学生独立完成后，用积的变化规律解释算式，图示验证）

【设计思考：第一题的题组一是“37×3”的组块训练，后两个算式围绕给出算式的两个因数进行了变化，防止学生对积的变化规律产生思维定势；题组二采用学生编题、形成题组的练习方式，要求学生从积的变化来思考因数的变化，并在学生给出的材料基础上再次形成题组，内化规律。第二题积的变化规律与生活中的面积问题相结合，拓宽了规律的应用范围。】