深刻理解概念实质方能落实核心素养
———兼评鲍善军、傅华峰两位教师《认识方程》一课
刘 松(特级教师)
一、曾经的困惑
十几年前,在一次教学研讨会上,笔者有幸应邀去上《列方程解决问题》一课。上课之初,自然提出三个问题:1.学过方程吗?2.什么是方程?3.方程是干什么用的?前两个问题,学生异口同声,对答如流,可第三个问题,全班50多位学生竟然面面相觑,无人作答。这不禁让笔者产生了深深的困惑。
再换个角度思考问题。小学阶段学习方程,仅从实用的角度分析,学习方程的重要目的之一就是应用,也就是列方程解决实际问题。众所周知,列方程解决问题有五大步骤,其中最核心的一步就是找出问题中包含的等量关系,然后列出方程。试想,倘若学生对“等量关系”和“方程”之间缺乏本质的理解,如何能深刻地把握列方程解决问题的关键所在?
《认识方程》是一节传统名课,教师大都是按照如下流程开展教学的:首先出示一架天平(实物或卡通模型),然后让学生在天平上摆物品,由此会列出许多式子,再让学生给式子分类,无论学生怎么分,教师两次追问,总能得出“含有未知数的等式”,至此,得出结论,而后判断练习,巩固概念,一节课结束。如此教学,非常流畅,甚至堪称经典,我们广大的一线教师照搬模仿即可。但正是如此经典,它却遗留了上述的困惑。何故?
于是,我不停地追问自己,《认识方程》一课究竟该教什么?又该怎么教?
二、真实的调研
2013年10月,笔者对本校五、六年级成绩最好的两个班共76名学生做了突然性的前测和后测。调查启示如下:
1.学生在上《认识方程》一课之前,对方程并非一无所知,对含有未知数的等式更不陌生。
2.对于尝试写方程,即便教师没教过,也有学生会写(且比例还不低)。
3.对于是否为方程的判断,学过和没学过的学生差异很大。测试中判断x-14>72是否为方程的错误率最高。六年级还有学生出错,为何?值得思考。
4.对于方程和等式的关系,即便六年级了,依然有学生出错,排除偶然因素外,不得不承认这恰恰是学生认知和学习的难点之一。
5.即便是六年级的学生,对“为什么会有方程(或者方程是怎么产生的、方程是干什么的)”也仅有不到8%的学生能回答到位。五年级更是全军覆没,有高达57.9%的学生空着没写。
三、可能的策略
1.引入自学。
从前测的数据中可以看出,学生在学习方程之前,对方程并非一无所知。即便是学生一无所知,对五年级的学生而言,在书上找到“含有未知数的等式叫方程”这句话很容易,且学生自一年级起就接触过诸如6+()=14等类的式子,对这句话的理解也不难。再退一步说,仅从字面上分析,学生自己也可以得出满足方程的两个必要条件:含有未知数和等式。既然如此,为什么不可以安排学生先自学课本呢?不先出现天平不行吗?
可能有的教师会质疑,传统的教法先出示天平好啊,况且许多版本的教材也是这样编排的。对此,笔者认同但并不完全赞同。且不说是“教教材”还是“用教材教”的问题。试问:对方程而言,究竟是天平的外形更重要还是背后的相等思想更重要呢?答案是显而易见的。既然天平背后的相等思想是关键,那我们为何不想尽办法让学生去感悟相等,何必仅仅拘泥于天平的形式呢?
2.颠倒叙述。
从前后测可以看出,在判断x-14>72是否为方程时,学生的错误率最高。五年级学生出错尚可理解,六年级学生依然出错,似乎不可原谅。但仔细想想,是否存在这样的可能,之所以有这么多学生出错,恰恰是教材编写所致。笔者认真查阅了国内五大版本的数学教材,对于方程的定义,都是这样描述的:含有未知数的等式叫方程。此话当然没错,但没错不代表就没有“副作用”。试想,如此偏正结构式的语句,关键核心词在哪?显然在后面,但首先映入学生眼帘的恰恰是含有未知数五个字。对部分五六年级的学生而言,是不是就先入为主,只记住“含有未知数”几个字了呢?这不就是俗称的第一印象效应吗?若如此,又该如何避免此类错误的出现呢?
为此,可在板书上做些改变。多年来,笔者对板书有一个基本的认知,板书如果仅仅是把书上的原话照抄在黑板上是没有多大意义的。如果一定要板书,则要对书上的原话做一些技术处理。当学生自学找到方程的定义后,在交流和追问的同时,黑板上留下了这样一个式子:“方程 =①等式 +②未知数”,而后反复引导学生叙述:含有未知数的等式叫方程。反过来,方程就是等式中含有未知数。如此,不仅可以很好地凸显方程的等式本质,还可以在一定程度上避免学生的上述错误。其实,对方程而言,如果可以比较的话,究竟是等式更关键,还是有未知数更重要呢?两者当然都重要,可以说各占50%。但笔者认为“相等”才是方程的灵魂所在。若果真如此,我们为何不好好地利用一下第一印象效应呢?
3.强化体验。
郑毓信教授曾言,小学数学概念教学有三要素:一要讲清概念是什么,二要说明为什么,三要厘清此概念与彼概念的区别和联系。其中第二个要素,往往被教师忽视,但这恰恰是学生最缺乏、最需要的。为什么会有方程?如何让学生体会到方程的产生?如何让学生感悟方程是现实世界中刻画相等关系的最美丽的模型这一重要思想?笔者认为,可尝试从源头上解决问题。为此,在学生自学完方程的定义、初步解读后,连续出示三个问题情境(如下图1、图2、图3),要求学生用一个数学式子表示情境中包含的相等关系。
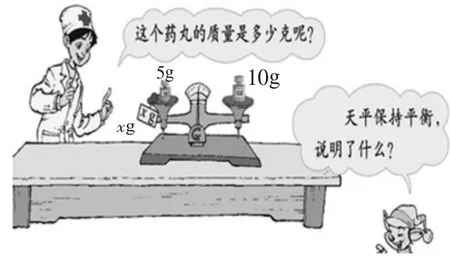
图1
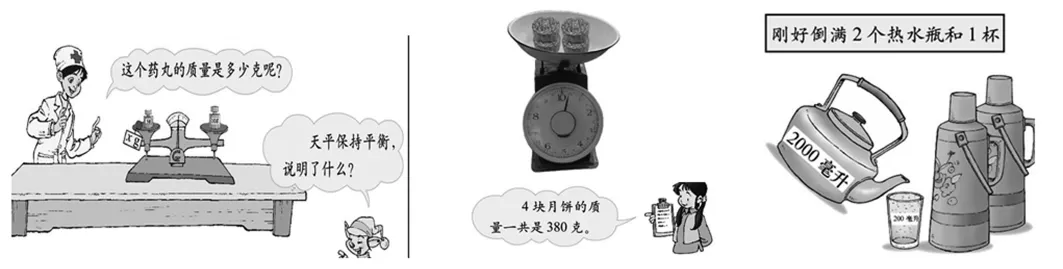
图2

图3
学生自然列出x+5=10,4x=380,2x+200=2000 三个式子,并板书在黑板上。针对每一个式子,反复引导学生互动追问:写的对吗?是方程吗?为什么是方程?如此,不仅有效地避免了教师出题、学生判断的木偶式学习方式,更为重要的是,学生在不断地用数学式子表达相等关系的过程中,自然体悟到了方程产生的原因。随着教师的调侃:他怎么一不小心又写出一个方程啊!学生就会逐渐地明白,方程其实并不神秘,它就是数学中表达相等关系的自然结果。为什么就决定了可以干什么,能干什么则取决于为什么。至此,方程的作用不言而喻,学生自己就可以说出方程即是表达相等关系的。
4.结构呈现。
针对方程和等式的关系这一难点。遵循思维可视化的原则,引导学生自己说出:方程是等式,等式不一定是方程。如何做到呢?可采用关键词追问策略。当学生板书完 x+5=10,4x=380,2x+200=2000三个方程后,追问:方程式还有别的可能吗?学生自然答出方程式有无穷多。然后再追问:即便是无穷多,这些式子都具有什么共同的特点?学生马上应答:等式、含有未知数。而后继续追问:是否有等式中不含有未知数的可能?反过来,是否有含有未知数但不是等式的可能?学生思考后板书。此刻,黑板上会有许多式子。教师则可趁热打铁继续追问:谁能用一个圈把黑板上所有的方程圈出来?谁还能用一个圈把黑板上所有的等式圈出来?……
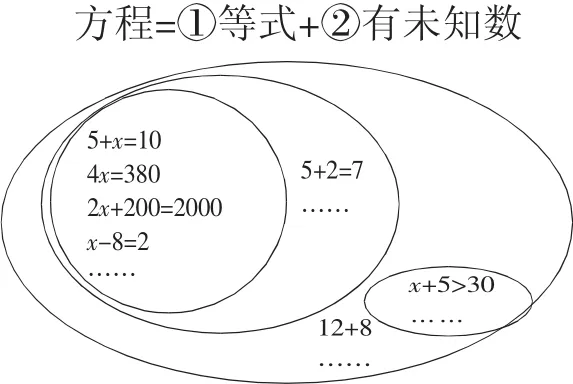
至此,黑板上会呈现一幅学生自己的“作品”,对着圈套圈提问:谁能发现什么?悟性好的学生即刻明白。因为有直观图的支撑,“方程是等式,等式不一定是方程”这两句话虽然没写出来,但意思已跃然纸上。而后在游戏练习中再植入12+8,追问:12+8应该放到哪个圈内?学生感觉都不合适,教师顺手在最外面再画一个大圈,板书:式子。至此,结构化板书大功告成。如此,学生不仅明白了方程与等式的关系,置身于数学式子的大家庭,还可以对方程也是一种数学表达式增加几分理解!
如上,《认识方程》该教什么、该怎样教就相对比较清晰了。
四、欣喜的现在
近年来,随着许多专家研究的深入,广大一线教师越来越清楚了方程意义的本质。正如鲍老师在课前思考中所言:方程的本质是什么?简单地说,就是左右两边数量相等,这不仅是方程概念的本质,也是列方程解决问题的依据。陈重穆教授曾撰文呼吁:“含有未知数的等式叫做方程”这样的定义要淡化,不要记,无须背,更不要考。关键是要理解方程思想的本质,它的价值与意义。张奠宙教授对方程重新定义:“方程是为了寻求未知数,在未知数和已知数之间建立起来的等式关系。”可见,“含有未知数的等式叫做方程”并非方程的严格定义,仅是一种朴素的描写,方程的意义不在于概念本身,而在于方程的本质特征:要“求”未知数,在未知数和已知数之间建立起来的等式关系。笔者更喜欢史宁中教授在《试论数学推理过程的逻辑性》一文中的详细解读,部分摘录如下:如果数学的定义不够清晰,就必然会影响数学命题的确切性,进而影响数学推理的有效性。作为例子,讨论一个现在仍然在使用的数学定义。在现行的中小学数学教科书中,关于方程的定义是这样的:称含有未知数的等式为方程。这个定义是属加种差的形式:等式是“属”、方程是“种”、含有未知数是“种差”。但是,含有未知数的等式未必就是方程,比如2x-x=x是一个含有未知数的等式,可这个等式表示的是符号运算,不是通常意义所说的方程。为什么会出现这样的情况呢?问题出在定义中的“种差”,在上述定义中的种差“含有未知数”这个性质不足以约束构成方程的等式。按照通常理解,所谓等式就是含有等号的数学式子,而等号具有两个功能:第一个功能是表示数值(包括符号)运算的传递性,第二个功能是表示等式两边的数量相等。因此,第一个功能只是在讲述一个故事,在这一个故事中数值(包括符号)是等价的、是可以递推的;第二个功能必须讲述两个故事,在这两个故事中两个数量的意义可以不同、但数量相等。方程利用的是等号的第二个功能,而反例2x-x=x利用的是等号的第一个功能,基于这个理由,含有未知数的等式就不一定是方程。因此,要构建方程的实质定义,除却未知数这个要素外,还必须在性质中或者说在种差中彰显等号的第二个功能。比如,可以把方程的定义表述如下:称含有未知数的表示等量关系的等式为方程。
综上,可以看出专家们的观点几乎是一致的。那就是,关于方程意义的教学,强调方程的等量关系比单纯强调方程中的未知数更便于学生理解和把握方程的本质。事实上,学生只有把握了概念本质,用顾沛教授的话说,才可能一通百通。如此教学,不仅可有效避免笔者曾经的困惑,更重要的是,还能使当下热议的学科核心素养有效落实。
鲍善军和傅华峰两位教师的教学设计虽不尽相同,但在突出等量关系上却是出奇的一致。虽然,傅老师的设计看似有些偏传统,但教学上好的经典当然也该继承,只要做到与时俱进,相机糅入新的形式、新的认知,更有利于学生学习即可。鲍老师的教学改革力度很大,教学效果不错,但略显遗憾的是,对于等号两个功能的解读,学生感悟可能不够深刻。记得郑毓信教授曾说:在算术中我们主要是从“操作(过程)的观点”看待“=”的,等号的左边表明我们应当实施哪些计算,得出的结果则应写在右边;也正因此,等式的两边就是不对称的,即有明确的方向性。与此不同,方程中对于“=”的理解则体现了这样一种观念:这主要代表了一种关系——等量关系,其本身也不具有任何的方向性。上述的观念对立并可被看成代数思维与算术思维的主要区别之一。也正因此,“方程”的教学就可被看成为我们在小学阶段初步渗透“代数思想”提供了重要契机。在教学中若能有意识地去引入一些“非标准变式”,如:将4x+7=35变形为4y+7=35,以及进一步变形为 4(2r+1)+7=35等等,另外一些更为复杂的变式:6=14-3x,6+x=14-7x,25+x=y-28等。从而帮助学生更好地实现由“过程(操作)性观念”向“结构性观念”的重要转变,也就是所谓的两个不同的故事,但数量相等,应该会有更深的体悟。
当然,由于《认识方程》是学生首次正式接触到了“方程”这样一个概念,因此,在第一课时就期望学生清楚地认识方程方法相对于算术方法的优越性应当说也完全不切实际。“代数思想”“方程观念”等需要循序渐进,逐步提升。但当练习时,有学生列出45+128=x,也认为是方程,教师不要回避则是必须的。
限于篇幅,不再赘述。两位教师及笔者的表述依然还有许多不足,恳请各位方家指正!

