P.C.变截面连续箱梁设计要点分析

朱亚龙，刘 胜

(湖南省公路设计有限公司，湖南 长沙 410000)

P.C.变截面连续箱梁具有安全、经济、美观、施工工艺成熟等特点，成为目前公路建设中很常见的桥型，但施工和运营过程中仍有部分箱梁箱体出现不同程度裂缝病害，裂缝的存在对结构的耐久性、安全度和正常使用都会产生十分不利的影响.究其成因，有设计富余量不足、施工质量控制不严、养护不到位等前期原因，也有使用超载、外界环境突变、意外事件等后期原因.

然而，结构设计作为控制病害的第一环，需要设计者具有一定的预见性，结合工程实践，分析以往工程病害的原因，总结经验教训，加强薄弱点的构造及配筋处理，提高安全储备，有效预防病害的出现.

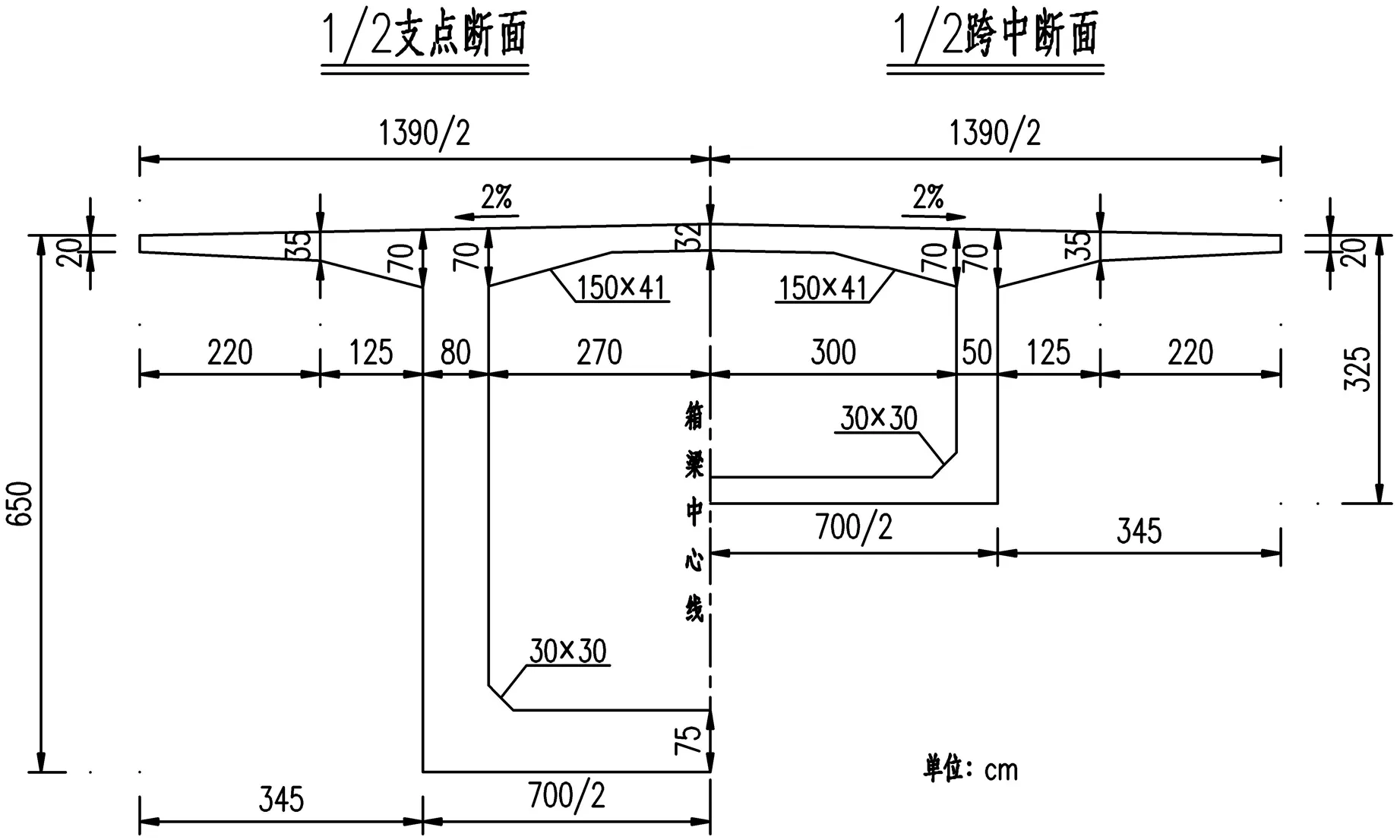
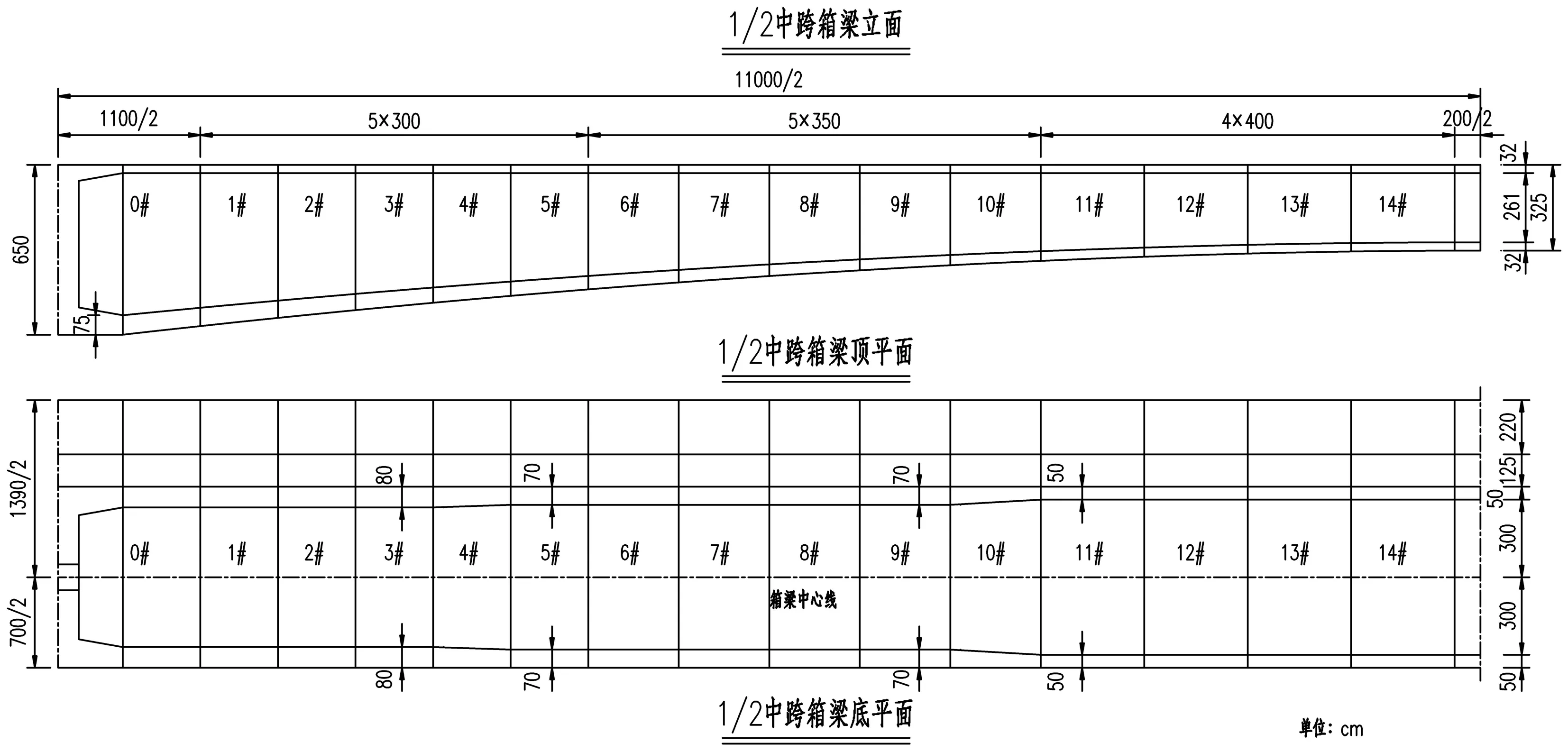
图1 箱梁一般构造

1 工程概况

某桥布置为(68+2×110+68)m四跨一联变截面连续箱梁.桥面全宽13.9m，箱底宽7.0m，两侧翼缘宽3.45m.

上部主梁采用单箱单室直腹板箱型截面，墩顶支点处梁高6.5m，边跨直线段及主跨跨中处梁高3.25m，梁高按1.8次抛物线变化.0#块和边跨现浇段采用支架现浇，其余节段均采用挂篮悬臂对称浇筑，按先边跨后中跨顺序合拢.主梁为纵、横、竖三向预应力结构，混凝土强度等级为C55，按全预应力混凝土构件设计.

2 纵断面设计

曲线形变高度连续梁支点及跨中高度经验公式为：支点高H=(1/16～1/20)L，跨中高h=(1/30～1/50)L.本桥设计取支点梁高6.5m(L/16.9)，跨中梁高3.25m(L/33.8)，梁高按1.8次抛物线变化；箱梁底板厚度为75cm(墩顶)～32cm(跨中)，厚度按1.8次抛物线变化；箱梁腹板厚度为： 80cm～70cm～50cm，具体变化情况见图1.

箱梁浇筑分段长度分别为11m+5×3m+5×3.5m+4×4m，边跨和跨中合拢段长2.0m，边跨现浇直线段长12.0m.主梁0#块长度一般控制在10.0～12.0m，过长则托架现浇施工不方便，过短则挂篮施工后支点不好立.悬浇分段长度一般控制在3.0～5.0m之间，尽量保证前、后段重量均衡变化，避免悬浇时梁段重量突变，造成应力集中.

3 横截面设计

3.1 顶板

顶板是桥梁直接承受汽车车轴荷载作用的部位，其病害一般出现在下缘，沿纵向开裂.设计时应根据横向桥面板计算确定其厚度及配筋，计算过程中横向预应力钢束的作用应做折减，并适当加强顶板下缘钢筋的配置.因为在实际施工过程中，顶板较薄，横向预应力钢束与普通钢筋交错布置，且操作空间有限，横向预应力钢束的“偏心距”较难精准控制，一旦偏差较大，很容易造成横向预应力不足，导致顶板下缘开裂[1].

3.2 底板

底板厚度由跨中至墩支点呈1.8次抛物线变化，设计时应满足受压区高度不超过底板厚度，保证腹板不受压.跨中底板钢束属于“凸”形束,与抵抗跨中正弯矩的理想形式相反,钢束的径向力容易引起沿底板束面发生径向撕裂[2].径向力大小根据底板各钢束永存应力换算得出，可按下列公式计算：

F=N·tan(a)/b

式中：F—作用于横向框架底板每根预应力钢束位置处的径向分力(KN/m)；

N—考虑预应力损失后每根底板预应力钢束的有效应力(KN)；

a—梁段之间的相对转角；

b—径向力沿桥纵向的平均分布宽度.

设计时根据横向环框计算确定底板厚度和配筋，其裂缝宽度建议控制在0.13mm以内.

3.3 腹板

腹板尺寸主要受斜裂缝(主拉应力裂缝)控制,斜裂缝一般发生在支点和四分点附近,并逐渐地向受压区发展和延伸[3].腹板尺寸主要通过主梁纵向抗剪计算确定，计算时一般不计竖向预应力作用(作安全储备)，也不考虑变高度梁段内附加剪应力的影响，计算结果需满足规范尺寸效应及抗剪承载力的要求.腹板厚度应结合主拉应力大小由支点向跨中逐步减小，使主梁主拉应力大小尽量均匀分布.腹板斜裂缝成因比较复杂，除受腹板厚度及配筋控制外，局部应力引起的徐变、腹板内外环境温度变化差异等影响也比较大，设计计算时建议将主拉应力控制在0.8MPa以内.

截面尺寸满足结构计算要求的同时还应结合预应力管道及钢筋位置综合考虑确定，注意钢筋(钢束)净保护层厚度以及预应力钢束锚端张拉的净边要求.

4 齿块设计

齿块作为钢束锚固点，承受局部应力较大，是病害经常出现的部位，其前后与主梁接触面一般为受力薄弱点，较易产生裂缝，如图2(a)中位置1、位置2处，产生的原因：位置1，端部强大的集中预加力作用下，在锚下的一定范围内，存在着很高的劈裂应力，容易造成开裂；位置2，在预应力钢束弯曲处产生径向压力，这个压力直接对钢束曲线内侧的混凝土产生作用，导致此处混凝土的崩出或剥落[3].设计时可从构造和配筋上加强处理，如图2(b).①将齿块主筋加强并与底板钢筋焊接成整体骨架；②锚下局部受压钢筋加强并伸入主梁腹板、底板锚固；③增大齿块顶角，调整预应力束圆曲线位置，使钢束径向力错开交接薄弱点.

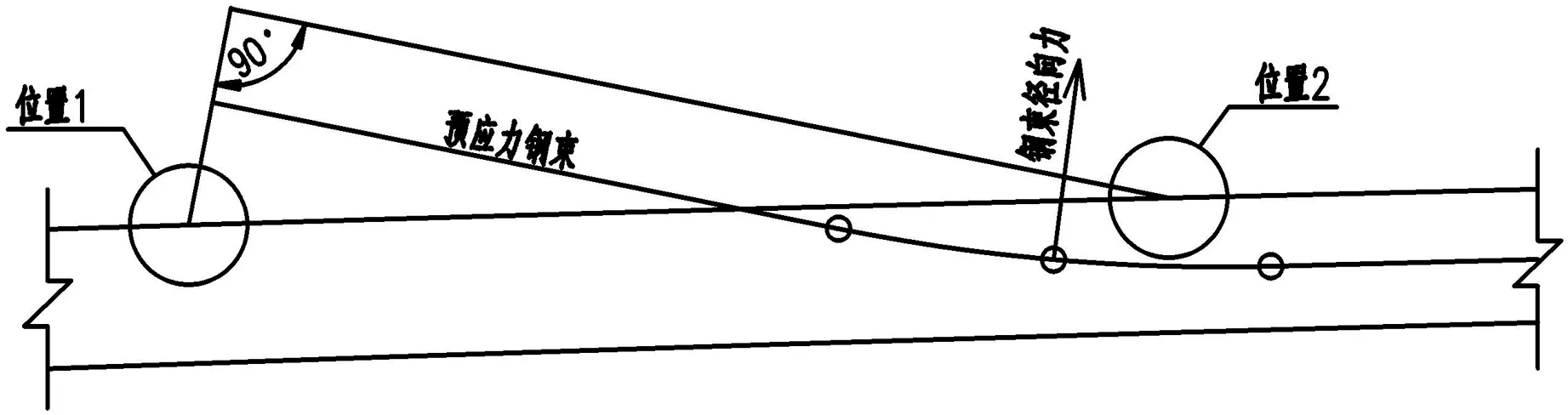
(a)

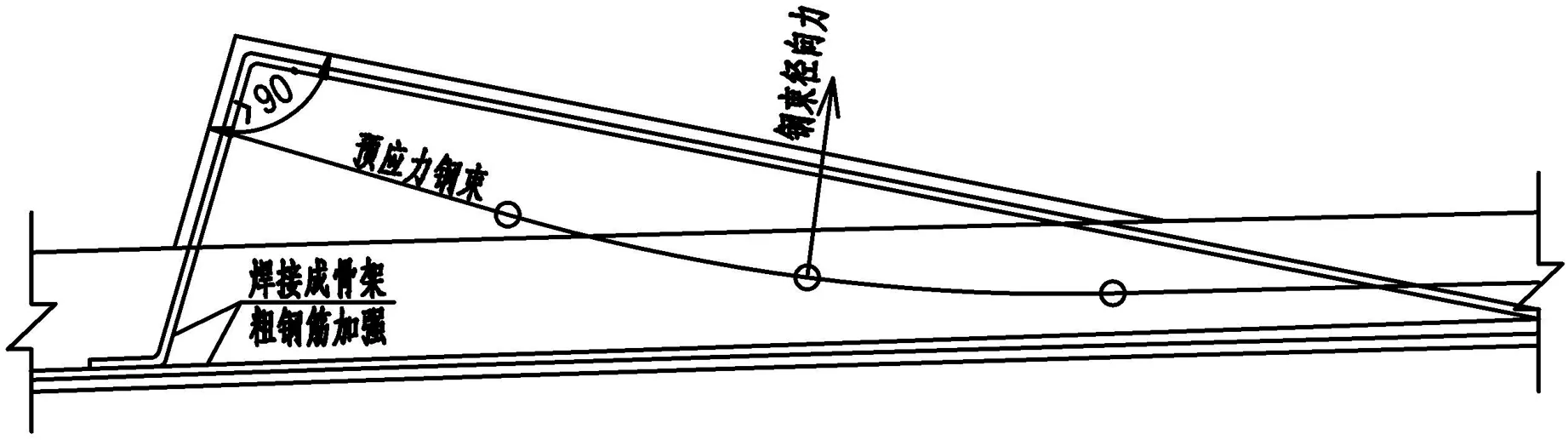
(b)

5 预应力管道布置

预应力管道布置是否合理直接关系到施工质量的控制.三向预应力应尽量与主梁钢筋避开，如图3所示腹板钢束置于顶板下层钢筋之下，错开倒角钢筋，避开竖向预应力封锚端；顶板钢束置于横向预应力之下，避开腹板箍筋及顶板下层钢筋；梗腋形式则依据T6、T7号钢束管道的保护层厚度来确定；底板钢束布置时应尽量靠近腹板，上层钢束B7、B3b置于底板上层钢筋之上，在底板厚度变化时，B7、B3b钢束也应随之对应变化.

图中仅示意墩顶及跨中标准断面布置，对于其他梁段，纵向钢束走向有平弯、竖弯，难免会与钢筋冲突，施工过程中可适当调整钢筋间距，并严格控制不得随意将钢筋截断.

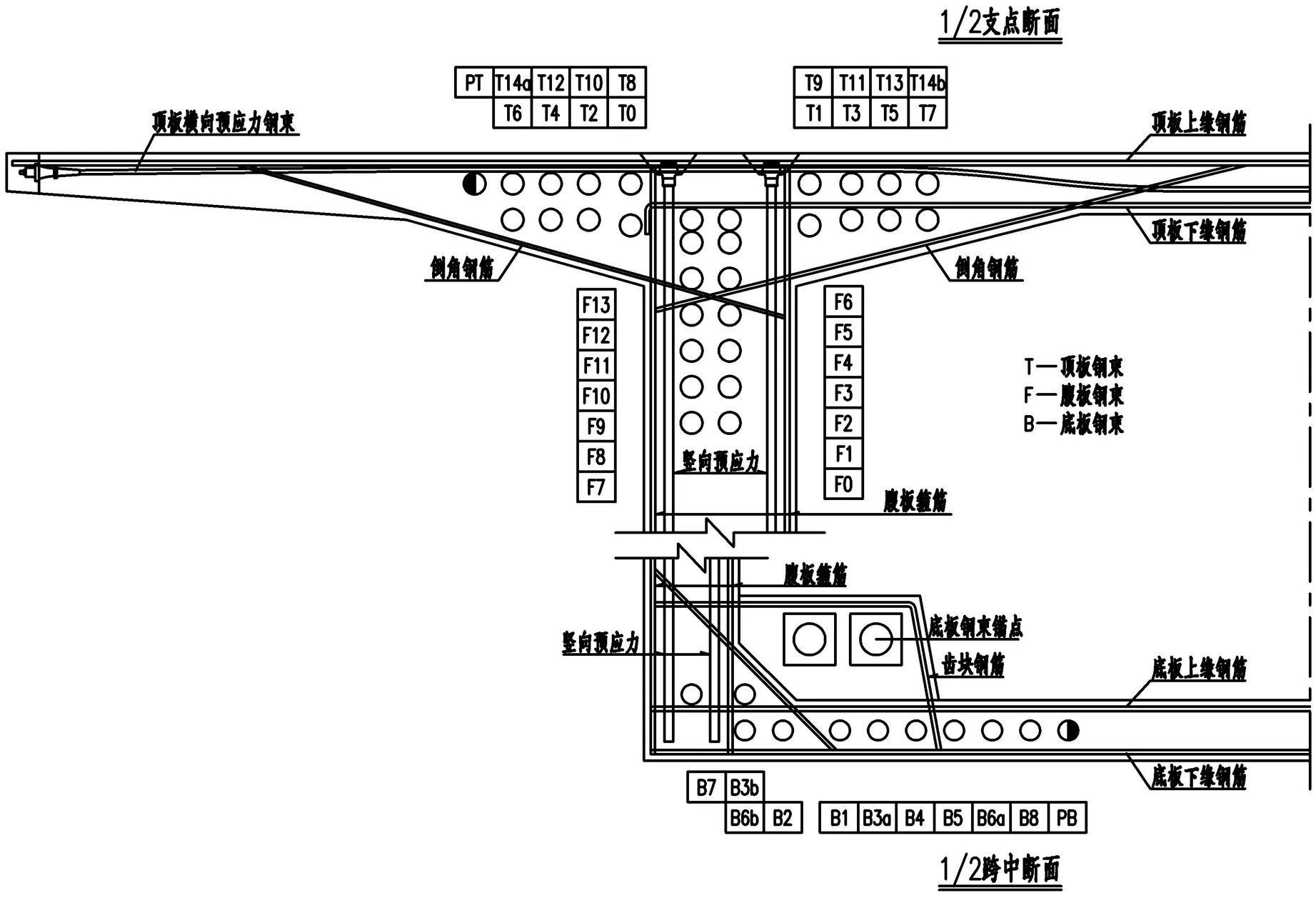
图3 箱梁索孔布置标准断面

6 结构计算

6.1 计算图式

结构采用“桥梁博士3.6”进行计算，按平面杆系理论，将上部主梁纵向共划分为122个单元，建立123个节点.按照实际施工过程共划分为18个施工阶段和1个使用阶段，求得构件在施工阶段和使用阶段时的应力、内力和位移，并根据规范中所规定的各项容许指标，验算构件是否满足规范规定的各项要求.

图4 计算模型

6.2 荷载分析

结构纵向受力只要包括：结构自重、汽车荷载、温度力、不均匀沉降、收缩徐变以及施工时人员、机具、挂篮等荷载.汽车荷载按公路-Ⅰ级车道荷载计入；温度力按体系整体温升25°、整体温降25°及梯度温度效应计入；不均匀沉降按边支0.8cm，中支1.2cm计入；收缩徐变按30年考虑；施工机具、人员及挂篮重量，一般按最大梁段重的0.35～0.45倍考虑.

6.3 计算结果验算(计算图示仅示半桥)

图5 主梁抗弯承载力(KN.m)

时间节点：刚成桥

时间节点：成桥30年后

时间节点：刚成桥

时间节点：成桥30年后

由于混凝土收缩、徐变会引起构件受拉区和受压区预应力钢筋的应力损失，主梁各计算指标值也会有一定范围的变化，所以，结构验算时应考虑一个时间阶段的结果而非一个时间点的结果.以本桥为例，计算刚成桥和成桥30年两个时间节点，就可以大致了解成桥30年内主梁承载能力、应力及钢束应力的变化情况，如下表1：

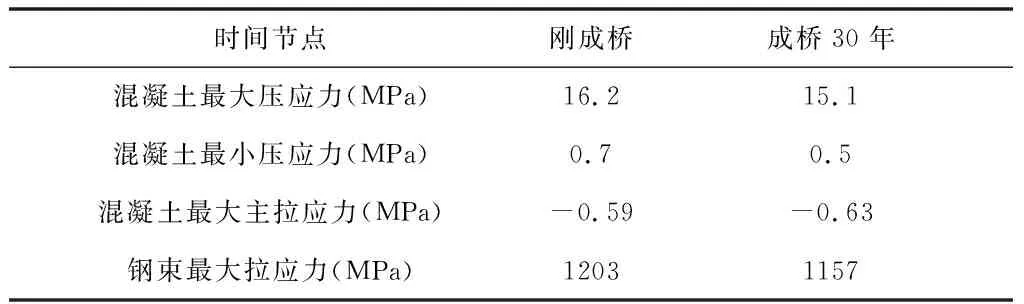
表1 计算结果对比表

通过以上对比表可知，在30年收缩徐变的影响下，混凝土最大、最小压应力及钢束拉应力会逐渐减小，而混凝土最大主拉应力会逐渐增大.

主要验算结果：

(1)主梁抗弯承载力设计值均大于作用效应组合设计值，且截面最小富余较大，承载能力完全满足要求.

(2)主梁正截面砼最大压应力为刚成桥时：σkc+σpt=16.2(MPa) ≤0.5fck=17.75 (MPa)，满足规范C55砼弹性阶段受压要求.

(3)主梁正截面砼最小压应力储备为成桥30年后：0.5(MPa)≥0(MPa)，满足规范全预应力砼受弯构件正截面抗裂要求.

(4)主梁斜截面砼最大主拉应力(支点位置失真)为成桥30年后：σtp=-0.63≤0.4ftk=-1.1(MPa)，满足规范全预应力砼受弯构件斜截面抗裂要求.

(5)受拉区预应力钢筋的最大拉应力为刚成桥时：σpe+σp=1203MPa≤0.65fpk=1209MPa；满足规范预应力材料弹性阶段的使用要求.

通常，设计采用平面杆系有限元进行计算,假定箱梁全截面受力,顶、底板的压应力分布均匀.事实上，对于预应力混凝土连续箱梁，由于剪力滞和大吨位钢束锚固的影响，箱梁各截面的应力分布是不均匀的(如腹板附近的顶底板正压力相对较大)[1].在设计过程中应对截面正应力上下限进行控制，保持一定的安全储备，否则极易导致箱梁应力值超限，出现腹板和角隅裂缝、顶底板沿管道开裂等质量事故.

7 结语

本文以一实际工程设计为背景，主要介绍了P.C.变截面连续箱梁在尺寸拟定、预应力钢束布置、计算控制等方面一些经验总结.但仍有许多方面没有涉及，如纵向下弯腹板钢束布置、预应力钢束张拉和压浆工艺、温度效应、地震效应等都很值得探讨.

随着国内经济的高速发展，交通运输业也愈发繁忙，超载超限行为屡禁不止，许多桥梁已超负荷运转，病害日益突现.近年来国内行业规范也在不断的完善，不断的提高标准.作为设计工作者，我们应该具备一定的前瞻意识，高标准严要求，结合施工实践，不断总结经验，优化设计，做精品工程.使我们建设的桥梁在面对超载、偏载、极端气候条件等不利效应叠加时，仍能满足正常使用的要求.