Free Energy Change of Micelle Formation for Sodium Dodecyl Sulfate from a Dispersed State in Solution to Complete Micelles along Its Aggregation Pathways Evaluated by Chemical Species Model Combined with Molecular Dynamics Calculations

YOSHII Noriyuki , KOMORI Mika , KAWADA Shinji , TAKABAYASHI Hiroaki ,FUJIMOTO Kazushi , OKAZAKI Susumu

1 Center for Computational Science, Graduate School of Engineering, Nagoya University, Nagoya 464-8603, Japan.

2 Department of Applied Chemistry, Nagoya University, Nagoya 464-8603, Japan.

Abstract: Surfactant molecules, when dispersed in solution, have been shown to spontaneously form aggregates. Our previous studies on molecular dynamics(MD) calculations have shown that ionic sodium dodecyl sulfate molecules quickly aggregated even when the aggregation number is small. The aggregation rate, however, decreased for larger aggregation numbers. In addition, studies have shown that micelle formation was not completed even after a 100 ns-long MD run (Chem. Phys. Lett. 2016, 646, 36). Herein, we analyze the free energy change of micelle formation based on chemical species model combined with molecular dynamics calculations. First, the free energy landscape of the aggregation, ∆G†i+j, where two aggregates with sizes i and j associate to form the (i + j)-mer, was investigated using the free energy of micelle formation of the i-mer, Gi†, which was obtained through MD calculations.The calculated ∆G†i+j was negative for all the aggregations where the sum of DS ions in the two aggregates was 60 or less. From the viewpoint of chemical equilibrium, aggregation to the stable micelle is desired. Further, the free energy profile along possible aggregation pathways was investigated, starting from small aggregates and ending with the complete thermodynamically stable micelles in solution. The free energy profiles, G(l, k), of the aggregates at l-th aggregation path and k-th state were evaluated by the formation free energyfree energy of mixing where ni(l, k) is the number of i-mer in the system at the l-th aggregation path and k-th state, with . All the aggregation pathways were obtained from the initial state of 12 pentamers to the stable micelle with i = 60. All the calculated G(l, k) values monotonically decreased with increasing k. This indicates that there are no free energy barriers along the pathways. Hence, the slowdown is not due to the thermodynamic stability of the aggregates, but rather the kinetics that inhibit the association of the fragments. The time required for a collision between aggregates, one of the kinetic factors, was evaluated using the fast passage time, t FPT.The calculated t FPT was about 20 ns for the aggregates with N = 31. Therefore, if aggregation is a diffusion-controlled process, it should be completed within the 100 ns-simulation. However, aggregation does not occur due to the free energy barrier between the aggregates, that is, the repulsive force acting on them. This may be caused by electrostatic repulsions produced by the overlap of the electric double layers, which are formed by the negative charge of the hydrophilic groups and counter sodium ions on the surface of the aggregates.

Key Words: Free energy change; Aggregation pathway; SDS; Micelle; Molecular dynamics calculation

1 Introduction

Stability of micelles in solution is of great interest in basic chemistry including the fields of amphiphilic molecular aggregates, such as biomolecules. A large number of theoretical and experimental studies have been conducted so far1–6. First,regarding the stability of micelles, Tanford1and Israelachivili et al.2proposed models based on the attractive force between hydrophobic groups and repulsive force between hydrophilic groups. Further, Everette developed a model3that incorporates micellar surface contributions. In addition to these studies,Blankschtein et al.4, Oxtoby et al.5, and Chandler et al.6proposed detailed thermodynamic and statistical mechanical models that include intermolecular interactions of surfactant molecules. It is now possible to accurately reproduce the free energy, aggregation number, and critical micelle concentration(CMC) of the micelles.

From the viewpoint of computational science, the free energy of micelle formation and micelle size distribution have also been investigated by molecular dynamics (MD) calculations7.Furthermore, using all-atomistic and coarse-grained MD/Monte Carlo calculations, the aggregation process of surfactant molecules dispersed in water was examined to evaluate the size distribution of the aggregates8–22. We also performed non-equilibrium MD calculations for anionic sodium dodecyl sulfate (SDS), cationic dodecyltrimethylammonium chloride(DTAC), zwitterionic dodecyldimethylamine oxide (DDAO),and nonionic octaethylene glycol monododecylether (C12E8)surfactant molecules with an alkyl chain of 12 carbon atoms and n-dodecane molecules23,24. The aggregation number, i, of C12E8and n-dodecane increased in proportion to the elapsed time t. This indicates that the aggregation obeys the Lifshitz-Slyozov (LS) law25and is a diffusion-controlled process. In contrast, the aggregation showed non-LS behavior for SDS and DTAC (I ∝ t0.3), and for DDAO (I ∝ t0.6).

Among them, formation of stable micelles was completed smoothly for nonionic C12E8 within 50 ns. However, it was not completed for ionic SDS and DTAC in spite of the 100-ns-long MD calculations where a few aggregates composed of several tens of surfactant molecules remained unassociated with each other in solution.

In this study, thermodynamic stability is evaluated for the SDS aggregates of intermediate size on the way to a complete micelle. A molecular structure of the SDS is shown in Fig. 1. If there are a high-free-energy aggregate on the way to the complete micelle, it takes long time for the aggregates to reach the complete micelle. In order to investigate possibility of such unstable aggregates, all aggregation pathways were examined and free energy changes along these pathways were evaluated based on the chemical species model. There, we use free energy of formation of the aggregates which were obtained in our previous study7based on thermodynamic integration method and MD calculations. We also investigated a kinetic factor in the association process. For the association to proceed, the aggregates need to collide with each other by diffusion. In the present study, the collision rate was estimated by the fast passage time26based on the Smolchowski equation. By evaluating the thermodynamic stability of the aggregates together with the collision rate of the aggregates, we can obtain the microscopic rate determining factors that control the association process of the aggregates.

2 Theory

In our previous study, free energy of formation was evaluated as a function of aggregation number7for SDS aggregate using MD calculations. In the present study, the free energy of aggregation was evaluated for all possible SDS fragments using our previous result.

2.1 Chemical species model

Free energy of aggregation of i surfactant molecules (an“i-mer”) from monomers can be evaluated based on the chemical species model. In this model, aggregates with different aggregation numbers are regarded as different chemical species. An isolated surfactant molecule in vacuum was regarded as the reference state. Letbe the chemical potential of the fully hydrated i-mer in the infinite dilute solution. Since there are no aggregates other than i-mer, the mole fraction Xiof the i-mer is unity. Then, the chemical potential, μi, of the i-mer can be expressed by

where kBis the Boltzmann constant, T the absolute temperature,and γithe activity coefficient.

For the system composed of Nii-mers and Nwwater molecules, free energy of the total system can be described by

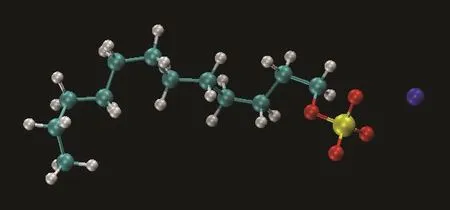
Fig. 1 The molecular structure of SDS.Yellow: sulfur atom, red: oxygen atom, cyan: carbon atom, gray:hydrogen atom, and blue: sodium ion. Color online.

where μwis the chemical potential of water.

2.2 Equilibrium mole fraction of i-mer

We assume that the aggregation reaction of one (i − 1)-mer and one monomer to form one new i-mer occurs reversibly. We also assume that other aggregates in solution do not change.Then, the free energy change, ΔG, is expressed using Eqs. (1)and (2) as

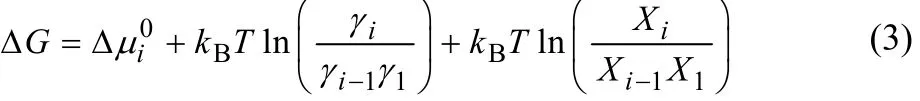
If the system is in equilibrium, ΔG = 0. Then, the mole fraction,, in the equilibrium state satisfies,

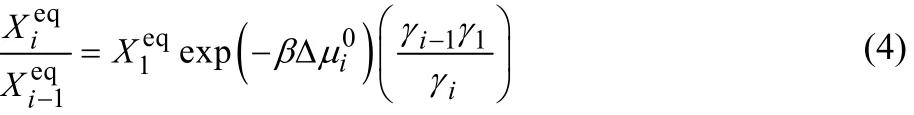
as easily derived from Eq. (3).

2.3 Activity coefficient of i-mer

Debye-Hückel (DH) theory is used to evaluate the factorin Eq. (4). According to DH theory, lnγi∝i2for the activity coefficient γiof ions with i charges27. Using this expression, we obtain the relationship

where the coefficient α was determined such that it reproduces the experimental critical micelle concentration (CMC)7.

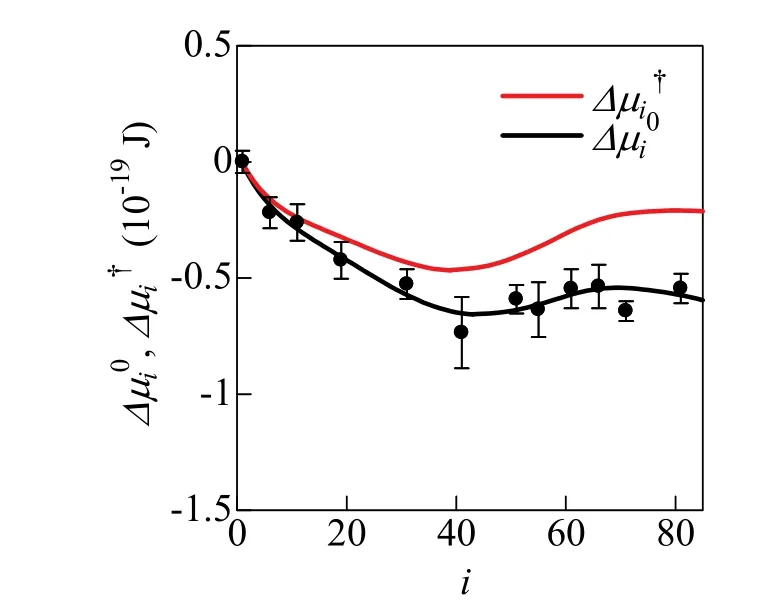
Fig. 2 Δμi0 and Δμi† as a function of aggregation number i.The value of Δμi0 obtained from MD calculation is given in Ref. 7. The black solid line

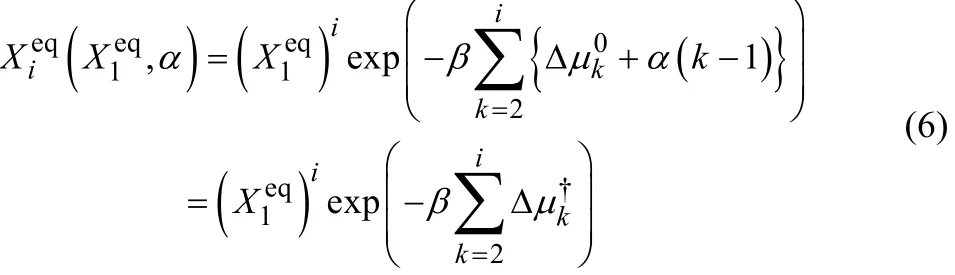
There are several definitions of CMC using. Here, we adopted the definition thatsatisfies the condition of

at CMC28, where the total number of molecules belonging to the aggregate of a certain aggregation number i (≠ 1) is the same as the total number of molecules of the monomer. Then,we can determine, and α numerically using Eqs. (6)–(8). In the previous study7, α = −4.5 × 10−22J and X1eq=0.00015 were obtained, and an aggregation number of i = 57 gave the maximum value of

2.4 Free energy of formation of the aggregates

Excess free energy of formation G†iof the i-mer is the sum of the free energy of aggregationthe contributionof the activity coefficient.can be expressed using Δμk†defined by Eq. (6) as

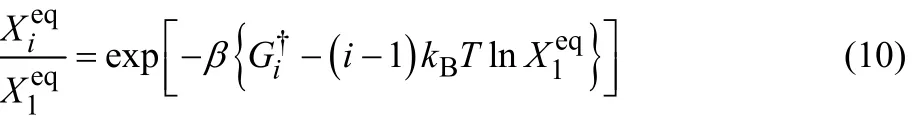
Then, we can obtain the information about the size distributionof the i-mer by comparingwith (i − 1) kBT ln Xieqat each i.

Table 1 Fitting coefficients, ak, of Δμi0, where Δμi0 is approximated as

Table 1 Fitting coefficients, ak, of Δμi0, where Δμi0 is approximated as

1 ≤ i ≤ 66 66 ≤ i ≤ 80 a0 4.11 × 10−21 7.11 × 10−21 a1 −5.51 × 10−21 −4.81 × 10−21 a2 3.73 × 10−22 1.21 × 10−22 a3 −1.73 × 10−23 −1.21 × 10−24 a4 4.24 × 10−25 4.00 × 10−27 a5 −5.31 × 10−27 −a5 3.24 × 10−29 −a7 −7.65 × 10−32 −

The excess free energy of aggregation,where two aggregates with sizes i and j associate to form the (i + j)-mer can be given by

Then, free energy of aggregation, ΔGi+j, may be obtained by adding ideal free energy of mixing

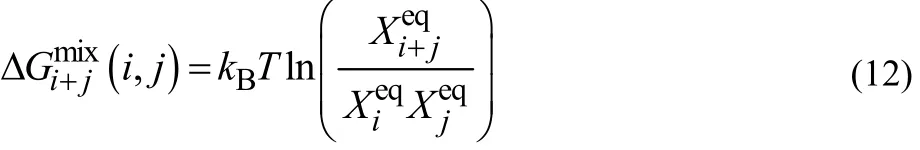
This determines whether the aggregation actually goes forward or not.

to the excess free energy of aggregation, Eq. (11), as

3 Results and discussion

In this section, free energy of aggregation of an i-mer and j-mer to form (i + j)-mer is presented. The free energy profile is also investigated along aggregation pathways, and then,kinetics in the final stage of the aggregation is discussed.

3.1 Free energy of micelle formation

As shown in Fig. 2, free energy of micelle formation,andrapidly decrease with increasing i for i ≤ 10. This stability is caused by the increase of coverage of the aggregate surface by hydrophilic groups with increasing aggregation number29. In contrast, the instability for i ≥ 40 is due to the decrease of the distance between hydrophilic groups30.

Fig. 3 shows the free energy of formation,, of the i-mer calculated by Eq. (9). Theshows an inverse S-shaped function with an inflection point near i = 40 wherein Fig. 2 has a minimum. The shape of thiscurve is similar to the reported model functions of the free energy of micelle formation2,3; it is convex upward for 1 ≤ i ＜ 40 and convex downward for 40 ≤ i ≤ 80. Now,is constant in the range of 0 ＜＜ 1, such that (i − 1) kBT lnis a monotonically decreasing linear function of i, as shown in Fig. 3. Probability that the i-mer is found in the system is determined by the relative magnitude of bothand (i − 1) kBT ln, as shown in Eq. (10). Thus, the aggregates with 1 ≤ i ＜ 40 are not found because of the condition,− (i − 1) k B T ln＞ 0. In contrast, the aggregate with 40 ≤ i ≤ 80 must be found in the system because of the conditionin Fig. 3 shows such tendency, giving a correct micelle size distribution.

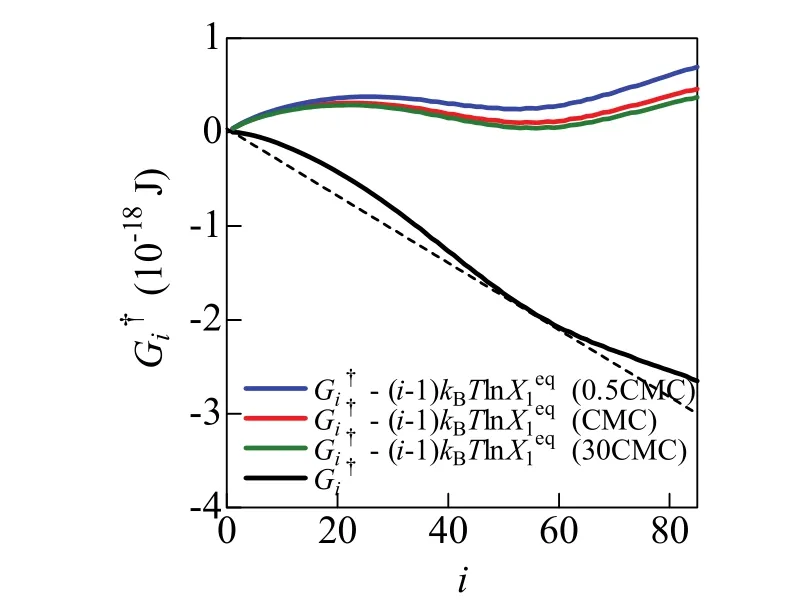
Fig. 3 Aggregation number i dependence of G†i − (i − 1) k B T ln X1eq. at 0.5CMC, CMC, and 30CMC are depicted by the blue, red and green lines, respectively. The black dashed line represents (I − 1)k B T ln at CMC. Color online.

In Fig. 3, there is a broad high free energy region around i =20. The aggregation between the two aggregates with similar sizes (i ≈ 20) hardly occurs at CCMCbecause the probability that the aggregates with i ～ 20 are found in the system is much smaller than that with i = 1 and 57. This is consistent with the Aniansson-Wall model31, where aggregation proceeds through the sequential reaction in which the aggregate size increases by addition of monomers.

3.2 Free energy of aggregation of the i-mer and j-mer

Fig. 4 shows a free energy landscape of aggregation,of an i-mer and j-mer given by Eq. (11).is negative for all i and j where the two aggregates satisfy i + j ≤ 60. The aggregation under this condition proceeds thermodynamically.In particular,becomes a large negative value when the two aggregates are of similar size with i ≈ 30. This is because,as shown in Fig. 3, the aggregates with i ≈ 30 are greatly unstable, while the aggregates with i ≈ 60 are quite stable.

In contrast, in the aggregation of the large fragments of i ≥60 (for example, two 60-mers are fused into one to form a 120-mer), ΔG†i+jhas a large positive value. In such an aggregation, the hydrophilic groups in the formed aggregate become close to each other on the aggregate surface30. It is quite unstable.

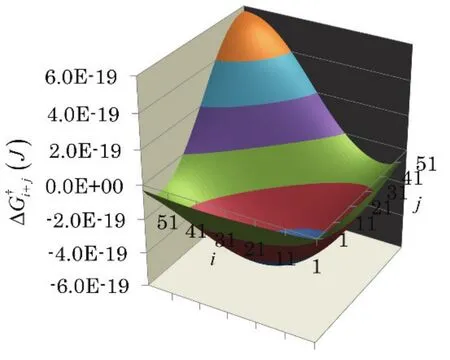
Fig. 4 Free energy landscape, of formation of an (i + j)-mer from i-mer and j-mer.

3.3 Free energy profile along possible aggregation pathways

We consider free energy profile along possible aggregation pathways from randomly solved structure to complete spherical micelles. The aggregation pathways are generated randomly according to the procedure given in Fig. S1. Here, l is the index of independent aggregation path, and k represents the state of the system. Then, the free energy profile, G(l, k), was evaluated usingby,

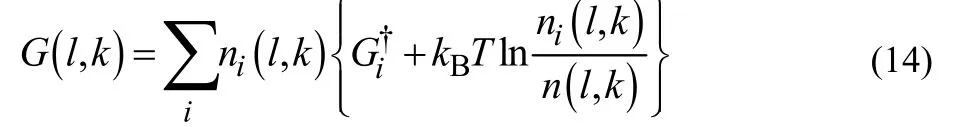
where ni(l, k) is the number of i-mer in the system at l-th aggregation path and k-th state.number of aggregates in the system. The free energy of mixing,Gmix(l, k), was evaluated by,

We started with 12 pentamers as an initial state because the number of aggregation paths from 60 monomers is too large to calculate. This initial state is reasonable because at the early stage of aggregation simulation from the randomly dispersed molecules, the monomers quickly associated to form small fragments with a several molecules such as pentamers. Totally 39700 aggregation paths were investigated. 800 randomly chosen profiles, G(l, k), and the contribution of Gmix(l, k) are plotted in Fig. 5a.

G(l, k) decreases monotonically with increasing k at all l. The free energy does not increase with the growth of the aggregates.Further, the absolute value of Gmix(l, k) is several tens of kJ·mol−1, whereas that of G(l, k) is several hundreds or one thousand kJ·mol−1. It is more than one order of magnitude largerG(l, k).

Fig. 5b shows increment of the free energy ΔG(l, k) = G(l, k) −G(l, k − 1) along the path. It is noted that they are all negative values. Although the positive values were found that in several ΔGmix(l, k) = Gmix(l, k) − Gmix(l, k − 1), the values are in the order of several kJ/mol, their contributions to ΔG(l, k) being quite limited. As a result, ΔG(l, k) is in the range of −50 to−270 kJ·mol−1. Thus, no barrier is found in the free energy profile from the initial state to the complete spherical micelles.

3.4 Aggregation simulation

Next, free energy change during spontaneous aggregation of the fragments was investigated based on the aggregation simulation. The detail of the aggregation simulation is described in the supporting information.

Snapshots of SDS aggregates in an aggregation simulation are shown in Fig. 6. From the trajectory of the aggregation simulation, fragments were identified using the intermolecular bond between the DS ions. The contact area between the hydrophobic parts of the two DS ions was used to define the bond between the DS ions. Voronoi polyhedra were defined using all atoms except for hydrogen. The surface of the DS ion was defined using the Voronoi polyhedra. When the contact area of the two DS ions is greater than a threshold value, the two DS ions were regarded as bonded. From the contact area distribution of two DS ions in the stable SDS micelle, the threshold was set to be 0.05 nm223.

Results of the aggregation simulation are shown in Fig. 7.The largest aggregation number is plotted in Fig. 7a for independent six MD runs. The aggregates with i = 10–20 were quickly formed within several tens of nanoseconds. However,the aggregation did not proceed more. Four largest aggregation numbers are plotted as a function of t in Fig. 7b for one trajectory, green one in Fig. 7a. At t = 30 ns, three aggregates with aggregation numbers of 12, 19, and 29 were formed.However, their aggregation numbers hardly changed until t =100 ns.

The time evolution of the maximum aggregation number presented here is similar to that of aggregation simulation performed using different potential parameters (CHARMM 36)23.

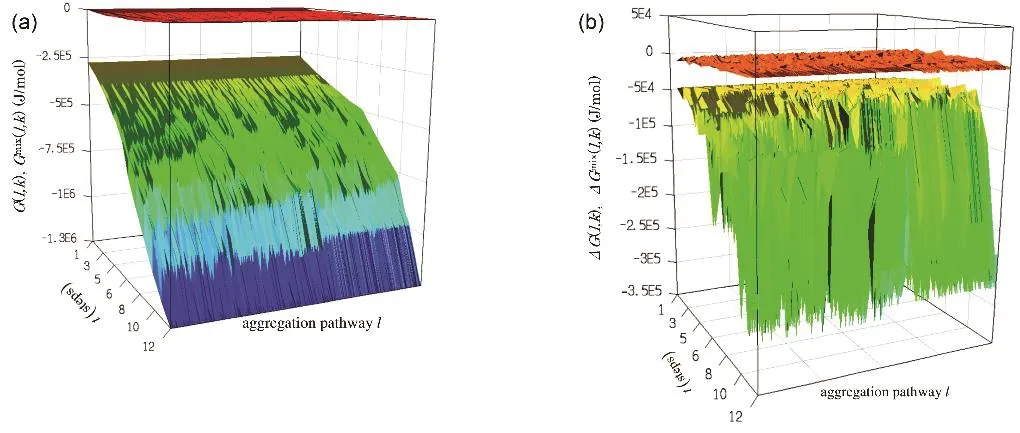
Fig. 5 Free energy profile G(l, k) (lower plot of (a)) and G mix(l, k) (upper plot of (a)), and ΔG(l, k) (lower plot of (b)) and ΔG mix(l, k) (upper plot of (b))along the aggregation pathways.Note that the scales on the vertical axes are different between (a) and (b).

Fig.6 Snapshot of SDS aggregates in solution at elapsed time (a) t = 0 ns, (b) 7 ns, (c) 50 ns, and (d) 100 ns.Colors for atoms are the same as in Fig. 1. Water molecules are not depicted for clarity.

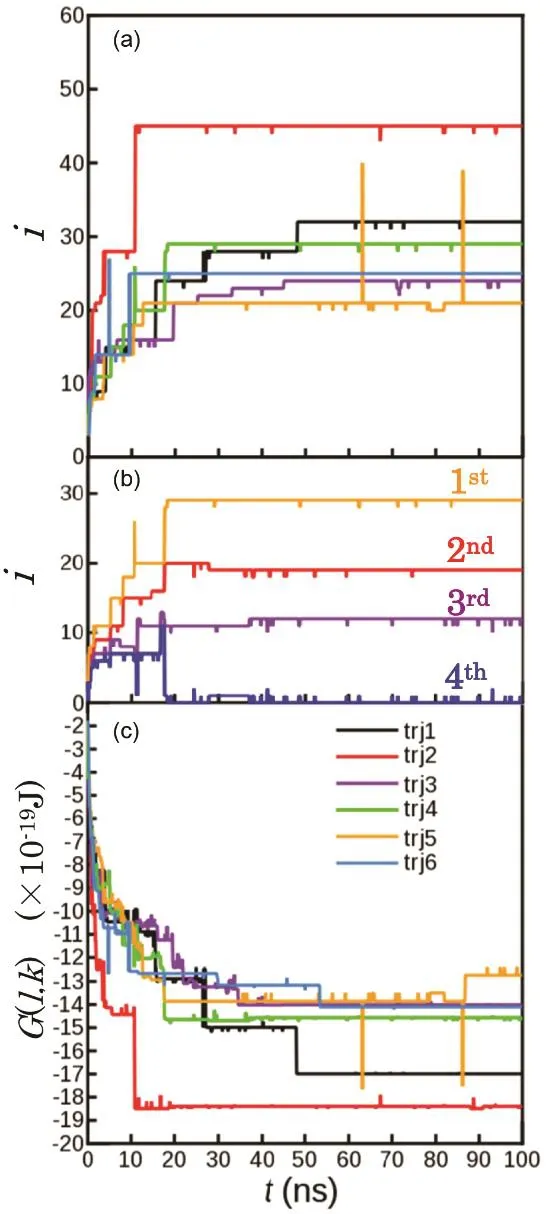
Fig. 7 Time evolution of (a) maximum aggregation number, i, of aggregates in the independent six aggregation simulations, (b) four largest aggregation numbers for one trajectory, green line in Fig. 7a,and (c) free energy profile G(l, t) of the system evaluated by Eq. (14) for each trajectory.Results of the six independent MD runs are plotted in different colors in (a) and (c).

This indicated that the results do not strongly depend on the details of potential parameters. In contrast, as described in the introduction, the time evolution of the maximum aggregation number greatly differs depending on whether the hydrophilic group is ionic, zwitterionic or nonionic24. The electric charge of the hydrophilic group has a strong influence on the rate of aggregation.

The time evolution of the free energy G(l, t) was evaluated by Eq. (14) for each trajectory. For all l, G(l, t) decreases with increasing time. As described in Section 3.3, it is thermodynamically stable to form one aggregate. However, the aggregation was not actually completed during the 100-ns-long simulation, and the system did not reach the equilibrium state.A kinetic mechanism is considered to prevent the fragment from aggregating each other.

3.5 Aggregation kinetics

The kinetics concerned with the aggregation between the aggregates is dominated by two factors: (1) collision by diffusion, and (2) crossing the free energy barrier along the reaction coordinates of the aggregation.

Here, the frequency of collision between the aggregates caused by diffusion is evaluated to examine whether the 100 ns long simulation was sufficient for the aggregates to diffuse and collide each other. For this purpose, we use the fast passage time, which is often used to evaluate the reaction time in a diffusion-controlled reaction where the reaction proceeds by the contact of two spherical particles in solution26. First, one aggregate is fixed in space. The range of motion of another aggregate is assumed to be inside a sphere of radius R centered on the fixed aggregate, and the area outside the sphere with radius Rm (＜ R), which is the sum of the radii of two aggregates that are fixed and diffusible. Then, the fast passage time, tFPT, is given by,

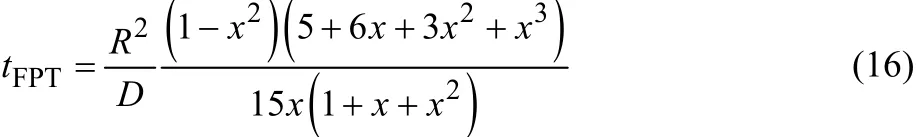
where x = Rm/R. D is the diffusion coefficient of the two aggregates, and the sum of the self-diffusion coefficients of the individual aggregates is commonly used. The self-diffusion coefficient of the individual aggregate was evaluated from the Einstein-Stokes law (D = kBT/6πηRm), where the viscosity coefficient, η, of water at 300 K is 0.000853 Pa·s32, and Rm is obtained from the radius of gyration by the MD calculation(1.34 nm at N = 3133).

The time required for the contact between two aggregates (N =31) in the aggregation simulation is estimated to be 20 ns from tFPT. Therefore, several collisions should have occurred in the last 50–70 ns. However, the aggregation did not occur for all independent six simulations. Thus, the aggregation is not a diffusion-controlled process.

A repulsive interaction coming from free energy barrier must exist between aggregates. The repulsive force may be produced by the overlap of the electric double layer formed on the surface of the aggregates by the negative charge of the surfactant molecules and the positive charge of the counter ions. More than 100 ns are necessary to pass the free energy barrier by to form the stable micelles.

4 Conclusions

In this study, the free energy landscape,of aggregation was investigated using the free energy,, of micelle formation obtained by MD calculations. This analysis is based on chemical species model. The calculatedwas negative for all aggregations where the sum of the number of DS ions in the two aggregates was 60 or less. From the viewpoint of chemical equilibrium, aggregation to the stable micelle is desired.

Further, free energy profile along possible aggregation pathways was investigated from small aggregates to thermodynamically stable complete micelles in solution. The free energy profile G(l, k) of the aggregates was evaluated by. All aggregation pathways were obtained from the initial state of 12 pentamers to the stable micelle with i = 60. The calculated G(l, k) all monotonically decreases with increasing k. The absolute valuewas an order of magnitude greater than that, dominating the aggregation process.

Independent six MD calculations were performed for the spontaneous aggregation process of SDS dispersed in water. In each calculation, 10–30-mers were formed within about 20 ns.However, the aggregation did not proceed more and was not completed even after 100 ns simulations, despite the fact that the SDS micelle with i ≈ 60 is the most thermodynamically stable. For each run, the free energy decreased sharply with time for the first 20 ns, but hardly changed after that.

The time required for a collision between aggregates was evaluated using the fast passage time, tFPT. The calculated tFPTwas about 20 ns for the aggregates with N = 31. Thus, if aggregation is a diffusion-controlled process, the aggregation should be completed within the 100 ns simulation. However, in fact, the aggregation does not proceed. This is due to the free energy barrier between the aggregates, that is, the repulsive force acting on them. This may be caused by electrostatic repulsion produced by the overlap of the electric double layers formed by the negative charge of the hydrophilic groups and counter sodium ions on the surface of the aggregates. In order to aggregate to form stable micelles the aggregates are required to pass this barrier thermally.

The potential of mean force between aggregates must be evaluated to obtain the time constant for the aggregation of two aggregates to form the stable micelle34. We discuss this free energy barrier elsewhere35, based on free energy calculation combined with molecular dynamics calculation.

Acknowledgment: Calculations were mainly performed at the Research Center for Computational Science, Okazaki,Japan, partially at the Information Technology Center of Nagoya University, and partially at the Institute for Solid State Physics, the University of Tokyo.

Supporting Information: available free of charge via the internet at http://www.whxb.pku.edu.cn.

References and Notes

(1) Tanford, C. J. Phys. Chem. 1974, 78, 2469.doi: 10.1021/j100617a012

(2) Israelachvili, J. N. Intermolecular and Surface Forces, 2nd ed.;Academic Press: London, UK, 1992.

(3) Everett, D. H. Basic Principles of Colloid Science; The Royal Society of Chemistry: London, UK, 1988.

(4) Puvvada, S.; Blankschtein, D. J. Chem. Phys. 1990, 92, 3710.doi: 10.1063/1.457829

(5) Christopher, P. S.; Oxtoby, D. W. J. Chem. Phys. 2003, 118, 5665.doi: 10.1063/1.1554394

(6) Maibaum, L.; Dinner, A. R.; Chandler, D. J. Phys. Chem. B 2004,108, 6778. doi: 10.1021/jp037487t

(7) Yoshii, N.; Iwahashi, K.; Okazaki, S. J. Chem. Phys. 2006, 124,184901. doi: 10.1063/1.2179074

(8) Pool, R.; Bolhuis, P. G. J. Chem. Phys. 2007, 126, 244703.doi: 10.1063/1.2741513

(9) Burov, S. V.; Shchekin, A. K. J. Chem. Phys. 2010, 133, 244109.doi: 10.1063/1.3519815

(10) Verde, A. V.; Frenkel, D. Soft Matter 2010, 6, 3815.doi: 10.1039/C0SM00011F

(11) Bernardino, K.; de Moura, A. F. J. Phys. Chem. B 2013, 117, 7324.doi: 10.1021/jp312840y

(12) Marrink, S. J.; Tieleman, D. P.; Mark, A. E. J. Phys. Chem. B 2000,104, 12165. doi: 10.1021/jp001898h

(13) Lazaridis, T.; Mallik, B.; Chen, Y. J. Phys. Chem. B 2005, 109,15098. doi: 10.1021/jp0516801

(14) Tieleman, D. P.; van der Spoel, D.; Berendsen, H. J. C. J. Phys.Chem. B 2000, 104, 6380. doi: 10.1021/jp001268f

(15) Bond, P. J.; Cuthbertson, J. M.; Deol, S. S.; Sansom, M. S. P. J. Am.Chem. Soc. 2004, 126, 15948. doi: 10.1021/ja044819e

(16) Jusufi, A.; Hynninen, A. -P.; Panagiotopoulos, A. Z. J. Phys. Chem. B 2008, 112, 13783. doi: 10.1021/jp8043225

(17) Sanders, S.; Sammalkorpi, M.; Panagiotopoulos, A. Z. J. Phys. Chem.B 2012, 116, 2430. doi: 10.1021/jp209207p

(18) Sammalkorpi, M.; Karttunen, M.; Haataja, M. J. Phys. Chem. B 2007,111, 11722. doi: 10.1021/jp072587a

(19) Cheong, D.; Panagiotopoulos, A. Z. Langmuir 2006, 22, 4076.doi: 10.1021/la053511d

(20) Pool, R.; Bolhuis, P. G. J. Phys. Chem. B 2005, 109, 6650.doi: 10.1021/jp045576f

(21) Pool, R.; Bolhuis, P. G. Phys. Rev. Lett. 2006, 97, 018302.doi: 10.1103/PhysRevLett.97.018302

(22) Pool, R.; Bolhuis, P. G. Phys. Chem. Chem. Phys. 2006, 8, 941.doi: 10.1039/B512960E

(23) Kawada, S.; Komori, M.; Fujimoto, K.; Yoshii, N.; Okazaki, S. Chem.Phys. Lett. 2016, 646, 36. doi: 10.1016/j.cplett.2015.12.062

(24) Fujimoto, K.; Kubo, Y.; Kawada, S.; Yoshii, N.; Okazaki, S. Mol.Simul. 2017, 43, 13. doi: 10.1080/08927022.2017.1328557

(25) Lifshitz, I. M.; Slyozov, V. V. J. Phys. Chem. Solids 1961, 19, 35.doi: 10.1016/0022-3697(61)90054-3

(26) Szabo, A.; Schulten, K.; Schulten, Z. J. Chem. Phys. 1980, 72, 4350.doi: 10.1063/1.439715

(27) Moore, W. J. Physical Chemistry, 4th ed.; Prentice Hall, Inc.: Upper Saddle River, NJ, USA, 1972.

(28) Everett, D. H. Colloids Surf. 1986, 21, 41.doi: 10.1016/0166-6622(86)80081-6

(29) Yoshii, N.; Okazaki, S. Chem. Phys. Lett. 2006, 425, 58.doi: 10.1016/j.cplett.2006.05.004

(30) Yoshii, N.; Okazaki, S. Chem. Phys. Lett. 2006, 426, 66.doi: 10.1016/j.cplett.2006.05.038

(31) Aniansson, E. A. G.; Wall, S. N. J. Phys. Chem. 1974, 78, 1024.doi: 10.1021/j100603a016

(32) Kestin, J.; Sokolov, M.; Wakeham, W. A. J. Phys. Chem. Ref. Data 1978, 7, 941. doi: 10.1063/1.555581

(33) The value obtained in Eq. (1) of Ref. 28 was used.

(34) Russel, W. B.; Saville, D. A.; Schowalter, W. R. Colloidal Dispersions; Cambridge University Press: Cambridge, UK, 1989.

(35) Kawada, S.; Fujimoto, K.; Yoshii, N.; Okazaki, S. J. Chem.Phys. 2017, 147, 084903. doi: 10.1063/1.4998549