Deformation of Polymer-Grafted Janus Nanosheet: A Dissipative Particle Dynamic Simulations Study

LU Teng , ZHOU Yongxiang ,2, GUO Hongxia ,2,＊

1 Beijing National Laboratory for Molecular Sciences, Joint Laboratory of Polymer Sciences and Materials, State Key Laboratory of Polymer Physics and Chemistry, Institute of Chemistry, Chinese Academy of Sciences, Beijing 100190, P. R. China.

2 University of Chinese Academy of Sciences, Beijing 100049, P. R. China.

Abstract: Because of broad potential applications in sensing,drug delivery, and molecular motors, two-dimensional (2D),flexible, responsive Janus materials have attracted considerable interest recently in many fields. Unfortunately, the molecular-level responsive deformation of these 2D Janus nanomaterials is still not clearly understood. Hence, investigating the influence factor and responsiveness of the deformation of the 2D flexible responsive Janus nanomaterials should be helpful to deepen our understanding of the deformation mechanism and may provide valuable information in the design and synthesis of novel functional 2D Janus nanomaterials. Therefore, a mesoscopic simulation method, dissipative particle dynamics simulation,based on coarse-grained models, is employed in this work to systematically investigate the effect of the chain length difference between grafted polymers within two compartments of each individual Janus nanosheet and the effect of solvent selectivity difference of these two compartments on the deformation of the polymer-grafted Janus nanosheet.Although the coarse-grained model within this simulation is relatively crude, it is still valid to provide a qualitative image of the deformation of the polymer-grafted Janus nanosheet. Furthermore, we find two basic principles: (1) with increasing length difference between grafted polymers on the two opposite surfaces, the nanosheet will bear an entropy-driven deformation with increasing curvature; (2) the solvent will preferentially wet the polymer layer with better compatibility, and such a swelling effect may also provide a driving force for the deformation process. Owing to the interplay of conformational entropy and mixing enthalpy, the equilibrium structures of the polymer-grafted Janus nanosheet result in several interesting structures, such as a tube-like structure with a hydrophobic outer surface, an envelope-like structure,and a bowl-like structure, with tuning of the chain length and solvent compatibility of grafted polymers. Additionally, an unusually tube-like structure with a hydrophobic outer surface has been observed for a relatively weak solvent selectivity,which may provide us a novel method to transfer materials into the incompatible environment and therefore has potential applications in many areas, such as controllable drug delivery and release, and industrial and medical detection. Our theoretical results first provide a fundamental insight into the controllable deformation of the flexible Janus nanosheet,which can then help in the design and synthesis of novel Janus nanodevices for potential applications in pharmaceuticals and biomedicine. Bearing the limited of the computational capabilities, our model Janus nanosheets are relatively small,which are not direct mappings from real system. We hope that a systematic simulation study on this topic would be possible soon with the rapid developments in computer technology and simulation methods, and this would provide an exhaustive and universal methodology to guide experimental studies and applications.

Key Words: Janus nanomaterial; Polymer; Amphiphilic composites; Morphology control; Dissipative particle dynamics simulation

1 Introduction

After introduced by de Gennes in his Nobel Prize address,Janus materials which typically contain two compartments of different chemical makeups or surface properties within the same particle have attracted much attention due to their fundamental and applied interest1–7. Since then, several theoretical and experimental studies show that Janus nanoparticles can behave like surfactant particles that strongly adsorb and orient at the liquid-liquid interface and pronouncedly reduce the interfacial tension8,9, which makes Janus nanoparticles as a novel type of efficient compatibilizer for polymer blends10–13. Moreover, recent works have illustrated that beyond the size and coating of Janus nanoparticles, the particle shape is another principal factor affecting the interfacial properties of polymer blends14–19as well as their motion behavior20. Therefore, Janus nanoparticles have experienced fast development in their synthesis methodology and Janus nanoparticles with varied compositions or architectures can be generated21.

Among various shapes, 2D (platelet, sheet or disc) Janus nanoparticles have gained lots of attention as a special type of solid surfactant. For example, the emulsions could be stabilized much more by mosaicking the Janus platelets onto the interface22.Consequently, considerable attentions have been paid to the synthesis methodology of Janus sheets/disks/platelets,especially responsive flexible ones. Recently, nanometer sized polymeric Janus disks have been synthesized by cross-linking those supramolecular structures from block copolymers23–26and polymeric/inorganic composite Janus nanosheets are derived by a favorable growth of polymer chains onto one side of the nanosheets27–30. Particularly, several works have reported on fabricating flexible responsive Janus nanosheets.Liu et al. proposed a facile approach for generating Janus silica nanosheets through both surface sol-gel process onto a template and surface modification, which can wrap desired species upon pH change31. Meanwhile, Qi et al. prepared a uniform poly(acrylic acid)-b-poly(ε-caprolactone)-b-poly(acrylic acid)sandwiched single crystals by poly(ε-caprolactone)-b-poly(acrylic acid) and then generated pH-responsive polymeric Janus nanosheets after a selective cross-linking of poly(acrylic acid)32.More recently, a flexible and thermal responsive polymeric Janus nanosheet has been synthesized by a general polymerization method of sequential addition-fragmentation chain transfer grafting from a template particle surface, which are tunable by feeding sequence and type of monomers and can form a scrolled superstructure33. In a word, the 2D Janus nanomaterials, especially flexible responsive ones show fascinating features and novel application potentiality due to their highly anisotropic shapes and unique deformability.However, due to the existence of substrates during the synthesis, the molecular-level understanding of the responsive deformation of these 2D Janus nanomaterials is still lacking.Therefore, it is well worth investigate the properties of freestanding Janus nanosheet and explore its potential applications in various fields.

With the rapid increase in computational power, molecular simulations have become a potential method to address the limitations of both analytical and experimental approaches.Especially, a relatively new mesoscopic simulation technique,dissipative particle dynamic (DPD) simulation that can model much larger system sizes with much longer time scales than atomistic molecular dynamics simulations has been applied to the study of the nanoparticle/polymer composites9,34–37. This is because in DPD simulations each bead represents a cluster of atoms or molecules and interacts each other via soft conservative potentials. Taking advantage of reduced number of interaction sites and the timescale speed-up, DPD is well suited for studying the large-scale cooperative behavior, like self-assembly or phase transitions38–41. Given these, we adopt the DPD simulation technique and systematically study the deformation behavior of the flexible Janus nanosheets.

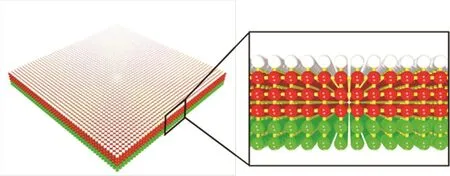
Fig. 1 Schematic of the model of polymer grafted Janus sheet.The nanosheet is constructed by three layers of cross-linking particles while the opposite surfaces are grafted different polymer chains.The white, red and green particles represent polymer A, nanosheet and polymer B, respectively. color online.

2 Simulation model and methods

Our simulation system contains water and polymer grafted Janus sheets. As we known, a fascinating feature of the 2D Janus particle is its highly anisotropic shape, according to ref.15, the typical Janus nanosheet (～4 μm) is only 5.5-nm-thick.Unfortunately, the aspect ratio of the Janus nanosheet is too high to be mapping directly. However, we try to introduce a simple model just to provide a qualitative image of the deformation of the polymer-grafted Janus nanosheet. Hence,the simplified model of Janus nanosheet must be computationally affordable Based on these considerations, the CG model of nanosheet is constructed by three layers of DPD particles, each layer is consisting of 50 × 50 DPD particles while each particle cross-links to its nearest neighbors which is illustrated in Fig. 1. Our nanosheet model is constructed in four steps: in the initial condition, the nanosheet particles are placed to lattice points in a regular array (shown as red particles in Fig.1); afterwards, each particle will be bonded to its six nearest neighbors; then, the model polymer A and B with different feature and length the particles are grafted to the opposite surfaces, respectively; finally, the model will be relaxed to the equilibrium state. As we mentioned above, the aspect ratio of our model nanosheet is much smaller than the realistic one which should make the deformation much more difficult.Hence, bending forces are not considered advisedly for reducing the bending modulus. Note our models are relatively crude, which are not direct mappings from real system.However, we find that this simple model can still qualitatively provide the image of the deformation of the polymer-grafted Janus nanosheet. Moreover, the bonded interaction is described as a harmonic spring force of= k(rij– r0)eijbetween the adjacent particles, where the spring constant and the equilibrium bond length are set to k = 100 and r0= 0.7rc,respectively. To our knowledge, the length of the grafted polymer should be a vital factor on the deformation behavior of the flexible Janus nanosheets, we fix the length of the grafted polymer A at Np1= 1 and change the length of polymer B Np2from 1 to 6 to systematically investigate the effect of the length difference. Moreover, the solvent selectivity should be another vital factor. In our system, there are four types of particles(water w, nanosheet n and polymer A/B p1/p2) which makes the interaction parameter space of our study rather large. For simplification, we set all the repulsive parameters for the kindred particles to the usual value of aww= ann= ap1p1= ap2p2=25 while for the unlike particles, they are all set as 75 except the interaction parameters between water and grafted polymers.We hence are only concerned with the affinities of grafted polymers with solvent (water) and tailor such an affinity effect by symmetrically tuning the awp1and awp2.As a result, the awp2−awp1varies from −45 to 45. The complete list of repulsion interaction parameters for our simulation systems are given in Table 1. More details of the DPD simulation can be found in our previous works3.

The cutoff radius rc, the bead mass m0, and the temperature kBT are taken as length, mass, and energy unities, respectively.Then the reduced time unit is defined as τ = (m0r2c/kBT)−1/2. The equations of motion are integrated using a modified velocity-Verlet algorithm at λ = 0.65 with a time step of Δt =0.05τ. All simulations are performed in the NVT ensemble at constant temperature kBT = 1 and constant density ρ0= 3 while periodic boundary conditions are applied in all three dimensions. Since the interaction between Janus nanosheets is out of consideration, our simulation system only consists of a single Janus nanosheet. At the beginning, the Janus sheet is located at the center of the simulation box of size and the box isfilled with water particles randomly (the water particles are included explicitly in the simulations, but not shown in figures for clarity) while the total particles are of 375000. In the present work, every simulation begins with an equilibrating progress of 500τ under athermal condition (i.e., all repulsion interaction parameters are set at 25). Then, the repulsion interaction parameters are reset to the desired values and the simulation will be performed until the equilibration is considered to be reached (i.e., the total energy and pressure of the system do not change within the simulation time).Additionally, to ensure the resulting structure is a good representation of those studied samples, we repeat the above simulation processes independently at least four times from different initial configurations. We choose the structures with lowest total energy as the equilibrating structure for the different final structures.

Table 1 Repulsion parameters used in the simulation.

3 Results and discussion

The typical equilibrating structures observed in our simulation are shown in Fig. 2. It’s worth noting that many fascinating structures reported recently (such as nanobowl32,nanoscroll33,42and so on) have been reproduced in our simulations, which we will discuss in the following section. As mention above, our primary focus is to systematically investigate the effect of the length difference and solvent selectivity on the deformation behavior of the polymer grafted Janus nanosheets. Accordingly, we fix the length of polymer A at Np1 = 1 and vary the Np2 from 1 to 6 to survey the effect of length difference between the grafted polymers. On the other hand, we keep awp1− 25 = 25 − awp2and vary the difference between them awp2− awp1from −45 to 45 for solvent selectivity study. Finally, the phase diagram of equilibrating structures as a function of the Np2− Np1and awp2− awp1can be provided for an entire and distinct description of the results in Fig. 3.

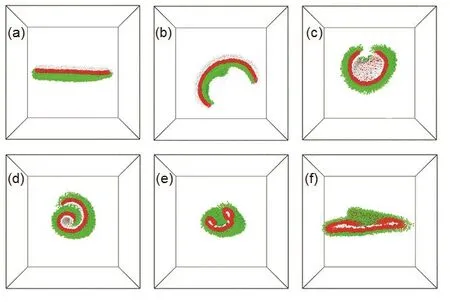
Fig. 2 Schematic of typical equilibrating structures: (a) plate;(b) inverse-bowl; (c) nanotube; (d) scroll; (e) double-scroll; (f) envelope.For better visibility, the nanosheets are shown as sectional while the water particles are omitted.

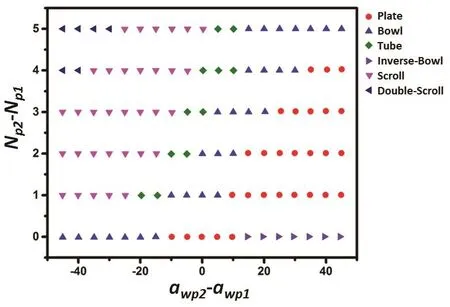
Fig. 3 Phase diagram of equilibrating structures as a function of the Np2 − Np1 and awp2 − awp1.

At first, we focus on two lines within this phase diagram:one is under the neutral condition, i.e., the compatibilities of the two kinds of polymer with the solvent are equivalent;another one is with the equilong grafted polymers. Under the former condition, the deformation is mainly governed by the conformational entropy, since the mixing enthalpy at the two surfaces are approximate. Obviously, when the grafted polymers at the opposite surfaces are equilong, the nanosheet keeps as strait plate (shown in Fig. 4a). However, the deformation appears for a little length difference, resulting in a bending bowl-like structure. Moreover, with the increasing of the polymer length, the nanosheet becomes more and more bent and form the tube-like structure, until falling in the scroll-like structure finally. For the latter condition, the deformation is certainly depending on the contribution of mixing enthalpy.And as shown in Fig. 5a–e, a distinct dewetting process can be observed. When the compatibility of polymer B with solvent is relatively good, there are many water particles locating at the polymer B layer which surely expand the grafted layer and cause a large curvature (shown in Fig. 5a). However, with the increasing of awp2, water particles are gradually excluded from the grafted layer, resulting in the decreasing of the curvature.At last, when the compatibilities of both polymers with solvent are equal, the nanosheet will finally restore the equilibrating structure of plate under the neutral condition (Shown in Fig.5e). Otherwise, as shown in Fig. 5e–i, when the awp2 keep increasing (meanwhile, the awp1 will decrease synchronously),the deformation will arise again, but to the inverse side. To sum up, there lie two basic principles: with the increasing of length difference between grafted polymers on the two opposite surfaces, the nanosheet will bear an entropy-driven deformation with increasing curvature; the solvent will preferentially wet the polymer layer with better compatibility, and such swelling effect may also provide a driving force of the deformation process.

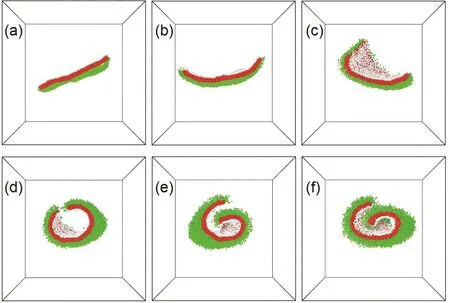
Fig. 4 Equilibrating structures for awp2 = awp1 with varied grafted length difference: (a) 1 : 1, (b) 1 : 2, (c) 1 : 3, (d) 1 : 4, (e) 1 : 5,(f) 1 : 6, respectively.For better visibility, the nanosheets are shown as sectional viewwhile the water particles are omitted.

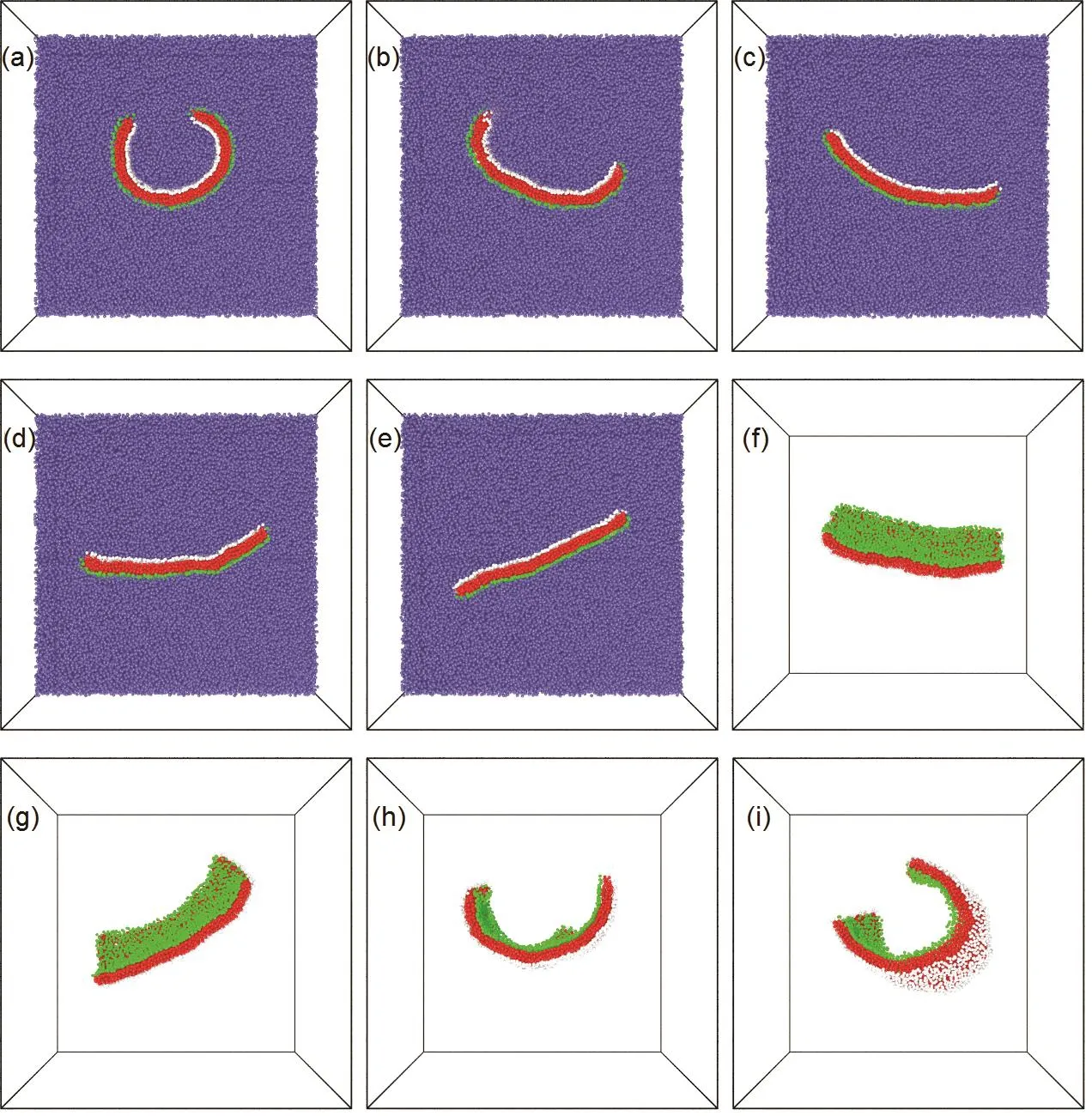
Fig. 5 Equilibrating structures at fixed grafted length 1 : 1 with varied solvent selectivity awp2 − awp1 = (a) −40, (b) -30, (c) −20, (d) −10,(e) 0, (f) 10, (g) 20, (h) 30, (i) 40, respectively.For better visibility, the nanosheets are shown as sectional viewwhile the water particles are omitted in (f)–(i).

Following the diagonal from the left upper corner to the right lower part, the phase diagram can be separated into six regions corresponding to different structures. At the left upper corner of the phase diagram, the grafted polymer B is quite hydrophilic and relatively long. As mentioned above, the longer grafted polymers prefer to become more disorder to earn larger profit of the conformational entropy, which can also provide more wettable space in the polymer layer. This win-win situation will certainly drive the nanosheet to expand the grafted surface mostly for both the conformational entropy and mixing enthalpy favor. Consequently, the nanosheet will deform into a double-scroll structure to gain a large curve and expose the polymer B grafted surface mostly to the water. With a bit decreasing of both length difference and solvent selectivity, the trend of bending is decreasing simultaneously, resulting in the scroll structure with smaller curvature. Obviously, this structure lies a large area in the phase diagram which suggestion the scroll structure should be quite stable. However, unlike in the double-scroll region, the deformation cannot gain the contribution from both the conformational entropy and mixing enthalpy at the same time, but still follow the principles we mentioned above: for the same grafted length, the nanosheet with a larger solvent selectivity shows the larger curvature as well as the longer grafted nanosheet with the equal solvent selectivity. Consequently, the largest curvature will be present at the suitable balance between the length difference and the solvent selectivity (the data isn’t shown here). Next, nearly to the neutral region, where the compatibility between the two kinds of polymer and the solvent are relatively approximate,the deformation shows less bending and performs as a tube-like structure. Interestingly, an unusual phenomenon appears in this region. For considerable grafted length difference, we find the nanosheet may deform into a tube-like structure leaving the hydrophobic surface outside while the solvent selectivity is not too strong. This unusual coverture may provide us a novel method to transfer materials into the incompatible environment and therefore has potential application in many areas, such as controllable drug delivery and release, industrial and medical detection and so on. In the next region, the longer grafted polymer is incompatible to the solvent. Under this situation, the grafted polymers are forced to packing inseparably which could reduce the immiscible interface but also suffer the loss of the conformational entropy. The last region is at the right lower corner, for the symmetrical grafted polymers of worse compatibility, the nanosheet will show a distinct departure from plate structure to form a series of bending structures (shown in Fig. 5g–i) which we define as inverse-bowl structure since, the bending is arising to the reverse side. Additionally, we construct a larger Janus nanosheet which is fourfold the size of the small one. After a quite long-time equilibrium process, we finally observe a new envelope-like structure (shown in Fig. 2f)which forms at considerably strong solvent selectivity with relatively short grafted polymers. In this state, the nanosheet fold into bilayer or schistic micelle like structure and all the solvent are excluded from its inside. Unfortunately, this system is too large and too computationally costly which make the systematically study unaffordable at present. With the rapid development in computer technology and simulation method,we hope the systematically simulation study on this realm could be possible soon and may provide an exhaustive and universal conclusion to guide the experimental studies and applications.

4 Conclusions

In this study, by DPD simulations, we study the deformation behavior of the polymer-grafted Janus nanosheets. The effects of the length difference between grafted polymers and solvent selectivity of the grafted polymers have been systematically studied. Generally speaking, with the length difference between grafted polymers increasing, the Janus nanosheet become more bending because the contribution of the conformational entropy. In addition, when the lengths of the grafted polymers are equivalent, the deformation will be governed by the mixing enthalpy which depends on the solvent selectivity. Therefore,the equilibrating structures are driven by the synergistic reaction of the conformational entropy as well as the mixing enthalpy. Moreover, not only the fascinating structures reported by recently research are observed, but also the undiscovered ones have been predicted.Our studies may provide a fundamental understanding of the controllable deformation of the flexile Janus nanosheet, which we hope can provide useful guiding to design novel Janus nanodevices and extend further application of 2D Janus materials.

Acknowledgment: The authors gratefully acknowledge the National Supercomputer Centre in Guangzhou and the Supercomputer Center of Chinese Academy of Sciencesfor their computing resource support.