Hessian Comparison and Spectrum Lower Bound of Almost Hermitian Manifolds∗

Chengjie YU

Abstract The authors obtain a complex Hessian comparison for almost Hermitian manifolds,which generalizes the Laplacian comparison for almost Hermitian manifolds by Tossati,and a sharp spectrum lower bound for compact quasi Kähler manifolds and a sharp complex Hessian comparison on nearly Kähler manifolds that generalize previous results of Aubin,Li Wang and Tam-Yu.

Keywords Almost-Hermitian manifolds,Quasi Kähler manifolds,Nearly Kähler manifolds

1 Introduction

A triple(M,J,g)is called an almost Hermitian manifold if J is an almost complex structure and g is a J-invariant Riemannian metric.There are two connections,one is the Levi-Civita connection and the other one is the canonical connection,on almost Hermitian manifolds,that play important roles on the geometry of almost Hermitian manifolds.The canonical connection is an extension of the Chern connection[6]on Hermitian manifolds.It was first introduced by Ehresmann-Libermann[9].

Geometers were used to use the Levi-Civita connection for the study of the geometry of almost Hermitian manifolds,see for example[1,13–16].However,later researches show that canonical connection is useful for the study of the geometry of almost Hermitian manifolds.For example,canonical connection is crucial for the study of the structure of nearly Kähler manifolds in[3,24–25].In[30],Tossati,Weinkove and Yau used the canonical connection to solve the Calabi-Yau equation on almost Kähler manifolds.The problem that Tossati,Weinkove and Yau considered is part of a program proposed by Donaldson[7–8]on sympletic topology.In[29],Tossati obtained a Laplacian comparison result about the canonical connection on almost Hermitian manifolds using the second variation of arc length and obtained a Schwartz lemma on almost Hermitian manifolds which is a generalization of the Schwartz lemma by Yau[31].

In this paper,by applying the same Bochner technique as in[22],we obtain a Hessian comparison on almost Hermitian manifolds which generalises Tossati’s Laplacian comparison(see[29]).More precisely,we obtain the following result.

Theorem 1.1 Let(M,J,g)be a complete almost Hermitian manifold with holomorphic bisectional curvature bounded from below by−K with K ≥0,torsion bounded by A1and the(2,0)part of the curvature tensor bounded by A2.Let o be a fixed point in M and ρ be the distance function to o.Then

within the cut-locus of o whereHere ρijmeans the complex Hessian of ρ with respect to the canonical connection.

Moreover,with the same technique,we obtain the following sharp diameter estimate for almost Hermitian manifolds.

Theorem 1.2 Let(M,J,g)be a complete almost Hermitian manifold with quasi holomorphic sectional curvature not less than K>0.Then

For the definition of quasi holomorphic sectional curvature,see Definition 3.2.It extends the notion with the same name for Hermitian manifolds in[4]to almost Hermitian manifolds.In fact,the above diameter estimate was disguised with a seemingly different curvature assumption in[14].However,one can show that the two curvature assumptions are the same by using the curvature identities derived in[32].The same diameter estimate for Hermitian manifolds was also obtained in[4].

Our method to prove Theorem 1.1 and Theorem 1.2 is different from those in[4,14,29]where the authors all used the second variation of arc length.Our method here is first to compute the evolution ordinary differential equation of the Hessian of ρ along a normal geodesic which turns out to be a matrix Riccati equation.Then the comparison theorems for matrix Riccati of Royden[27]gives us the conclusions directly.The technique was used in[22].

Furthermore,by using a similar technique as in[2,11],we have the following sharp spectrum lower bound for compact quasi Kähler manifolds.

Theorem 1.3 Let(M,J,g)be a compact quasi Kähler manifold with the quasi Ricci curvature bounded from below by a positive constant K.Then λ1≥ 2K,where λ1is the first eigenvalue for the Laplacian operator of(M,g).

For the definition of quasi Ricci curvature,see Definition 4.1.In fact,this result generalizes the corresponding result of Aubin[2]on compact Kähler manifolds to compact quasi Kähler manifolds.Moreover,note that the equality in the result is not only achieved by CPnwith Fubini-Study metric but also be achieved by non-Kähler manifolds.For example,the six dimensional sphere with the standard complex structure and standard metric.Moreover,one should note that the quasi Kähler structure is crucial for the sharp spectrum lower bound above.By a classical result of Lichnerowicz[23],the specturm lower bound for n dimensional compact Riemannian manifolds with Ricci curvature not less than(n−1)K is nK.It was shown by Obata[26]that the equality holds if and only if the manifold is a round sphere.The sharp spectrum lower bound of Lichnerowicz is not sharp for quasi Kähler manifolds.

Finally,we obtain a sharp Hessian comparison on nearly Kähler manifolds which generalizes some results in[22,28]on Kähler manifolds.

Theorem 1.4 Let(M,J,g)be a complete nearly Kähler manifold and o be a fixed point in M.Let Bo(R)be a geodesic ball within the cut-locus of o.Suppose that the quasi holomorphic bisectional curvature on Bo(R)is not less than K,where K is a constant.Then

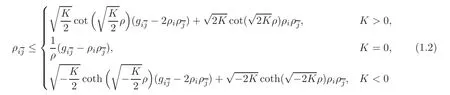
in Bo(R)with equality holds all over Bo(R)if and only if Bo(R)is holomorphic and isometric equivalent to the geodesic ball with radius R in the Kähler space form of constant holomorphic bisectional curvature K,where ρ is the distance function to the fixed point o.

For the definition of quasi holomorphic bisectional curvature,see Definition 5.1.By the application of the Hessian comparison above,we can obtain eigenvalue comparison and volume comparison on nearly Kähler manifolds by classical arguments.Please see Section 5 for details.

Note that in[30],Tossati,Weinkove and Yau introduced a new notion of curvature that couples up the(1,1)-part of the curvature tensor and the torsion of the canonical connection on almost Kähler manifolds and is crucial for solving the Calabi-Yau equation on almost Kähler manifolds.In this paper,the new notions of curvature defined are different with that of Tossati,Weinkove and Yau.We hope that the new notions of curvature introduced here for almost Hermitian manifolds,quasi Kähler manifolds and nearly Kähler manifolds have some further applications.

The outline of the paper is as follows.In Section 2,we recall some preliminaries in almost Hermitian geometry and generalized Kähler geometry.In Section 3,we prove Theorem 1.1 and Theorem 1.2.In Section 4,we prove Theorem 1.3.Finally,in Section 5,we prove Thereom 1.4 and present some of its corollaries.

2 Preliminaries

In this section,we recall some definitions and known results for almost Hermitian manifolds,quasi Kähler manifolds and nearly Kähler manifolds.

Definition 2.1(see[12,19–20]) Let(M,J)be an almost complex manifold.A Riemannian metric g on M such that g(JX,JY)=g(X,Y)for any two tangent vectors X and Y is called an almost Hermitian metric.The triple(M,J,g)is called an almost Hermitian manifold.The two form ωg=g(JX,Y)is called the fundamental form of the almost Hermitian manifold.A connection∇ on an almost Hermitian manifold(M,J,g)such that∇g=0 and∇J=0 is called an almost Hermitian connection.

Note that the torsion τ of the connection ∇ is a vector-valued two form defined as

An almost Hermitian connection is uniquely determined by its(1,1)-part.In particular,there is a unique almost Hermitian connection with vanishing(1,1)-part.Such a connection is called the canonical connection which was first introduced by Ehresman and Libermann[9].

Definition 2.2(see[19–20])The unique almost Hermitian connection ∇ on an almost Hermitian manifold(M,J,g)with vanishing(1,1)-part of the torsion is called the canonical connection of the almost Hermitian manifold.

For sake of convenience,we adopt the following conventions in the remaining part of this paper:

(1)Without further indications,the manifold is of real dimension 2n.

(2)D denotes the Levi-Civita connection and RLdenotes its curvature tensor and “,” means taking covariant derivatives with respect to D.

(3)∇ denotes the canonical connection,R denotes the curvature tensor of∇ and “;”means taking covariant derivatives with respect to∇.

(4)Without further indications,a,b,c,d denote indices in{1,1,···,n,n}.

(5)Without further indications,i,j,k,l denote indices in{1,2,···,n}.

(6)Without further indications, α,β,λ,µ,ν denote summation indices going through{1,2,···,n}.

Recall the definition of curvature operator:

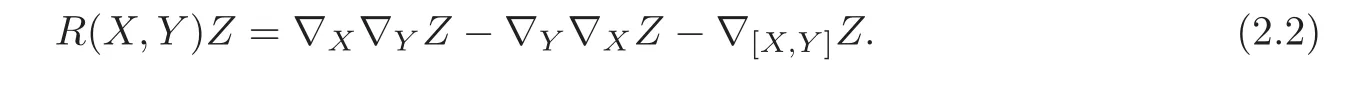
The curvature tensor is defined as

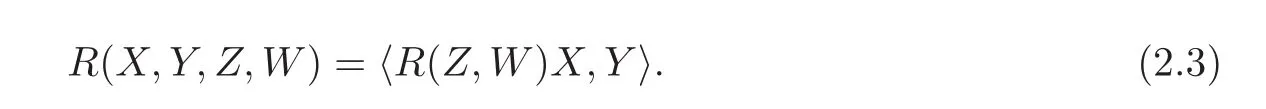
Fixed a unitary(1,0)-frame(e1,e2,···,en),since ∇J=0,we have

for all indices i,j and a,b.Moreover,similarly as in the Riemannian case,we have the following symmetries of the curvature tensor:

for all indices a,b,c and d.Recall thatare called the first and the second Ricci curvature of the almost Hermitian metric g respectively.

The following first Bianchi identities for almost Hermitian manifolds are frequently used in the computations of the remaining part of this paper.One can find them in[19,30,32].

Proposition 2.1 Let(M,J,g)be an almost Hermitian manifold.Fixed a unitary frame,we have

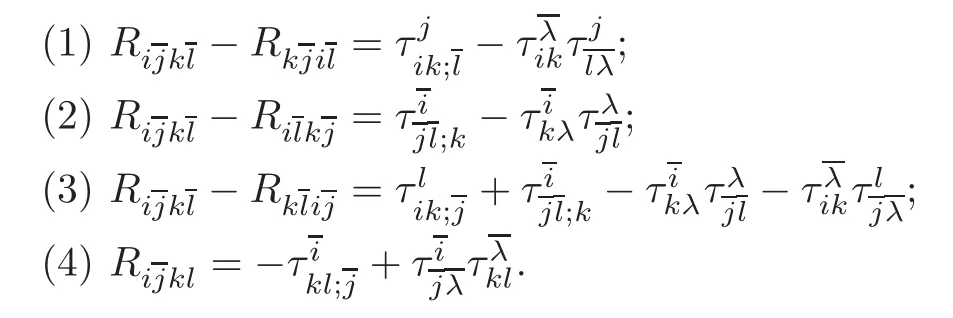
The following general Ricci identity for commuting indices of covariant derivatives is useful for computation.One can find it in[10].

Lemma 2.1 Let Mnbe a smooth manifold,and E be a vector bundle on M.Let D be a connection on E and ∇ be a connection on M with torsion τ.Then

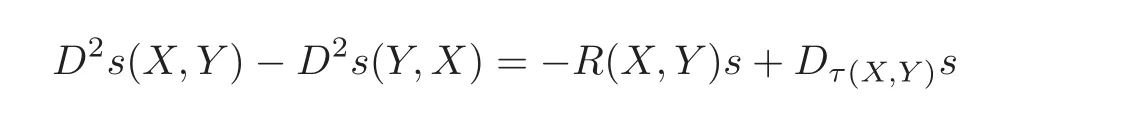
for any cross section s of E,and tangent vector fields X and Y.

Applying Lemma 2.1 to E= ⊗rT∗M,we have the following corollary.

Corollary 2.1 Let(Mn,g)be a Riemannian manifold and D be a connection on M compatible with g and with torsion τ.Let Ta1a2···arbe a tensor on M.Then

Directly by the Corollary 2.1,we have

and

for any smooth function f on almost Hermitian manifolds since=0.

Moreover,recall the following difference of Levi-Civita connection and another compatible connection on Riemannian manifolds.

Lemma 2.2(see[10,12,30])Let(M,g)be a Riemannian manifold and D be the Levi-Civita connection.Let ∇ be another connection on M compatible with g and with torsion τ.Then

By using Lemma 2.2 directly,we have the following relation of the Hessian and divergence operators with respect to the Levi-Civita connection and another compatible connection.

Lemma 2.3 Let(M,g)be a Riemannian manifold and D be the Levi-Civita connection.Let ∇ be another connection on M compatible with g and with torsion τ.Let f be a smooth function.Then

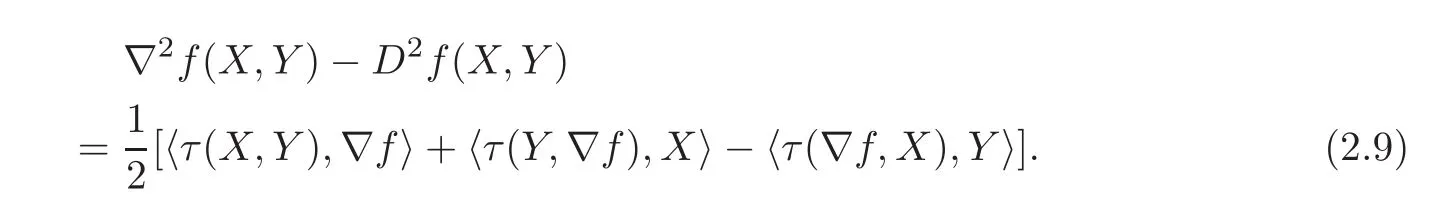
Proof By the definition of Hessian,we have

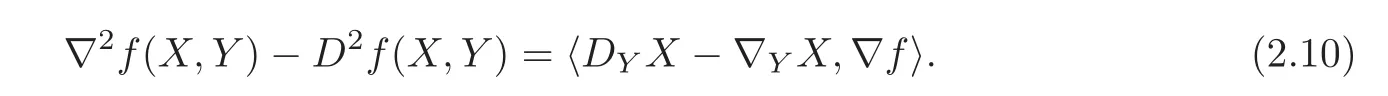
Then,Lemma 2.2 gives us the conclusion directly.

Applying Lemma 2.3 to almost Hermitian manifolds,we get the following corollaries.

Corollary 2.2 On an almost Hermitian manifold, fixed a unitary frame,

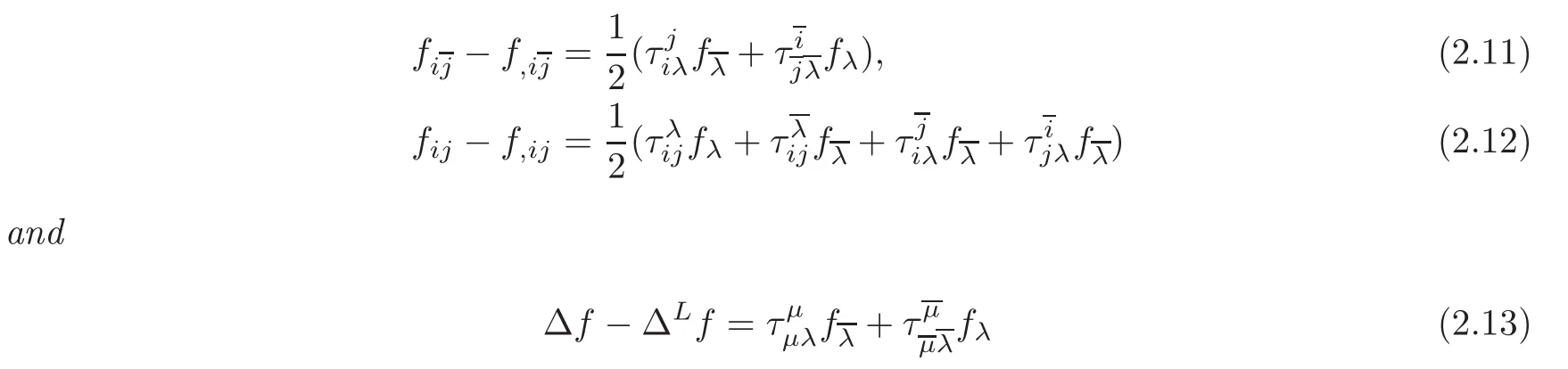
where “,” means taking covariant derivatives with respect to the Levi-Civita connection and ∆Lis the Laplacian operator with respect to the Levi-Civita connection.

Similarly,we have the following comparison of divergence operators.

Lemma 2.4 Let X be a vector field on an almost Hermitian manifold M and fixed a unitary frame.Then

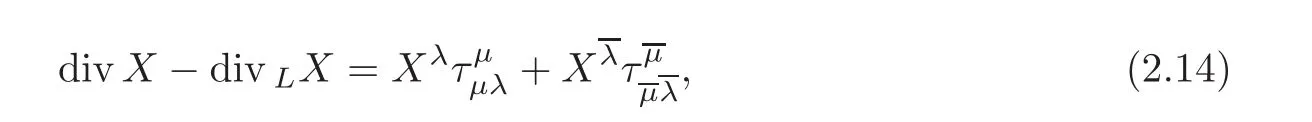
Next,recall the definition of quasi Kähler manifolds.

Definition 2.3 An almost Hermitian manifold(M,J,g)is called a quasi Kähler manifold

The following criterion for quasi Kählerity is well known.

Proposition 2.2(see[19,30])Let(M,J,g)be an almost Hermitian manifold.Then,it is quasi Kähler if and only iffor any i,j and k.

Applying Proposition 2.2 to Proposition 2.1,we have the following first Bianchi identities on quasi Kähler manifolds.

Corollary 2.3 Let(M,J,g)be an quasi Kähler manifold.Fixed a unitary frame,we have

Applying Proposition 2.2 to Corollary 2.2 and Lemma 2.4,we have the following corollary.

Corollary 2.4 Let(M,g,J)be a quasi Kähler manifold.Thenand divX=divLX.

Finally,recall the definition of nearly Kähler manifolds.

Definition 2.4 Let(M,J,g)be an almost Hermitian manifold.It is called nearly Kähler if(DXJ)X=0 for any tangent vector X.

For nearly Kähler manifolds,the difference between canonical connection and Levi-Civita connection becomes simpler.

Lemma 2.5(see[16])Let(M,J,g)be a nearly Kähler manifold.Then

for any tangent vector fields X and Y.In particular,

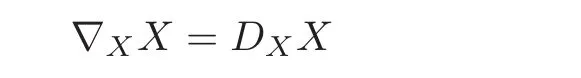
for any tangent vector field X.

The following criterion for nearly Kähler manifold is well known,see for example[24–25].

Lemma 2.6 An almost Hermitian manifold(M,J,g)is nearly Kähler if and only iffor all i,j and k when we fix a(1,0)-frame.

Nearly Kähler manifolds have an important property,that is,the torsion of the canonical connection is parallel.

Theorem 2.1(see[18,32])Let(M,J,g)be a nearly Kähler manifold.Then ∇τ=0.

Applying Lemma 2.6 and Theorem 2.1 to Proposition 2.1,we have the following first Bianchi identities for nearly Kähler manifolds.

Corollary 2.5 Let(M,J,g)be a nearly Kähler manifold and fixed a unitary frame.Then

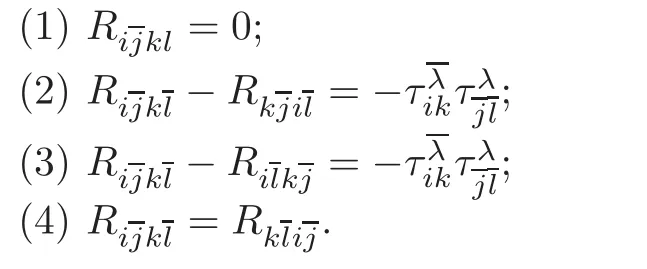
By(4)of the above corollary,the first Ricci curvature and second Ricci curvature for nearly Kähler manifolds coincides,so we simply denote them as Rij.

3 Hessian Comparison and Diameter Estimate on Almost Hermitian Manifolds

In this section,we generalize the results in[22,28–29]to almost Hermitian manifolds.The same as in Tosatti[29],we make the following definition about the bound-ness of the curvatures of an almost Hermitian manifold.

Definition 3.1 Let(M,J,g)be an almost Hermitian manifold.We say that the holomorphic bisectional curvature of(M,J,g)is bounded from below by K if

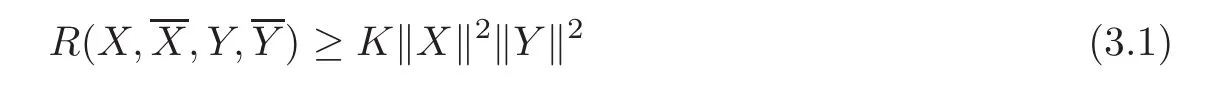
for any X,Y∈T1,0M.We say that the torsion of(M,J,g)is bounded by A1if

for any X,Y∈T1,0M.We say that the(2,0)part of the curvature tensor of(M,J,g)is bounded by A2if

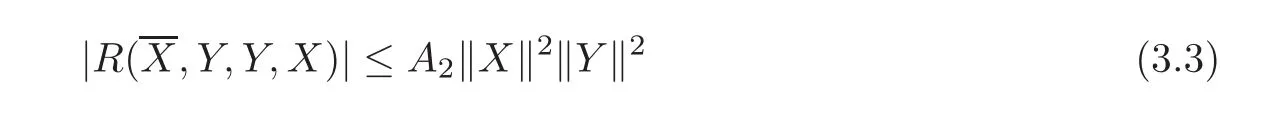
for any X,Y∈T1,0M.

Let(M,J,g)be an almost Hermitian manifold.We denote its distance function to a fixed point o as ρ.Similarly as in Li-Wang[22],we have the following.

Lemma 3.1 Fixed a unitary frame(e1,e2,···,en),we have

Proof Note that ρλρλ=.Hence

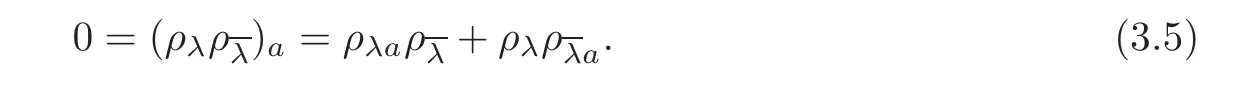
Lemma 3.2 Fixed a unitary frame(e1,e2,···,en),we have

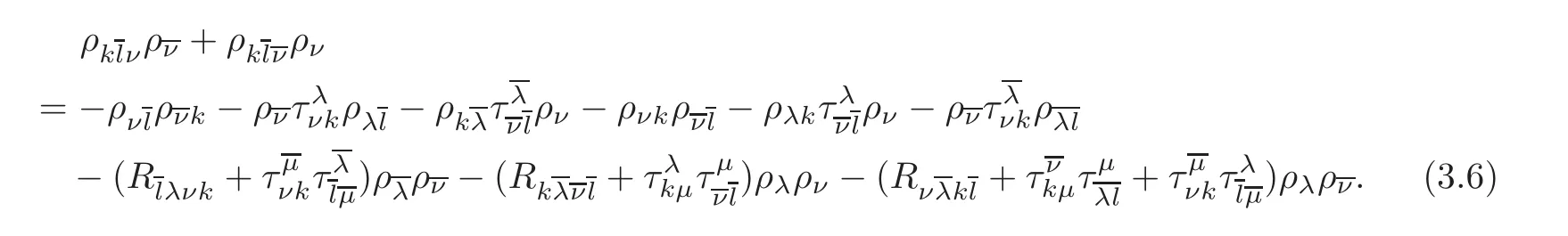
Proof Note that ρνρν=.Hence

where we have used Proposition 2.1 and Corollary 2.1.This completes the proof.

Theorem 3.1 Let(M,J,g)be a complete almost Hermitian manifold with holomorphic bisectional curvature bounded from blow by−K with K ≥0,torsion bounded by A1and the(2,0)part of the curvature tensor bounded by A2.Then

within the cut-locus of o,where

Proof Let γ be a normal geodesic starting from o.Let(e1,e2,···,en)be a parallel unitary frame along γ.Let

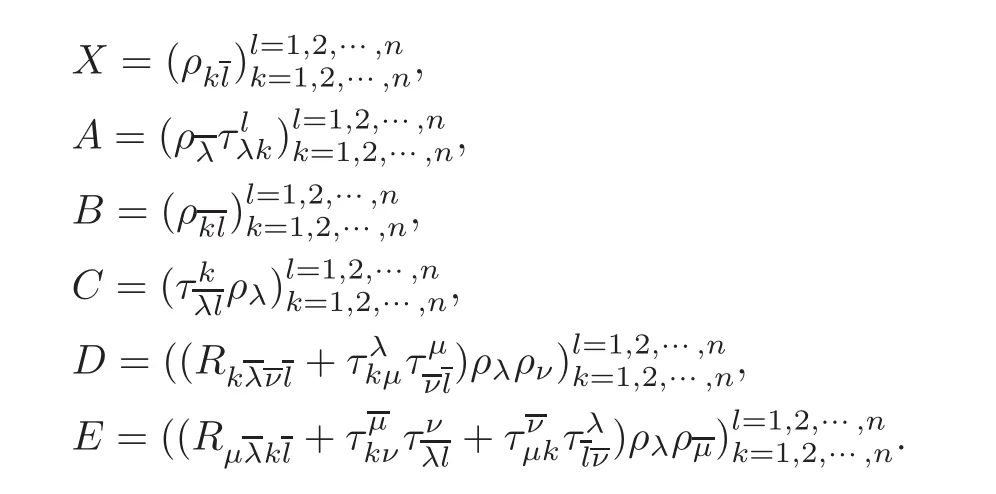
Then,by Lemma 3.2,we know that

Moreover,for any column vector u,we have

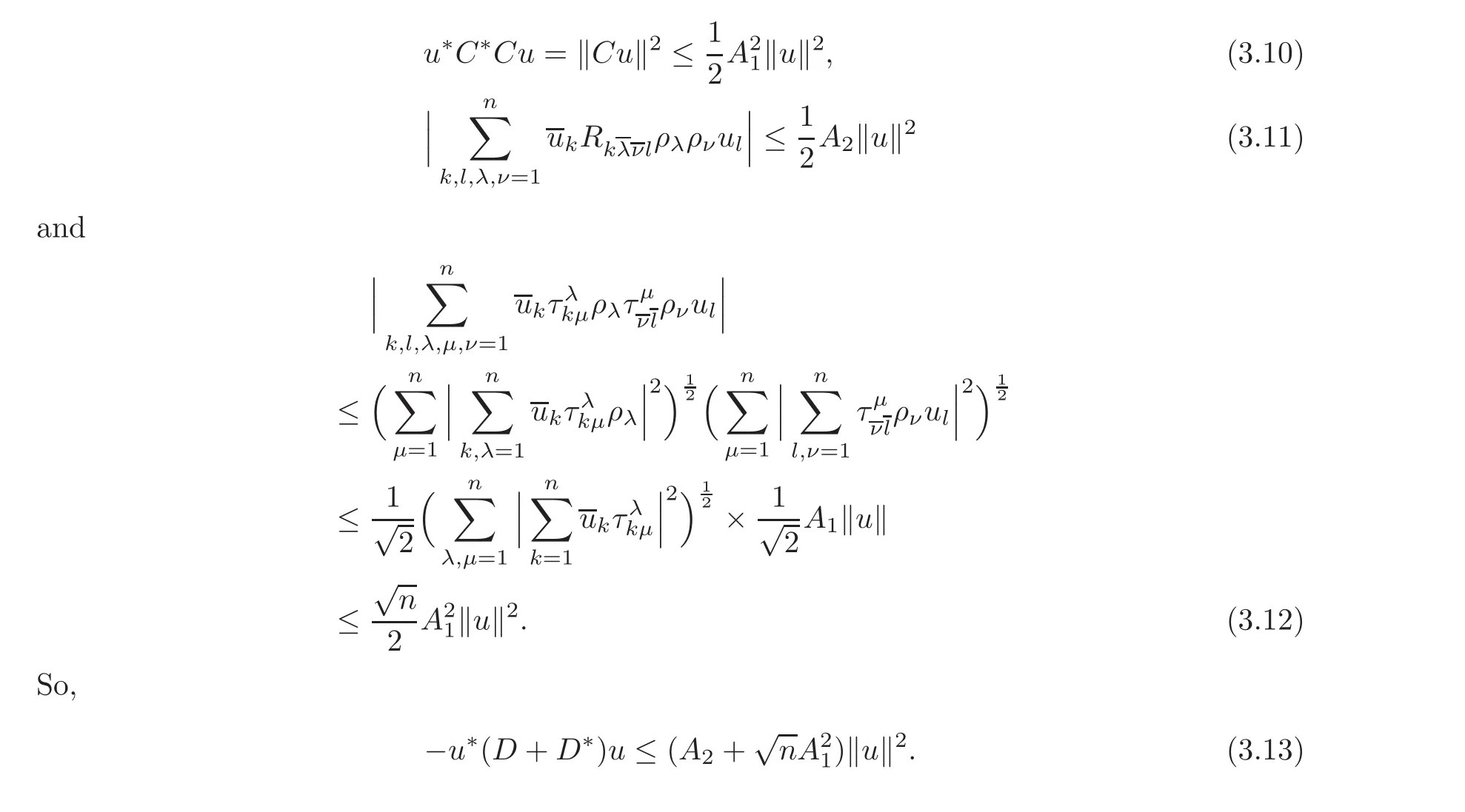
Furthermore,

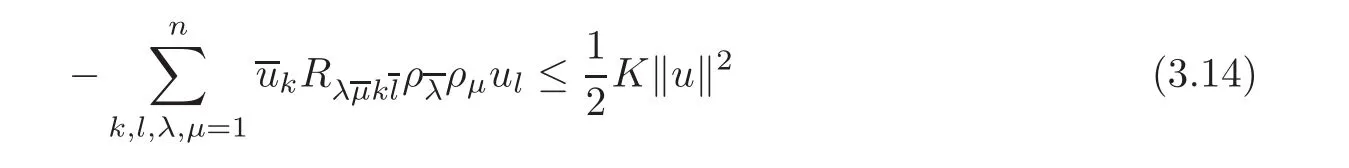
and,similar as in(3.12)

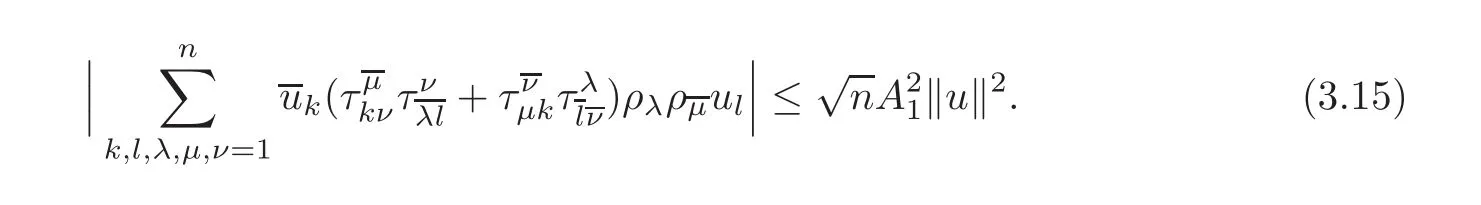
Hence

Combining(3.9)–(3.10),(3.13)and(3.16),we get

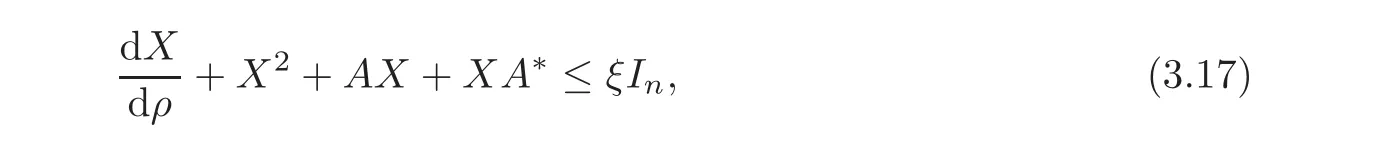
where

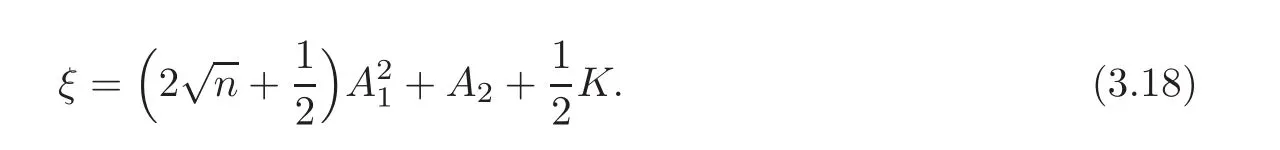
Moreover,by Corollary 2.2,and that

as ρ → 0+(see for example[28]),we have

as ρ → 0+.

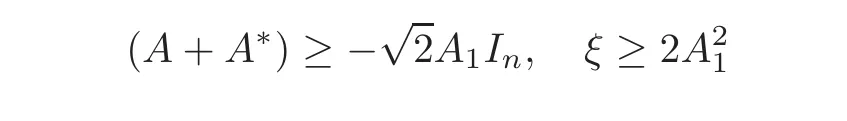
and(3.17).We have

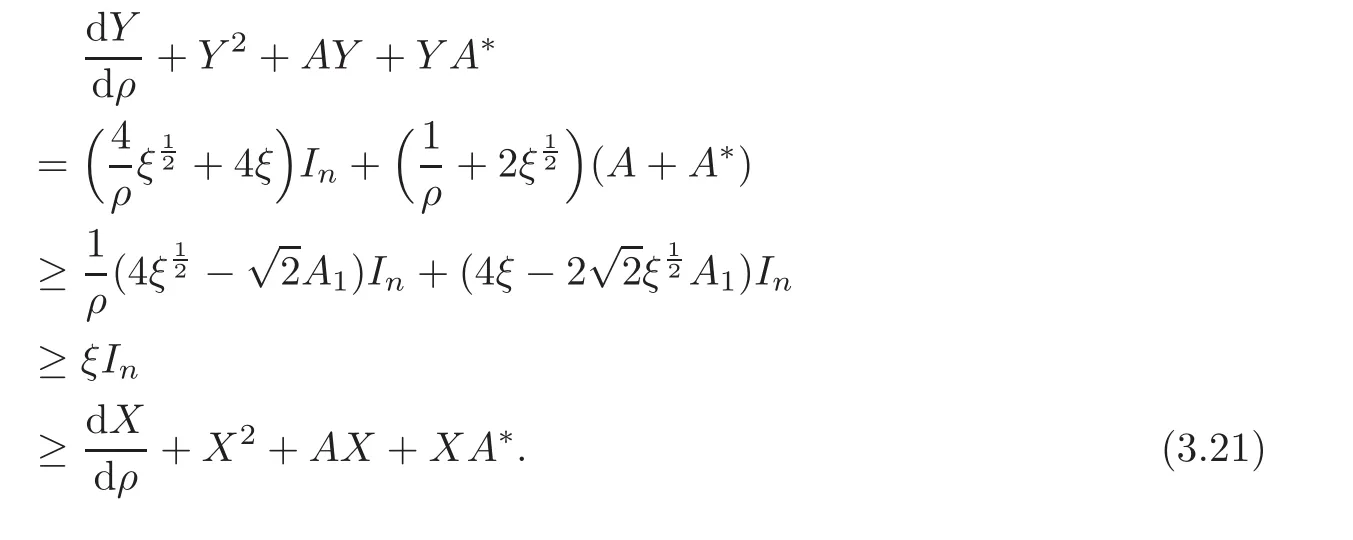
Moreover,

as ρ → 0+by(3.20).By comparison of matrix Ricatti equations in[27],we have

for all ρ within the cut-locus of o.This completes the proof of the theorem.

In the following,we give a sharp diameter estimate for almost Hermitian manifolds.We first extend the notion of quasi-holomorphic sectional curvature in[4]for Hermitian manifolds to almost Hermitian manifolds.

Definition 3.2 Let(M,J,g)be an almost Hermitian manifold.Let X be a real unit vector on M.Define the quasi holomorphic sectional curvature QH(X)as

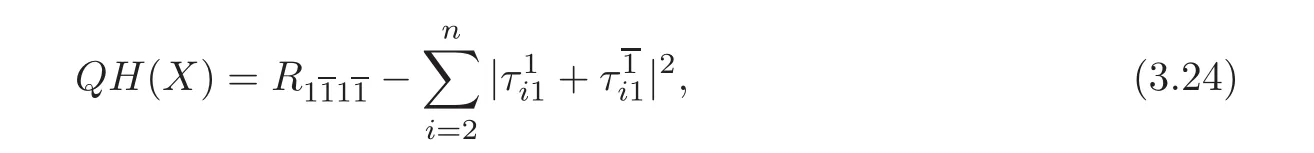
where we have fixed a unitary frame(e1,e2,···,en)with

Remark 3.1 When the complex structure is integrable,the definition of quasi holomorphic sectional curvature is the same as that in[4].

Theorem 3.2 Let(M,J,g)be a complete almost Hermitian manifold and the quasi holomorphic sectional curvature is not less than K>0.Then d(M)

Proof Fixed a unitary frame(e1,e2,···,en),using Lemmas 3.1–3.2,noting that τ and R are both skew symmetric,we have

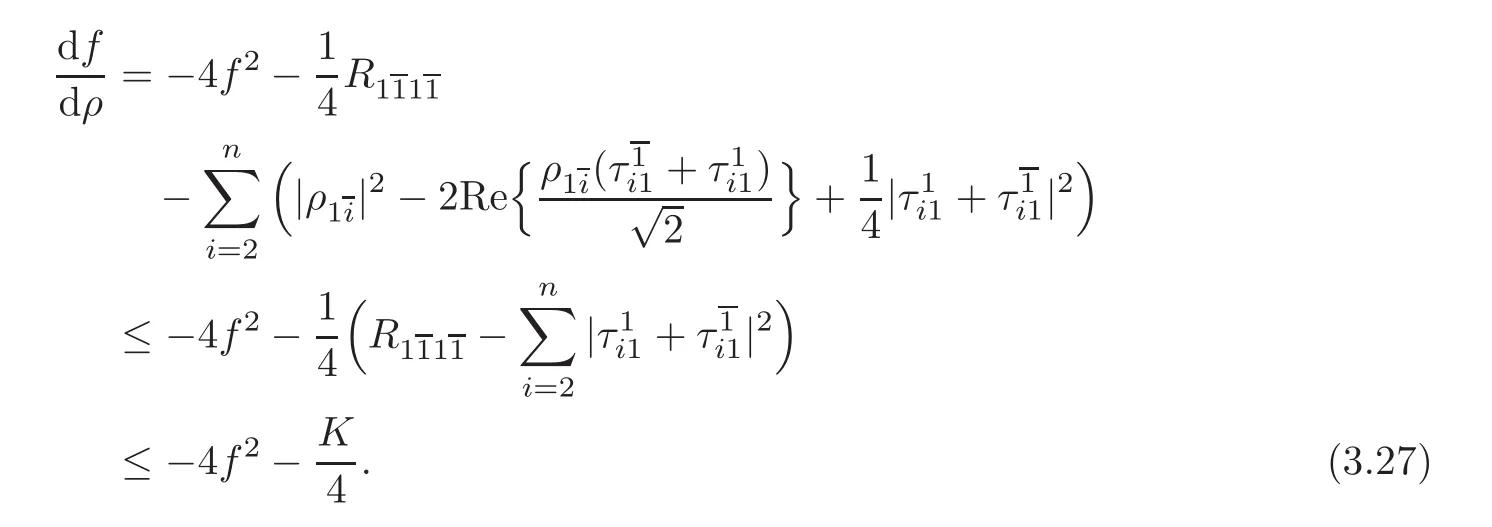
Moreover,by Corollary 2.2,we have

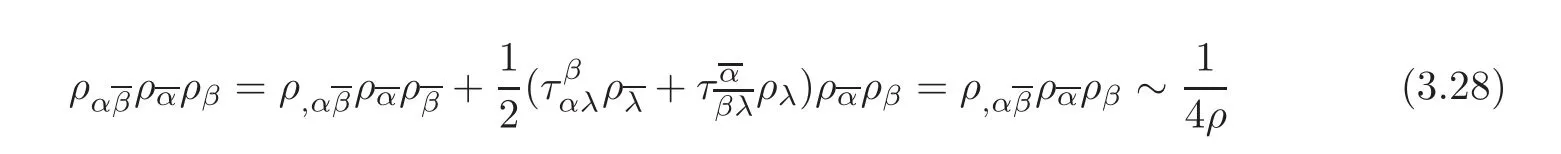
as ρ → 0.By comparison of Riccati equation in[27],we know that

Hence,by a classical argument(see for example[21]),we get the conclusion.

Remark 3.2 The diameter estimate above was disguised with a seemingly different curvature assumption in[14].Indeed,using the curvature identities in[32],one can find that the two curvature assumptions in[14]and in the above are the same.

4 First Eigenvalue Estimate for Quasi Kähler Manifolds

In this section,we give a sharp first eigenvalue estimate for compact quasi Kähler manifolds.

By Corollary 2.4,we know that∆ coincides with ∆Lfor quasi Kähler manifolds.By the same technique as in[2,11],we have the following sharp spectrum lower bound for compact quasi Kähler manifolds which generalizes a similar estimate on compact Kähler manifolds of Aubin[2].Before stating the result,we need the following definition of quasi Ricci curvature.

Definition 4.1 Let(M,J,g)be a quasi Kähler manifold and let

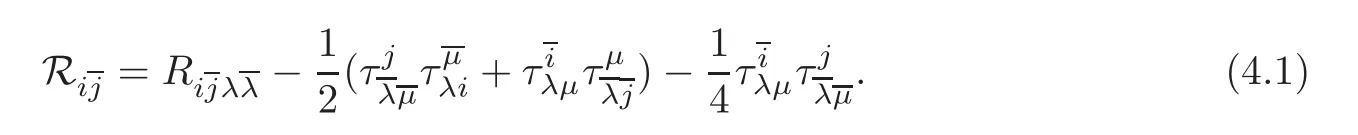
We call Rijthe quasi Ricci curvature.

Theorem 4.1 Let(M,J,g)be a compact quasi Kähler manifold with quasi Ricci curvature bounded from below by a positive constant K.Then λ1≥ 2K,where λ1is the first eigenvalue for the Laplacian operator of(M,g).

Proof Let f be an first eigenfunction for the Laplacian operator.Then

Fixed a unitary frame(e1,e2,···,en),using the Corollaries 2.1 and 2.3–2.4,we know that

Hence

For the equality case,we come to show that the equality can also be achieved by non-Kähler manifolds.Let S6be equipped with the standard almost complex structure and standard Riemannian metric.Then,S6becomes a nearly Kähler manifold.For this nearly Kähler manifold,By the curvature identity

in[32],we have

Therefore,the quasi Ricci curvature

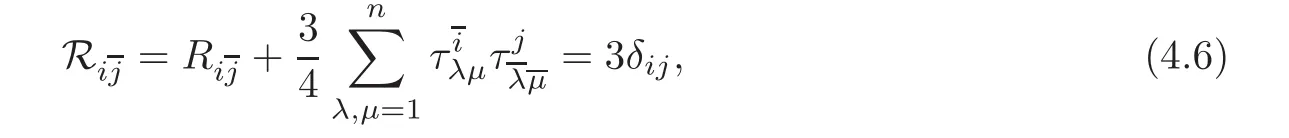
where we have used Lemma 2.6.So,the constant K in the last theorem is 3.It is clear that the first eigenvalue of the standard metric on S6is 6.So,equality of the last theorem is achieved by the nearly Kähler manifold S6.

5 Sharp Hessian Comparison on Nearly Kähler Manifolds

In this section,by using the Bochner technique in[22],we obtain a sharp Hessian comparison on nearly Kähler manifolds generalizing the results of[22,28].

Lemma 5.1 Let(M,J,g)be a complete nearly Kähler manifold,o be a fixed point and ρ(x)be the distance from x to o.Let γ be a normal geodesic starting from o.Let(e1,e2,···,en)be a unitary frame parallel along γ with respect to the canonical connection withfor all i>1 andin the cut-locus of o,for all i≥ 1.

and

for all i>1.By these and Lemma 3.1,we know that

for all i≥1.

Before stating the sharp Hessian comparison on nearly Kähler manifolds,we introduce the following notion of quasi holomorphic bisectional curvature.

Definition 5.1 On a nearly Kähler manifold,define

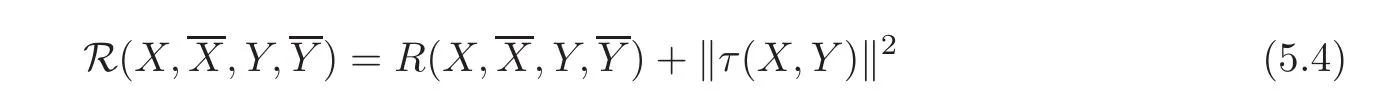
for any(1,0)vectors X and Y.We say that the quasi holomorphic bisectional curvature of M is not less than K if

for any two nonzero(1,0)vectors X and Y.

Theorem 5.1 Let(M,J,g)be a complete nearly Kähler manifold and o be a fixed point in M.Let Bo(R)be a geodesic ball within the cut-locus of o.Suppose that the quasi holomorphic bisectional curvature on Bo(R)is not less than K where K is a constant.Then

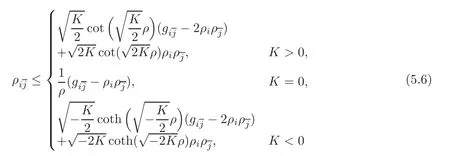
in Bo(R)with equality holds all over Bo(R)if and only if Bo(R)is holomorphic and isometric equivalent to the geodesic ball with radius R in the Kähler space form of constant holomorphic bisectional curvature K,where ρ is the distance function to the fixed point o.

Proof Let γ be a geodesic starting from o,and(e1,e2,···,en)be the same as in Lemma 5.1.Then,by Lemmas 2.6,3.2 and 5.1,and Corollary 2.5,we know that

and X1be the first column of X.Then

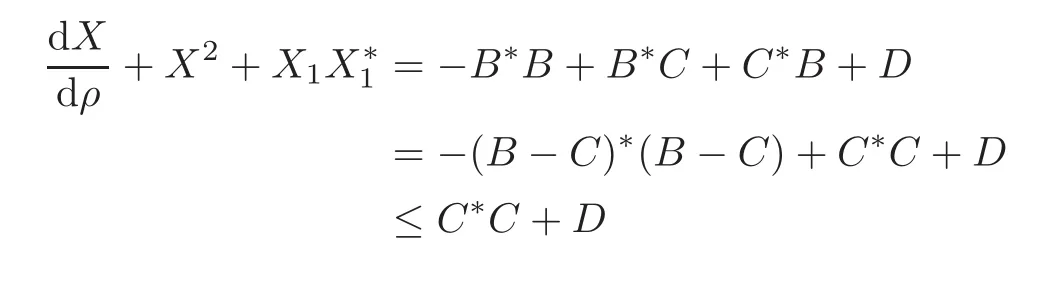
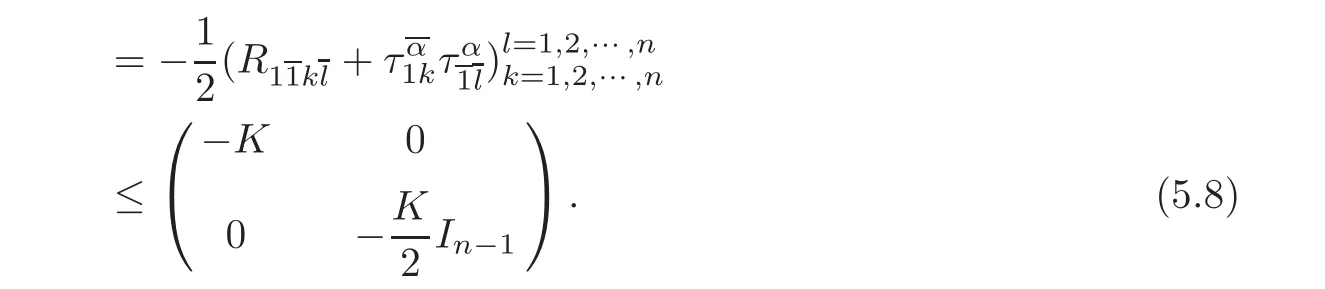
At this position,by the same argument as in[28],we have

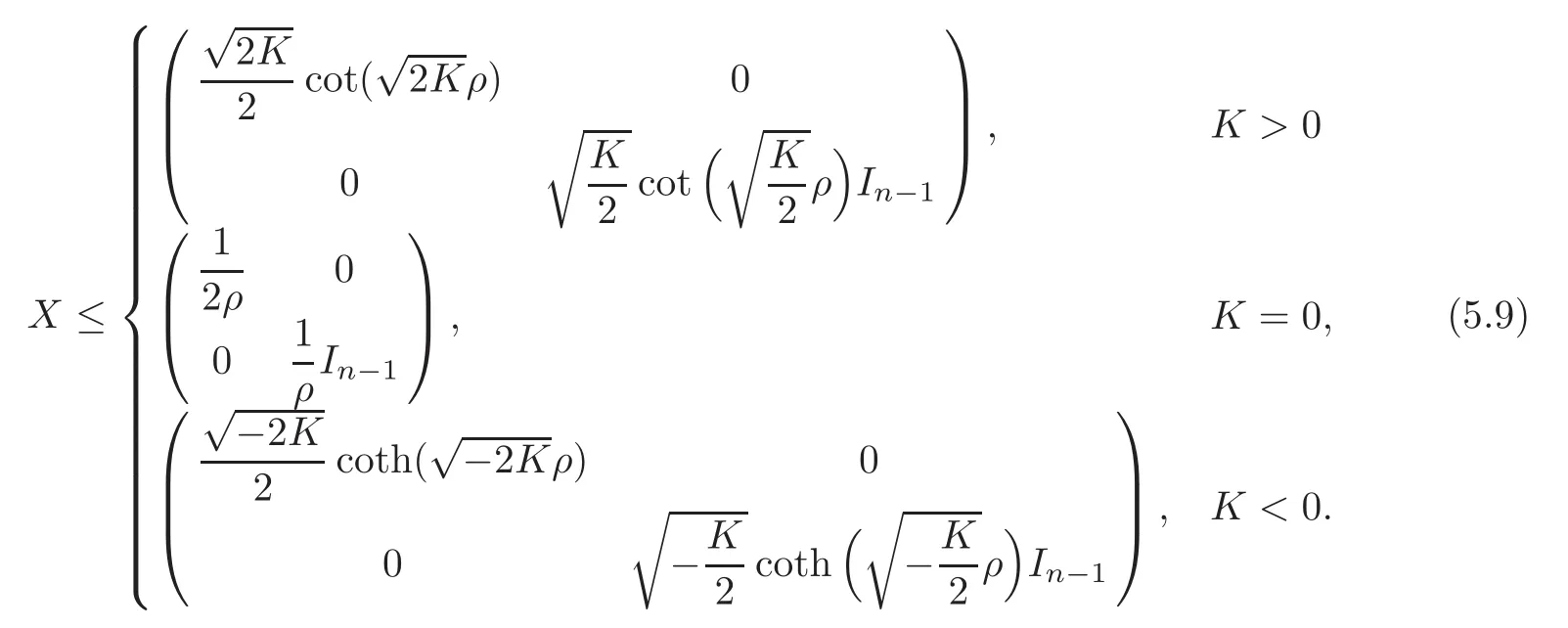
This is the inequality in the conclusion of the theorem.

If the equality holds,we havefor k,l=2,3,···,n.By(2.8),we have

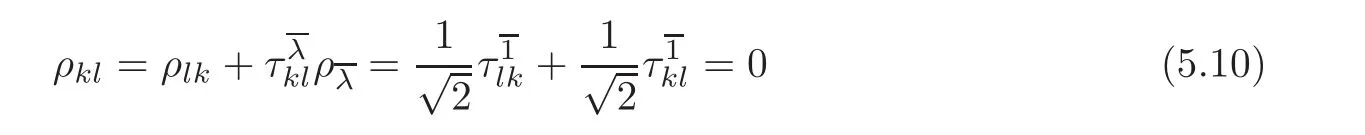
for all k,l=2,3,···,n.Hence

for all k,l=1,2,···,n.In particular,we have

By Theorem 2.1,we know that τ=0 and hence(M,J,g)is Kähler.Then by the equality case of the sharp Hessian comparison for Kähler manifolds in[28],we obtain the conclusion when equality holds.

By the Hessian comparison,we have the following direct corollary on Laplacian comparison.

Corollary 5.1 Let(M,J,g)be a complete nearly Kähler manifold and o be a fixed point in M.Let Bo(R)be a geodesic ball within the cut-locus of o.Suppose that the quasi holomorphic bisectional curvature on Bo(R)is not less than K where K is a constant.Then

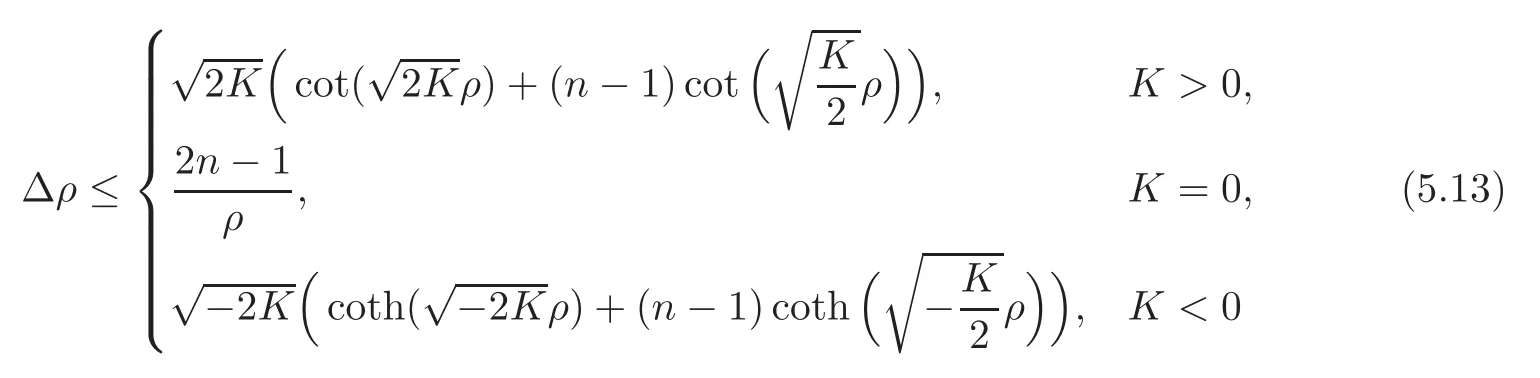
in Bo(R)with equality holds all over Bo(R)if and only if Bo(R)is holomorphic and isometric equivalent to the geodesic ball with radius R in the Kähler space form of constant holomorphic bisectional curvature K,where ρ is the distance function to the fixed point o.

By the same argument as in[5](see also[21]),we have the following comparison of first eigenvalue and volume comparison for nearly Kähler manifolds.

Corollary 5.2 Let(M,J,g)be a complete nearly Kähler manifold and o be a fixed point in M.Let Bo(R)be a geodesic ball within the cut-locus of o.Suppose that the quasi holomorphic bisectional curvature on Bo(R)is not less than K where K is a constant.Then

where BK(R)is the geodesic ball with radius R in the Kähler space form with constant holomorphic bisectional curvature K.Moreover,if the equality holds,then Bo(R)and BK(R)are holomorphically isometric to each other.

Corollary 5.3 Let(M,J,g)be a complete nearly Kähler manifold and o be a fixed point in M.Let Bo(R)be a geodesic ball within the cut-locus of o.Suppose that the quasi holomorphic bisectional curvature on Bo(R)is not less than K where K is a constant.Then

where VK(R)is the volume of BK(R).Moreover,if the equality holds,then Bo(R)and BK(R)are holomorphically isometric to each other.

Corollary 5.4 Let(M,J,g)be a complete nearly Kähler manifold with quasi holomorphic bisectional curvature≥K with K>0.Then

AcknowledgementThe author would like to thank the referees for helpful comments and suggestions.