Endpoint Estimates for Generalized Multilinear Fractional Integrals on the Non-homogeneous Metric Spaces∗
Jiecheng CHENXiaoli CHENFangting JIN
Abstract In this paper,some endpoint estimates for the generalized multilinear fractional integrals Iα,mon the non-homogeneous metric spaces are established.
Keywords Generalized multilinear fractional integrals,Lipschitz space,RBMO space,Morrey space,Non-homogeneous metric space
1 Introduction and Notation
Spaces of homogeneous type—(quasi-)metric spaces equipped with a so-called doubling measure—were introduced by Cofiman and Weiss[7]as a general framework in which many results from real and harmonic analysis on Euclidean spaces have their natural extensions(see for example[6,11–12]).It is now well known that a metric space(X,d)equipped with a nonnegative Borel measureµ is called a space of homogeneous type— if(X,d,µ)satifies the following measure doubling condition that there exists a positive constant Cµ,depending on µ,such that for any ball B(x,r)={y∈X:d(x,y) The doubling condition(1.1)plays a key role in the classical theory of Calderón-Zygmund operators. Meanwhile,recent developments in the Calderón-Zygmund theory(which one might think of it as “zeroth order calculus”,as only integrability of the functions on which one operator is considered)have shown that a number of interesting problems cannot be,and need not be,embedded into the homogeneous framework.The measure can be replaced by a less demanding condition such as the polynomial growth condition. Letµbe a non-negative Radon measure on Rnwhich only satisfies the polynomial growth condition,namely,there exist positive constants C and κ ∈ (0,n]such that for all x ∈ Rnandr∈ (0,∞), The analysis associated with such nondoubling measuresµis proved to play a striking role in solving the long-standing open painlevé’s problem by Tolsa[20].Obviously,the measure µsatisfies the polynomial growth condition may not satisfy the doubling condition.To unify both the doubling condition and polynomial growth condition,Hytönen[14]introduced a new class of metric measure spaces satisfying so-called geometrically doubling and the upper doubling conditions(see Definitions 1.1–1.2 respectively),which are called non-homogeneous spaces.We refer the reader to the survey(see[21])and the monograph(see[22])for more progress on the theory of Hardy spaces and singular integrals over nonhomogeneous metric measure spaces. Definition 1.1 A metric measure space(X,d,µ)is called upper doubling ifµ is a Borel measure on X and there exists a dominating function and a positive constant Cλ>1 such that for each x∈X,r→ λ(x,r)is non-decreasing and,for all x∈X and r∈(0,∞), Remark 1.1(i)A space of homogeneous type is a special case of upper doubling spaces,where one can take the dominating function λ(x,r) ≡ µ(B(x,r)).On the other hand,a metric space(X,d,µ)satisfying the polynomial growth condition is also an upper doubling measure space if we take λ(x,r) ≡ Crk. (ii)Let(X,d,µ)be an upper doubling space and λ be a dominating function on X ×(0,+∞)as in Definition 1.1.In[15],it was showed that there exists another dominating functionsuch that for all x,y∈X with d(x,y)≤r, Based on this,in this paper,we always assume that the dominating function λ also satisfies(1.4). Definition 1.2 A metric measure space(X,d)is called geometrically doubling if there exists a positive integer N0such that for any ball B(x,r)⊂X,there exists a finite covering?B?xi,r2?? iof B(x,r)such that the cardinality of this covering is at most N0.In this paper,we will consider the boundedness of generalized multilinear fractional integrals on nonhomogeneous spaces.First,let us give some symbols and notation.We start with the notion of multilinear fractional kernel of order α and regularity δ. Definition 1.3 Let 0<α (i)There exists s positive constant C such that for all x,y1,···,ym∈ X with x 6=yjfor some j, (ii)For all x,x′,y1,···,ym∈ X with max{d(x,y1),···,d(x,ym)} ≥ 2d(x,x′), Now,we will give the definition of the generalized multilinear fractional integral operator Iα,massociated with Kα. Definition 1.4 For 0<α When m=1,the operator Iα,1defined by(1.7)is adapted from the generalized fractional integral operator in nonhomogeneous metric spaces that appeared in[9]withreplacedSee also[13]for the case of Euclidean spaces associated with nondoubling measures. As is well-known,when(X,d,µ)=(Rn,|·|,dx),the classical multilinear fractional integrals operator Iα,mis bounded from L1(Rn) × ···× L1(Rn)intoHowever,in the case of non-homogeneous metric spaces,it is still unknown whether Iα,mhas the(L1(µ) ×-boundedness.It is known that many authors have been interested in studying the boundedness of this operator on various function spaces,see[10],[16],[18]and[5]etc.Recently,Tang[19]studied the classical multilinear fractional integral and obtained some endpoint estimates.He proved that Iα,mis bounded fromto BMO(Rn)In addition,he also obtained the-boudedness andboudedness withSee[8]for more information on the theory of generalized fractional integrals and Hpspaces over non-homogeneous metric measure spaces. Inspired by[9]and[19],we will investigate the same endpoint estimates in[19]for generalized multilinear fractional integral on non-homogeneous metric spaces.We can formulate our main results as follows. Theorem 1.1 Let m ∈ N,(m − 1)n< α Theorem 1.2 Let m ∈ N,0< α Theorem 1.3 Let m ∈ N,0< α Without loss of generality,in this paper,we only consider the case of m=2,and C always means a positive constant independent of the main parameters involved,but it may be different from line to line.The p′is the conjugate index of p,that is to say,1p+1p′=1. The paper is organized as follows.In Section 2,we collect some useful definitions and lemmas.Theorems will be proved in the last section. In this section,we will recall some necessary notions and notation and the boundedness of Iα,2in Ls(µ)which was established in[3].We begin with the definition of(α,β)-doubling ball,which can be found in[14]. Definition 2.1 Let α,β ∈ (1,∞).A ball B ⊂ X is called(α,β)-doubling ifµ(αB)≤ βµ(B).It was proved in[14]that if a metric measure space(X,d,µ)is upper doubling and β >then for every ball B ⊂ X,there exists some j∈ Z+≡ N∪{0}such that αjB is(α,β)-doubling.Moreover,let(X,d)be geometrically doubling,β > αnwith n ≡ log2N0and µ a Borel measure on X which is finite on bounded sets.Hytönen[14]also showed that for µ-almost every x ∈ X,there exist arbitrarily small(α,β)-doubling balls centered at x.Furthermore,the radius of these balls may be chosen to be of the form α−jr for j ∈ N and any preassigned number r ∈ (0,∞).For any α ∈ (1,∞)and ball B,eBαdenotes the smallest(α,βα)-doubling ball of the form αjB with j ∈ N,where In this paper we choose α =6 and denote the ballsimply byeB. Next,we give the definitions of constant KB,Sand regular BMO space RBMO introduced by Bui and Duong[1]. Definition 2.2 For any two balls B⊂S,define where cBis the center of the ball B. Remark 2.1 The following discrete versionof KB,Sdefined in Definition 2.2 was first introduced by Bui and Duong[1]in non-homogeneous metric measure spaces,which is more close to the quantity KQ,Rintroduced by Tolsa[20]in the setting of non-doubling measures.For any two balls B⊂S,letbe defined by where rBand rSrespectively denote the radii of the balls B and S,and NB,Sthe smallest integer satisfying 6NB,SrB≥rS.Then KB,S≤C,but,in general,it is not true that KB,S∼ Now we introduce the fractional coefficientfrom[9];see also[4]for the case of Euclidean spaces associated with non-doubling measures. Definition 2.3 For any two balls B⊂S,is defined by where γ∈(0,1)and NB,Sis defined as in Remark 2.1. Next we give out some properties ofappeared in[9,Lemma 3.4],which are completely analogous to[4,Lemma 3]. Lemma 2.1 Let γ∈(0,1). (ii)For any ρ ∈ [1,∞),there exists a positive constant C(ρ),depending only on ρ,such that for all balls B⊂S with rS≤ ρrB,≤ C(ρ). (iii)There exists a positive constant C(γ),depending on γ,such that for all balls B, (iv)There exists a positive constant c,depending on Cλand γ,such that for all balls B ⊂ (v)There exists a positive constant ec,depending on Cλand γ,such that for all balls B ⊂ Now we give the definition of regular BMO space RBMO introduced by Bui and Duong in[1]. Definition 2.4 Let 1<ρ<∞be some fixed constant.A function b∈is said to belong to RBMO(µ)if there exists a positive constant C>0,such that for any ball B, and for any two doubling balls B,S,such that B⊂S, The minimal constant C appearing in(2.2),(2.3)is defined as the RBMO(µ)norm of f and denoted by kbk∗or kbkRBMO(µ). Now,we recall the definition of function space Lip(β)introduced by Zhou and Wang[23]. Definition 2.5 Suppose that β∈(0,1],we say that the function f:X→C satisfies a Lipschitz condition of order β provided that for every x,y ∈ X and the smallest constant in this inequality will be denoted by kfkLip(β). It is easy to see that the linear space with the norm k.kLip(β)is a Banach space,and we call it Lip(β).The following Morrey Mpq(k,µ)and weak Morrey space W(k,µ)appear in[2];see also[17]. Definition 2.6 Let k>1 and 1≤q≤p<∞.Define Definition 2.7 Let k>1 and 1≤q≤p<∞.We say that f belongs to weak Morrey space W(k,µ)if Cao and Zhou showed in their paper[2]that for different k the Morrey spaces(k,µ)are equivalent with each other. Lemma 2.2 Let k,r>1.Then The following ε-weak reverse doubling condition was introduced by Fu,Yang and Yuan in[9]. Definition 2.8 Let ε ∈ (0,∞).A dominating function λ is satisfying the ε-weak reverse doubling condition if,for all r∈(0,2diam(X))and a∈there exists a number C(a)∈[1,∞),depending only on a,r and X,such that for all x∈X, and moreover, Remark 2.2(i)It is easy to see that if ε1< ε2,then λ also satisfies the ε2-weak reverse doubling condition. (ii)Assume that diam(X)=∞.For any fixed x∈X,we know that (iii)It is easy to see that the ε-weak reverse doubling condition is much weaker than the assumption introduced by Bui and Duong in[1]:There exists m ∈ (0,∞)such that for all x∈ X and a,r∈ (0,∞),λ(x,ar)=amλ(x,r). Finally,we give the(Lq1(µ)×Lq2(µ),Ls(µ))boundedness of general integral operator Iα,2,which can be found in[3]. Lemma 2.3 Suppose 1 In this section,we always suppose that the point x 6=y,B is the ball with center x and radius r=d(x,y),obviously 2B⊂B(y,3r)=3B(y,r).First,we prove Theorem 1.1. Proof of Theorem 1.1 For any ball B⊂X,letj=1,2,and set and for any two(6,β6)doubling balls B ⊂ S, Therefore,to prove Theorem 1.1,it suffices to show that for any ball B, and that for all balls B ⊂ S with S being(6,β6)-doubling, Let us prove(3.3) firstly.Write Therefore,to prove(3.3),we need only to prove thatfor i=1,···,4.Suppose thatfor j=1,2, α = α1+ α2and δ= δ1+ δ2,where δ1,δ2>0.Let us estimate E1first.Forby Hölder’s inequality and Lemma 2.3,we get Now we estimate E2.E3can be done in the same way by notice the fact that λ(x,r) ≤Cλ(y,r)if d(x,y) By the condition(1.6),Hölder’s inequality and(2.9),we also obtain Inequalities from(3.5)to(3.8)yield(3.3). Next,we show(3.4)for chosen hBand hS.Denote the smallest positive integer N such that 2S⊂6NB simply by N1.Write By the size condition(1.5),Hölder’s inequality and the fact thatwe have Hence Similarly,we see that and On the other hand,it follows from(1.5),(1.3)and(1.4)that for all y∈B, which implies Analogously, Now,we estimate F8.F7can be done in the same way.Notice that while,by a familiar argument similar to that used in the estimate for E2, Therefore Finally,using the same method that appeared in the estimate for E4,we can get Combining all the estimates for Fiwith i=1,···,9,we get(3.9),which completes the proof of Theorem 1.1. Proof of Theorem 1.2 For any x,y∈X,it suffices to prove Write Secondly,we estimate G3and G4.Using the fact thatan argument similar to that used in the estimate for E2,we have Finally,we estimate G5.Applying the same method to estimate E4,we can get Combining inequalities(3.13)to(3.16),we finish the prove of equality(3.12),so we havefinished the prove of Theorem 1.2. Proof of Theorem 1.3 To prove the inequalities(1.10)and(1.11),we need only to prove and respectively. We estimate H1to H4respectively.Using the fact thatand Lemma 2.2,we have By the same method to that used in the estimate for E2in the case=0 and noticing the fact thatand 0<α<2n,we have Thus Similarly By the same method to that used in the estimate for E4in the case thatone gets So Therefore(3.17)has been proved. Next,we prove(3.18),write We first estimate M1.Due to the fact thatLemma 2.3 and Lemma 2.2, So Now,we estimate M2.M3can be done in the same way.By Lemma 2.3 and inequality(3.21), Hence Due to inequality(3.24),we can get Thus Therefore we have finished the prove of Theorem 1.3. AcknowledgementThe authors would like to thank the referee for his/her suggestions.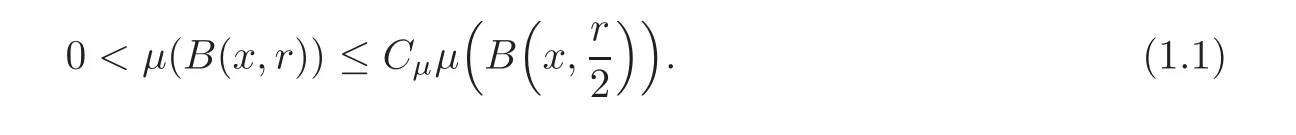
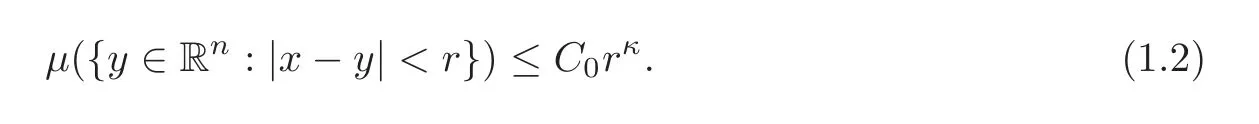

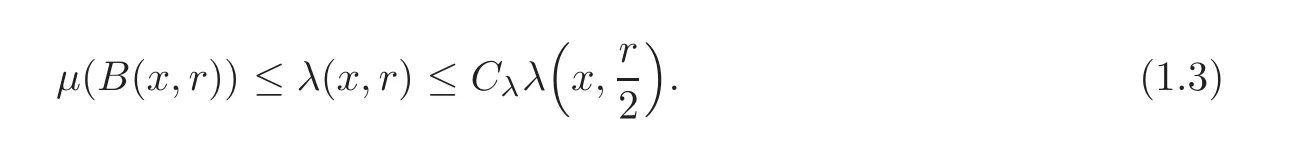

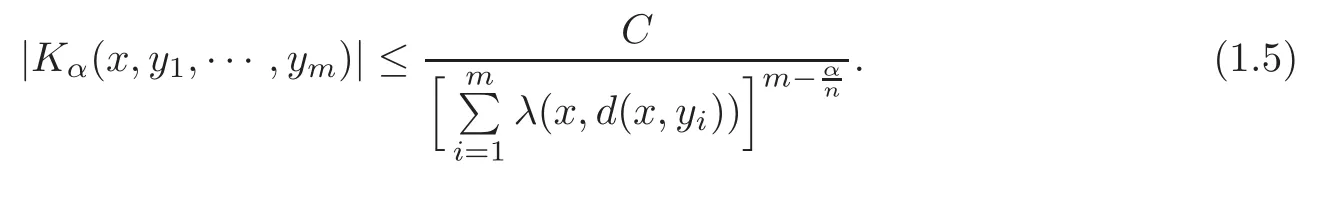
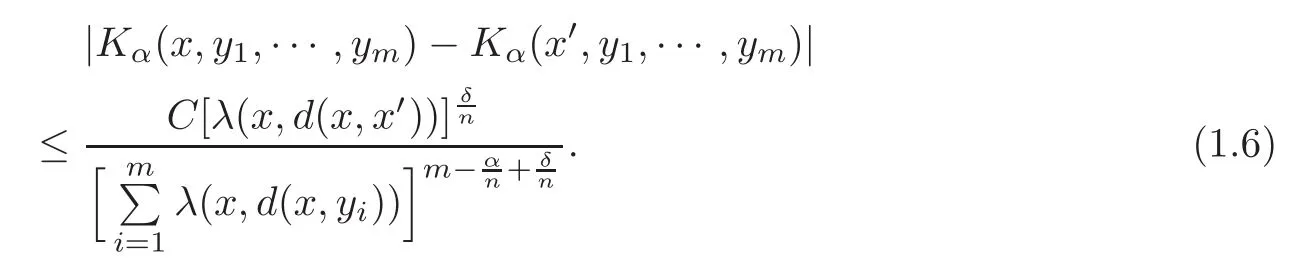
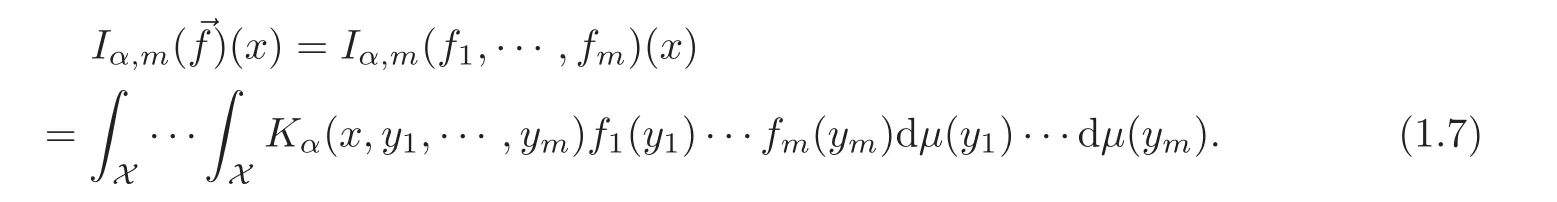
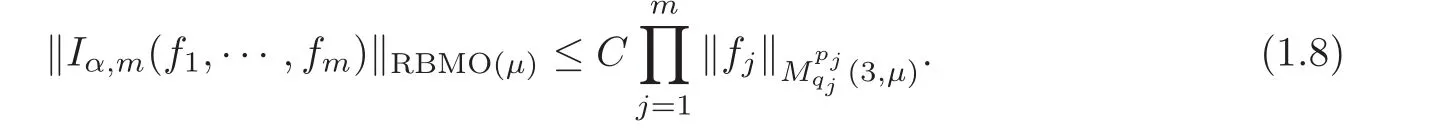

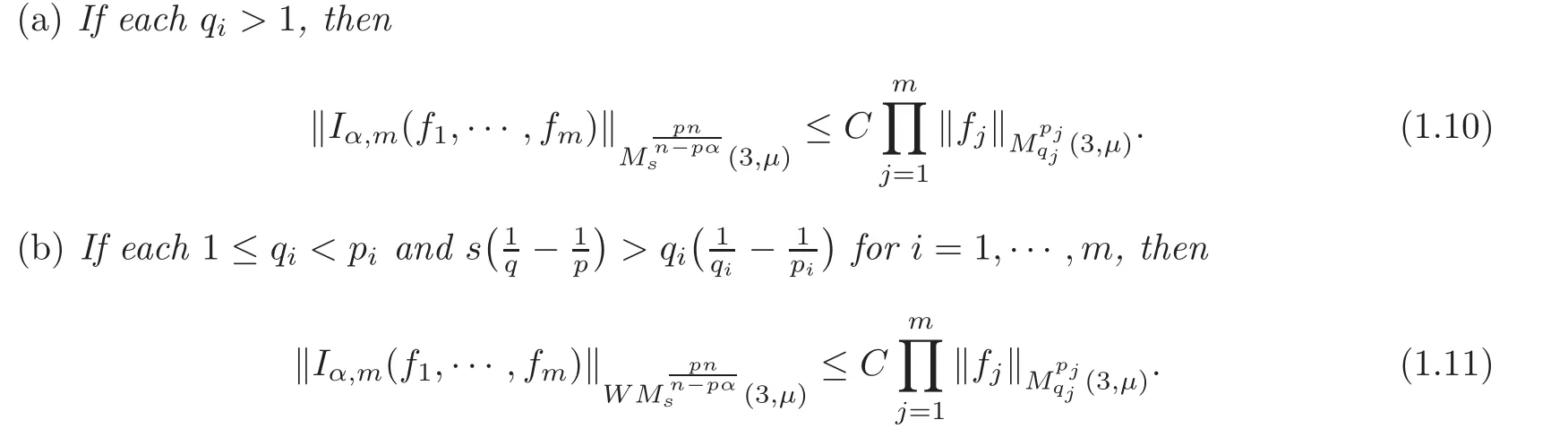
2 Preliminaries
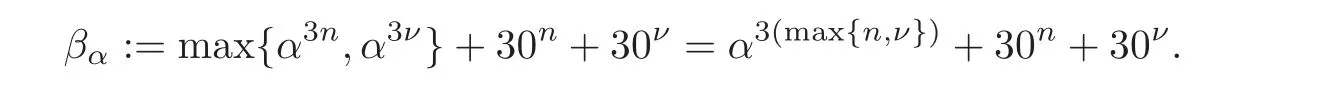

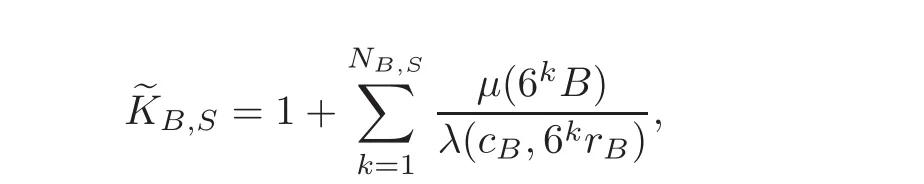
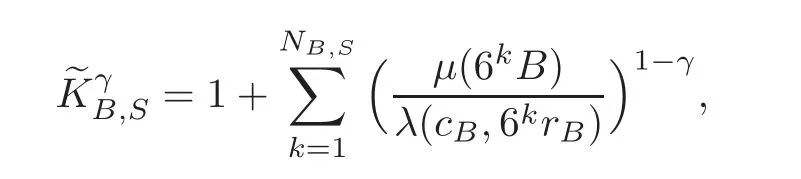
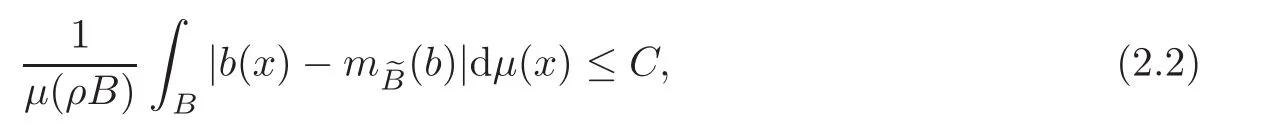
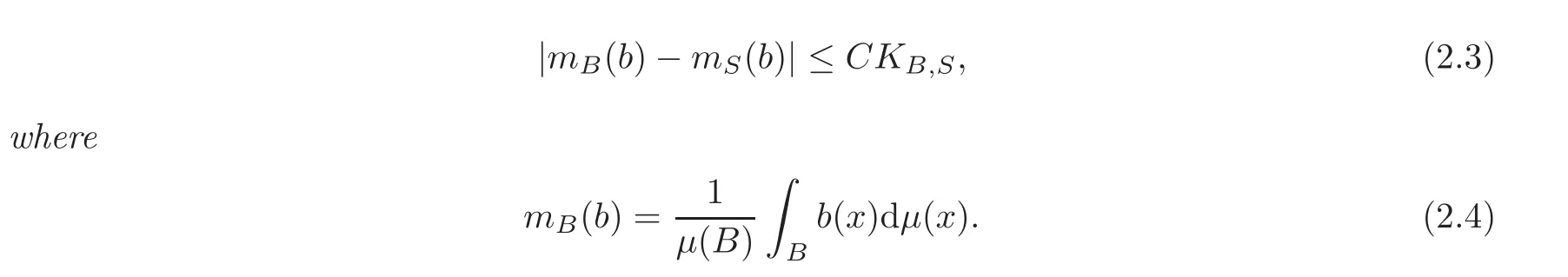

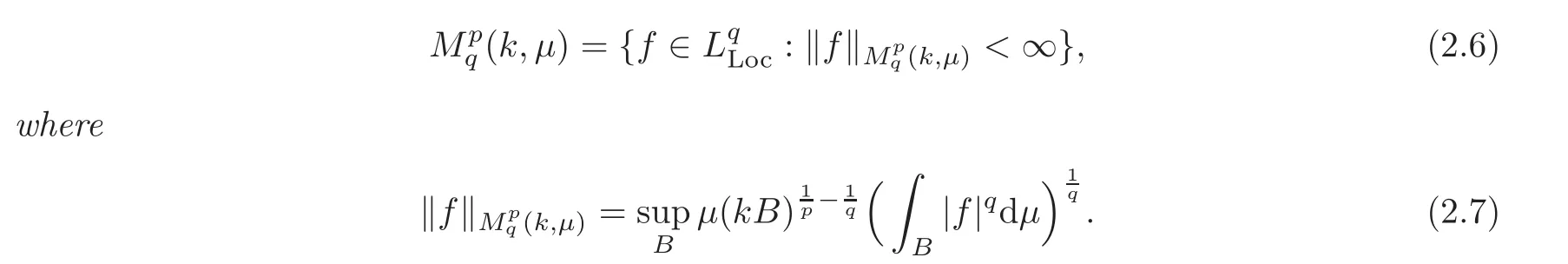
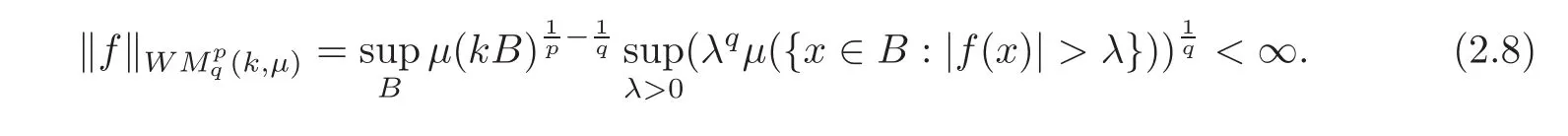



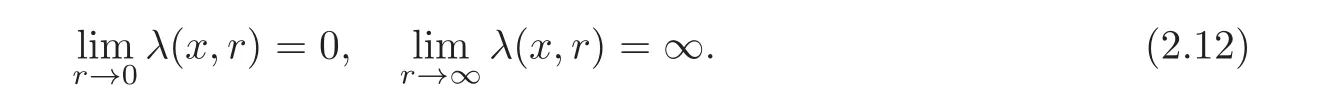
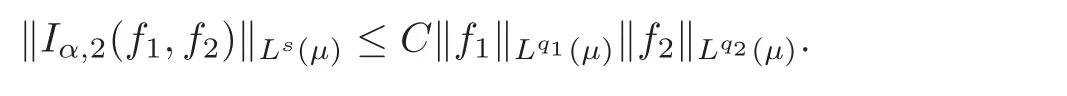
3 The Proofs of Theorems 1.1–1.3
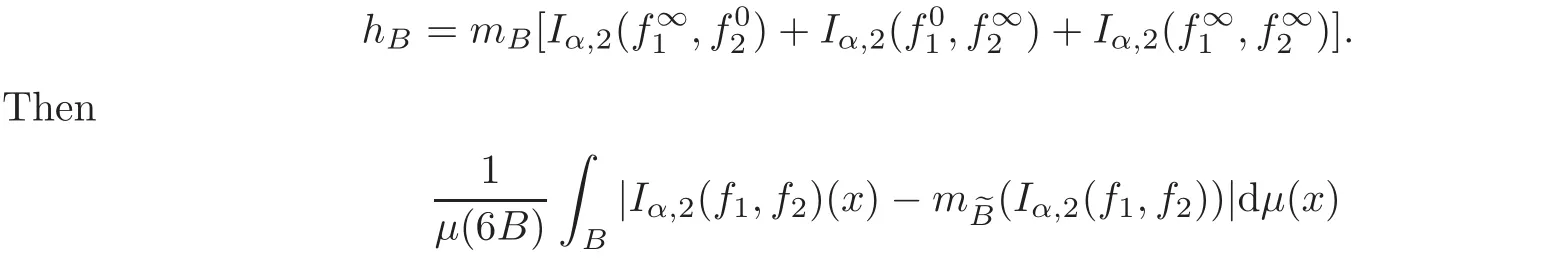

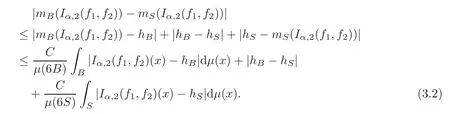
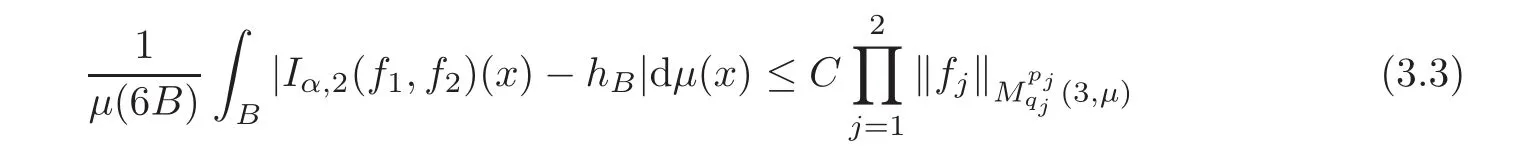
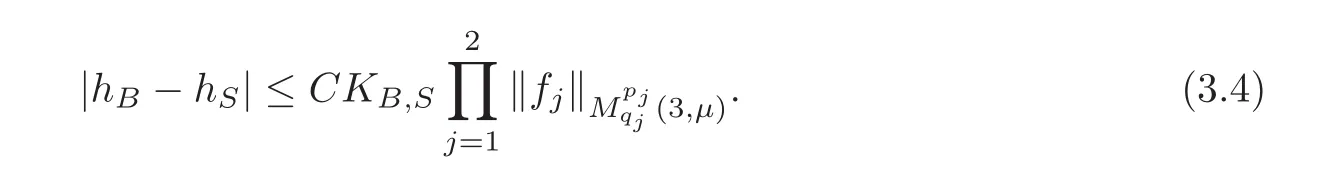
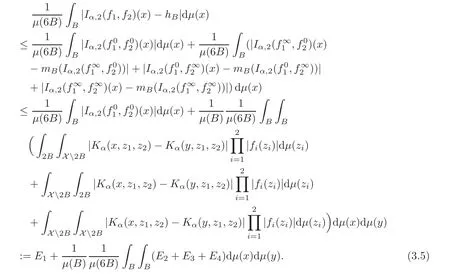
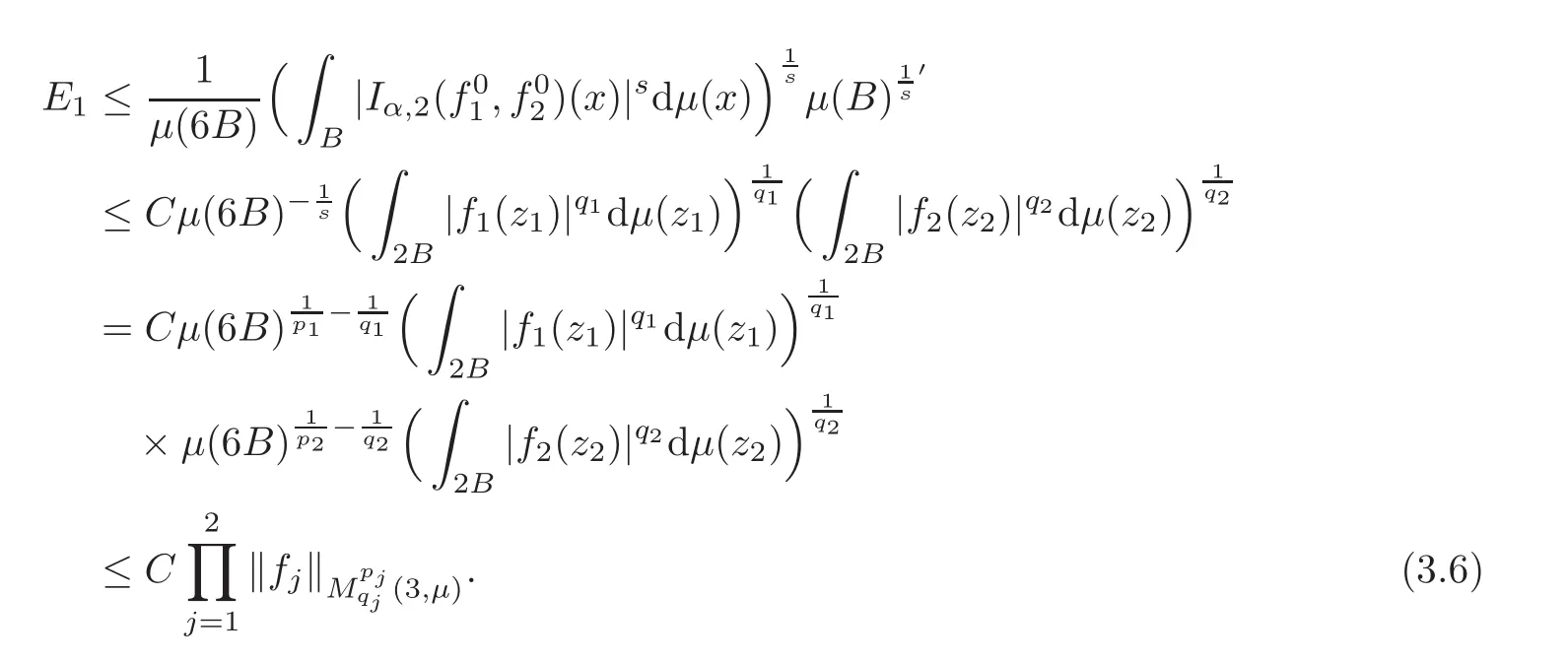

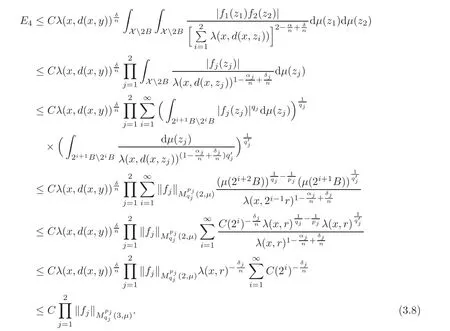
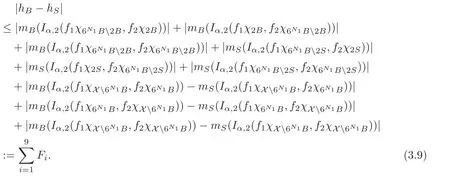

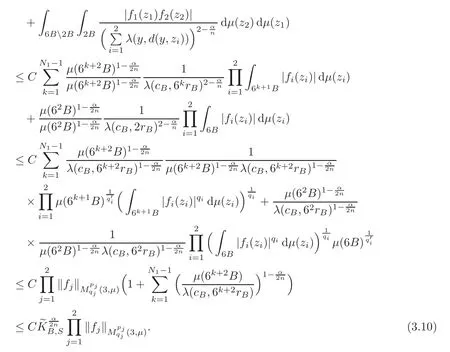
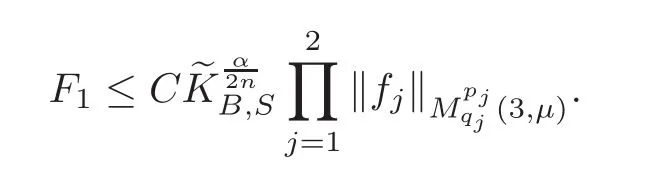
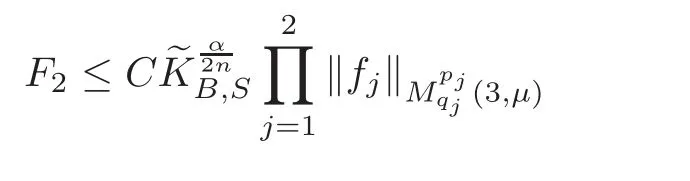
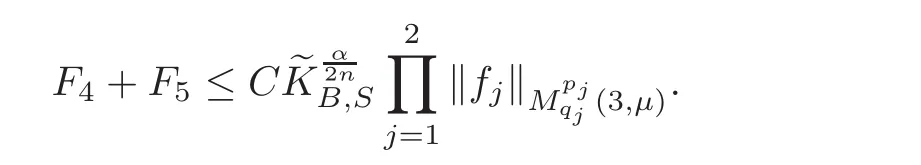
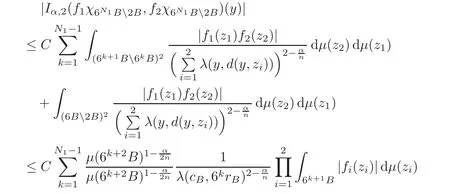
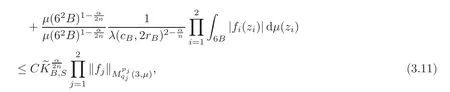

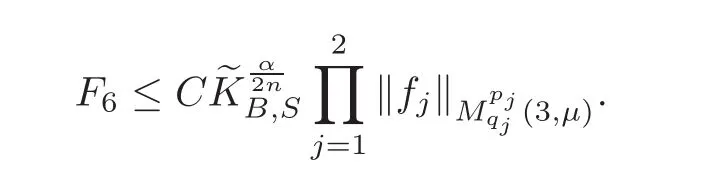
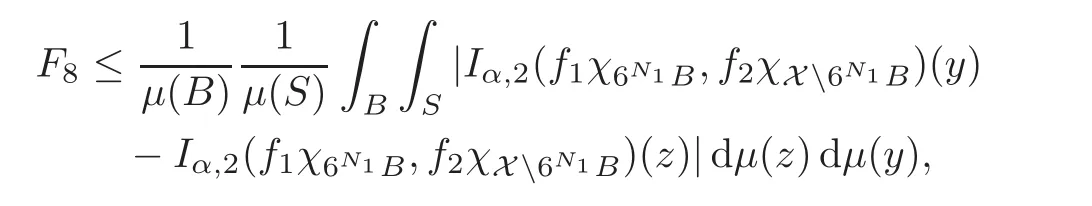
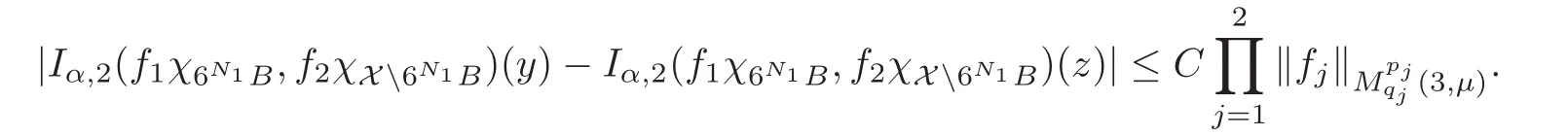
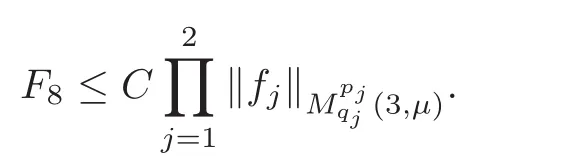
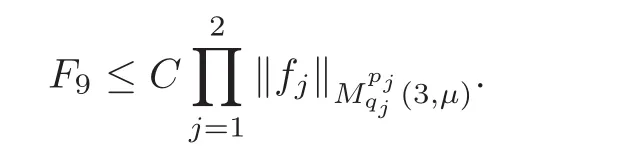
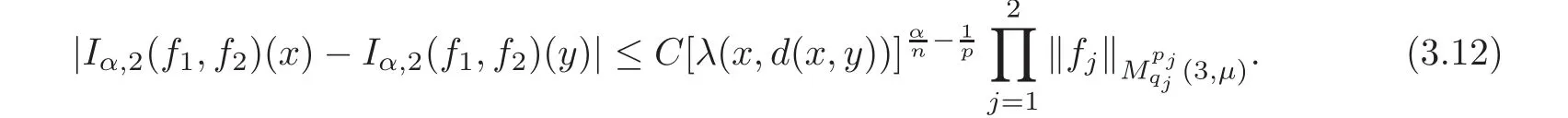
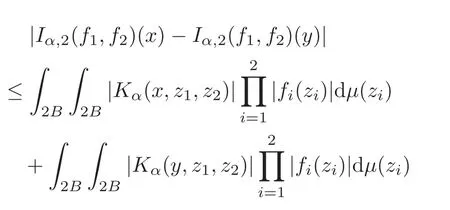
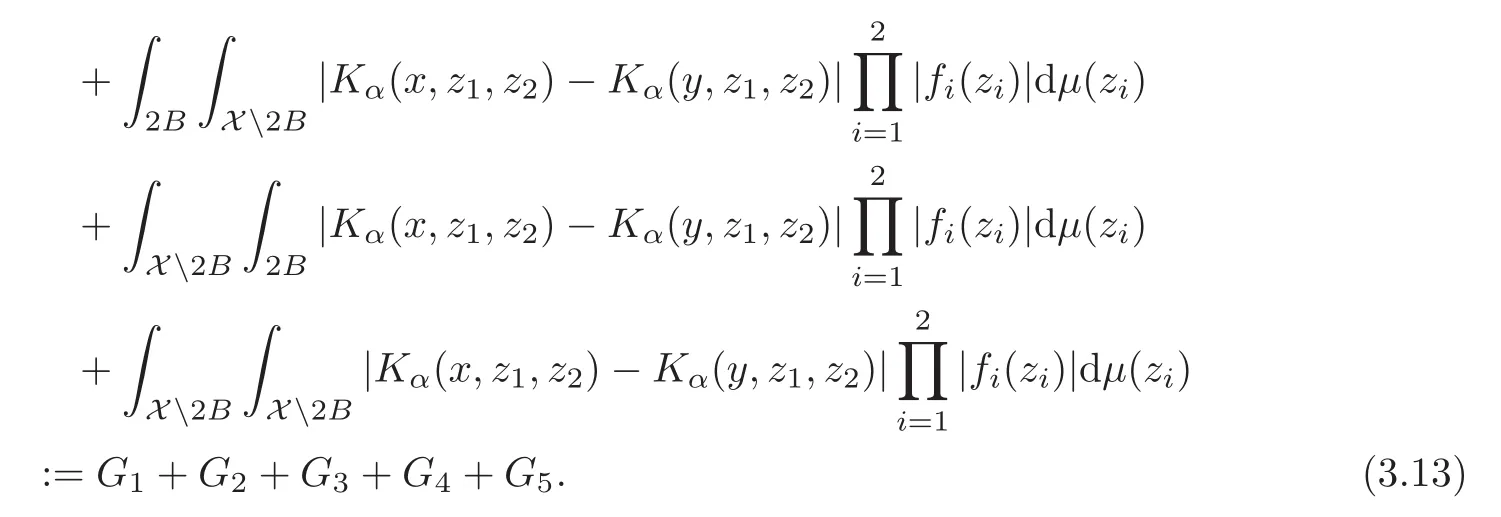

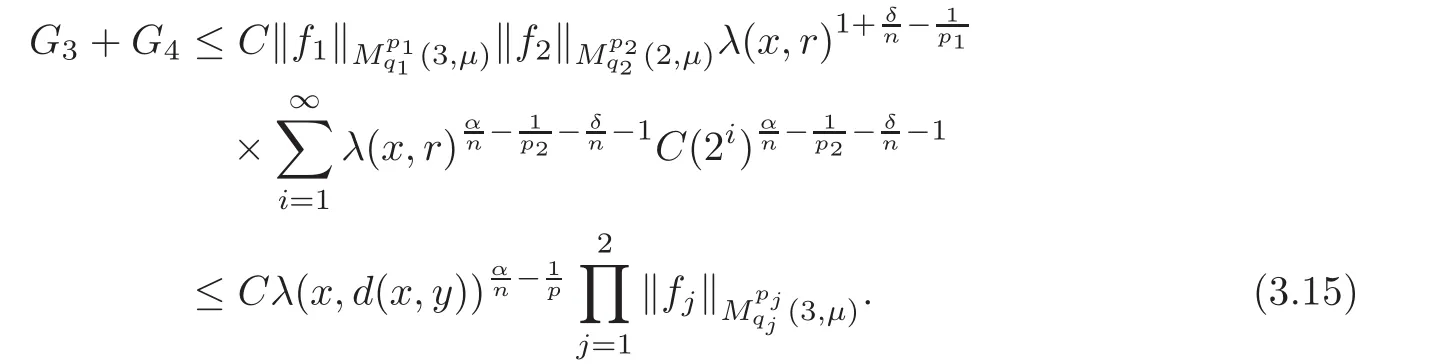
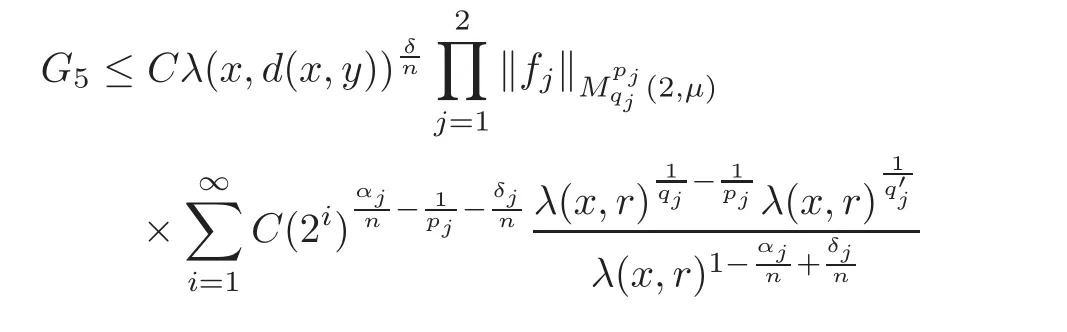

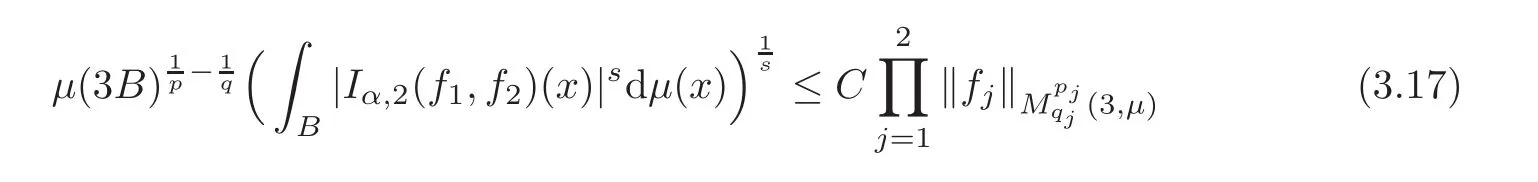


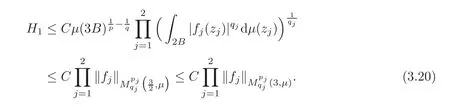
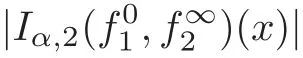
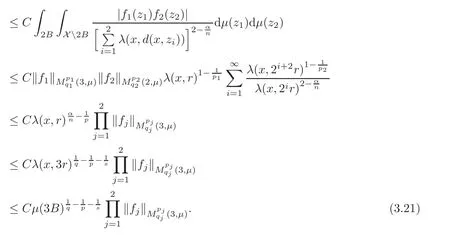


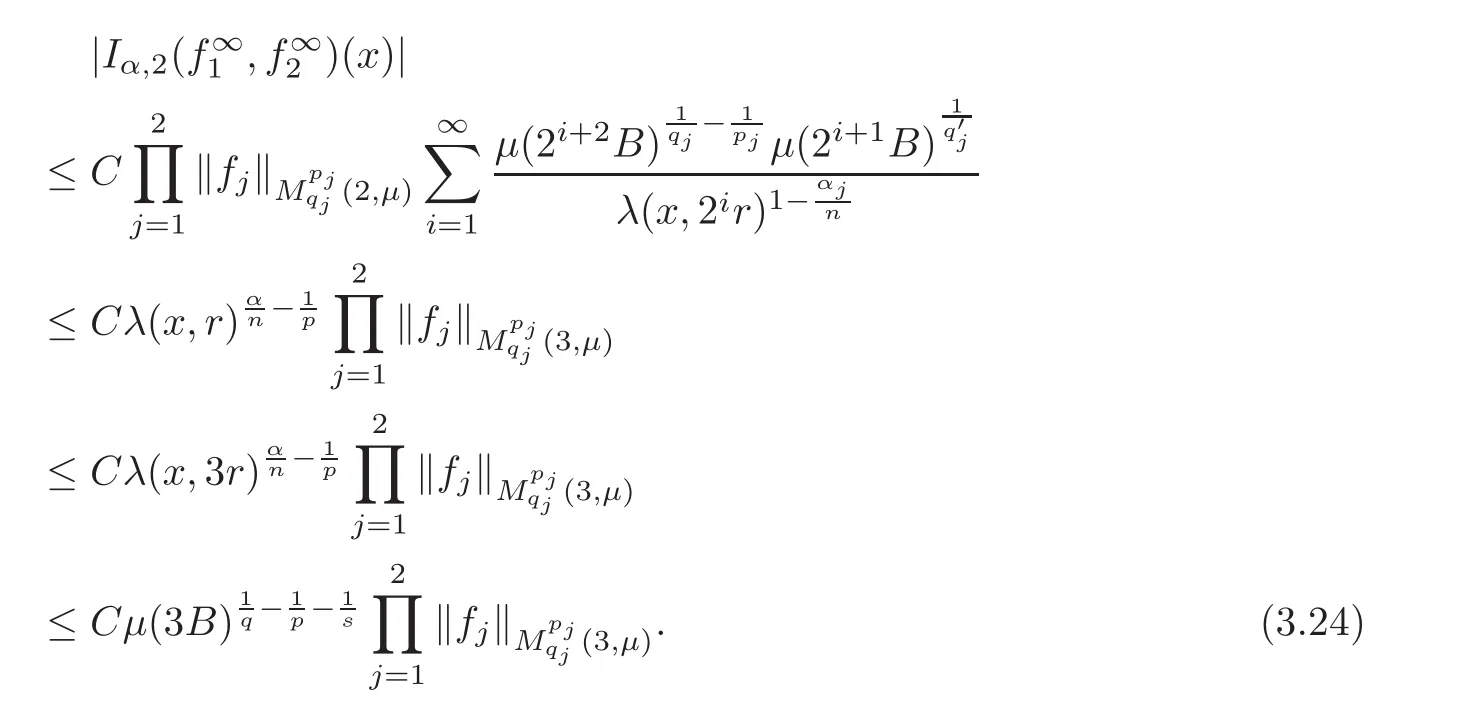

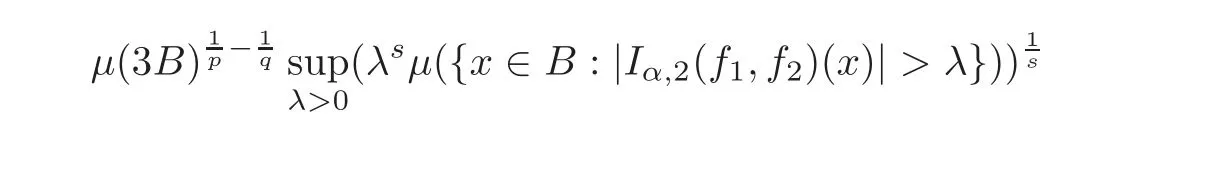
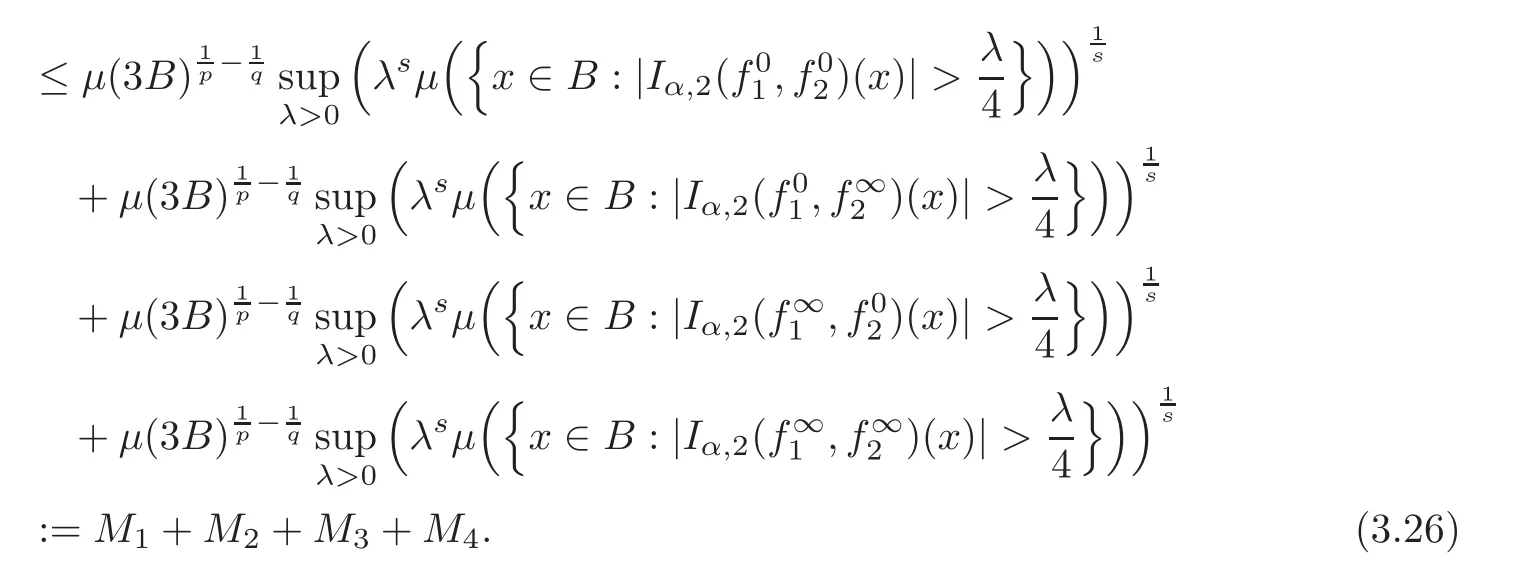



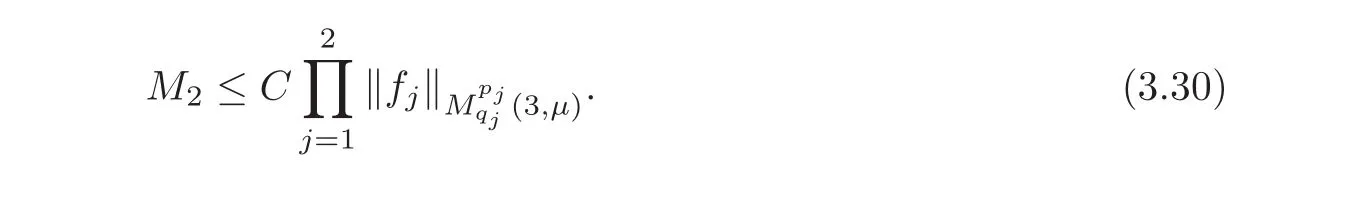
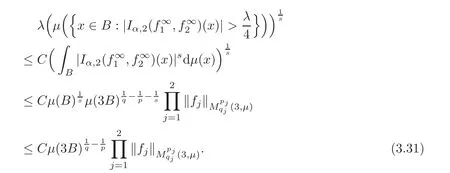
 Chinese Annals of Mathematics,Series B2018年4期
Chinese Annals of Mathematics,Series B2018年4期
