On Affine Connections Induced on the(1,1)-Tensor Bundle

Murat ALTUNBAS Aydin GEZER

Abstract Let M be an n-dimensional differentiable manifold with an affine connection without torsion and (M)its(1,1)-tensor bundle.In this paper,the authors define a new affine connection on (M)called the intermediate lift connection,which lies somewhere between the complete lift connection and horizontal lift connection.Properties of this intermediate lift connection are studied.Finally,they consider an affine connection induced from this intermediate lift connection on a cross-section σξ(M)of T11(M)defined by a(1,1)-tensor field ξ and present some of its properties.

Keywords Connections,Geodesic,Semi-symmetry type condition,Sasaki metric,Tensor bundle

1 Introduction

Let M be a differentiable manifold and(M)be its(1,1)-tensor bundle.Given an affine connection∇on M,(M)can be viewed as an almost product manifold.Affine connections on almost product manifolds have been studied the various aspects by several authors.Walker[6]presented the conditions for the existence of a torsion-free affine connection with respect to which the complementary distributions H and V are relatively parallel and path parallel.Yano[7]reformulated these conditions in terms of local coordinates with respect to adapted frame.Davies[1]defined this connection on the tangent bundle of M and showed how certain special connections lead to some simple expressions for the curvature tensor of the tangent bundle.Later,Mok[3]considered this connection on the cotangent bundle of M and called it as intermediate lift of the connection∇.In this paper,we construct the intermediate lift connection on(M),the construction being the analogue of the connection on the tangent bundle that was considered by Davies[1].We have computed the components of the curvature tensors of the intermediate and horizontal lift connections on(M)with respect to adapted frame and investigate their curvature conditions of semi-symmetry type and Ricci semi-symmetry type.Finally,we present some properties concerning an affine connection induced from the intermediate lift connection on the cross-section σξ(M)of(M)defined by a(1,1)-tensor field ξ with respect to the adapted(B,C)-frame.

We assume in the sequel that the manifolds,functions,tensor fields and connections under consideration are all of differentiability of class C∞.

2 Preliminaries

Throughout,M denotes an n-dimensional C∞-differentiable manifold.Its(1,1)-tensor bundle is denoted by(M)and π :(M)→ M is the projection mapping.Recall that(M)has a structure of(n+n2)-dimensional differentiable manifold induced from the differentiable manifold structure of M.Let(U,xj)be a coordinate neighborhood of M,where(xj)is a system of local coordinates defined in the neighborhood U.Let()be the system of Cartesian coordinates in each(1,1)-tensor space(M)of M at P with respect to the natural frame

where P is an arbitrary point belonging to U.Then,in π−1(U)of T11(M),we can introduce the local coordinates(π−1(U),xj,),which are called the induced coordinates.From now on,we denote the induced coordinates byWe also denote the natural frame in π−1(U)by

and

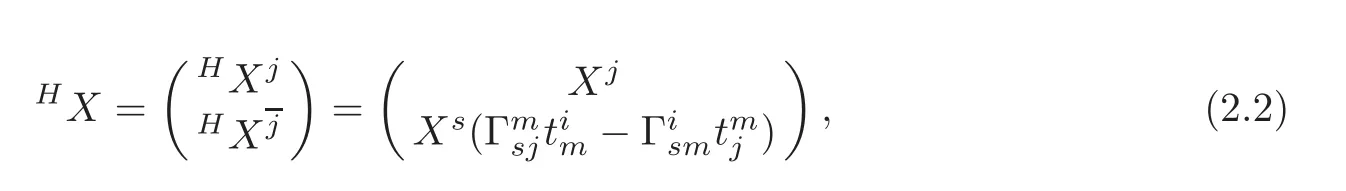
Put X(j)= ∂j=in(2.1)andin(2.2).Then we get in each induced coordinate neighborhood π−1(U)of T11(M)a frame field which consists of the following n+n2linearly independent vector fields:

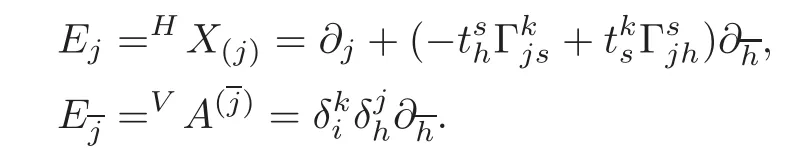
We can write the adapted frame as{Eα}={Ej,Ej}.The indices α,β,γ,···=1,···,n+n2indicate the indices with respect to the adapted frame.

Using(2.1)–(2.2),we obtain

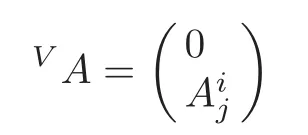
and

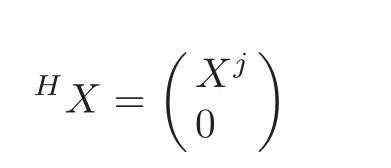
with respect to the adapted frame{Eα}(for details,see[4]).By the routine calculations,we state the lemma below.

Lemma 2.1 The Lie brackets of the adapted frame of T11(M)satisfy the following identities:

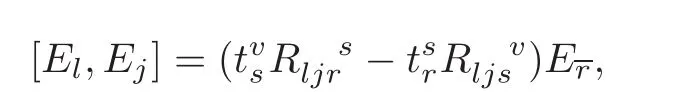
3 T11(M)as an Almost Product Manifold

The vertical distribution V is given by the fibres and the horizontal distribution H is determined uniquely by∇as complementary distribution to V on the(1,1)-tensor bundle(M)of M.The pair(H,V)defines an almost product structure on(M),i.e.,(M)becomes an almost product manifold.

The(1,1)-type projection tensors of(M)onto H and V will again be denoted by H and V.Also,they satisfy the following conditions:

where I is the identity tensor.

When we have an affine connectione∇on an almost product manifold,we can investigate some parallelism conditions of the distributions of the almost product manifolds.These conditions are locally presented in[7].On T11(M),these conditions are in the following forms:

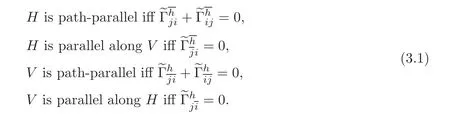
In[1],Davies considered two special tensor fields marked by A and B on a tangent bundle of a manifold M.Now,by following the same method employed by Davies,we shall define the two special tensor fields on T11(M).For all vector fieldseX andeY on T11(M),the A-tensor field is achieved from two configuration tensor fields such that

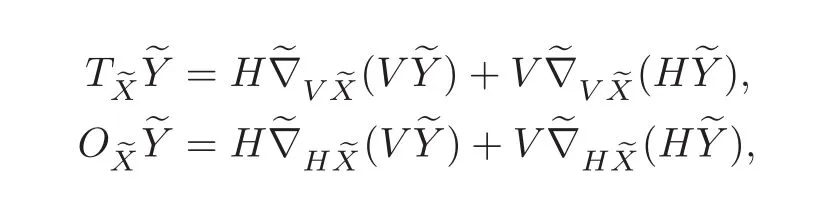
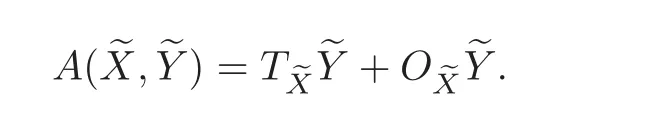
The B-tensor field is coming out with using the A-tensor field as 2BThe A-tensor and B-tensor fields are both the(1,2)-type tensor fields on T11(M)and locally expressed in the following forms:

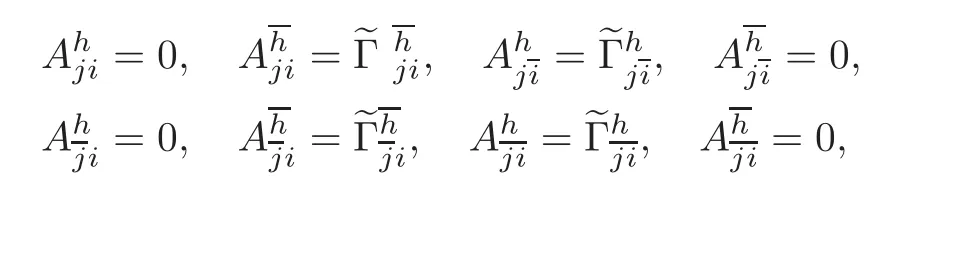
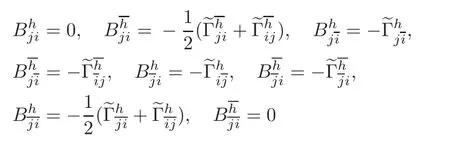
with respect to the adapted frame{Eα}.

4 Lifts of a Torsion-Free Affine Connection to T11(M)

The horizontal liftH∇of any torsion-free connection∇on M is defined by

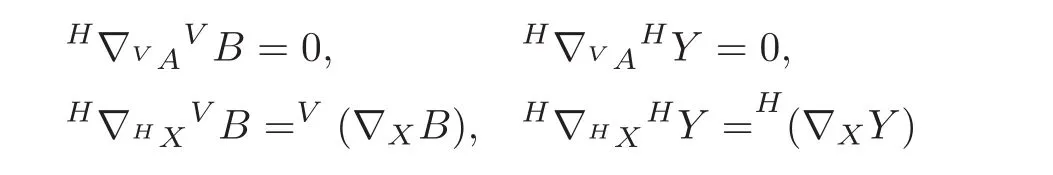
for any vector fields X and Y and(1,1)-tensor fields A and B on M.The non-zero componentsof the horizontal lift connectionH∇ are as follows:

with respect to the adapted frame{Eα}(see[2,4],for(p,q)-tensor bundles,see[5]).

The complete liftC∇of any torsion-free connection∇on T11(M)is given by

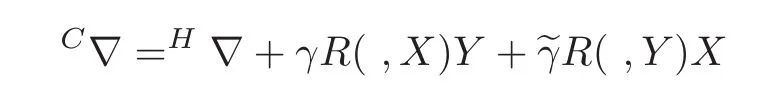
for vector fields X and Y on M,where R is the curvature tensor field of∇and

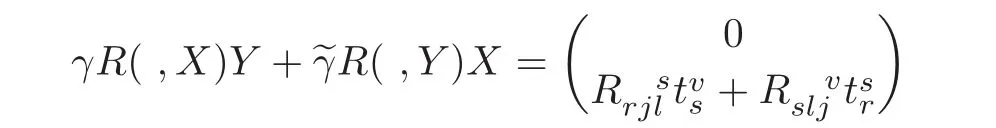
with respect to the adapted frame(see[5]).With the help of(4.1),we find the non-zero coefficients of the complete lift connectionC∇with respect to the adapted frame as follows:

When these components are compared with the conditions in(3.1),it can be seen that V is path parallel and is parallel along H,and H is parallel along V but H is not path parallel.

We are going to define the intermediate liftI∇ of any torsion-free connection∇.To do this,we need the B-tensor field associated with the complete lift connectionC∇.The non-zero component of B is only

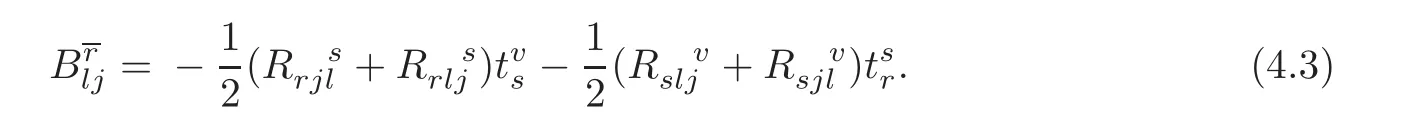
The intermediate liftI∇ of∇ is defined by

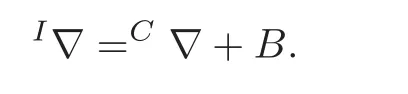
Using(4.2)–(4.3),we obtain

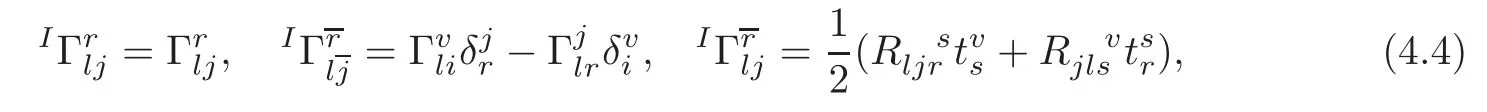
Proposition 4.1 Let M be a differentiable manifold with torsion-free affine connection∇and(M)be its tensor bundle with the intermediate lift connectionI∇.Then,with respect toI∇,

(i)H is parallel along V,

(ii)V is parallel along H,

(iii)H and V are path-parallel in(M).

Since the skew-symmetric part of B of the complete lift connectionC∇is zero,the intermediate lift connectionI∇ is a torsion-free connection.The horizontal lift connectionH∇ can be obtained fromI∇,by using the formula

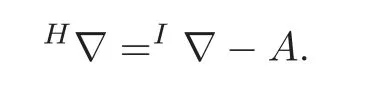
In fact,the non-zero component of A-tensor field associated with the complete lift connectionC∇is

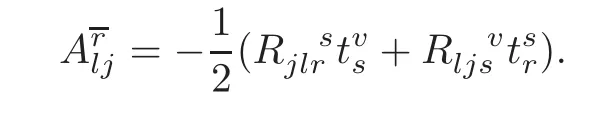
The affine connectionI∇−A has components as non-zero:But these are the same as(4.1),i.e.,I∇−A=H∇.In view of the definition of the intermediate lift connectionI∇,we can say thatI∇ is somewhere between the horizontal lift connectionH∇and the complete lift connectionC∇,so it can be named as“intermediate lift”.

We would like to remind Sasaki metricSg on(M)to show under which conditions the horizontal,complete lift and intermediate lift connections are metrical with respect toSg.For detailed interpretation ofSg,see[4].The Sasaki metricSg on the(1,1)-tensor bundle(M)over a Riemannian manifold(M,g)has the components with respect to the adapted frame{Eα}(see[2,4]):

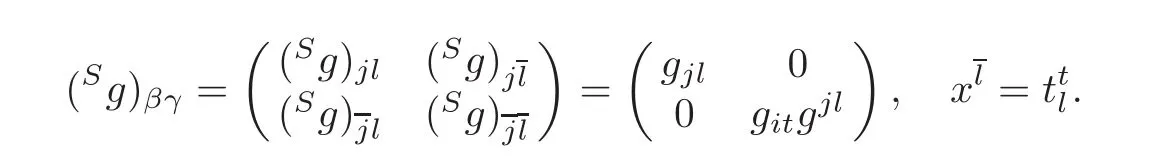
Calculating the covariant derivatives ofSg with respect to the horizontal,complete and intermediate lift connections,we get respectively their non-zero components as follows:

From the equations above,we get the following proposition.

Proposition 4.2 Let(M,g)be a Riemannian manifold with the torsion-free affine connection∇and(T11(M),Sg)be its tensor bundle with Sasaki metric.Then the following conditions are equivalent:

(i)∇is the Levi-Civita connection of g and is locally fl at.

(ii)The complete lift connectionC∇is metrical with respect toSg.

(iii)The intermediate lift connectionI∇is metrical with respect toSg.

In this case,C∇ =I∇ =H∇ and it is the Levi-Civita connection ofSg.

An important geometric problem is to find the geodesics on the smooth manifolds with respect to the affine connections.Let C be a curve in M expressed locally by xr=xr(t).We define a curveeC in T11(M)by

The geodesics of any connectionis given by the differential equations

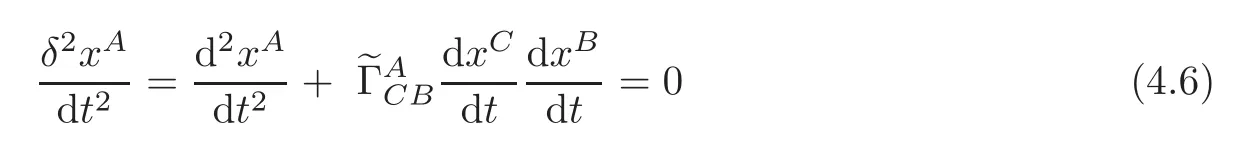
with respect to the induced coordinates(xr,xr),where t is the arc length of a curve in(M).We write down the form equivalent to(4.6),namely,

with respect to the adapted frame{Eα},where

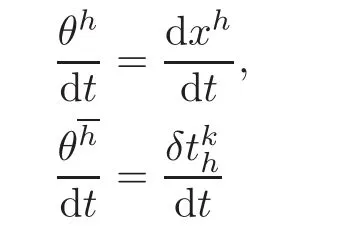
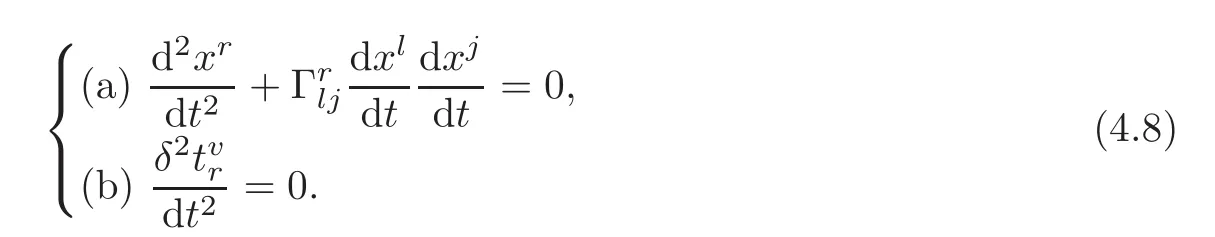
Thus we have the following result.

Theorem 4.1 LeteC be a curve in(M)locally expressed by xr=xr(t),=(t)with respect to the induced coordinates(xr,)in π−1(U)⊂(M).The curveis a geodesic with respect to the intermediate lift connectionI∇if the projection C ofis a geodesic in M with the torsion-free connection∇and(t)satisfies the differential equation(b)in(4.8).

The curvature tensor of the intermediate lift connectionI∇is denoted byIR:

with respect to the adapted frame.Its non-zero components in the adapted frame are found to be

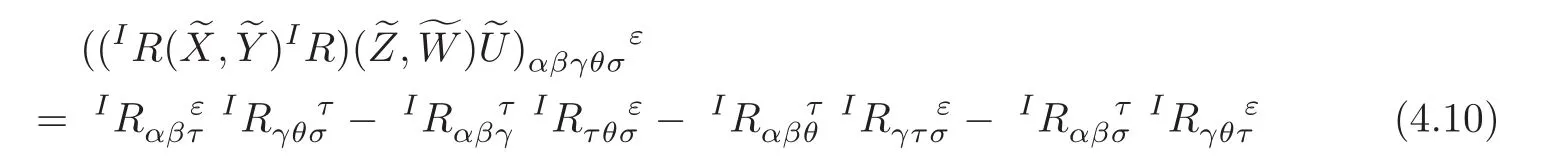
with respect to the adapted frame{Eα}.Similarly,for all Z,W and U on M,

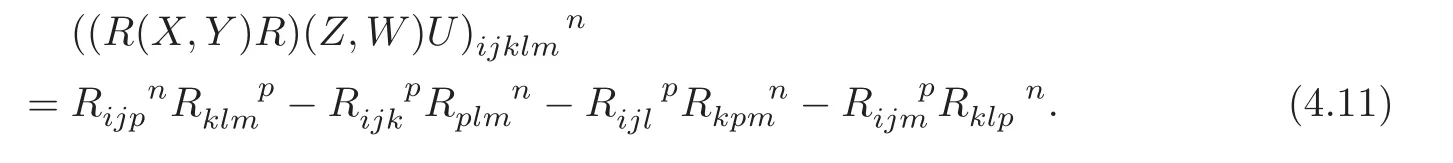
As is known,if the Riemannian curvature tensor of a Riemannian manifold satisfies the condition(4.11),then the Riemannian manifold is called a semi-symmetric manifold.

Using(4.9)–(4.10),computing the coefficients offor different indices,we get

The above conditions give the following theorem.

Theorem 4.2 Let M be a differentiable manifold with torsion-free affine connection∇and(M)be its tensor bundle with the intermediate lift connectionI∇.Under the assumption thatIwhere R andIR are the curvature tensors of the torsion-free affine connection∇and the intermediate lift connectionI∇,if and only if(R(X,Y)R)(Z,W)U=0 for all X,Y,Z,W and U on M.

We obtain the Ricci tensor ofIR by using the well known contractionThe non-zero component ofIRβγis obtained as

Now,we operate the curvature operatorto the Ricci tensor.The tensorsand(R(X,Y)Ric)(Z,W)have coefficients

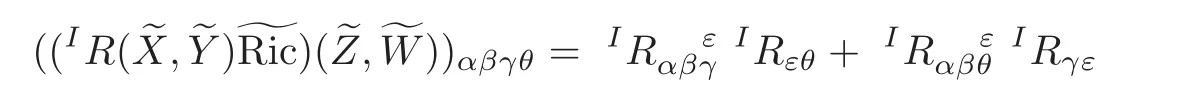
and

respectively.By putting α =m,β =l,γ =j,θ=r,it follows that

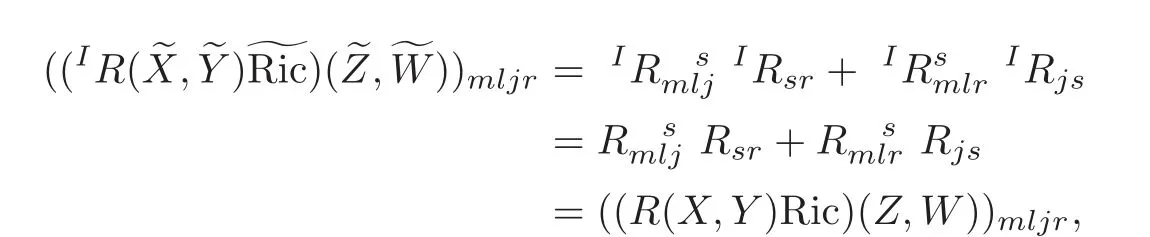
all the others being zero.Therefore we get the following theorem.

Theorem 4.3 Let M be a differentiable manifold with torsion-free affine connection∇and(M)be its tensor bundle with the intermediate lift connectionI∇.Thenif and only if(R(X,Y)Ric)(Z,W)=0 for all X,Y,Z and W on M.

The curvature tensor of the horizontal lift connectionH∇has the following non-zero components

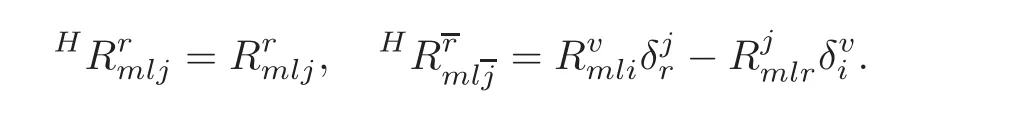
Operating the curvature operatorto the curvature tensorHR,we obtain

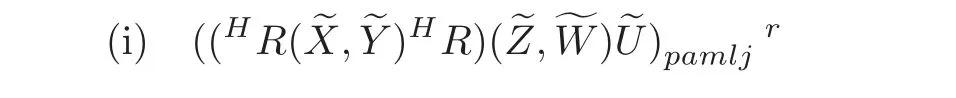
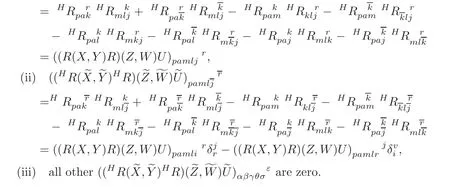
Hence,we have the following result.

Theorem 4.4 Let M be a differentiable manifold with torsion-free affine connection∇andM)be its tensor bundle with the horizontal lift connectionH∇.Thenif and only if(R(X,Y)R)(Z,W)U=0 for all X,Y,Z,W and U on M.

5 The Affine Connection Induced on a Cross-Section from the Intermediate Lift Connection

We shall first find the components of the intermediate lift connectionI∇with respect to the natural frame inbe components of the intermediate lift connectionI∇with respect to the natural frame.The law of transformation of the intermediate lift connectionI∇is as follows:

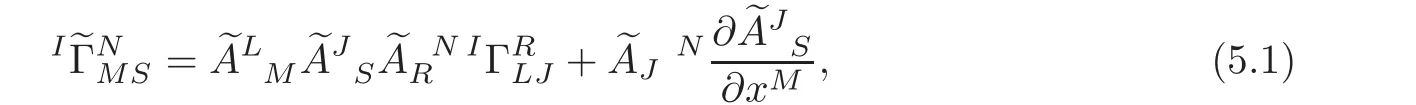
where

is the inverse of the matrix

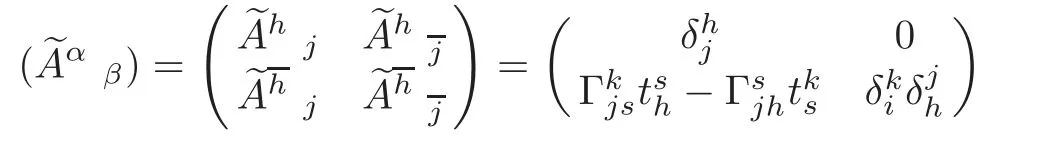
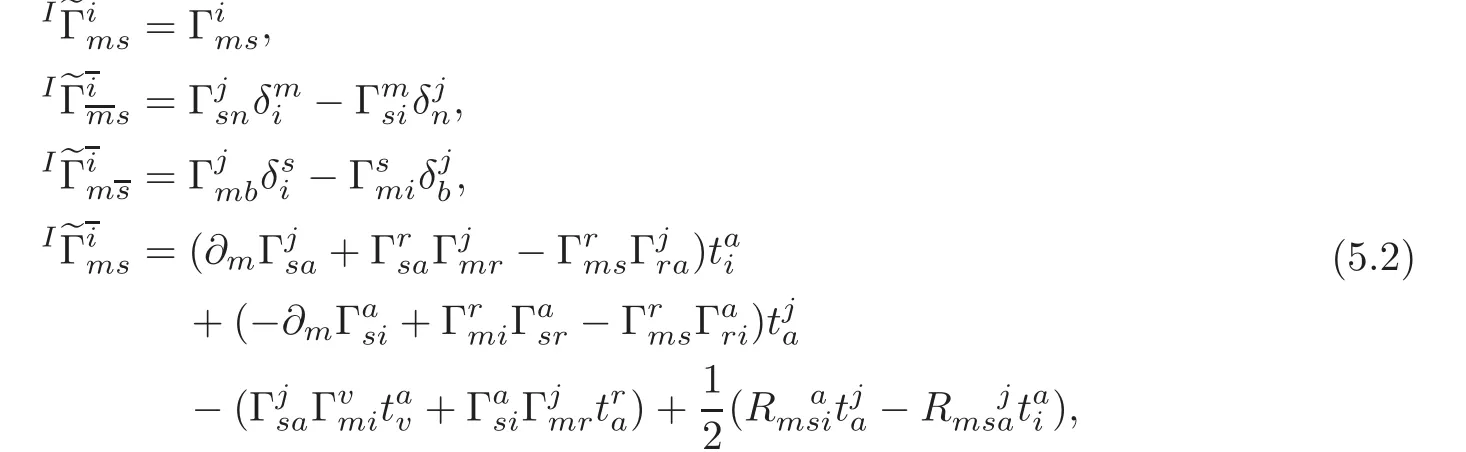
Given a(1,1)-tensor field ξ on M,the correspondence xξx, ξxbeing the value of ξ at x ∈ M,determines a mapping σξ:M(M),such that π ◦ σξ=idM,and the n-dimensional submanifold σξ(M)of(M)is called the cross-section determined by ξ.The cross-section σξ(M)is locally expressed by

On the other hand,the fibre is locally expressed by

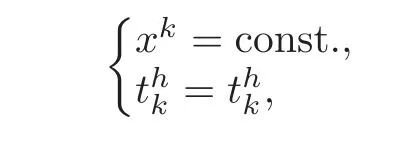
The n+n2local vectors{Bj,Cj}define a local family of frames along σξ(M),which is called the adapted(B,C)-frame of σξ(M).

We now investigate an affine connection induced from the intermediate lift connectionI∇on the cross-section σξ(M)with respect to the adapted(B,C)-frame.The vector fields Cjgiven by(5.5)are linearly independent and not tangent to σξ(M).Here,we take the vector fie lds Cjas normals to the cross-section σξ(M).The componentsof the affine connection induced on σξ(M)from the intermediate lift connectionI∇are in the following form:

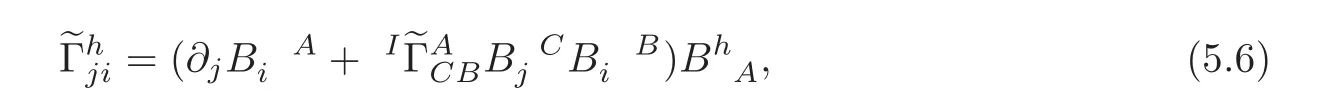
where BhAare defined by

and hence

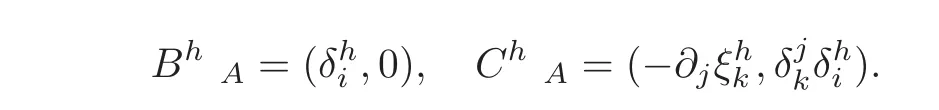
Substitution(5.2)into(5.6)gives

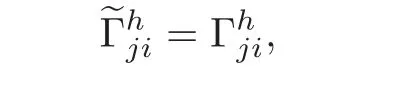
From(5.6)we have

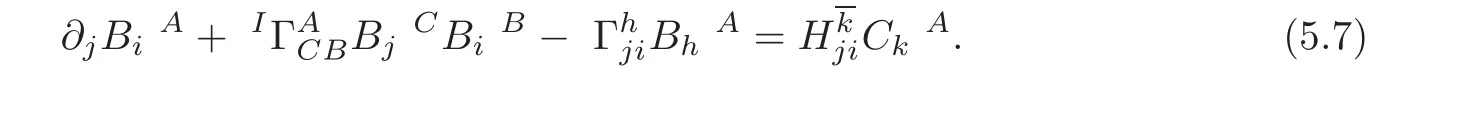
which is the Gauss equation for the cross section σξ(M).Hence,we have the following proposition.

Proposition 5.1 Let σξ(M)be a cross-section in(M)determined by a(1,1)-tensor field ξ on M with torsion-free affine connection ∇.Then,the cross-section σξ(M)is totally geodesic if and only if the condition

is fulfilled.

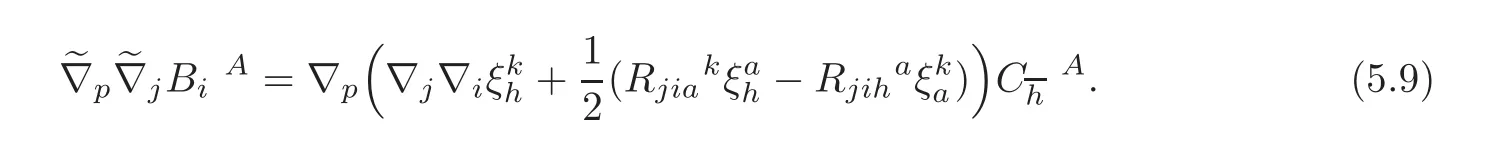
Using

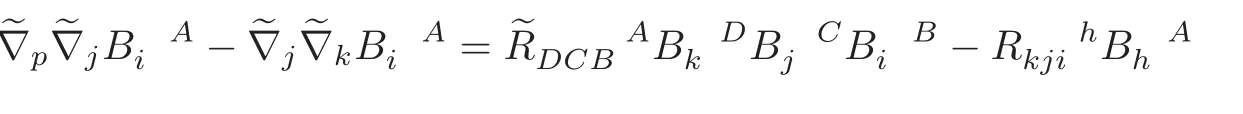
and the Ricci identity for(1,1)-type tensor,it follows from(5.9)that

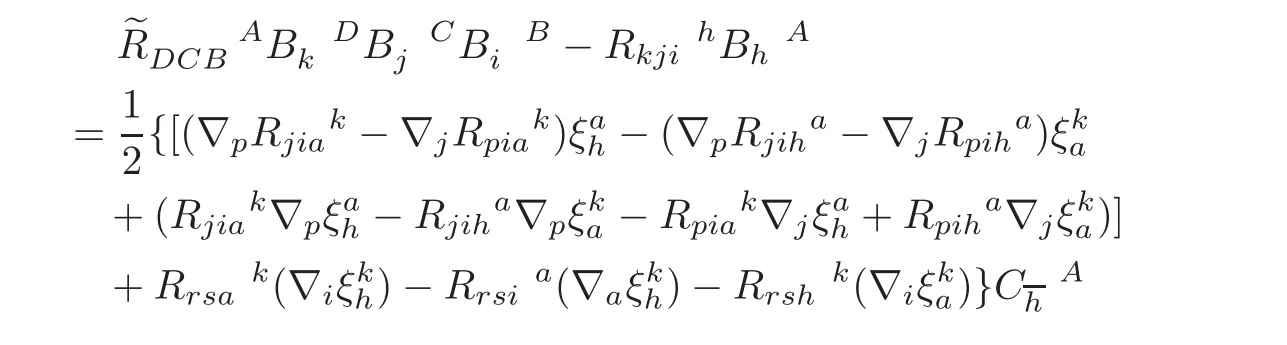
from which we have the following proposition.

is fulfilled.