On Bounded Positive(m,p)-Circle Domains∗
Hongjun LIChunhui QIUYichao XU
AbstractLet D be a bounded positive(m,p)-circle domain in C2.The authors prove that if dim(Iso(D)0)=2,then D is holomorphically equivalent to a Reinhardt domain;if dim(Iso(D)0)=4,then D is holomorphically equivalent to the unit ball in C2.Moreover,the authors prove the Thullen’s classification on bounded Reinhardt domains in C2by the Lie group technique.
Keywords(m,p)-Circular domain,Reinhardt domain,Holomorphically equivalent
1 Introduction
Let D be a bounded domain containing the origin in C2.Denote by Aut(D)the holomorphic automorphism group of the domain D,Aut(D)0the unit connected component of Aut(D),and Iso(D)the isotropic subgroup with the origin of Aut(D)and Iso(D)0the unit connected component of Iso(D).Cartan[1]proved that Aut(D)is a real Lie group and Iso(D)is a compact Lie subgroup of Aut(D).In this paper,L is called the Lie algebra of a Lie group G,if L consists of all left invariant vector fields of the Lie group G.Moreover,aut(D)and iso(D)denote the Lie algebras of the Lie group Aut(D)and Iso(D),respectively.
If Iso(D)0has a 1-dimensional real Lie subgroup
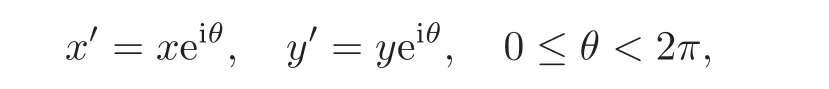
we call D a circle domain;if Iso(D)0has a 2-dimensional real Lie subgroup
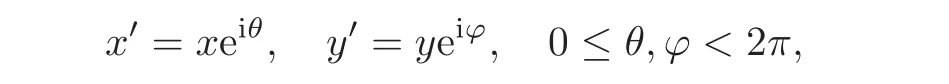
we call D a Reinhardt domain;if Iso(D)0has a 1-dimensional real Lie subgroup
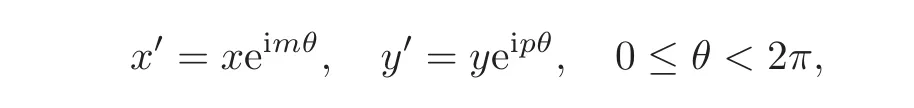
where m,p∈Z,m>p≥1,g.c.d.(m,p)=1,we call D a positive(m,p)-circle domain;if Iso(D)0has a 1-dimensional real Lie subgroup we call D a semi-circle domain.
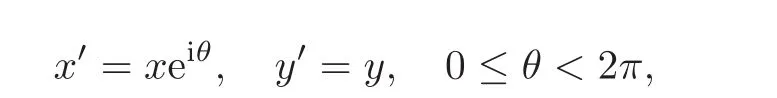
By using the Thullen condition:dim(Aut(D))>dim(Iso(D)),Thullen[2]succeeded in classifying bounded Reinhardt domains in C2.Any bounded Reinhardt domain with the Thullen condition in C2is linearly equivalent to one of the three classes:
(1)Polydisc∆2={(x,y)∈C2:|x|<1,|y|<1};
(2)Thullen domain Dλ={(x,y)∈ C2:|x|2+|y|λ<1}(λ >0,λ 6=2);
(3)Unit ball B2={(x,y)∈C2:|x|2+|y|2<1}.
By adding the condition:Iso(D)0⊂U2,where U2is a unitary group of degree 2,Cartan[3]gave some classification and realization of domains in C2.For circular domains and a part of semi-circular domains in C2,Cartan[4]gave the classification and the realization.
Xu and Wang[5–6]gave the classification and the realization of bounded positive(m,p)-circle domains and bounded semi-circle domains when the isotropic subgroup with the origin is a 1-dimensional real Lie group.The holomorphic automorphism groups are also determined.Clearly,all Reinhardt domains in C2are semi-circle domains and positive(m,p)-circle domains.
Recently,Yamamori[7]proved that the isotropic subgroup with the origin of bounded positive(m,p)-circle domains is a linear group when p≥2.Yamamori[8]and Rong[9]also obtained some more general results in Cn.
In this paper,we only consider bounded domains containing the origin with the Thullen condition:dim(Aut(D))>dim(Iso(D)).
2 The Isotropic Subgroup of Bounded Positive(m,p)-Circle Domains
In this section,we consider a bounded positive(m,p)-circle domain D with dim(Iso(D)0)=2 or 4.By the definition,if D is a bounded positive(m,p)-circle domain,then
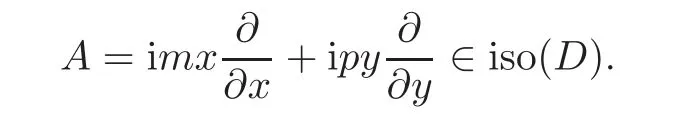
Firstly,we introduce some results of Cartan.
Lemma 2.1(cf.[1])Let D be a bounded domain in Cn.If the Taylor expansions at z=0 of σ,τ∈ Iso(D)are
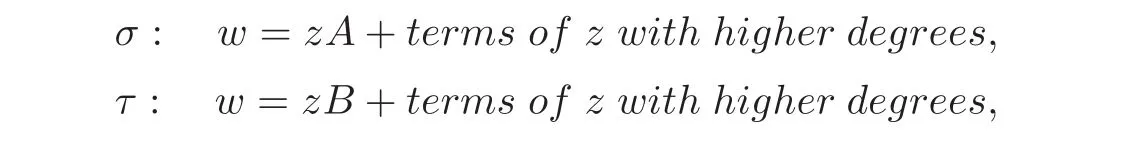
respectively,then σ=τ if and only if A=B,where A,B ∈ GL(n,C).
Lemma 2.2(cf.[1])Let D be a bounded domain in Cn.If the Taylor expansions at z=0iso(D)are
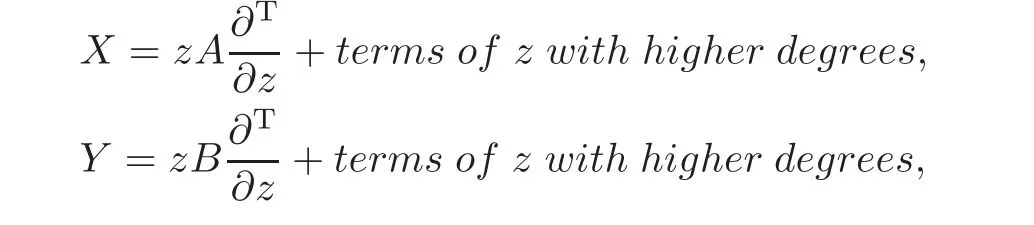
Lemma 2.3(cf.[1]) Let D be a bounded domain in Cn.Given a vector field X=∈aut(D),then X,iX∈aut(D)if and only if X=0.Moreover,X∈iso(D)if and only if ξ(0)=0.
Lemma 2.4(cf.[3])Let D be a bounded positive(m,p)-circle domain,then dim(Iso(D)0)=1,2,4.When dim(Iso(D)0)=2 or 4,there exists a homogeneous complex affine transformation(u,v)=(x,y)Q,Q∈GL(n,C),which maps D onto a bounded domain D1,and Iso(D1)0isterms of(u,v)with higher degrees, 0 ≤ θ,ϕ <2π,or
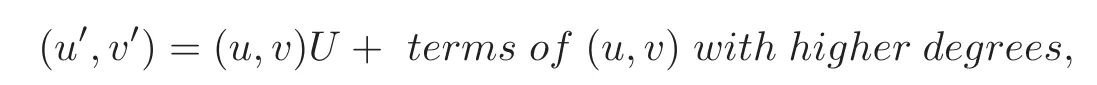
where U is the traversal of all unitary matrices of degree 2.
Now we can get the following theorem.
Theorem 2.1 Suppose that D is a bounded positive(m,p)-circle domain,and Q is defined in Lemma 2.4.If dim(Iso(D)0)=2,then
or
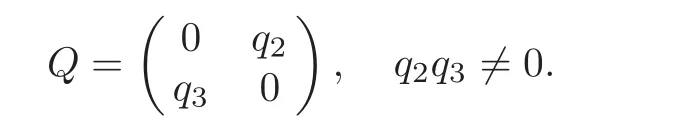
If dim(Iso(D)0)=4,then
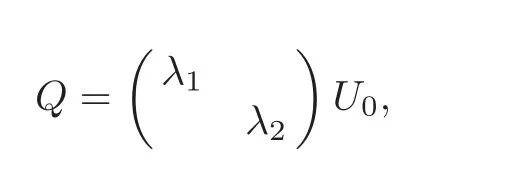
where λ1,λ2>0,U0is a unitary matrix of degree 2.
Proof Since Iso(D)0has a 1-dimensional real Lie subgroup

Iso(D1)0has a 1-dimensional real Lie subgroup
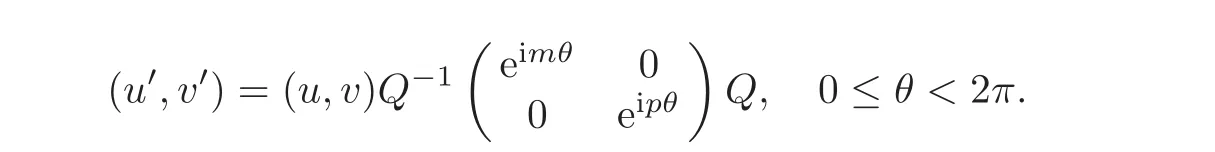
(I)The case of dim(Iso(D)0)=2
Since Iso(D1)0is
(u′,v′)=(u,v)terms of(u,v)with higher degrees, 0 ≤ θ,ϕ <2π,by Lemma 2.1,for any fixed 0≤ θ<2π,there exists a unique matrixsuch that
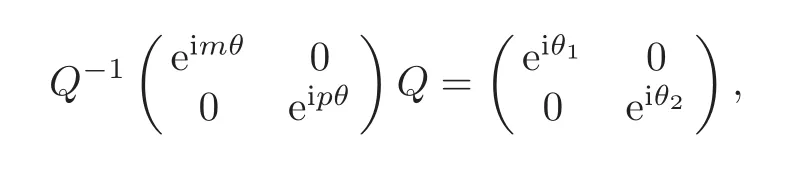
where θ1,θ2are real continuous functions on t∈ R.Denoteso we have

By a direct computation,we can get
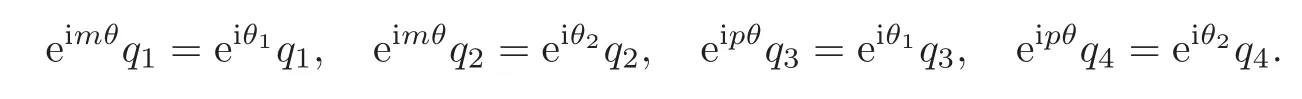
As we know,detQ 6=0,i.e.,q1q4−q2q36=0.
(1)If q4=0,then q2q36=0,i.e.,q26=0 and q36=0.So eimθ=eiθ2,eipθ=eiθ1.If q16=0,then we have eimθ=eiθ1=eipθ.Clearly,eimθ=eipθdoes not hold for any θ ∈ [0,2π).So q1=0.As the same reason,if q1=0,then q4=0.
(2)If q2=0,then q1q46=0,i.e.,q16=0 and q46=0.As the same reason as(1),we can get q2=q3=0.
(3)If q1q26=0,according to(1)and(2),we can get q3q46=0.So eimθ=eipθholds for any θ∈ [0,2π),which gives a contradiction.
(II)The case of dim(Iso(D)0)=4.
Since Iso(D1)0is
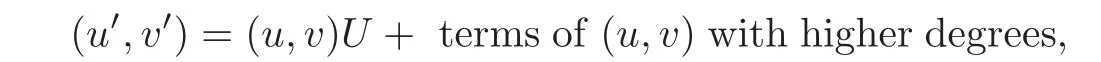
where U is the traversalof all unitary matrices of degree 2,by Lemma 2.1,i.e.,
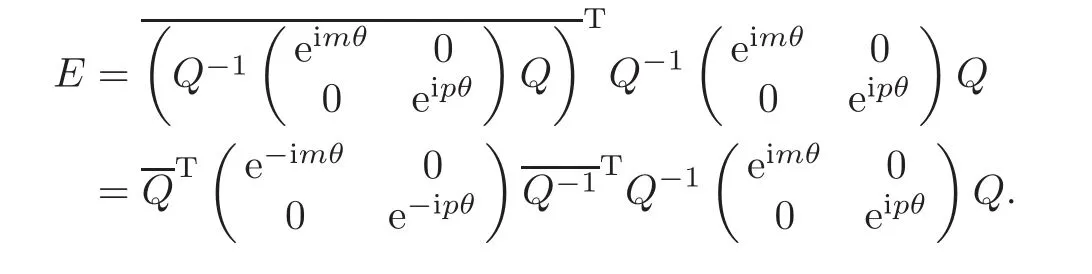
By a direct computation,we have
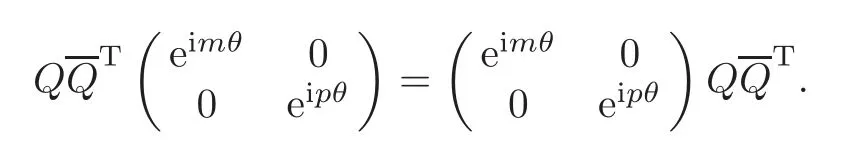
Note that for a bounded positive(m,p)-circle domain D,if dim(Iso(D)0)=2,then Iso(D1)0has a 1-dimensional real Lie subgroup
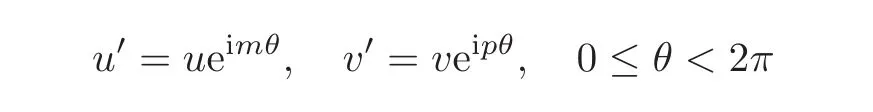
or
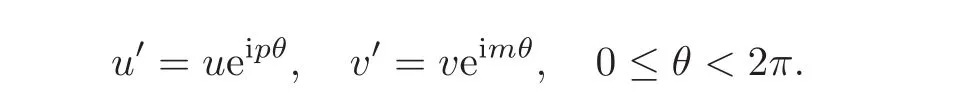
In the sense of holomorphic equivalence,we regard the two cases as the same class.If
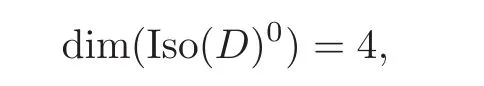
then Iso(D)0is
(x′,y′)=(x,y)QUQ−1+terms of(x,y)with higher degrees
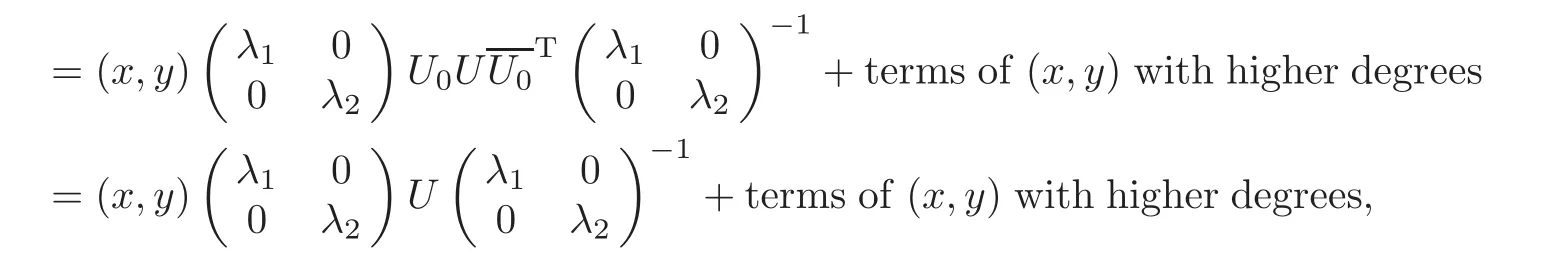
where U is the traversal of all unitary matrices of degree 2.Set κ :Then D2=κ(D)is a bounded positive(m,p)-circle domain,and Iso(D2)0is
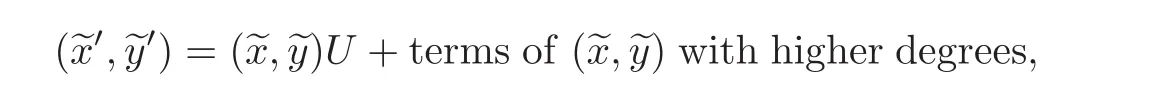
where U is the traversal of all unitary matrices of degree 2.Without loss of generality,for a bounded positive(m,p)-circle domain D,suppose that the Taylor expansion at z=0 of any σ∈Iso(D)0is

where U is a unitary matrices of degree 2.
Now we can get the following lemmas.
Lemma 2.5 Let D be a bounded positive(m,p)-circle domain with dim(Iso(D)0)=2.If p>1,then D is a Reinhardt domain;if p=1,then D is holomorphically equivalent to a Reinhardt domain.
Proof Suppose that the Lie algebra iso(D)has a group of basesand
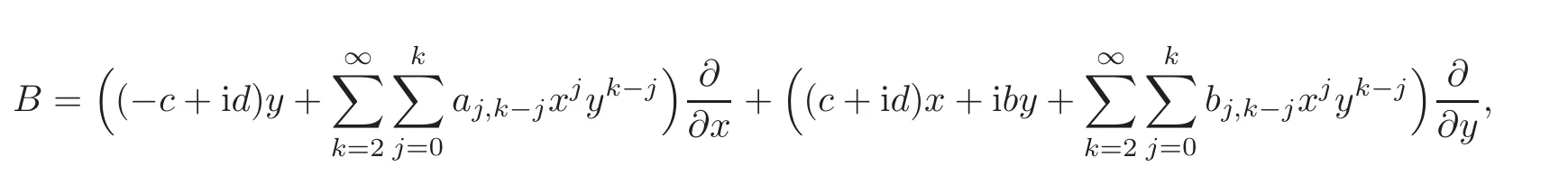
where 0 6=(b,c,d)∈ R3,aj,k−j,bj,k−j∈ C,k ≥ 2,0≤ j≤ k.Since[A,B]∈ iso(D),there are λ,µ ∈ R,such that[A,B]= λA+µB.
Firstly,we want to prove that λ = µ =0.In fact,
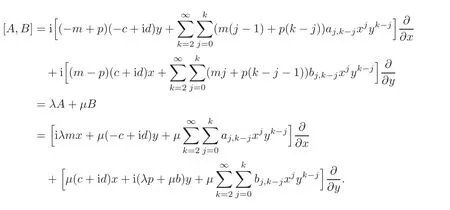
It follows that
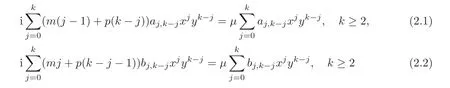
and
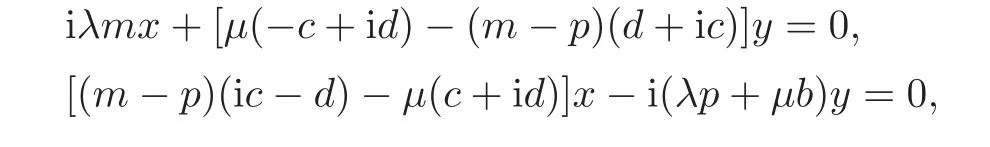
hence λ =0,µb=0,(m−p)c= µd,(m−p)d= −µc.
Supposing thatµ 6=0,we have d(m − p)= −cµ and c(m − p)=dµ.Hence−cdµ =d2(m−p)=−c2(m−p).When m 6=p,then c2+d2=0,hence c=d=0.Byµb=0,we have b=0.But(b,c,d)6=0,it gives a contradiction.
Suppose that λ= µ =0,hence[A,B]=0,c=d=0,b 6=0.
When p>1,from(2.1)–(2.2),we haveSo the Lie algebra iso(D)has a group of bases ixand D is a Reinhardt domain.
When p=1,from(2.1)–(2.2),we have ajk=bjk=0,j+k ≥ 2,but we do not know a0m,So the Lie algebra iso(D)has a group of bases A,B,where
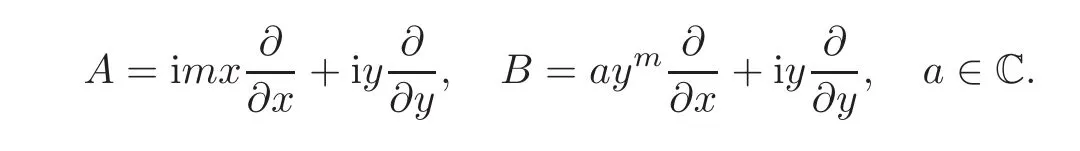
The one-parameter subgroup exp(tB)(t∈R)is a unique holomorphic solution of the complex ordinary differential equation systems
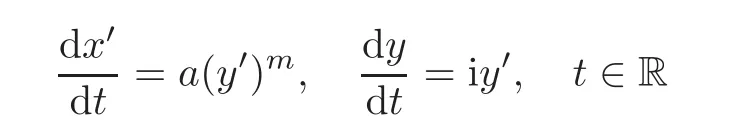
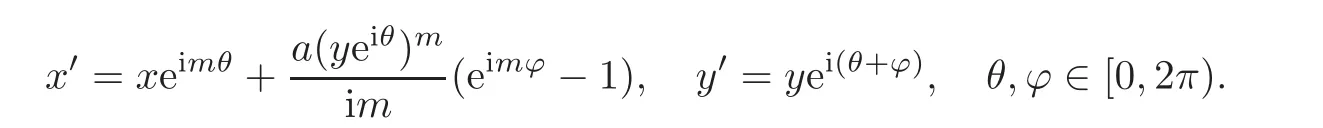
Given a holomorphic isomorphismthen

Therefore,iso(σ(D))has a group of basesand σ(D)is a Renhardt domain.
Lemma 2.6 Let D be a bounded positive(m,p)-circle domain with dim(Iso(D)0)=4.Then D is holomorphically equivalent to the unit ball in C2.
Proof Since Iso(D)0is

where U is the traversal of all unitary matrices of degree 2,Iso(D)0is isomorphic to U2.By the knowledge of Lie group,Iso(D)0has a 2-dimensional Lie subgroup H which consists of the elements

By Lemma 2.5,the Lie algebra of H has a group of bases ix(in the sense of holomorphic isomorphism).Cartan[3]proved that for any bounded circle domain,its isotropic subgroup is constructed by the linear transformation,so Iso(D)0is

Hence D is holomorphically equivalent to the unit ball in C2.
It is known that dim(Iso(∆2)0)=dim(Iso(Dλ)0)=2,dim(Iso(B2)0)=4.By the Thullen’s classification of Reinhardt domains in C2and Lemmas 2.5–2.6,we immediately obtain the following result.
Theorem 2.2 Let D be a bounded positive(m,p)-circle domain.If dim(Iso(D)0)=2,then D is holomorphically equivalent to a Reinhardt domain which is one of the two classes:
(1)Polydisc∆2={(x,y)∈C2:|x|<1,|y|<1};
(2)Thullen domain Dλ={(x,y)∈ C2:|x|2+|y|λ<1}(λ >0,λ 6=2).If dim(Iso(D)0)=4,then D is holomorphically equivalent to the unit ball

In the next section,we use a new approach to prove Theorem 2.2.By the results of Xu[5],the classification of bounded positive(m,p)-circle domains in the sense of holomorphic isomorphism is given.
3 The Classification of Reinhardt Domains
In the above section,we prove that for a bounded positive(m,p)-circle domain D,if dim(Iso(D)0)=2,then D is holomorphically equivalent to a Reinhardt domain;if dim(Iso(D)0)=4,then D is holomorphically equivalent to the unit ball in C2.Thus in order to classify bounded positive(m,p)-circle domains with the isotropic subgroup of dimensions 2 or 4,we just do the classification of bounded Reinhardt domains in C2.Thullen[3]gave the classification of bounded Reinhardt domains in C2by the geometric property of domains.In this section, firstly we give the Lie algebra of holomorphic automorphism group and holomorphic automorphism group,then prove the Thullen’s classification result again by another method.
In a way similar to[5],we assert that bounded positive(m,p)-circle domains allow holomorphic automorphism families

where α ∈ C.The function g(x,y,α,α)is continuous on(x,y) ∈ D,|α|<1.Then the point set
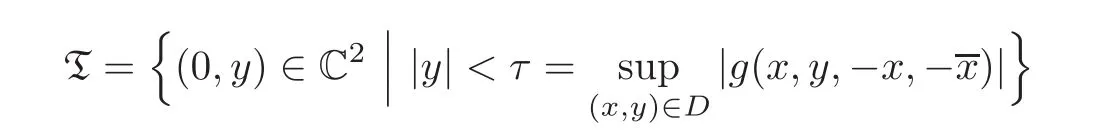
is in D.In fact,the point set
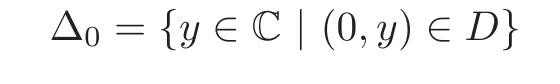
is a bounded open subset in the y-plane.Since eiθ∆0⊂ ∆0,∀θ∈ [0,2π),the point set∆0is constructed by some concentric real circle disks.We consider the sectional set of∆0by the positive axis,the section set is a sequence of open intervals
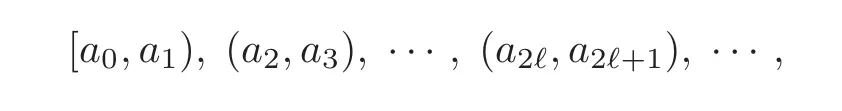
where
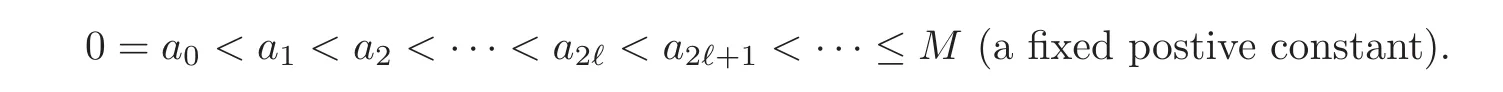
If(x1,y1)∈ D,then φ(x1,y1)=(0,g(x1,y1,−x1,−))∈ D,where
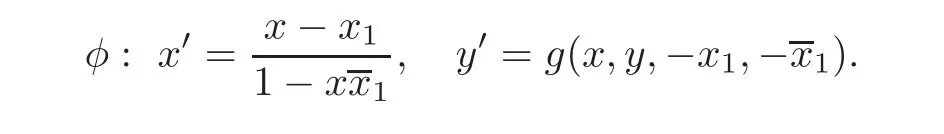
It yields g(x1,y1,−x1,−x1)∈ ∆0.If|g(x1,y1,−x1,−x1)|6=0,then there is an index k,such that
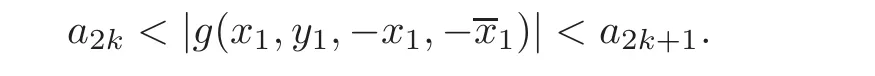
Let

ℓ=0,1,2,···.Then
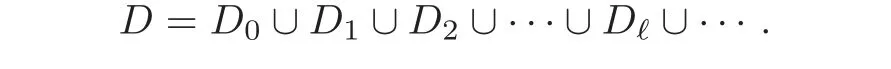
When j Thus In other words,{(0,y)∈C2||y| In order to express bounded positive(m,p)-circle domains by the function g,we introduce a point set Clearly,D consists of bounded positive(m,p)-circle domains.Whereas,we have the following lemma. Lemma 3.1 Suppose that D is a bounded positive(m,p)-circle domain,for any(x1,y1)∈D,satisfying Then D is the point set Lemma 3.2 If D is a bounded Reinhardt domain in C2with dim(Iso(D)0)=4,then iso(D)has a group of bases A,B,C,D,whereSince iso(D)is a real linear space,we have Proof If D is a bounded Reinhardt domain in C2,then Suppose By Lemma 2.2,we obtain that[A+B,X]=0,so Hence thus Re(a10)=Re(b01)=0.We denote If a01=0,then∈iso(D).By Lemma 2.3,we get b10=0.For the same reason,if b10=0,then a01=0.Therefore if a010,then b1060;if b1060,then a016=0.Sinceiso(D),without loss of generality,when b106=0,we suppose b10=1,a016=0.By[C,D]=iso(D),we have a01∈R. The one-parameter subgroup(x′(t),y′(t))=exp(tC)(t∈ R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values x′(0)=x,y′(0)=y.If a01>0,then the solution is which transforms(x0,0)toBut D is a bounded domain,it is a contraction.If a01<0,then the solution is Therefore a01<0,denoting a=−a01>0,we get Lemma 3.3 Suppose that D is a bounded Reinhardt domain in C2,aut(D)is a direct sum of two subspaces:one is iso(D),the other is linear combination of some vector fields as follows where ρ1,λ1≥ 0,ρ2, λ2≥ 0. Proof Since D satisfies the Thullen condition,there exists(a00,b00)6=0,such that By and Lemma 2.2,we know therefore Without loss of generality,we suppose then By Lemma 2.2,we get a02=b20=0.So we have Since we know that aut(D)has elements and Note that if a00=0,then X1=Y1=0;if b00=0,then X2=Y2=0.When a0060,denote=a1+ia2,thenthus we can suppose a00=1.For the same reason,when b006=0,we also can suppose b00=1. If a00=1,then we have thus there exist ρ1,ρ2∈ R,such that a20= −ρ1,b11= −ρ2.For the same reason when b00=1,there exist λ1,λ2∈ R,such that b02= −λ1,a11= −λ2. The one-parameter subgroup(x′(t),y′(t))=exp(tX1)(t ∈ R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values x′(0)=x,y′(0)=y.If ρ1=0,then x′(t)=x+t,t∈ R,which contracts that D is a bounded domain.If ρ1<0,then It is a contraction that D is a bounded domain.If ρ1>0,then Since D is a bounded domain,it yields ρ2≥ 0.Therefore,we have proved ρ1>0, ρ2≥ 0.For the same reason,we can prove λ1>0, λ2≥ 0. Now one can prove the following theorems. Theorem 3.1 Let D be a bounded Reinhardt domain in C2.If dim(Iso(D)0)=2,then aut(D)has a group of basesand Case(I) Case(II) Case(III) If dim(Iso(D)0)=4,then aut(D)has a group of bases where a>0,c>0. ProofIf X1=aut(D),wherethen (1)If dim(Iso(D)0)=2,then Iso(D)0is a real Lie group and iso(D)has a group of bases If a00b006=0,then It yields ρ2= λ2=0.Case(I)holds. If(a00,b00)=(1,0),then X16=0,X2=0.The one-parameter subgroup(x′(t),y′(t))=exp(t((cosς)X1+(sinς)Y1))(t∈ R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values x′(0)=x,x′(0)=y,where ς∈ [0,2π).We get the solution If ρ2=0,then so ρ2=0 does not hold. Next we prove ρ16= ρ2.If ρ1= ρ2,then so ρ1= ρ2does not hold.Therefore,Case(II)holds. If(a00,b00)=(0,1),then X1=0,X26=0.As the same reason as the case(a00,b00)=(1,0),we get λ26=0,and λ16= λ2.Therefore,Case(III)holds. (2)If dim(Iso(D)0)=4,then iso(D)has a group of bases If a006=0,then X16=0.By a direct computation we get ρ1= ρ2.Then Thus b000. If b000,then X20.By a direct calculation we get λ1= λ2.Then Thus a006=0. When a00b006=0,then there exists c ∈ R,such that λ2=aρ2=ac.So we have ρ1= ρ2=c>0,λ1= λ2=ac. Therefore,we have proved that aut(D)has a group of bases where a>0,c>0. Theorem 3.2 Suppose that D is a bounded Reinhardt domain in C2.Then there exists a linear isomorphism σ,such that σ(D)is one of the three classes: (1)Polydisc∆2={(x,y)∈C2:|x|<1,|y|<1}; (2)Thullen domain Dλ={(x,y)∈ C2:|x|2+|y|λ<1}(λ >0,λ 6=2); (3)Unit ball B2={(x,y)∈C2:|x|2+|y|2<1}. Proof If dim(Iso(D)0)=2,then iso(D)has a group of bases: For Case(I),given a linear isomorphismthen aut(σ(D))has a group of bases For fixed t1,t2∈R,the one-parameter subgroup is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values u′(0)=u,v′(0)=v,where ς1, ς2∈ [0,2π).We get the one-parameter analytic transformation: Thus D is linearly equivalent to=σ(D),Aut()0is a real Lie group with dim(Aut()0)=6: For Case(II),given a linear isomorphismthen aut(σ(D))has a group of bases The one-parameter subgroup(u′(t),v′(t))=exp(t(cosς+sinς))(t∈R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values u′(0)=u,v′(0)=v,where ς∈ [0,2π).We get the solution where α=eiςtght.Therefore D is linearly isomorphic to=σ(D),and Aut()0is a real Lie group with dim(Aut()0)=4: where θ,ϕ ∈ [0,2π), α ∈ C,|α|<1.By Lemma 3.1,we can obtain For Case(III),given a linear isomorphismthen aut(σ(D))has a group of bases The one-parameter subgroup(u′(t),v′(t))=exp(t(cosςX∗2+sinςY∗2))(t∈R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values u′(0)=u,v′(0)=v,where ς∈ [0,2π).We get the solution where α=eiςtght.Therefore D is linearly isomorphic to=σ(D),and Aut()0is a real Lie group with dim(Aut()0)=4: By Lemma 3.1,we can get We can see for the domain given a linear isomorphism σ :(x,y)−→ (y,x),then D1is linearly isomorphic to Therefore we regard Case(II)and Case(III)as the same class,denote the canonical domain If dim(iso(D))=4,given a linear isomorphism map σ :then aut(σ(D))has a group of bases Denote z=(u,v).In fact The one-parameter subgroup w(t)=is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values w(0)=z.We get the one-parameter analytic transformation:w(t)=zetK.Therefore Iso(σ(D))0is a real Lie group with dim(Iso(σ(D))0)=4: The one-parameter subgroup(u′(t),v′(t))=(t∈R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values(u′(0),v′(0))=(u,v),where 0 ≤ θ1<2π.Denote α1=eiθ1tght,t∈ R.The solution is where e1=(1,0),E11=diag{1,0}. The one-parameter subgroup(u′(t),v′(t))=exp(t(cosθ2+sinθ2))(t∈R)is a unique holomorphic solution of the complex ordinary differential equation systems with the initial values(u′(0),v′(0))=(u,v),where 0 ≤ θ2<2π.Denote α2=eiθ2tght,t∈ R.The solution is where e2=(0,1),E22=diag{0,1}. By Lemmas 2.5–2.6 and Theorem 3.2,we immediately get Theorem 2.2 again.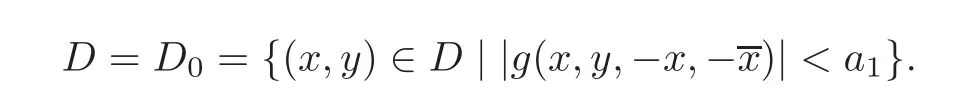
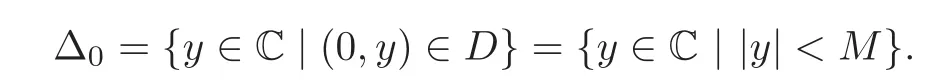
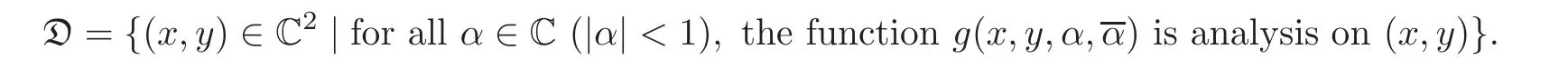
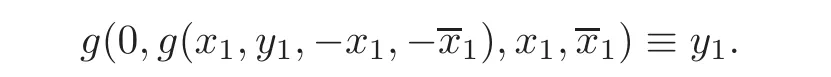
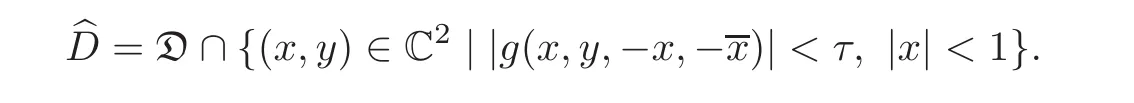
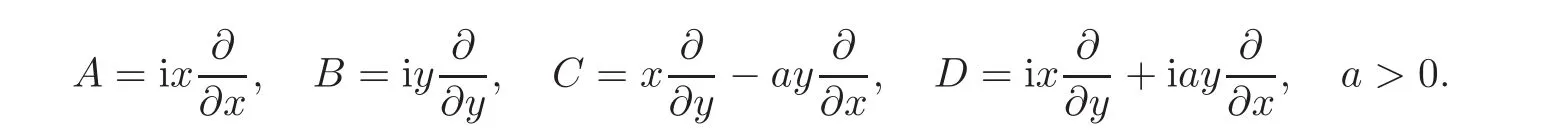

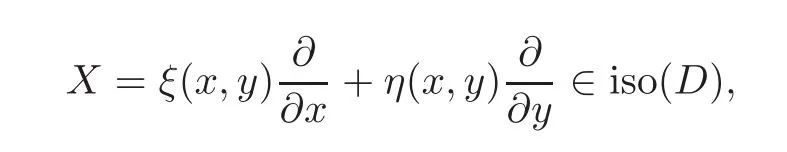
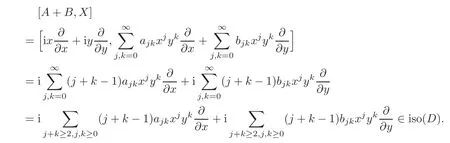

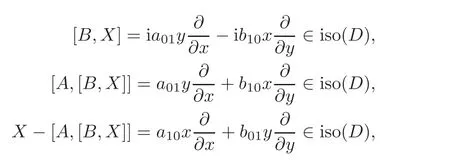
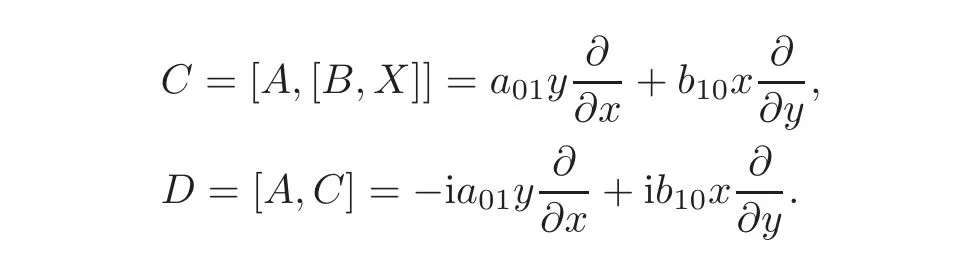
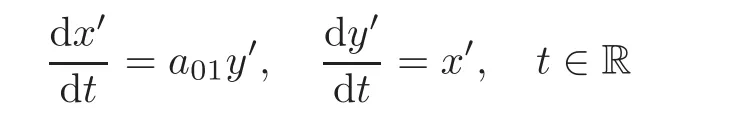
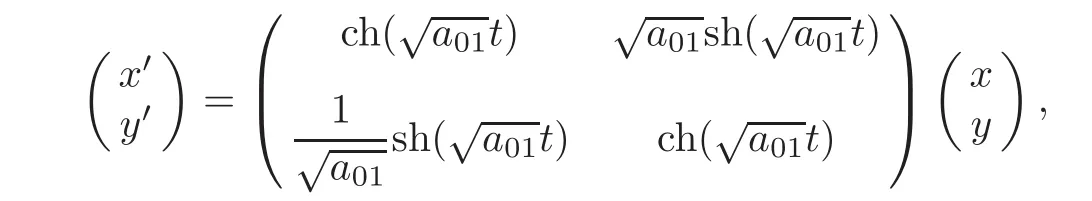
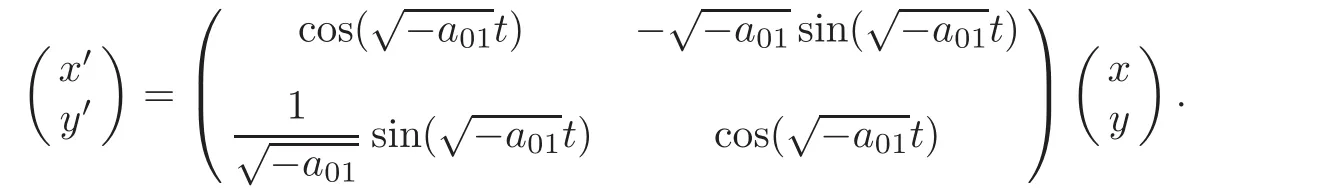
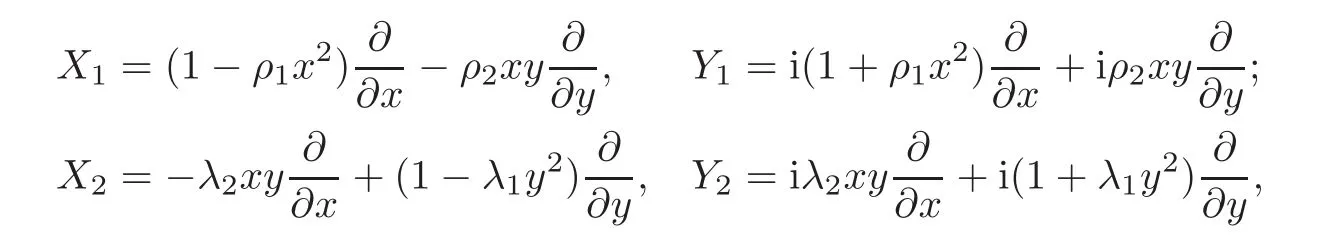
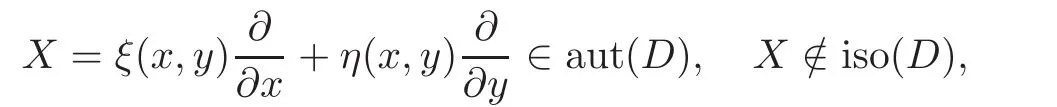
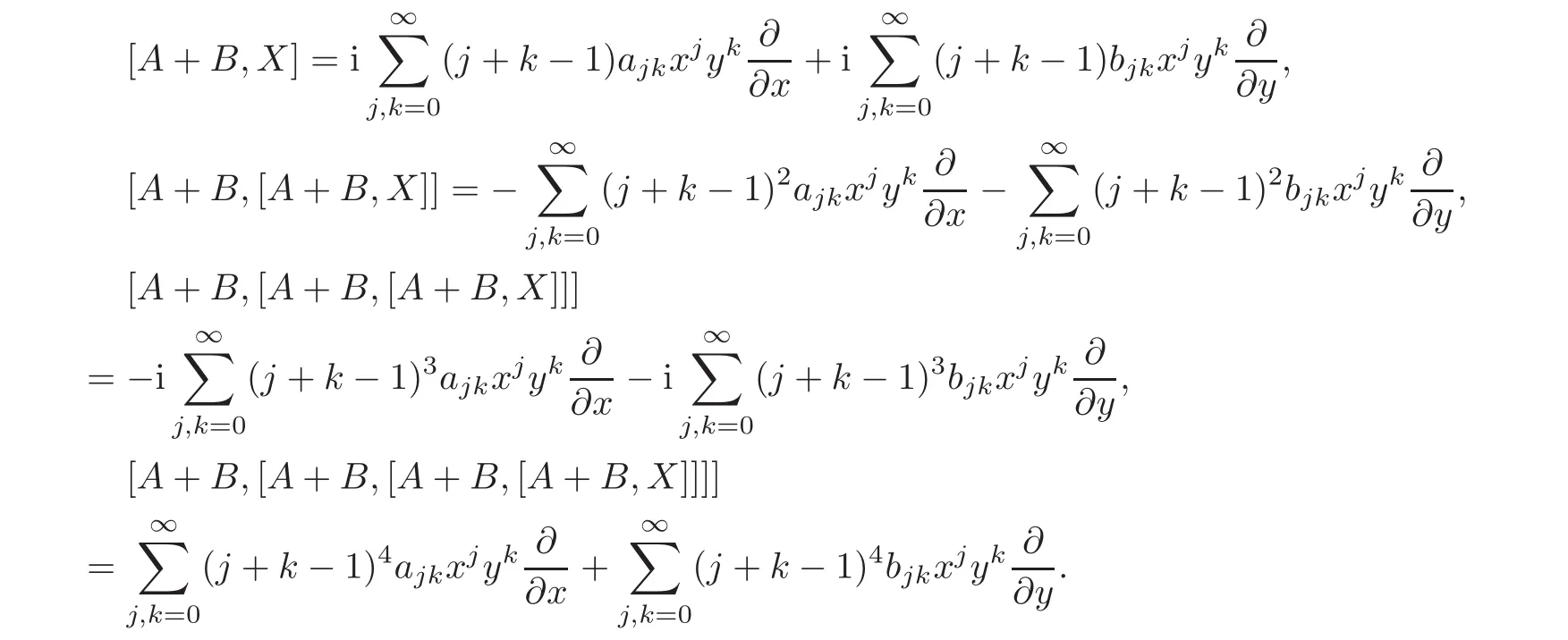
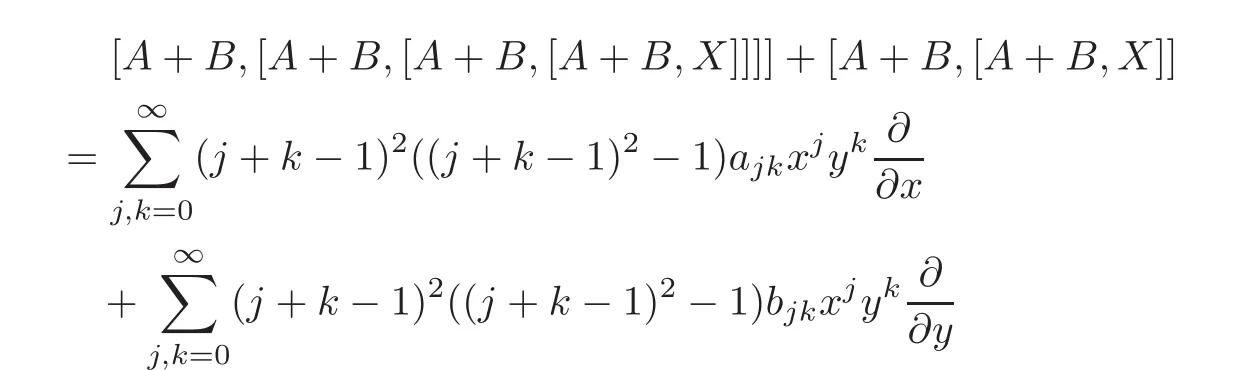

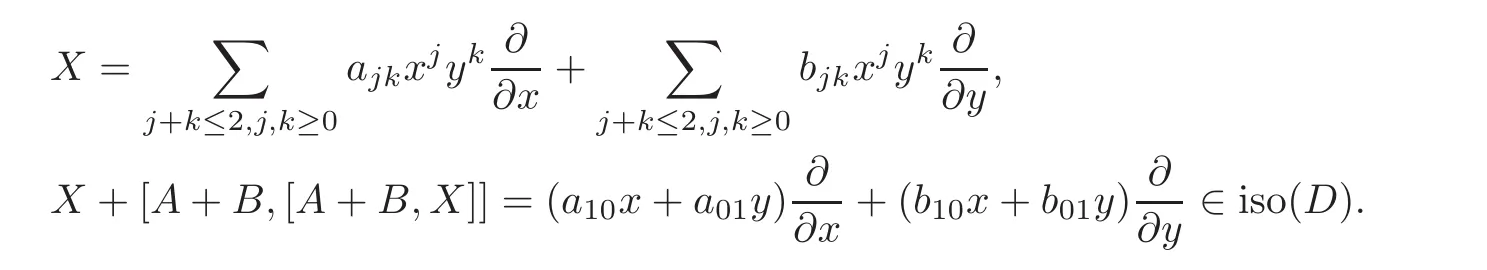
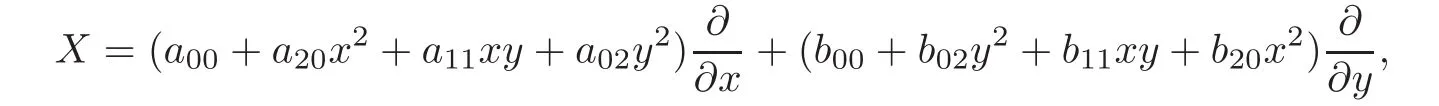
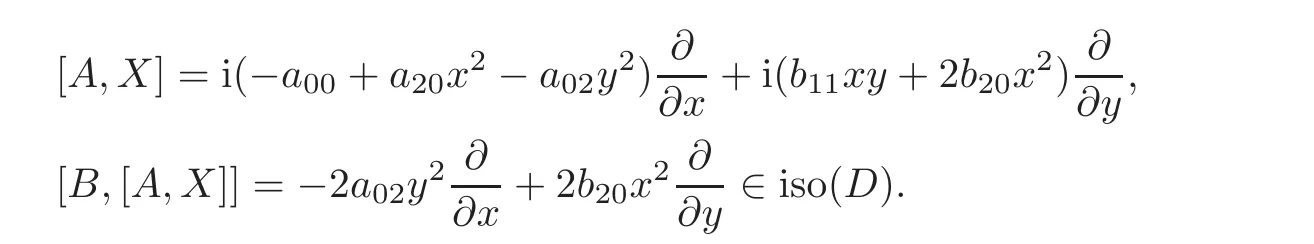
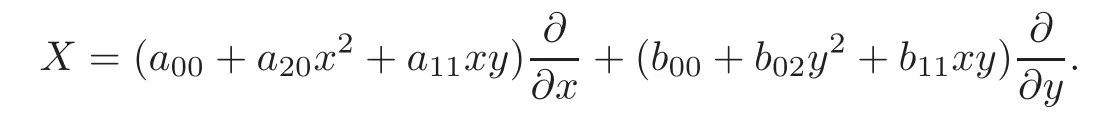

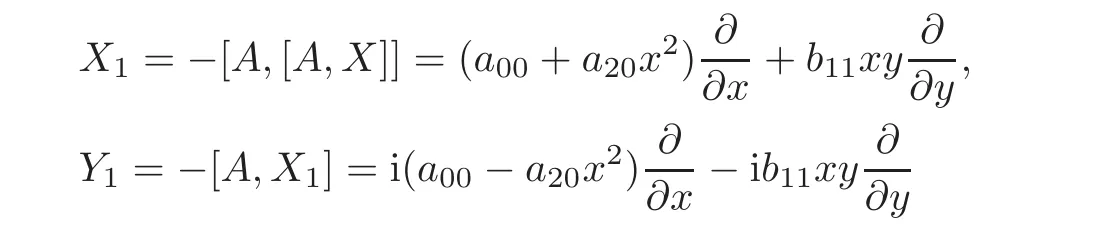
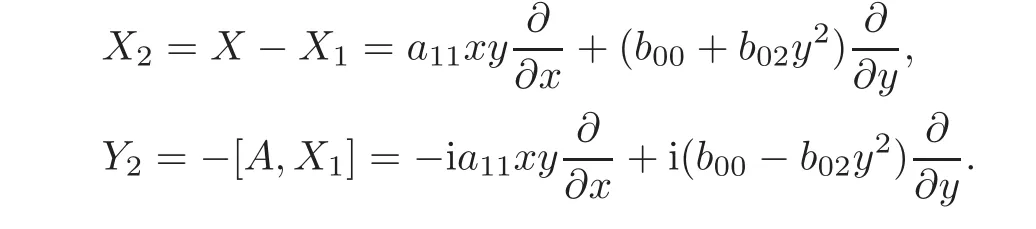
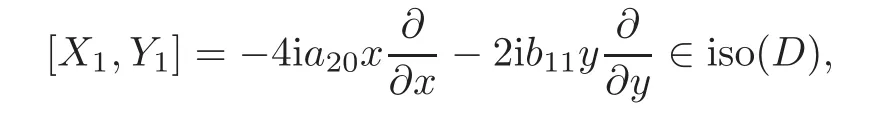
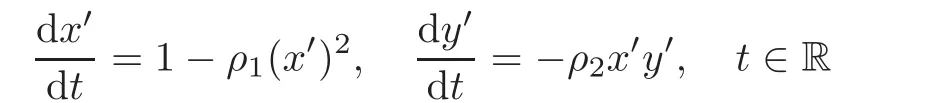
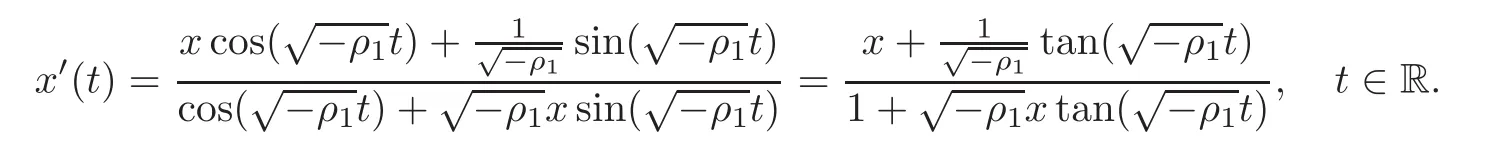
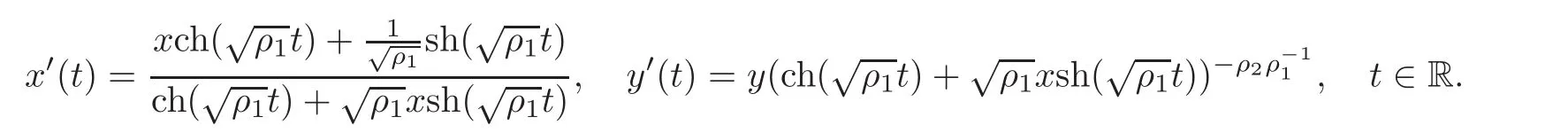
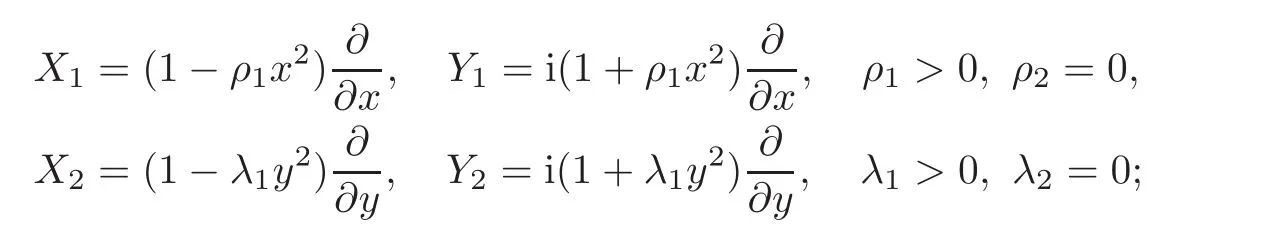

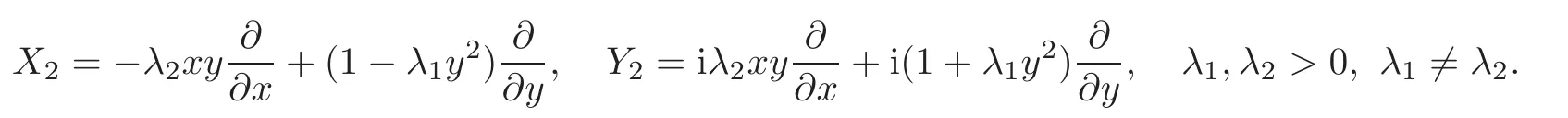
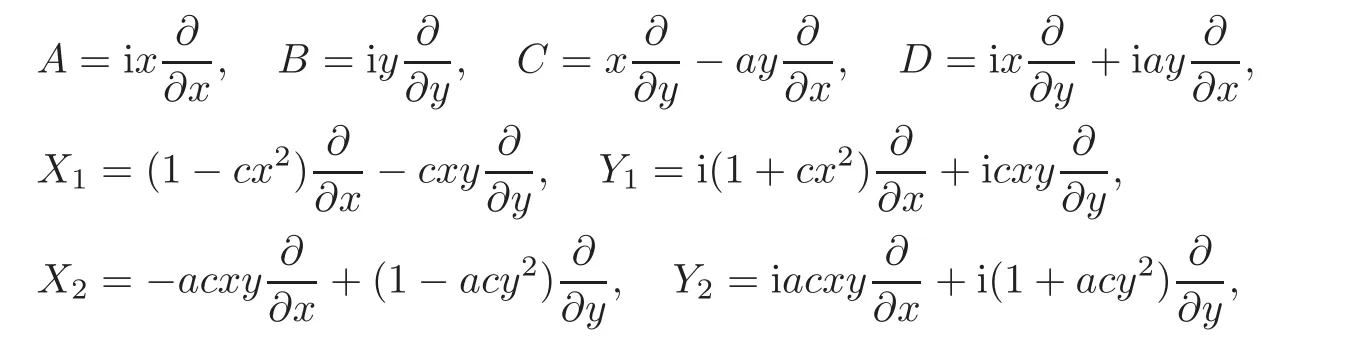
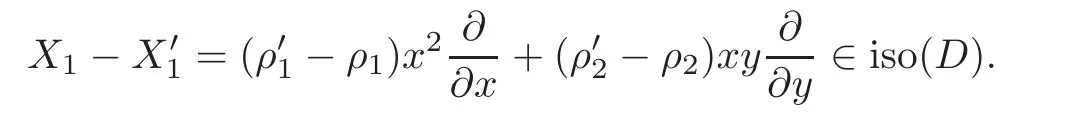
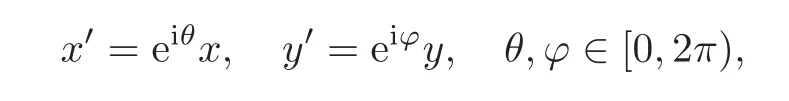
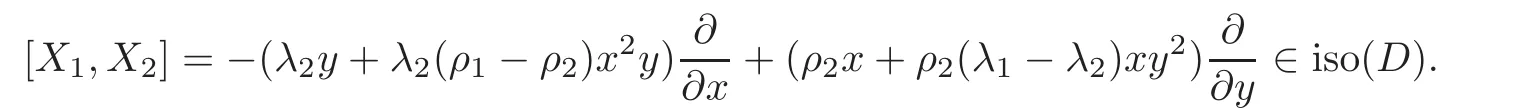
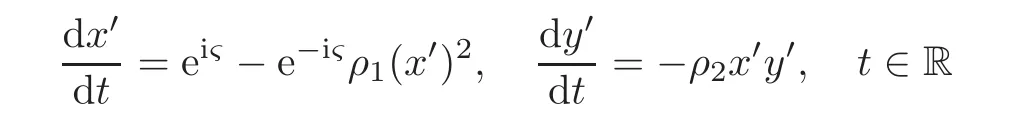
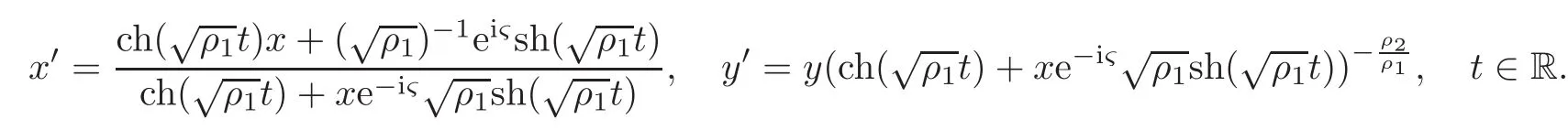


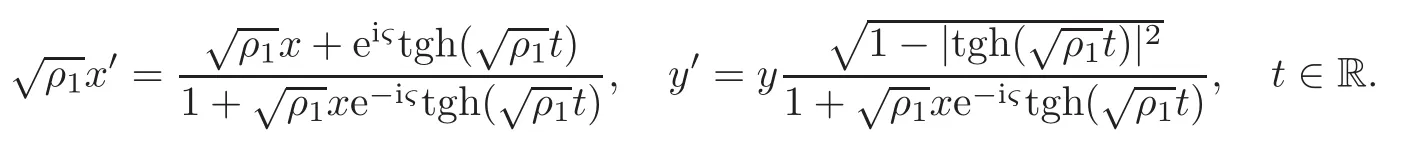
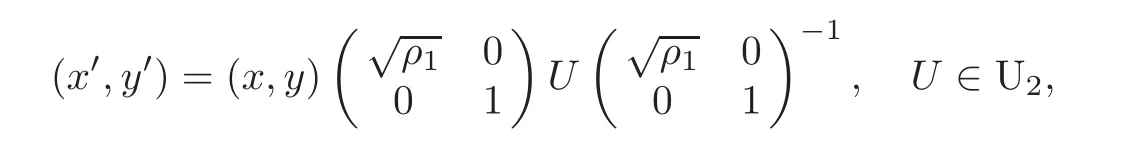
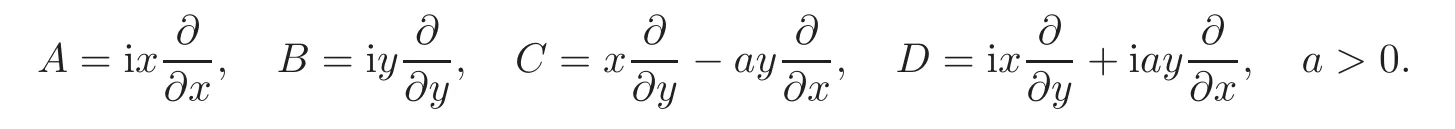
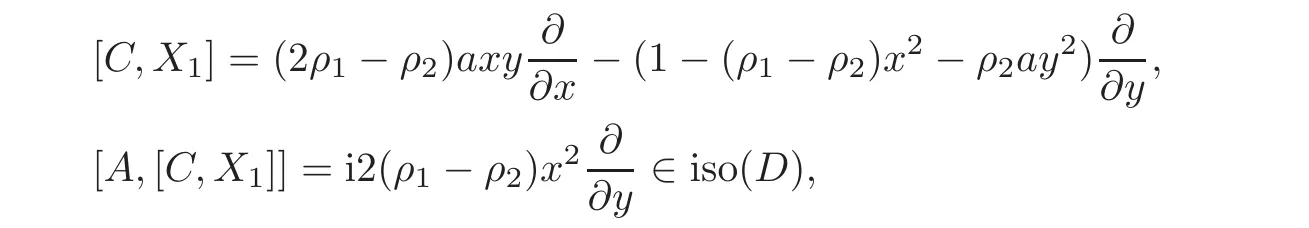

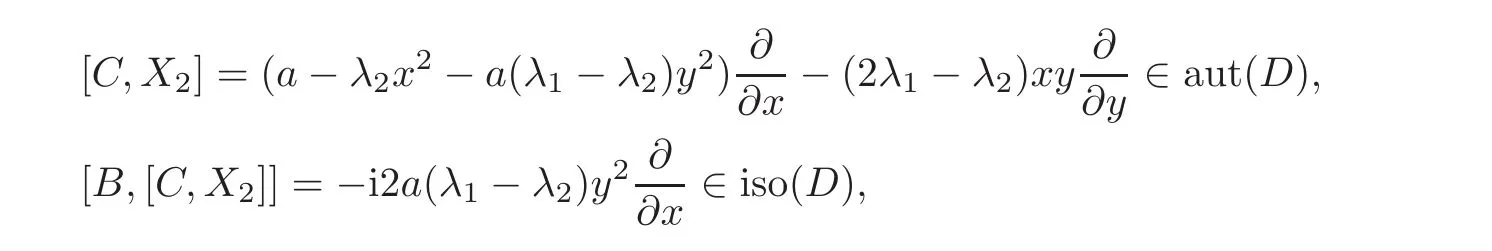
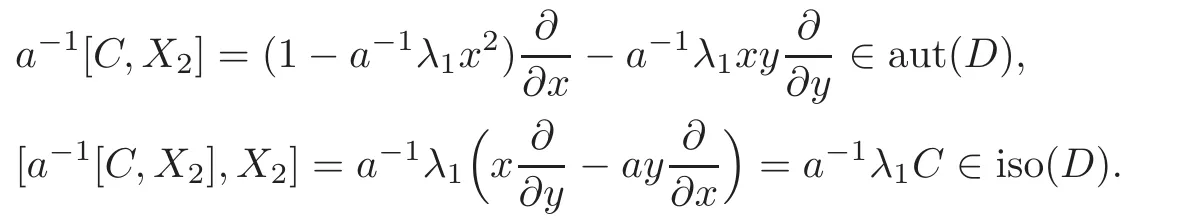
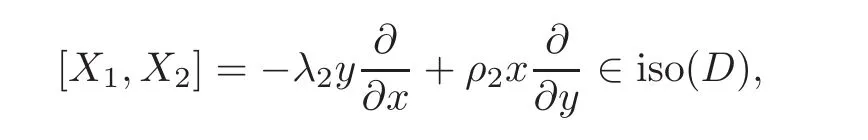
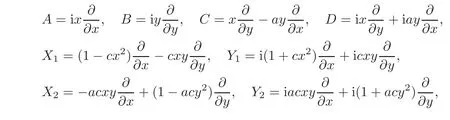
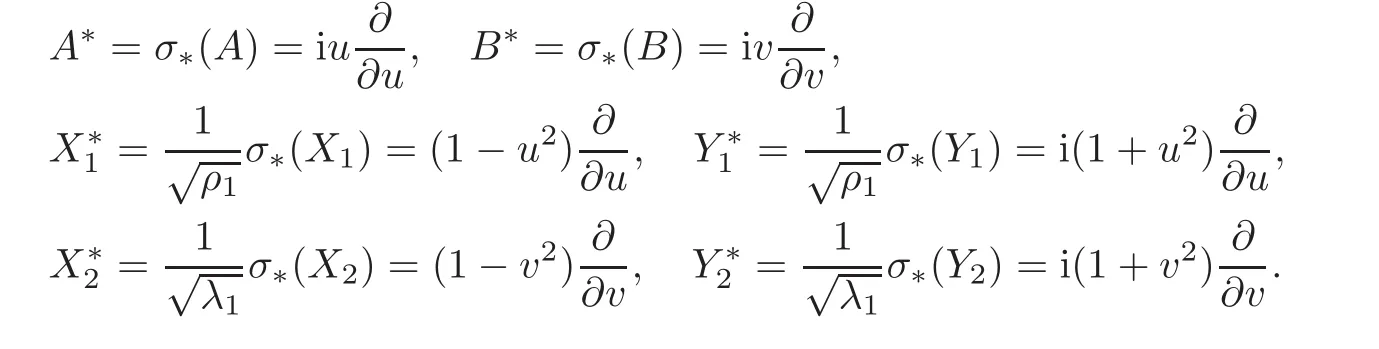
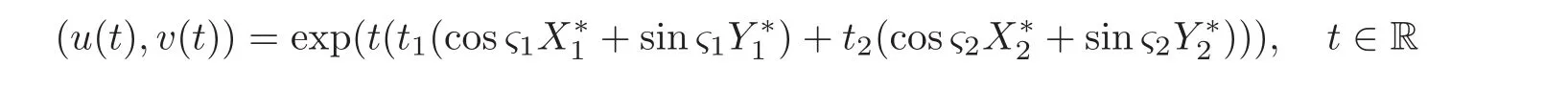
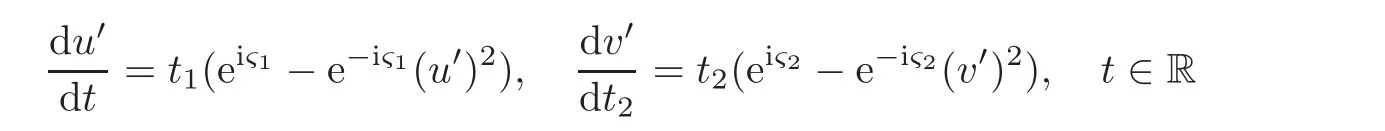
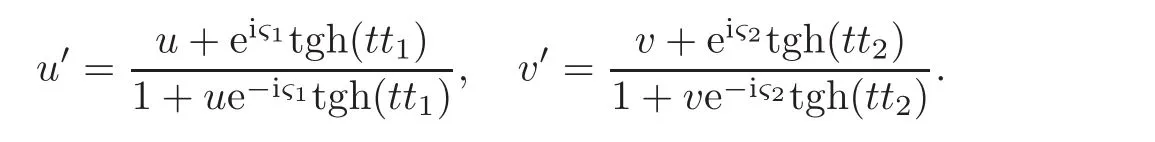
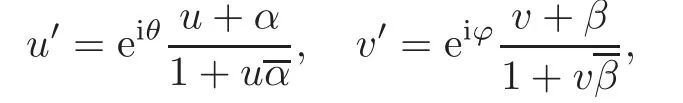
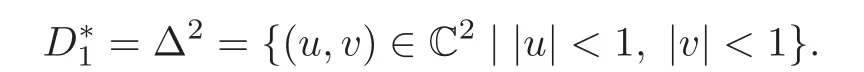
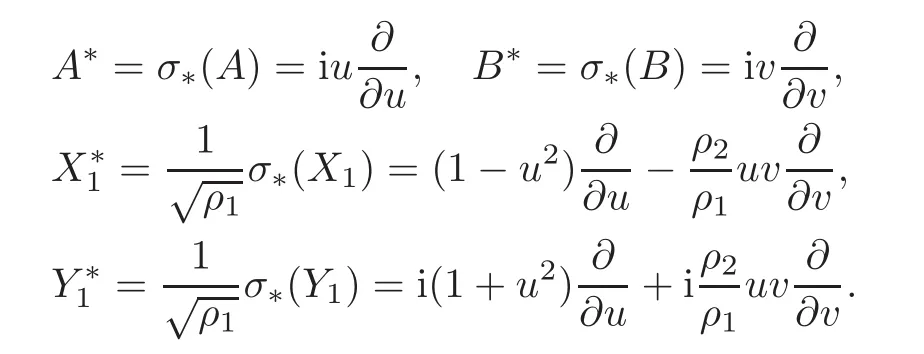

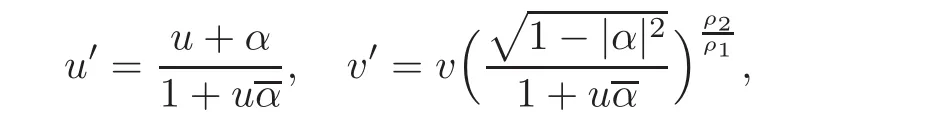
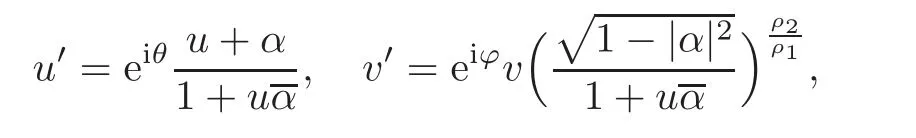
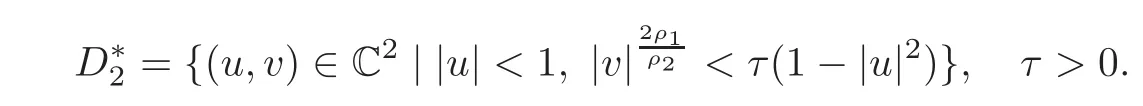

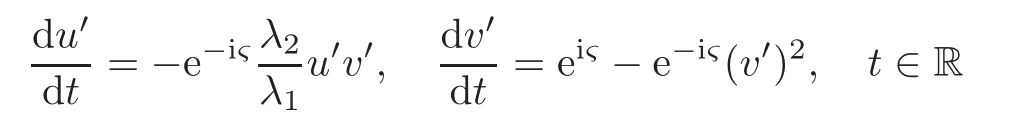
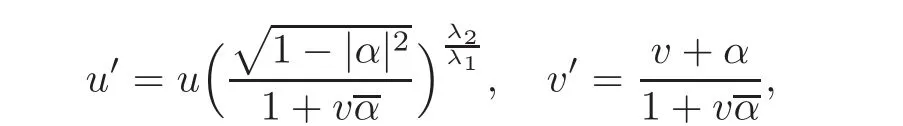

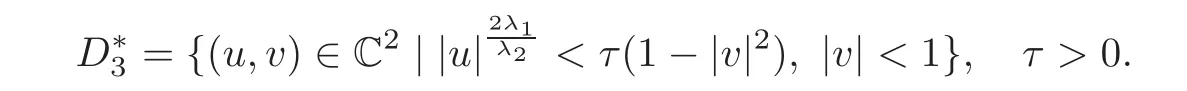
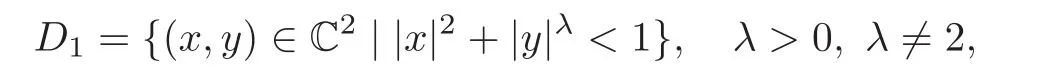
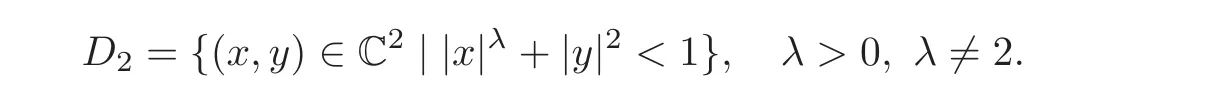
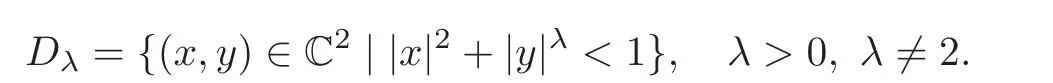
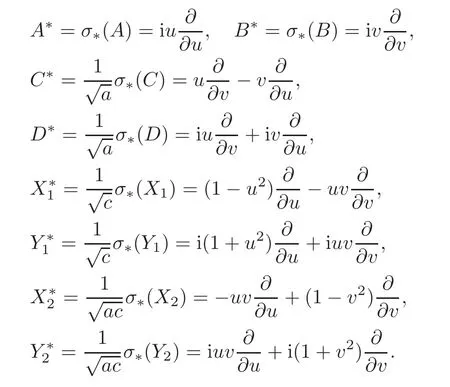
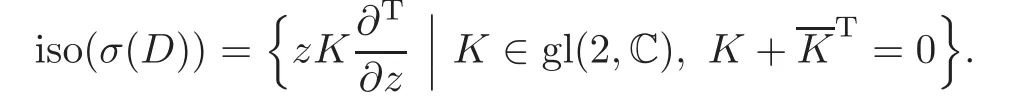
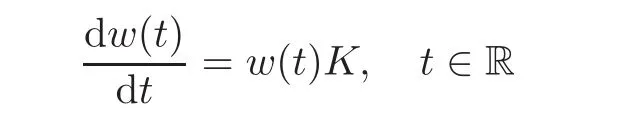

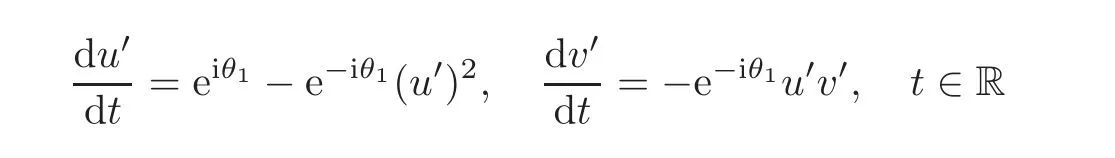
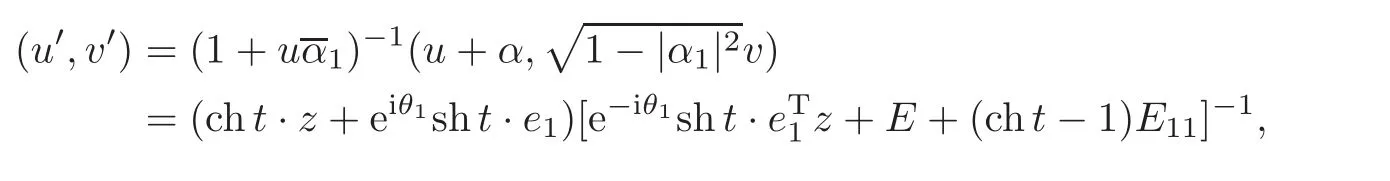
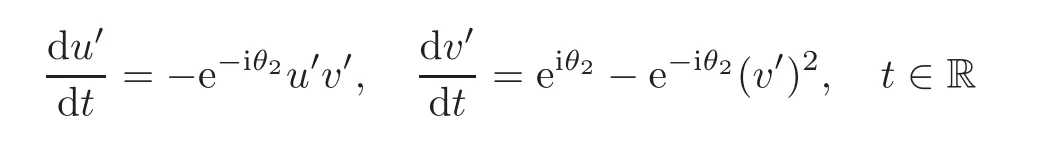
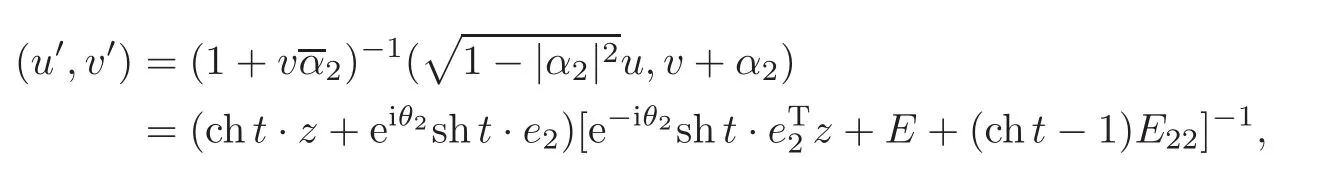
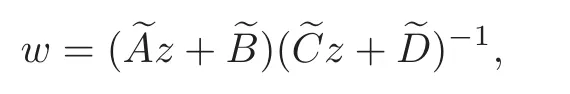
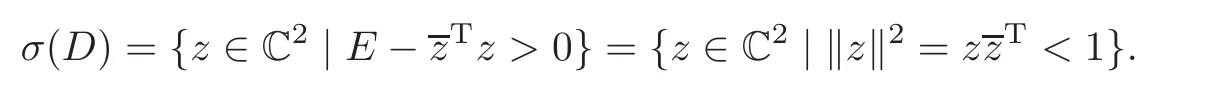
 Chinese Annals of Mathematics,Series B2018年4期
Chinese Annals of Mathematics,Series B2018年4期
