A Schwarz Lemma at the Boundary of Hilbert Balls∗
Zhihua CHEN Yang LIU Yifei PAN
Abstract In this paper,the authors prove a general Schwarz lemma at the boundary for the holomorphic mapping f between unit balls B and B′in separable complex Hilbert spaces H and H′,respectively.It is found that if the mapping f ∈ C1+α at z0 ∈ ∂B with f(z0)=w0 ∈ ∂B′,then the Fréchet derivative operator Df(z0)maps the tangent space Tz0(∂Bn)to Tw0(∂B′),the holomorphic tangent space T(1,0)z0 (∂Bn)to T(1,0)w0 (∂B′),respectively.
Keywords Boundary Schwarz lemma,Separable Hilbert space,Holomorphic mapping,Unit ball
1 Introduction
We begin with some notations.Let H be a separable complex Hilbert space.For any z,w∈H,the inner product and the corresponding norm are given by hz,wi,kzk=hz,zi12.Given c∈C,we have
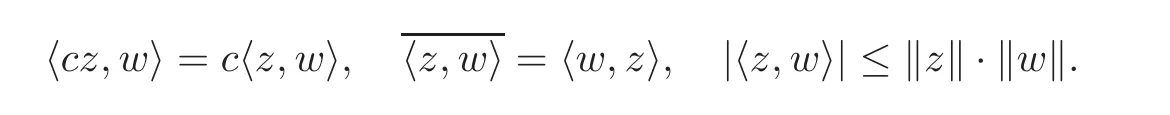
Two vectors a,b∈H are called orthogonal and we write a⊥b provided by ha,bi=0.For a subset E⊂H,the set E⊥is defined by
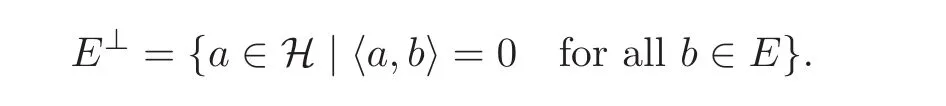
We choose a normal orthonormal basis e1,e2,···for H such that hei,eji= δijwhich equals 0 for i 6=j and equals 1 for i=j.Then for each z∈H,we write
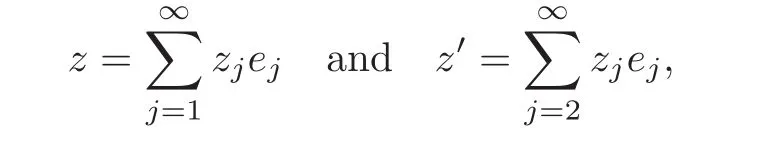
or denote z=(z1,z2,···)and z′=(z2,z3,···).For the other separable complex Hilbert space H′,its normal orthonormal basis is denoted by e′1,e′2,···.
Let V0be an open subset of H,and f be a continuous mapping of V0to H′.We say that f is a holomorphic mapping if for any z∈V0,there is a bounded linear operator Df(z)from H into H′such that
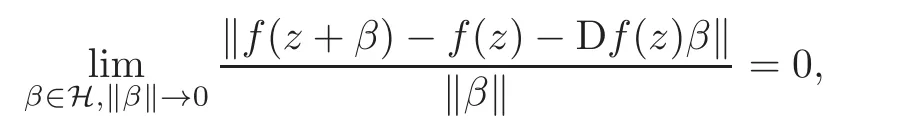
where k ·k is the norm of appropriate space.Df(z)denotes the Fréchet derivative of f at z,and Df(z)β is called the Fréchet derivative of f at z in the direction β.The chain rule of the Fréchet derivative is given as follows.
Lemma 1.1(see[1])Let H,H′,H′′be Hilbert spaces.Suppose f:V0⊂H→⊂H′andare differentiable maps.Then the composite g◦f is also differentiable and
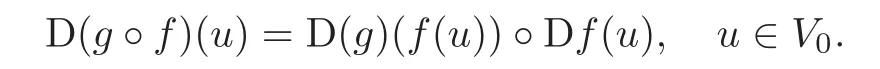
Denote by B(H,H′)the set of all bounded linear operators from H into H′.Then the adjoint of L∈B(H,H′)is the unique operator L∗:H′→H that satisfies
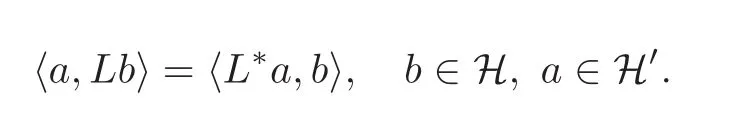
From the definition of Fréchet derivative,Df(z)is a bounded linear operator,and its adjoint is denoted by D∗f(z).
Let B={z∈ H|kzk<1}be the unit ball of H,∂B={z∈ H|kzk=1}be its boundary,and H(B,B′)be the set of all holomorphic mappings from B to B′.For an open subset V0⊂ H and 0<α<1,Cα(V0)is the set of all functions f on V0for which
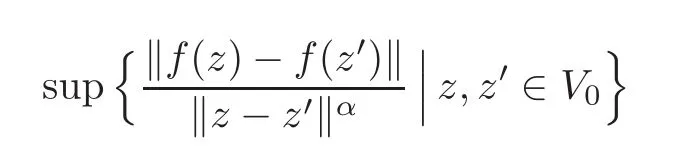
is finite.Ck+α(V0)is the set of all functions f on V0whose kth order partial derivatives exist and belong to Cα(V0)for an integer k≥0.
The Schwarz lemma is one of the most important results in complex analysis.A variant of the Schwarz lemma is known as the Schwarz-Pick lemma,which tells that a holomorphic selfmapping of the unit disk decreases the distance of points in the Poincaré metric.It has been generalized to the derivatives of arbitrary order in[2–3].When it comes to several complex variables,Rudin[4]gave a first derivative estimate for the bounded holomorphic functions on the polydisc,which is really a precursor to Schwarz-Pick lemma in high dimensions.On the other hand,the unit ball is a distinguished bounded domain,in which many interesting results are obtained(see[5]).For the Schwarz-Pick lemma of arbitrary order,[6–7]generalized Schwarz-Pick lemma to the holomorphic mappings on the unit ball in Cn.
On the other hand,the Schwarz lemma at the boundary is one of the popular topics in complex analysis(see[8]),which has been applied to geometric function theory of one complex variable and several complex variables(see[9]).The following result is the classical boundary version of the Schwarz lemma in one complex variable.
Theorem 1.1(see[8])Let D be the unit disk in C,and f be the self-holomorphic mapping of D.If f is holomorphic at z=1 with f(0)=0 and f(1)=1,then f′(1)≥ 1.
Some multidimensional generalizations of the Schwarz lemma at the boundary in several complex variables were given by[9–12]recently.In[13],the high order Schwarz-Pick lemma for holomorphic mappings between Hilbert balls was studied.However,the boundary Schwarz lemma for in finite dimensions Hilbert spaces is open and challenging,and in this paper,we study it for separable complex Hilbert spaces.
For z0∈ ∂B,the tangent space Tz0(∂B)and holomorphic tangent space(∂B)at z0are defined by
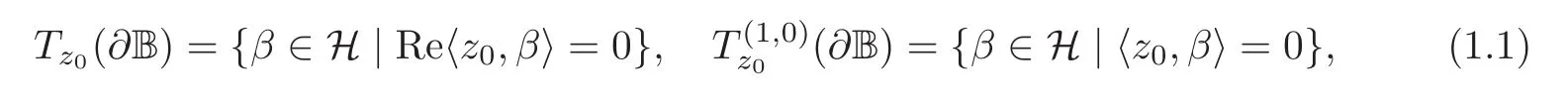
respectively.In this paper,we study the mapping f ∈ H(B,B′).Our main results are listed as follows.
Theorem 1.2 Let f ∈ H(B,B′).If f is C1+αat z0∈ ∂B and f(z0)=w0∈ ∂B′,then it shows
(I)Df(z0)β ∈ Tw0(∂B′)for any β ∈ Tz0(∂B),and Df(z0)β ∈(∂B′)for any β ∈(∂B).
(II)There exists λ ∈ R such that D∗f(z0)w0= λz0with λ ≥>0 where a=f(0)and D∗f(z0)is the adjoint operator of Df(z0).
We notice that for H=H′=C,the theorem tells f′(z0)>0,so the image f(∂B)at w0is always smooth.However,it is not necessarily true for Cnwith n≥2.This theorem can be regarded as a general Schwarz lemma at the boundary for holomorphic mappings between unit balls in separable complex Hilbert spaces.It shows that the Fréchet derivative operator preserves tangent space and holomorphic tangent space at the boundary of the unit balls.When H=H′=Cn,as a special case considered in this paper,Theorem 1.2 reduces(1)and(2)in[9,Theorem 3.1].For H=H′=C,part(II)of the theorem gives Theorem 1.1 from[8].
2 Preliminaries
Before proving the main results,we give some preparation.Lemma 2.1 was given in[13]for p∈B.
Lemma 2.1 For given p ∈ B∪∂B and q∈ H with q 6=0,let L(ξ)=p+ξq for ξ∈ C.Then
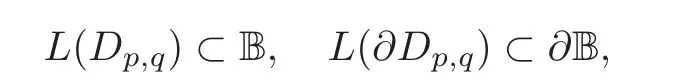
Proof Assume kL(Dp,q)k2<1,which means
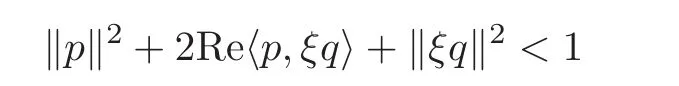
and

i.e.,
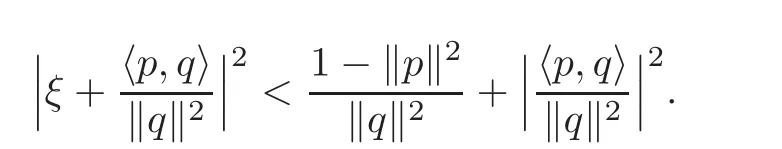
The proof is finished.
Let φz(w)be the automorphism of B,and
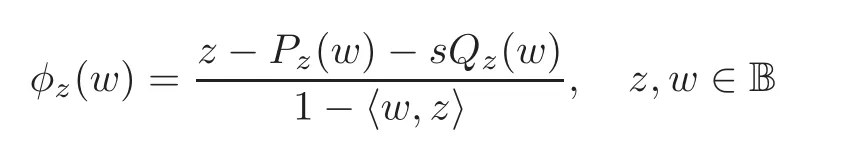
with Pzbeing the orthogonal projection of H by
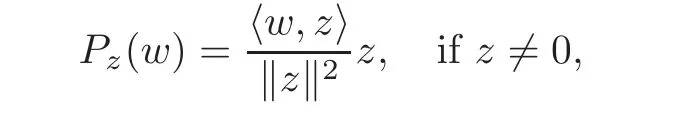
Qz=I−Pzwith I being the identity mapping,and(see[5]).It is found that φz(0)=z, φz(z)=0 and φz=.For simplicity,motivated by[14],we can rewrite φz(w)by

where Γ ∈ B(H,H)is expressed byThen it is easy to obtained that

From(2.1),for a fixed z∈B and any w∈B,
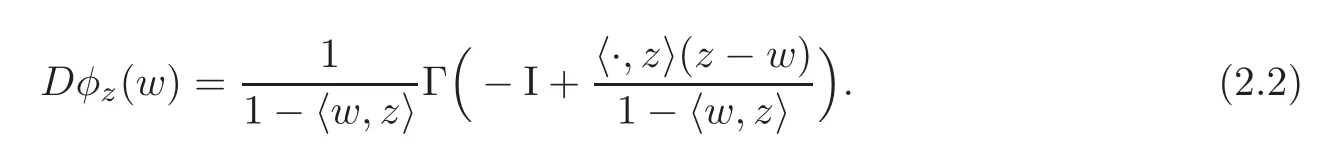
Lemma 2.2 If f∈H(B,B′)and f(0)=0,then kf(w)k≤kwk,w ∈B.
It is a well-known Schwarz type result(see[5]),and we give a simple proof here.
Proof The Kobayashi distances for the unit ball in H could be expressed by
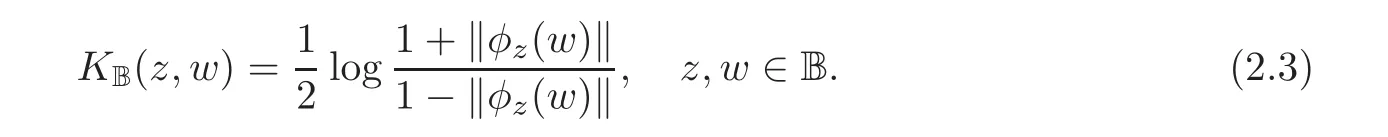
It is the fact that the Kobayashi distance decreases under holomorphic mappings(see[15]).By(2.3),we have KB′(0,f(w)) ≤ KB(0,w),i.e.,
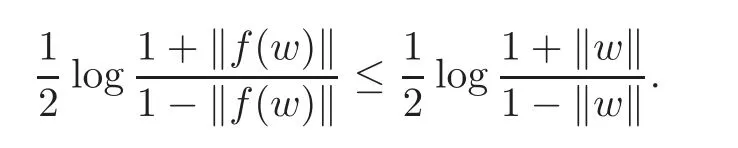
Lemma 2.3 Given any b ∈ H and a ∈ H′,we have the operator A=h·,bia ∈ B(H,H′)and
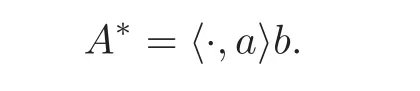
Proof From the definition of the inner product,it is easy to see A ∈ B(H,H′).For any y∈ H and x∈ H′,
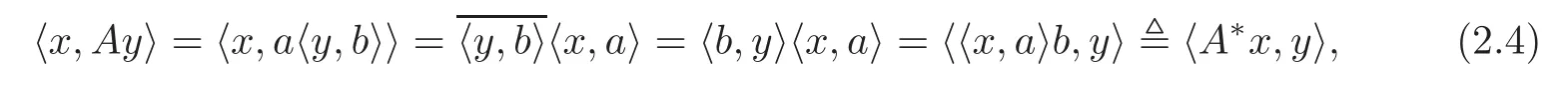
which gives A∗=b from the uniqueness of A∗.
If A=h·,biac with c ∈ C,Lemma 2.3 also gives A∗=h·,aibc.
3 Proof of Theorem 1.2
In the following,we will prove Theorem 1.2 in five steps.
Step 1 Assume z0=e1∈ ∂B,and f is C1+αin a neighborhood V of z0.Moreover,we assume f(0)=0 and f(z0)=w0=
Let p=z0,q=(−1+ik)z0for any given k∈ R.Then p+tq=(1−t+ikt)z0for t∈ R.From Lemma 2.1,kp+tqk<1⇔|1−t+ikt|<1⇔0 By Lemma 2.2, i.e., Substituting w0=z0=e1and letting t→ 0+,we have i.e., which gives Since(3.1)is valid for any k∈R,we have which implies and Step 2 Let p=z0,q=−z0+ikejfor j≥2 and k∈R.Then p+tq=(1−t)z0+iktejfor t∈R.By Lemma 2.1,kp+tqk<1⇔|1−t|2+|ikt|2<1⇔0 By Lemma 2.2, i.e., Using w0=z0=e1and letting t→ 0+,it follows that i.e., With a similar argument to Step 1,we have Meanwhile,if we assume p=z0,q=−z0+kejfor j≥2 and any k∈R.It is easy to find Therefore Combining(3.2)and(3.3),and using the adjoint operator D∗f(z0)of Df(z0),one gets Therefore Step 3 Now let z0be any given point at∂B which is not necessary e1.Then there exists a unitary matrix Uz0such that Uz0(z0)=e1.Assume f(0)=0,f(z0)=w0∈ ∂B′,which is not necessary.Similarly,there is a Uw0such that Uw0(w0)=Denote Then g(0)=0,g(e1)=.Moreover From Steps 1 and 2,we have i.e., Step 4 Let f(z0)=w0with z0∈ ∂B,w0∈ ∂B′.If f(0)=a 6=0,then we use the automorphism of B′to get the result.Assume that φa(w)is an automorphism of B′such that φa(a)=0.Then φa(w0)∈ ∂B′and there exists a Uφasuch that Uφa(φa(w0))=w0.Let then h(0)=0,h(z0)=w0.As a result of Step 3,there is a real number γ ≥ 1 such that According to the expression of h,it is obtained that Since Uφa(φa(w0))=w0,we haveTherefore, From(2.2)and Lemma 2.3, It comes from(2.1)that Combining with(3.5)we get for some γ≥1.As a result, Step 5 For any β ∈ Tz0(∂B),from the definition of tangent space given by(1.1),we have To prove Df(z0)β ∈ Tw0(∂B′),it is sufficient to verify From(3.6),D∗f(z0)w0= λz0with λ >0,which gives It comes from the above equation that We decompose H=e1C ⊕ F,where F=In this decomposition,z=(z1,z′) ∈ H with z1∈ C and z′∈ F.Then the upper half-plane H of H could be described by{z∈ H|Imz1>Similar notations are given for H′. The tangent space T0(∂H)and holomorphic tangent space(∂H)at 0 are defined by respectively.The boundary version of Schwarz lemma on the upper half-plane is given as follows. Theorem 4.1 Let g∈ H(H,H′)for H ∈ H and H′∈ H′respectively.If g is C1+αat 0∈ ∂H and g(0)=0∈ ∂H′,then it holds that (I)Dg(0)β ∈ T0(∂H′)for any β ∈ T0(∂H),and Dg(0)β ∈for any β ∈ (II)There exists λ ∈ R such that D∗g(0)()= λ(−ie1)with,where Proof First,there exists a biholomorphic mapping(Cayley transform)Φ:B→H given by and Φ−1(0)=e1. Step 1 Let g(w) ∈ H(H,H′)which is also C1+αat 0.We assume g(0)=0 and g(ie1)=Construct a mapping then f ∈ H(B,B′)and f(0)=0,f(e1)=.From(3.4)we have Substituting(4.3)into(4.2)gives i.e., where λf≥ 1 and −ie1denotes the normal vector of H at 0. Step 2 If g(0)=0 and g(ie1)we assume g(ie1)=b.Consider the mapping given by(4.1),thenFrom(3.6)we have In addition,from(4.3),one gets i.e., The proof of part(I)is the same as that of Theorem 1.2,and it is omitted here. Acknowledgements The work was finished while the second author visited the third author at the department of mathematical sciences,Indiana University–Purdue University Fort Wayne.The first author appreciates the comfortable research environment and all support provided by the institution in the 2014 academic year.
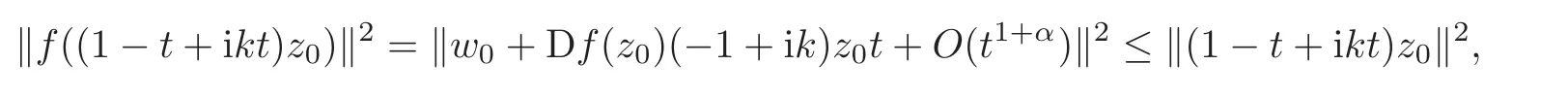
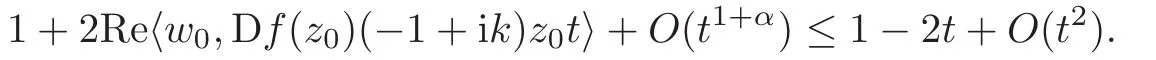
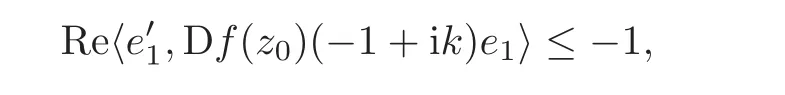
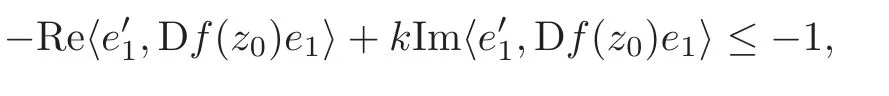
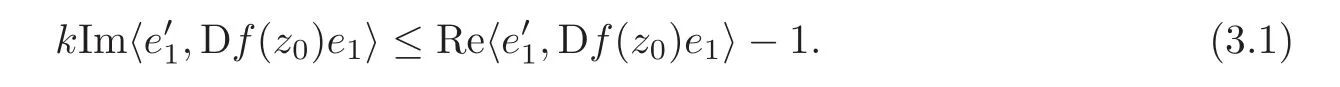
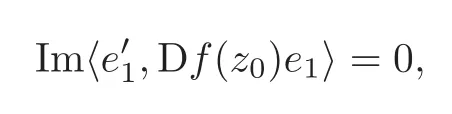
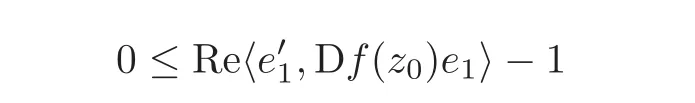

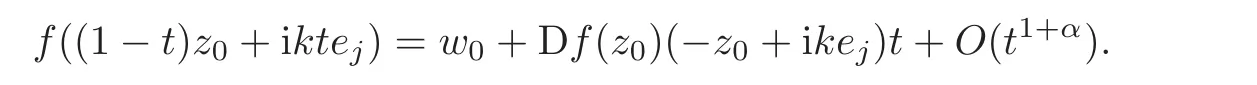
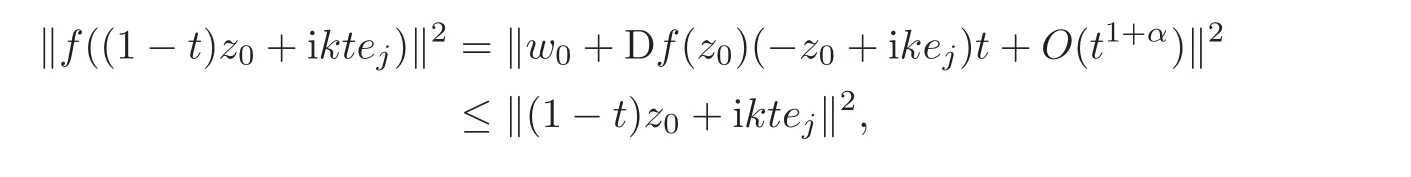
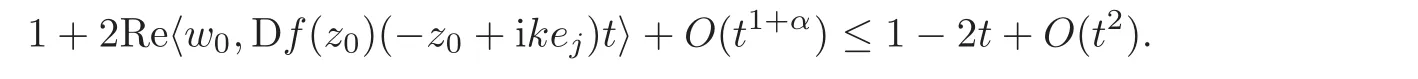
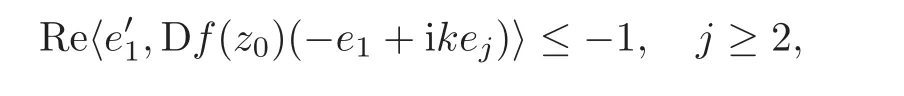
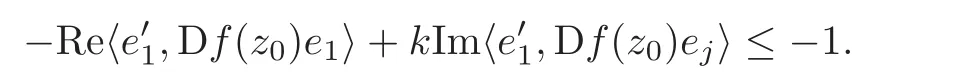
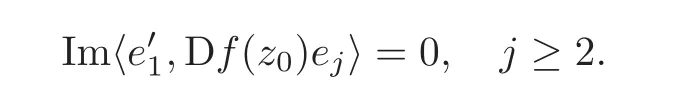


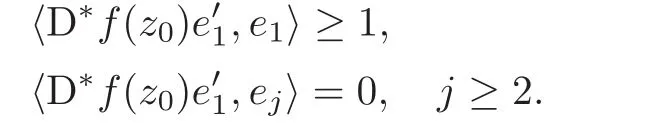
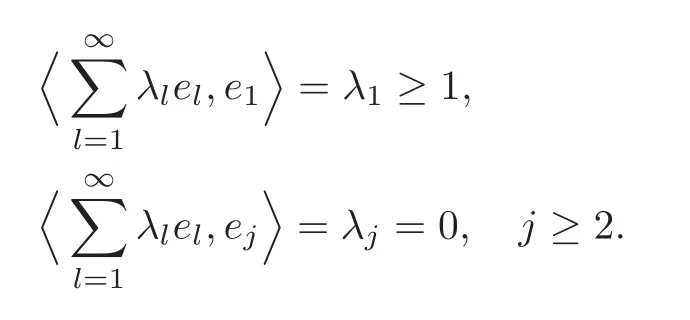

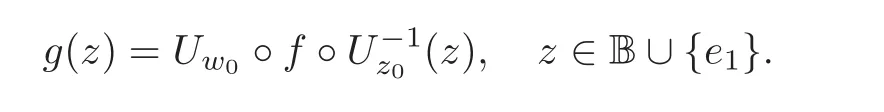
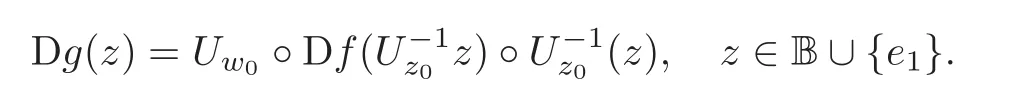

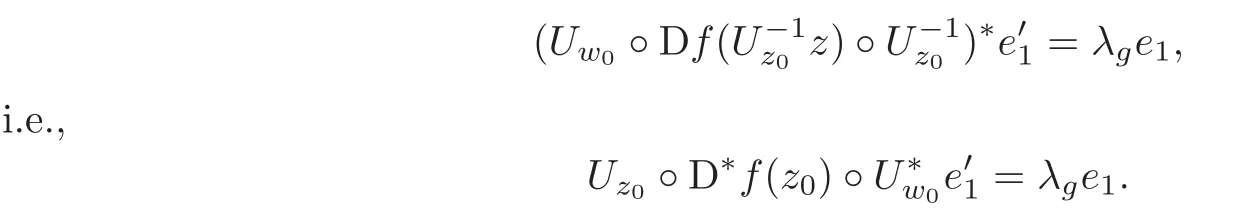
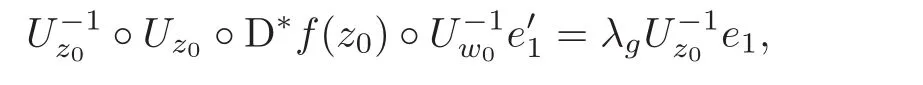


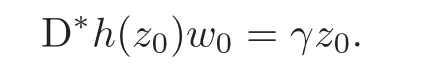
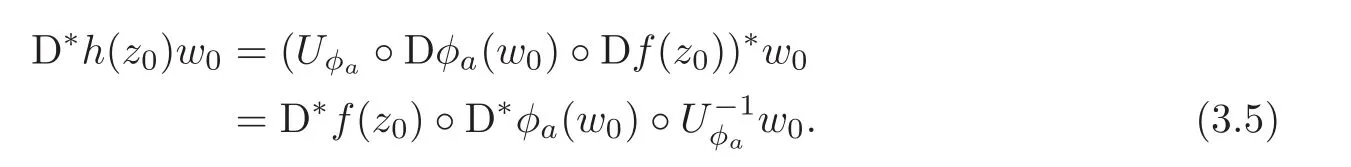
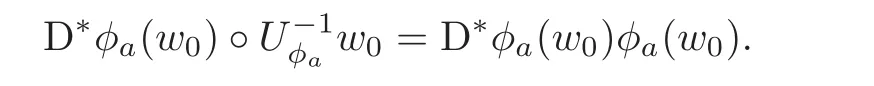
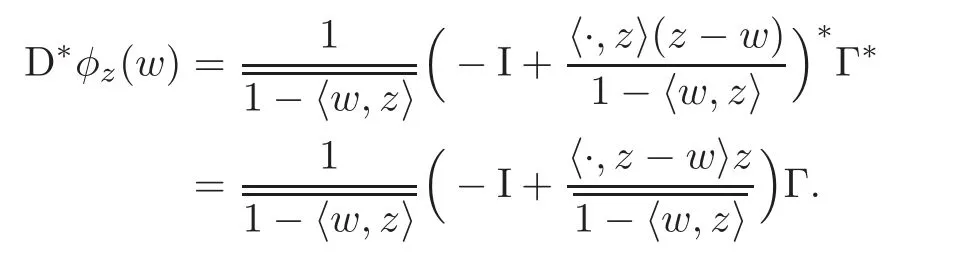
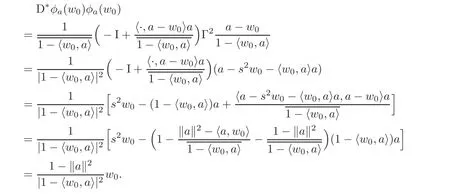


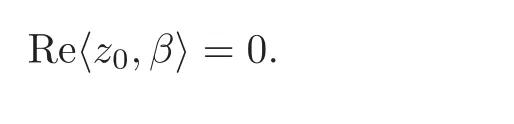

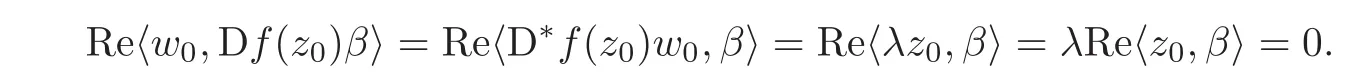
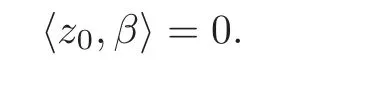
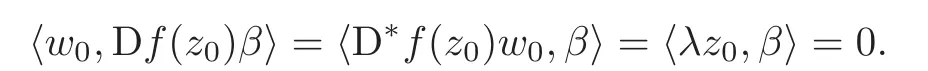
4 The Boundary Version of Schwarz Lemma on the Upper Half-Plane
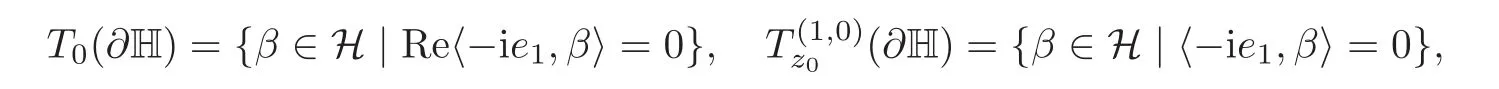

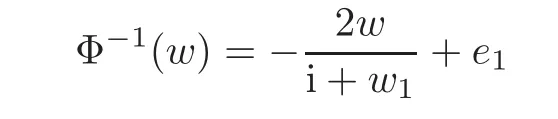


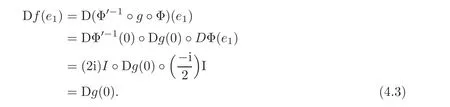
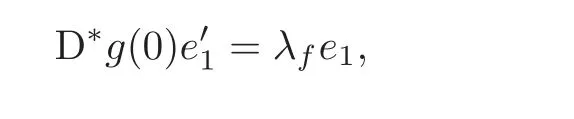
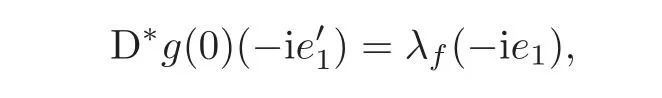
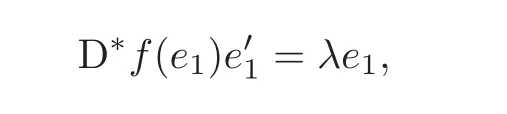
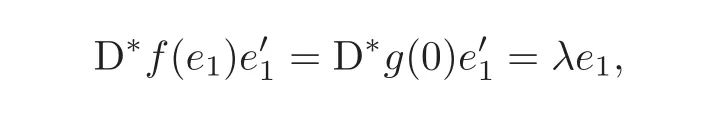
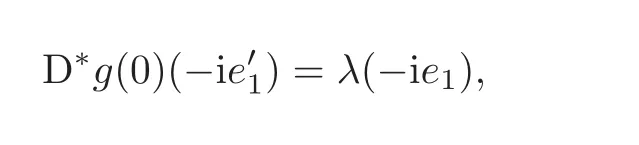
 Chinese Annals of Mathematics,Series B2018年4期
Chinese Annals of Mathematics,Series B2018年4期
