Nonlinear Maps Preserving the Jordan Triple∗-Product on Factor von Neumann Algebras∗

Changjing LI Quanyuan CHEN Ting WANG

Abstract Let A and B be two factor von Neumann algebras.For A,B∈A,define by[A,B]∗=AB −BA∗the skew Lie product of A and B.In this article,it is proved that a bijective map Φ :A → B satisfies Φ([[A,B]∗,C]∗)=[[Φ(A),Φ(B)]∗,Φ(C)]∗ for all A,B,C ∈ A if and only if Φ is a linear ∗-isomorphism,or a conjugate linear ∗-isomorphism,or the negative of a linear∗-isomorphism,or the negative of a conjugate linear∗-isomorphism.

Keywords Jordan triple∗-product,Isomorphism,von Neumann algebras

1 Introduction

Let A be a ∗-algebra and η be a non-zero scalar.For A,B ∈ A,define the Jordan η-∗-product of A and B by A♦ηB=AB+ ηBA∗.The Jordan(−1)-∗-product,which is customarily called the skew Lie product,was extensively studied because it naturally arises in the problem of representing quadratic functionals with sesquilinear functionals(see[9–11])and in the problem of characterizing ideals(see[2,8]).We often write the Jordan(−1)-∗-product by[A,B]∗,that is[A,B]∗=AB −BA∗.A not necessarily linear map Φ between ∗-algebras A and B is said to preserve the Jordan η-∗-product if Φ(A♦ηB)= Φ(A)♦ηΦ(B)for all A,B ∈ A.Recently,many authors have started to pay more attention to the maps preserving the Jordan η-∗-product between ∗-algebras(see[1,3,6–7]).In[3],Dai and Lu proved that if Φ is a bijective map preserving the Jordan η-∗-product between two von Neumann algebras,one of which has no central abelian projections,then Φ is a linear ∗-isomorphism if η is not real and Φ is a sum of a linear ∗-isomorphism and a conjugate linear ∗-isomorphism if η is real.

Recently,Huo et al.[5]studied a more general problem.They considered the Jordan triple η-∗-product of three elements A,B and C in a ∗-algebra A defined by A♦ηB♦ηC=(A♦ηB)♦ηC(we should be aware that♦ηis not necessarily associative).A map Φ between ∗-algebras A and B is said to preserve the Jordan triple η-∗-product if Φ(A♦ηB♦ηC)= Φ(A)♦ηΦ(B)♦ηΦ(C)for all A,B,C ∈ A.Clearly a map between ∗-algebras preserving the Jordan η-∗-product also preserves the Jordan triple η-∗-product.However,the map Φ :C → C,Φ(α+βi)= −4(α3+β3i)is a bijection which preserves the Jordan triple(−1)-∗-product and Jordan triple 1-∗-product,but it does not preserve the Jordan(−1)-∗-product or Jordan 1-∗-product.So,the class of those maps preserving the Jordan triple η-∗-product is,in principle wider than the class of maps preserving the Jordan η-∗-product.

In[5],let η 6= −1 be a non-zero complex number,and let Φ be a bijection between two von Neumann algebras,one of which has no central abelian projections,satisfying Φ(I)=I and preserving the Jordan triple η-∗-product.Huo et al.showed that Φ is a linear ∗-isomorphism if η is not real and Φ is the sum of a linear ∗-isomorphism and a conjugate linear ∗-isomorphism if η is real.On the one hand,Huo et al.did not consider the case η = −1.However,the Jordan(triple)(−1)-∗-product is the most meaningful and important in Jordan(triple) η-∗-products.On the other hand,it is easy to see that a map Φ preserving the Jordan triple η-∗-product does not need to satisfy Φ(I)=I.Indeed,let Φ(A)= −A for all A ∈ A.Then Φ preserves the Jordan triple η-∗-product but Φ(I)= −I.Because of the above two reasons,in this paper,we will discuss maps preserving the Jordan triple(−1)-∗-product without the assumption Φ(I)=I.We mainly prove that a bijective map Φ between two factor von Neumann algebras preserves the Jordan triple(−1)-∗-product if and only if Φ is a linear ∗-isomorphism,or a conjugate linear∗-isomorphism,or the negative of a linear ∗-isomorphism,or the negative of a conjugate linear∗-isomorphism.

As usual,R and C denote respectively the real field and complex field.Throughout,algebras and spaces are over C.A von Neumann algebra A is a weakly closed,self-adjoint algebra of operators on a Hilbert space H containing the identity operator I.A is a factor von Neumann algebra means that its center contains only the scalar operators.It is clear that if A is a factor von Neumann algebra,then A is prime,that is,for A,B∈A if AAB={0},then A=0 or B=0.

2 The Main Result and Its Proof

To complete the proof of main theorem,we need two lemmas.

Lemma 2.1 Let A be an arbitrary factor von Neumann algebra with the identity operator I and A∈A.If AB=BA∗for all B∈A,then A∈RI.

Proof In fact,take B=I,then A=A∗.So AB=BA for all B ∈ A,which implies A belongs to the center of A.Note that A is a factor,it follows that A∈RI.

Lemma 2.2(see[4,Problem 230]) Let A be a Banach algebra with the identity I.If A,B ∈ A and λ ∈ C are such that[A,B]= λI,where[A,B]=AB −BA,then λ =0.

The main result in this paper is as follows.

Theorem 2.1 Let A and B be two factor von Neumann algebras.Then a bijective map Φ :A → B satisfies Φ([[A,B]∗,C]∗)=[[Φ(A),Φ(B)]∗,Φ(C)]∗for all A,B,C ∈ A if and only if Φ is a linear∗-isomorphism,or a conjugate linear∗-isomorphism,or the negative of a linear∗-isomorphism,or the negative of a conjugate linear ∗-isomorphism.

Proof Clearly,we only need to prove the necessity.First we give a key technique.Suppose that A1,A2,···,Anand T are in A such thatThen for all S1,S2∈A,we have

and

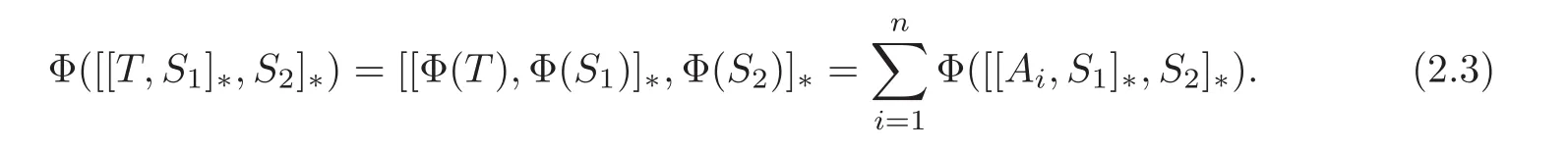
In the following,we will complete the proof of Theorem 2.1 by proving several claims.

Claim 1 Φ(0)=0.

Since Φ is surjective,there exists A ∈ A such that Φ(A)=0.Then we obtain Φ(0)=Φ([[0,A]∗,A]∗)=[[Φ(0),Φ(A)]∗,Φ(A)]∗=0.

Claim 2 Φ(RI)=RI, Φ(CI)=CI and Φ preserves self-adjoint elements in both directions.

Let λ ∈ R be arbitrary.Since Φ is surjective,there exists B ∈ A such that Φ(B)=I.By Claim 1,we have that

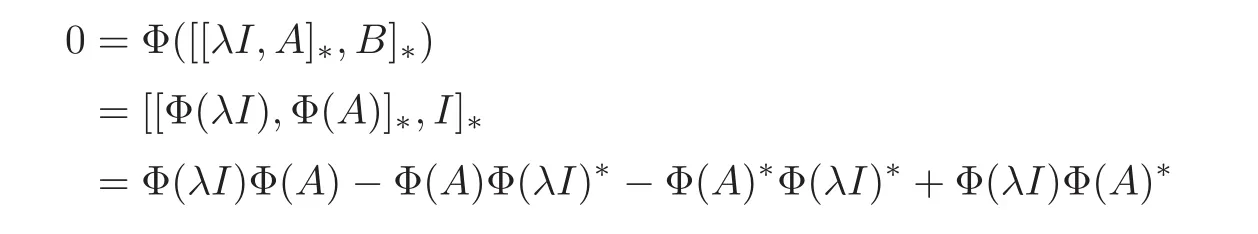
holds true for all A∈A.That is,

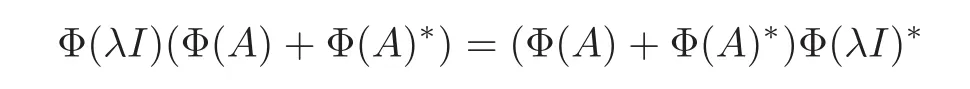
holds true for all A∈A.So

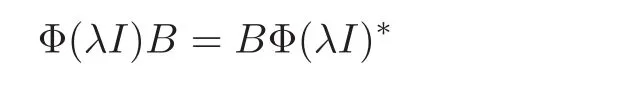
holds true for all B=B∗∈B.Since for every B ∈B,B=B1+iB2withandit follows that

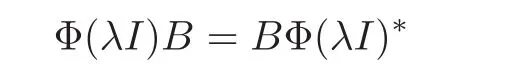
holds true for all B ∈ B.It follows from Lemma 2.1 that Φ(λI) ∈ RI.Note that Φ−1has the same properties as Φ.Similarly,if Φ(A)∈ RI,then A ∈ RI.Therefore,Φ(RI)=RI.

Let A=A∗∈ A.Since Φ(RI)=RI,there exists λ ∈ R such that Φ(λI)=I.Then

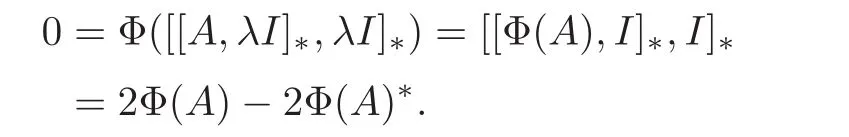
Hence Φ(A)= Φ(A)∗.Similarly,if Φ(A)= Φ(A)∗,then A=A∗∈ A.Therefore Φ preserves self-adjoint elements in both directions.

Let λ ∈ C be arbitrary.For every A=A∗∈ A,we obtain that

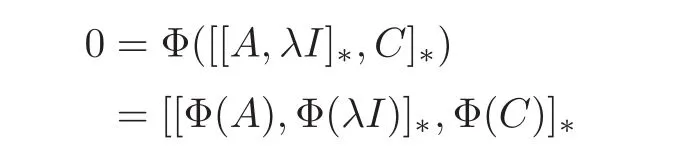
holds true for all C∈A.It follows from Lemma 2.1 that

Since A=A∗,we have Φ(A)= Φ(A)∗.Hence

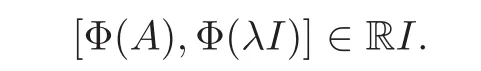
It follows from Lemma 2.2 that

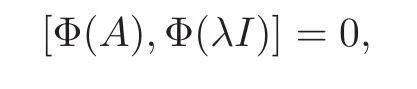
and then

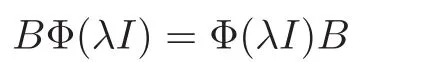
for all B=B∗∈B.Thus for every B ∈B,since B=B1+iB2withandwe get

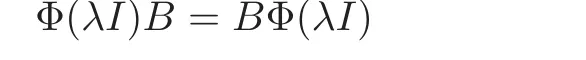
holds true for all B ∈ B.Hence Φ(λI)∈ CI.Similarly,if Φ(A)∈ CI,then A ∈ CI.Therefore,Φ(CI)=CI.

By Claim 2,we have

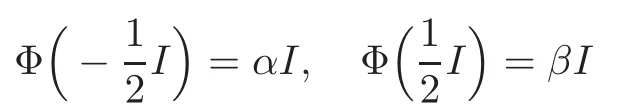
and

where α,β,γ,ω,γ1,ω1∈ R and αβγω 6=0.It follows fromthat

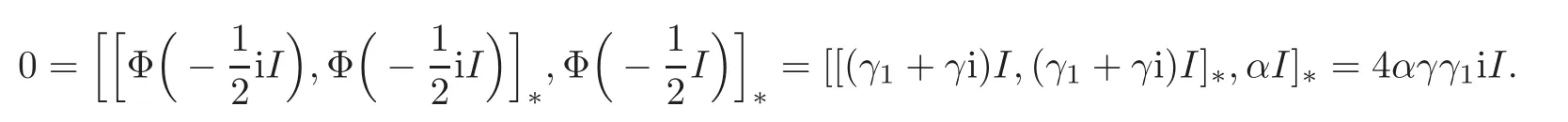
So γ1=0.Similarly,by the equalitywe get that ω1=0.

Now we get

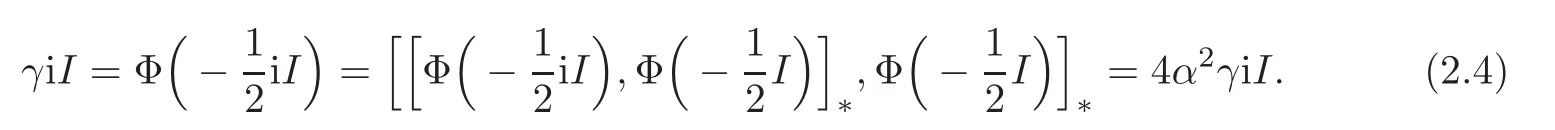
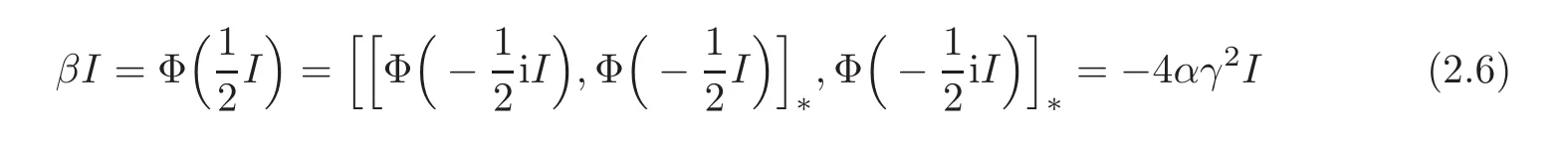
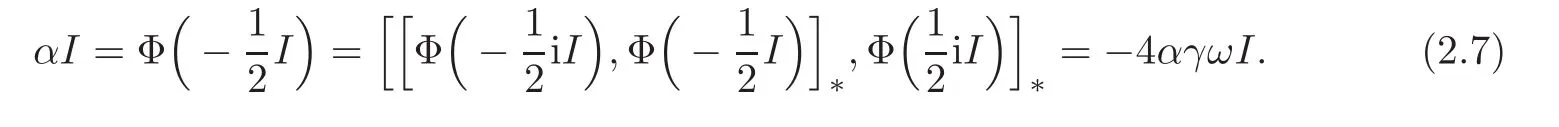
Now(2.4)–(2.7)ensures that

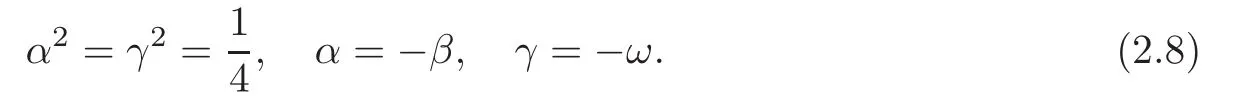
For every A∈A,it follows from iAthat

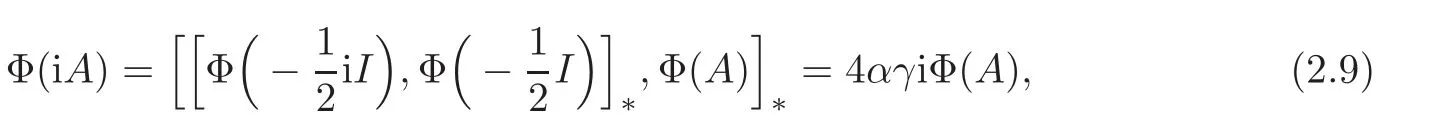
which together with(2.8)implies that Φ(iA)=iΦ(A)(∀A ∈ A)or Φ(iA)= −iΦ(A)(∀A ∈ A).

Choose an arbitrary nontrivial projection P1∈A,and write P2=I−P1.Denote Aij=PiAPj,i,j=1,2,then.For every A∈A,we may writeIn all that follows,when we write Aij,it indicates that Aij∈ Aij.The following Claims 4–9 are devoted to the additivity of Φ.

Claim 4 For every A11∈A11and B22∈A22,we have

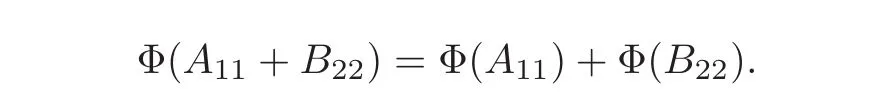
Since Φ is surjective,we may find an elementsuch that

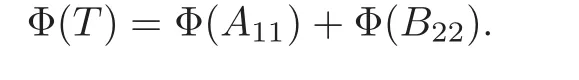
Since[[iP1,I]∗,A22]∗=0,it follows from(2.1)and Claim 1 that

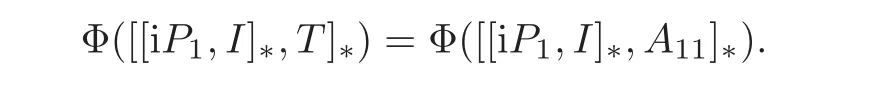
By the injectivity of Φ,we obtain that

and then we get T11=A11,T12=T21=0.Similarly,T22=B22,proving the claim.

Claim 5 For every A12∈A12,B21∈A21,we have

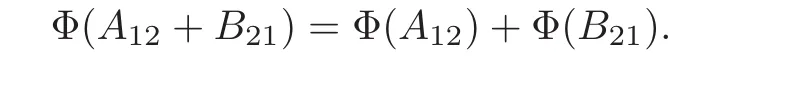
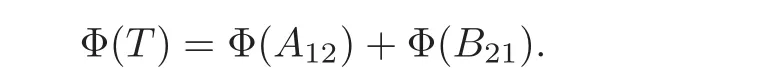
Since

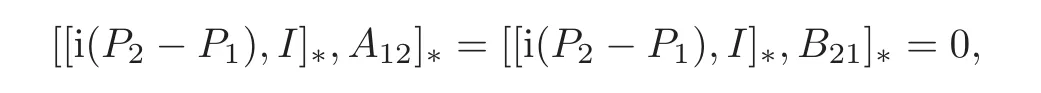
it follows from(2.1)that

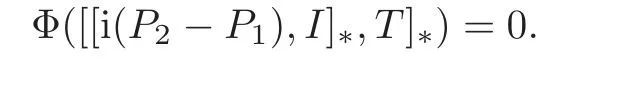
From this,we get[[i(P2− P1),I]∗,T]∗=0.So T11=T22=0.Since[[A12,P1]∗,I]∗=0,it follows from(2.3)that

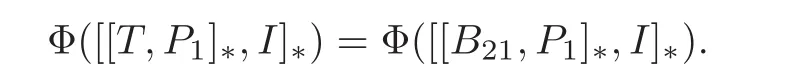
By the injectivity of Φ,we obtain that

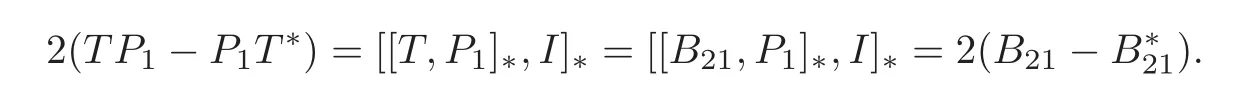
Hence T21=B21.Similarly,T12=A12,proving the claim.

Claim 6 For every A11∈A11,B12∈A12,C21∈A21,D22∈A22,we have

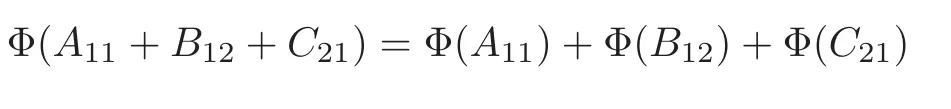
and

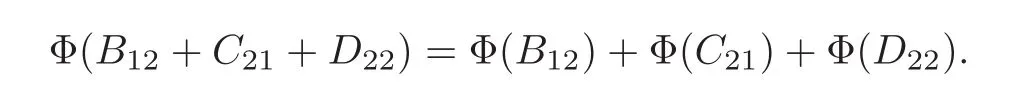
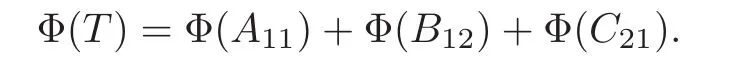
It follows from(2.1)and Claim 5 that

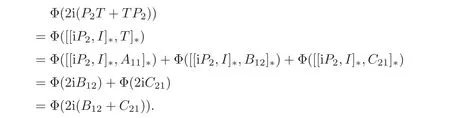
Thus P2T+TP2=B12+C21,which implies T22=0,T12=B12,T21=C21.Now we get T=T11+B12+C21.

Since

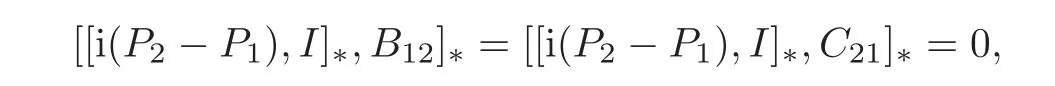
it follows from(2.1)that

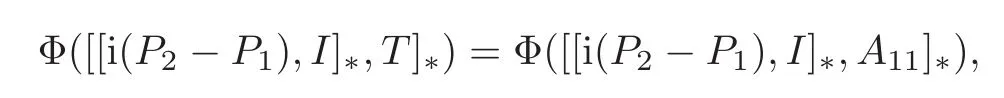
from which we get T11=A11.Consequently,Φ(A11+B12+C21)=Φ(A11)+Φ(B12)+Φ(C21).

Similarly,we can get that Φ(B12+C21+D22)= Φ(B12)+Φ(C21)+Φ(D22).

Claim 7 For every A11∈A11,B12∈A12,C21∈A21,D22∈A22,we have

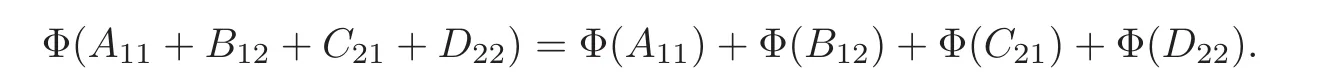
It follows from(2.1)and Claim 6 that

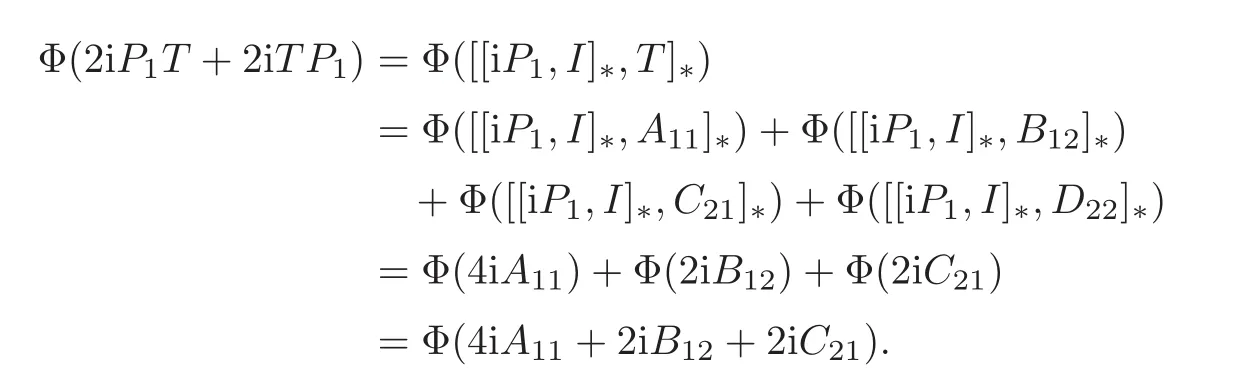
Thus

it follows that T11=A11,T12=B12,T21=C21.Similarly,we can get

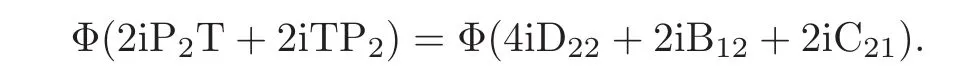
From this,we get T22=D22,proving the claim.

Claim 8 For every Ajk,Bjk∈Ajk,1≤j 6=k≤2,we have

Since

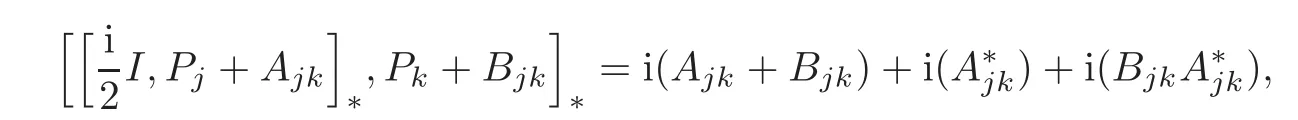
we get from Claim 7 that

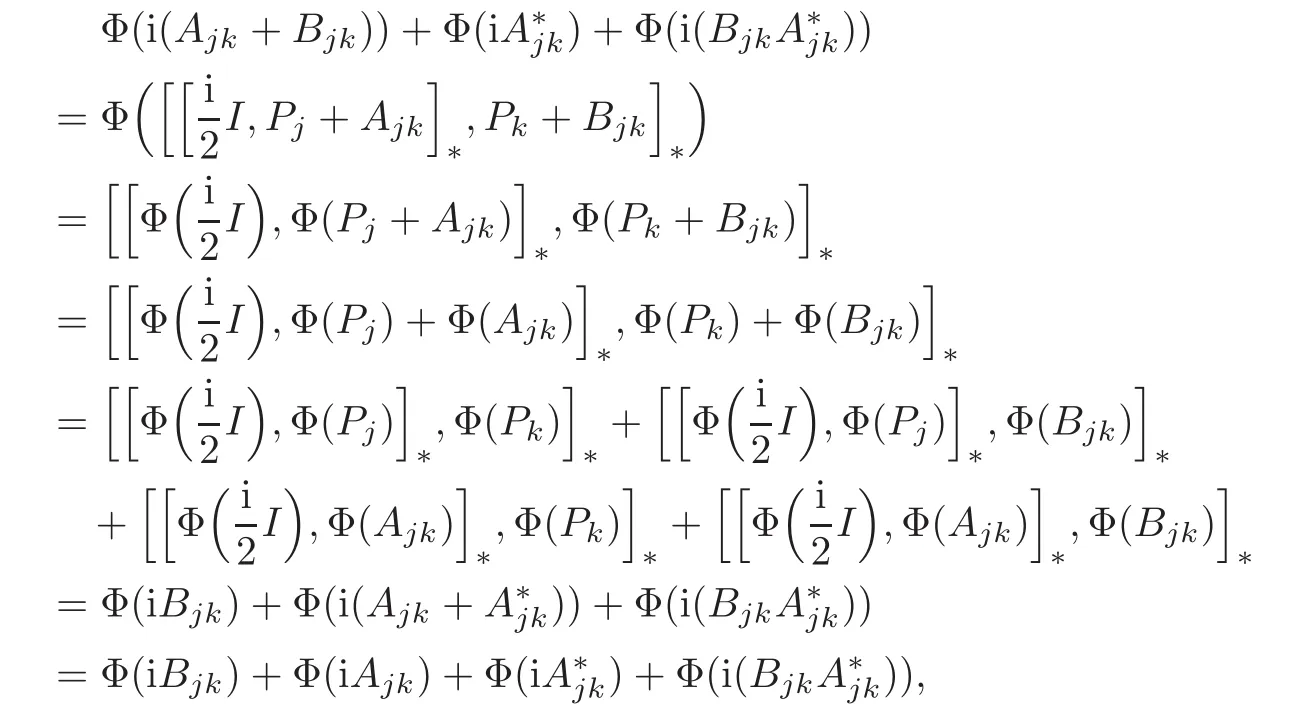
which implies Φ(i(Ajk+Bjk))= Φ(iBjk)+Φ(iAjk).By Claim 3,we obtain that Φ(Ajk+Bjk)=Φ(Ajk)+Φ(Bjk).

Claim 9 For every Ajj∈Ajjand Bjj∈Ajj,1≤j≤2,we have

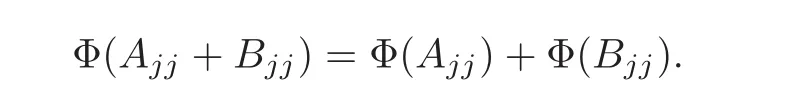
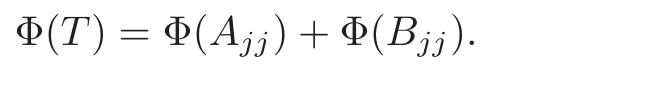
For 1≤j 6=k≤2,it follows from(2.1)that

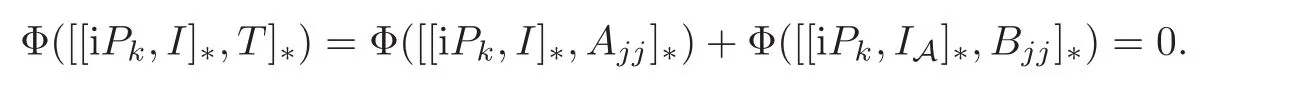
Hence PkT+TPk=0,which implies Tjk=Tkj=Tkk=0.Now we get T=Tjj.

For every Cjk∈Ajk,j 6=k,it follows from(2.2)and Claim 8 that

Hence

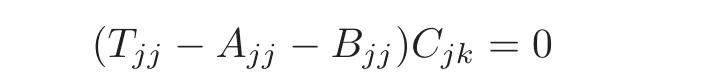
for all Cjk∈Ajk.By the primeness of A,we get that Tjj=Ajj+Bjj,proving the claim.

Claim 10 Φ is ∗-additive.

The additivity of Φ is an immediate consequence of Claims 7–9.For every A ∈ A,A=A1+iA2,whereare self-adjoint elements.By Claims 2–3,if for every A ∈ A,Φ(iA)=iΦ(A),then

Similarly,if Φ(iA)= −iΦ(A)(∀A ∈ A),we also have Φ(A∗)= Φ(A)∗.

By Claims 3 and 10,we get that Φ(I)=I or Φ(I)= −I.In the rest of this section,we deal with these two cases respectively.

Case 1 If Φ(I)=I,then Φ is either a linear ∗-isomorphism or a conjugate linear ∗-isomorphism.

If Φ(I)=I,by(2.8)–(2.9)and Claim 10,thenΦ(iI)=2ωiI and Φ(iA)=−2γiΦ(A)for all A∈A.For all A,B ∈ A,we can obtain that

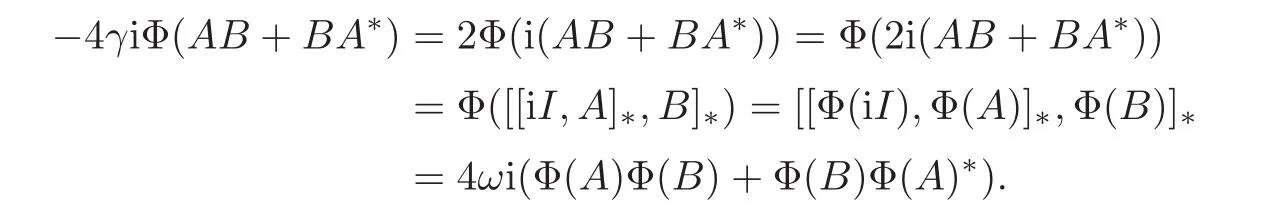
From this,we get

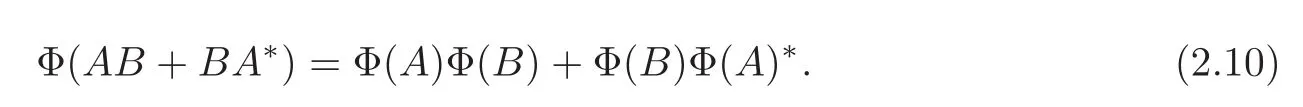
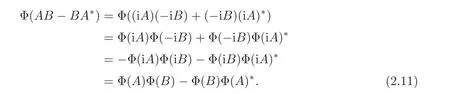
For all A,B∈A,it follows from Claim 3 that Summing(2.10)with(2.11),we get that Φ(AB)= Φ(A)Φ(B).

For every rational number q,we have Φ(qI)=qI.Indeed,since q is a rational number,there exist two integers r and s such that q=Since Φ(I)=I and Φ is additive,we get that

Let A be a positive element in A.Then A=B2for some self-adjoint element B∈A.It follows from Claim 11 that Φ(A)= Φ(B)2.By Claim 2,we get that Φ(B)is self-adjoint.So Φ(A)is positive.This shows that Φ preserves positive elements.

Let λ∈R.Choose sequence{an}and{bn}of rational numbers such that an≤λ≤bnfor all n andIt follows from

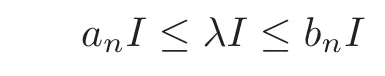
that

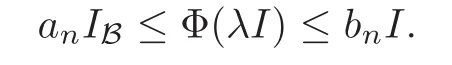
Taking the limit,we get that Φ(λIA)= λIB.Hence for all A ∈ A,

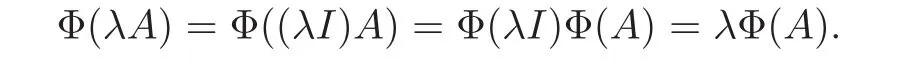
Hence Φ is real linear.Therefore,if Φ(iA)=iΦ(A)(∀A ∈ A),then Φ is a linear ∗-isomorphism.If Φ(iA)= −iΦ(A)(∀A ∈ A),then Φ is a conjugate linear ∗-isomorphism.

Case 2 If Φ(I)= −I,then Φ is either the negative of a linear∗-isomorphism or the negative of a conjugate linear∗-isomorphism.

Consider that the map Ψ :A → B defined by Ψ(A)= −Φ(A)for all A ∈ A.It is easy to see that Ψ satisfies Ψ([[A,B]∗,C]∗)=[[Ψ(A),Ψ(B)]∗,Ψ(C)]∗for all A,B,C ∈ A and Ψ(I)=I.Then the arguments for Case 1 ensure that Ψ is either a linear ∗-isomorphism or a conjugate linear ∗-isomorphism.So Φ is either the negative of a linear ∗-isomorphism or the negative of a conjugate linear∗-isomorphism.

Combining Cases 1–2,the proof of Theorem 2.1 is finished.

AcknowledgementThe authors would like to thank the referee for his valuable comments and suggestions.