自锚式梁下斜张简支桥梁破坏模式试验与数值研究

陈孜伟， 陈德伟， 白植舟

(同济大学 土木工程学院， 上海 200092)

自锚式梁下斜张桥梁是一种非常规的预应力桥梁[1]，通常由主梁、竖向撑杆和斜张系统3部分构成[2-4].斜张索张拉后其竖向分力可以大幅度消除恒载作用下的主梁弯矩，同时其对主梁的轴向会产生压应力储备，提高主梁的极限抗弯承载能力.

斜张索及撑杆能减轻结构自重产生的弯矩，可取消施工支架，在建筑高度较高且难以搭设支架的地区，如较宽的河道和山谷，其应用具有较大优势.Muttoni[5]研究了撑杆数量对活载作用下主梁弯矩的影响.Ruiz-Teran等[6-7]对车载作用下突发索断的梁下斜张桥的动力放大系数及结构内力响应进行了研究.Camara等[8]对地震激励下的梁下斜张索对结构动力响应的削减作用进行了研究.Camara等[9]对考虑了重车轮胎尺寸、路面粗糙程度及横坡的梁下斜张薄板梁的车桥耦合进行了研究.

虽然该类桥梁在国外已经有了一定的应用，但对其破坏模式和机理的研究，鲜见报道.梁下体外预应力将会对主梁产生轴向压力，且轴向压力随荷载变化而变化，导致其破坏机理具有一定的复杂性.为探讨该类结构的破坏模式和机理，本文以梁下斜张简支梁为研究对象，基于模型试验和ANSYS精细化有限元模型分析方法，对其破坏模式和机理进行研究，并对影响结构破坏模式的参数进行分析，得出了有益的结论.

1 试验模型

将计算跨径为10 m的简支梁下斜张桥梁作为研究对象.根据设计经验[3]，取梁高为0.333 m，撑杆高度为1.548 m，主梁高跨比为1/30，撑杆高跨比为3/20，模型标准截面为工字型截面，如图1a所示.

主梁采用C70自密实混凝土，重度22 kN·m-3，杨氏弹性模量3.90×104MPa，轴心抗压强度49.72 MPa.纵向普通钢筋配筋率为0.7%，箍筋体积配筋率为1.03%，均采用直径为6mm的HRB500螺纹钢筋.竖向撑杆采用Q345钢材.体内和体外预应力束均采用1Φs15.2钢绞线，其屈服强度为1 920 MPa，其中顶板4束、腹板1束、底板2束，斜张索2束.采用后张法两端张拉，在锚固端设置拉压传感器控制其张拉力.采用刚性支撑连续梁法确定初始斜张索力，得出成桥初始索力为55.00 kN，为屈服索力的20.46%，成桥初始状态下主梁的最大正应力为6.81 MPa(图1中的M点，压应力为正)，发生在距离跨中2.32 m的底板处，如图1a所示.

模型试件主梁共布置30个Bx20-3AA应变计，其中于1/3跨和2/3跨支座侧顶板混凝土表面各贴3个，于跨中、1/3跨和2/3跨的顶、底板纵向钢筋各绑8个；并在主梁1/4跨、3/4跨、1/3跨及2/3跨分别设置NS-WY06位移计，在梁端和跨中撑杆下方设置拉杆位移计，如图1a所示.

a 结构立面图及断面图(单位:mm)b 试件照片

图1模型试件

Fig.1Testmodel

主梁养护28 d并完成体内、外预应力束张拉后，使用YC-60型千斤顶对主梁跨中开始逐级加载，并用3816采集仪采集加载过程中的荷载、位移和应变，直至跨中集中荷载达到386.00 kN.此时梁下斜张索拉应力监测达到1 806.00 MPa(已接近屈服应力1 920.00 MPa)，终止继续增大跨中集中荷载，并记录裂缝.

加载过程中，当跨中集中荷载增长至90.12 kN时，主梁1/3截面底板首先出现明显的贯穿底板的横向裂缝，如图2a所示；随着荷载的继续增大，裂缝延伸到下翼缘板外侧，如图2b所示；之后1/3跨断面～1/4跨断面间底板继续出现横向裂缝，但并没有贯穿桥面板，如图2c所示.

a 底板b 下翼缘c 1/3跨～1/4跨

图21/3跨裂缝

Fig.2Cracksin1/3span

2 有限元计算及破坏机理分析

考虑对称性，采用ANSYS软件建立试验梁的半梁有限元模型，如图3所示，对其进行数值模拟.主梁混凝土考虑开裂采用solid65单元模拟，普通钢筋以及预应力束采用实体力筋法，用link180单元模拟，其中，体内预应力束以及梁下斜张索采用初应变作为施加预应力的方式.钢材的本构关系采用理想弹塑性模型；混凝土的压应力-应变关系采用抛物线上升段和直线段模型;拉应力-应变关系采用单直线模型.全结构共计4 509个节点，3 877个单元(其中实体单元2 954个，空间杆单元923个).跨中集中荷载按照模型试验中千斤顶钢垫板规格采用0.2 m×0.4 m的面荷载加载，每个荷载步加载的荷载值为30 kN.

图3 ANSYS有限元计算模型

2.1 理论分析与试验结果对比

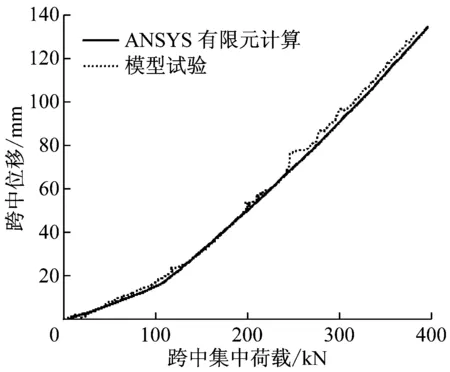
对比了试验与ANSYS有限元计算结果，分别以跨中位移及梁下斜张索索力随跨中集中荷载的变化规律为研究对象，如图4所示，得出以下结论：

(1)模型试验终止时跨中集中荷载为386.00 kN，跨中位移为13.3 cm，ANSYS有限元计算模型跨中位移为12.2 cm(396.00 kN时，最大位移为13.5 cm)，如图4a所示.模型试验的力-位移曲线与ANSYS有限元计算结果基本吻合.模型试验和ANSYS有限元计算的力-位移曲线在跨中集中荷载为90.00 kN时有斜率变化，跨中集中荷载为108.00 kN时斜率变化更为明显.

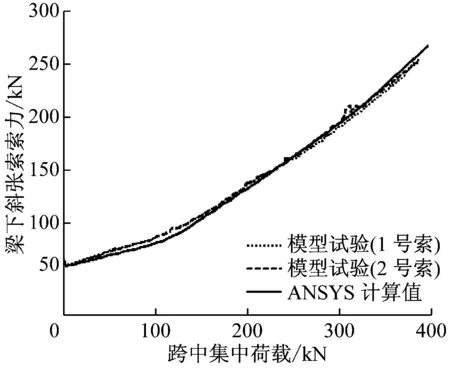
(2)试验终止时两束索的索力分别为252.90 kN和252.52 kN，而ANSYS有限元计算值为257.24 kN(396.00 kN时，最大索力为265.51 kN)，如图4b所示，两者斜张索的力-索力曲线基本吻合.当跨中集中荷载达到90.00 kN以后，斜张索的索力随集中荷载的变化率开始增大.

模型试验结果和ANSYS有限元计算结果表明，当外荷载达到模型试验的最大值386.00 kN时，两者索拉应力分别达到1 806.42 MPa和1 837.43 MPa，已经接近其屈服应力1 920.00 MPa.此时，主梁1/3跨和2/3跨临界断面顶板最大压应变测量值分别为4.88×10-4和4.84×10-4，计算值为4.90×10-4(混凝土压应变为正)，低于峰值应变值0.002和极限应变值0.003，如图5所示，混凝土计算压应力为19.10 MPa.测量和计算均表明，该处底板纵向抗拉钢筋屈服(500.00 MPa)，而顶板抗压钢筋未屈服(达-100.40 MPa)，如图6所示(钢筋拉应力为正).理论计算与试验测量结果相符.

a 力-位移曲线

b 力-索力曲线

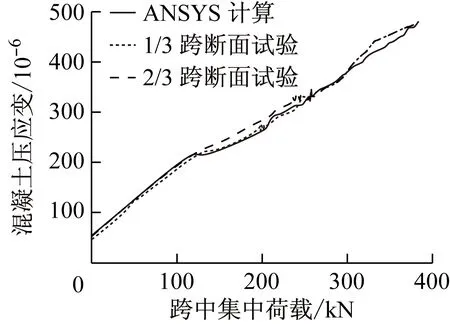
图5 1/3跨临界断面顶板混凝土的荷载-应变曲线

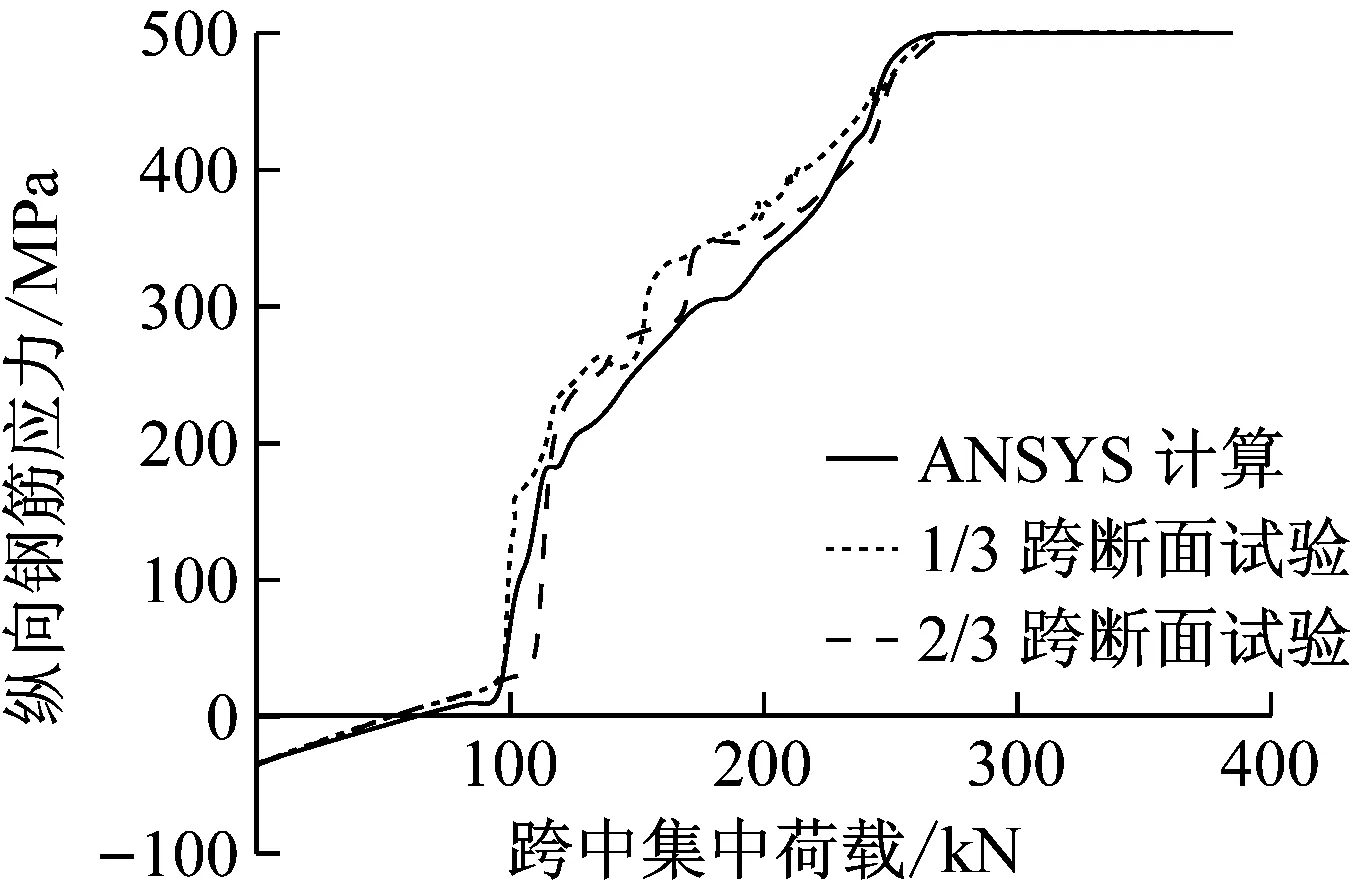
a 抗拉钢筋

b 抗压钢筋

试验测量与理论计算结果均表明，试验梁破坏模式为斜张索断裂先于主梁混凝土压溃.此时，索力的轴向分力对主梁工字型断面的轴向压应力由初始的0.43 MPa增大到3.02 MPa.

2.2 结构效率值

定义结构效率值φ为外荷载作用下，由梁下斜张索系统导致的弯矩卸载量与无斜张系统的弯矩的比值[10-11].在弹性阶段，对本文模型试件跨中作用集中荷载Q时，结构效率值φ的解析表达式[10-11]为

(3)

式(1)～(3)中:Ec为主梁混凝土弹性模量；Ic为主梁惯矩；E为斜张索弹性模量；Asc为斜张索截面面积；L为简支梁跨径；Ac为主梁截面面积；α为主梁轴线与斜张索轴线夹角.表1列出了模型试件在跨中集中荷载作用下的各内力与外荷载和结构效率值φ的数学关系.

图7给出了模型试件结构效率值φ与跨中荷载Q的关系.结果表明，结构效率值φ随着加载的进行由弹性阶段的0.26增长至0.90，即随着混凝土开裂，主梁的抗弯刚度降低，斜张索承担的内力比例迅速提升，索力对主梁的轴向压应力增大，而其竖向分力极大地削减了主梁的荷载弯矩.

表1 模型试件内力与结构效率值φ的解析关系

图7 荷载与结构效率值曲线

2.3 破坏机理分析

由试验与ANSYS分析可知，主梁临界断面为1/3跨断面，主梁将最先在1/3跨断面发生破坏(混凝土压应变最大).

针对每个荷载步，将斜张索索力等效为轴向分力和跨中竖向分力，作用于模型主梁的简支梁，计算在逐级增大的跨中集中荷载作用下，1/3跨断面(临界断面)处的极限抗弯承载能力，以其作为梁下斜张梁的抵抗弯矩，并与该荷载步下梁下斜张梁的荷载弯矩进行对比，如图8所示.

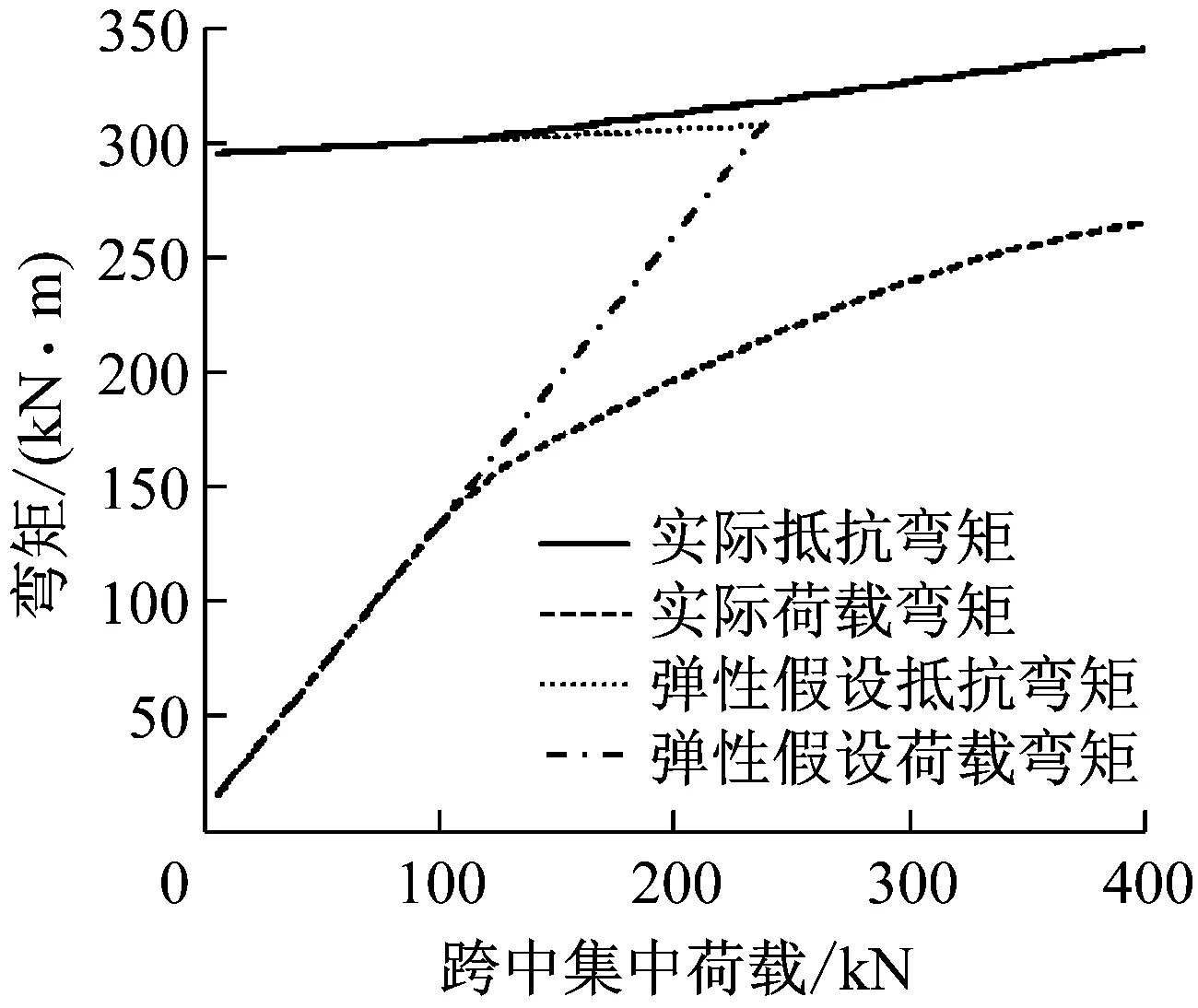
图8 荷载与1/3跨临界断面弯矩

由图8可知，主梁1/3跨断面的荷载弯矩随跨中集中荷载的增加而增大，同时该断面的抵抗弯矩也随外荷载增大.如2.2中所述，随着混凝土开裂和结构效率值φ的提升，索力竖向分力削减了主梁的荷载弯矩，使其随外荷载增长的斜率降低；索力轴向分力增大了主梁的压应力储备，使抵抗弯矩及其变化斜率均随外荷载增大.在加载后期，主梁抵抗弯矩的增长比其荷载弯矩增长得快，直至斜张索断裂，该两条荷载-弯矩曲线仍不能相交，因此试验梁的破坏模式为斜张索断裂先于主梁混凝土压溃.假设结构始终处于弹性状态，即不考虑混凝土开裂，因此结构效率值在加载中保持初始值不变，主梁临界断面的抵抗弯矩和荷载弯矩增长斜率不随外荷载变化，由图8不难得出，结构的破坏模式为主梁混凝土压溃先于斜张索断裂，结构所能承受的最大跨中集中荷载为240.00 kN，远低于实际值396.00 kN，因此弹性假设下的结构受力状态偏于保守.

3 参数分析

为研究结构效率值φ对跨中集中荷载作用下梁下斜张桥破坏模式的影响规律，以试验试件为基础，分别单独调整与结构效率值φ相关的斜张索截面面积和撑杆高跨比，获得调整后结构的破坏模式并进行极限承载能力分析.

3.1 斜张索截面面积对破坏模式的影响

为研究斜张索截面面积对结构破坏模式的影响，通过已经建立的ANSYS有限元模型，调整模型中斜张索面积(初始总索力仍为110.00 kN)进行数值分析.计算获得结构破坏时主梁1/3跨断面(临界断面)的最大荷载弯矩和最大抵抗弯矩，以及加载过程中外荷载与结构效率值φ之间的关系，如图9所示，得出以下结论：

(1)斜张索截面面积由0.25Asc增至1.50Asc(Asc=280 mm2)，结构的破坏模式为斜张索断裂先于主梁压溃，结构所能承受的最大跨中荷载以及主梁的最大抵抗弯矩和最大荷载弯矩均随索面积增大；索面积为1.75Asc时，结构的破坏模式为主梁先压溃而斜张索未屈服.

(2)随着索面积的增大，主梁开裂时的跨中荷载增大.主梁进入塑性后，结构效率值第1个增长区间的斜率随索面积的增大而降低，第1个增长区间与第2个增长区间的拐点(裂缝数量稳定)对应的结构效率值随之增大.其中，索面积为0.25Asc的算例中，结构效率值未达到拐点斜张索就已断裂；索面积为1.75Asc的算例中，因结构效率值增长斜率较低，索力对主梁抵抗弯矩的增强和荷载弯矩的削减作用不明显，所以产生了主梁压溃先于斜张索屈服的破坏模式.

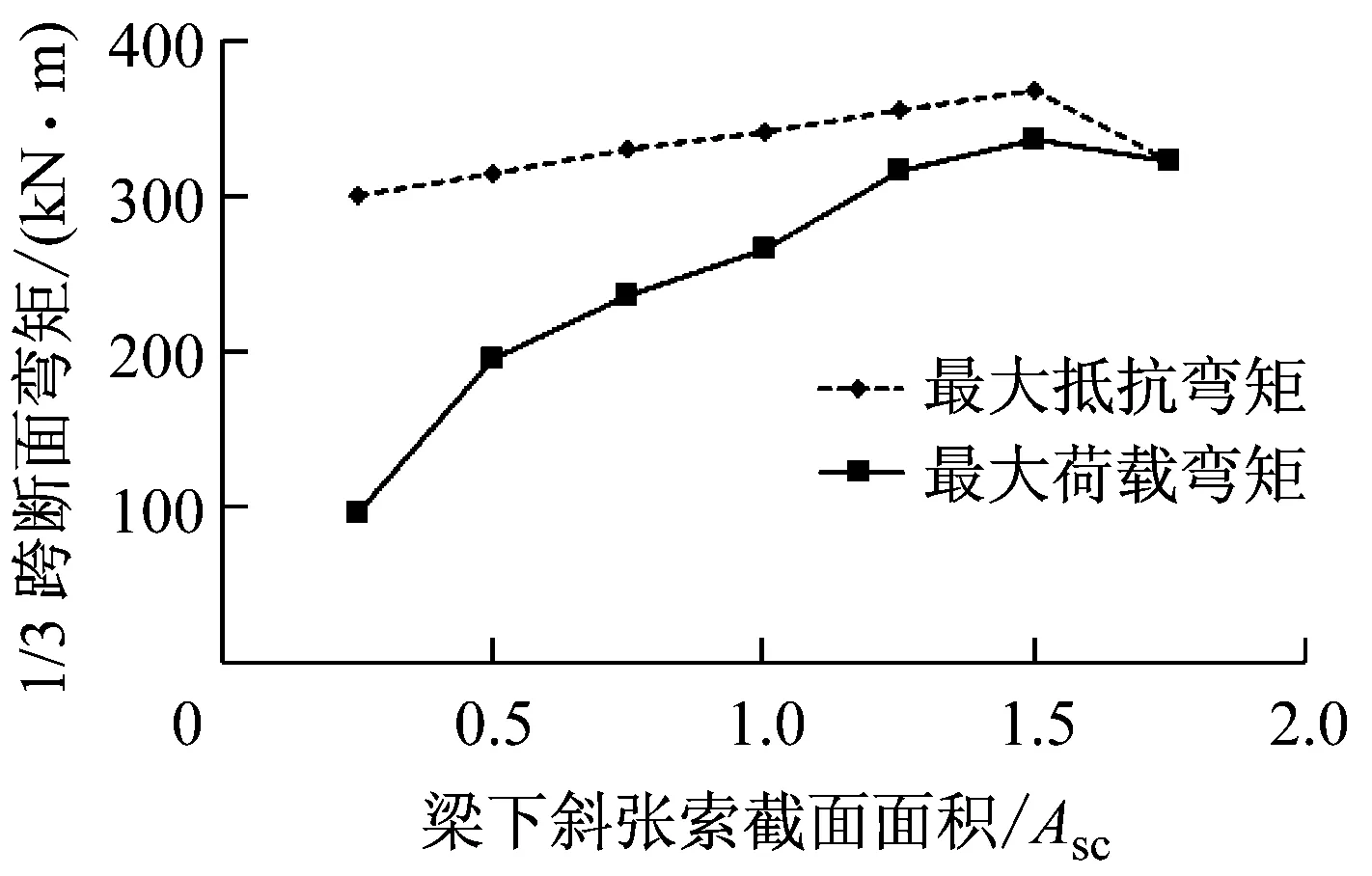
a 索截面面积与临界断面弯矩关系

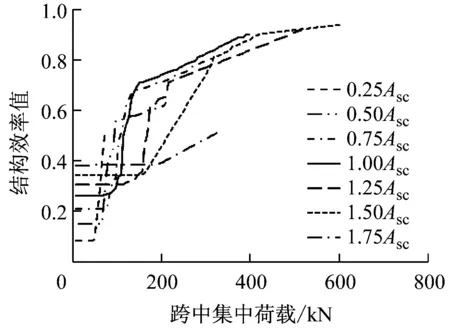
b 荷载与结构效率值曲线

Fig.9Parameteranalysisaimingatfailuremodesofstructureswithdifferentcablesectionareas

分析显示，自锚式梁下斜张桥梁破坏模式和斜张索截面Asc相关，当Asc面积相对较大时，将产生主梁先压溃的破坏模式，反之，则为斜拉索先断裂的破坏模式.

3.2 撑杆高跨比H/L对破坏模式的影响

为研究撑杆高跨比H/L对结构破坏模式的影响，通过已经建立的ANSYS有限元模型，调整模型中撑杆高跨比进行数值分析.采用刚性支承连续梁法确定其初始索张拉力，即确保总索力的竖向分力均为64.24 kN.计算获得结构破坏时主梁1/3跨断面(临界断面)的最大荷载弯矩和最大抵抗弯矩，以及加载过程中外荷载与结构效率值φ之间的关系，如图10所示，得出以下结论：

(1)当撑杆高跨比为0.03(即α=3.43°，梁下斜张索在结构中的作用已接近体内预应力束)时，初始总索力即为屈服索力537.60 kN，开始加载后，斜张索将立即屈服.

(2)撑杆高跨比由0.15增至0.30的算例中，结构的破坏模式为斜张索断裂先于主梁压溃，结构所能承受的最大跨中荷载随撑杆高跨比增大，主梁的最大抵抗弯矩和最大荷载弯矩均随撑杆高跨比增大而减小，前者减小得比后者缓慢；撑杆高跨比为0.05和0.10的算例中，结构的破坏模式为主梁先压溃而斜张索未屈服.

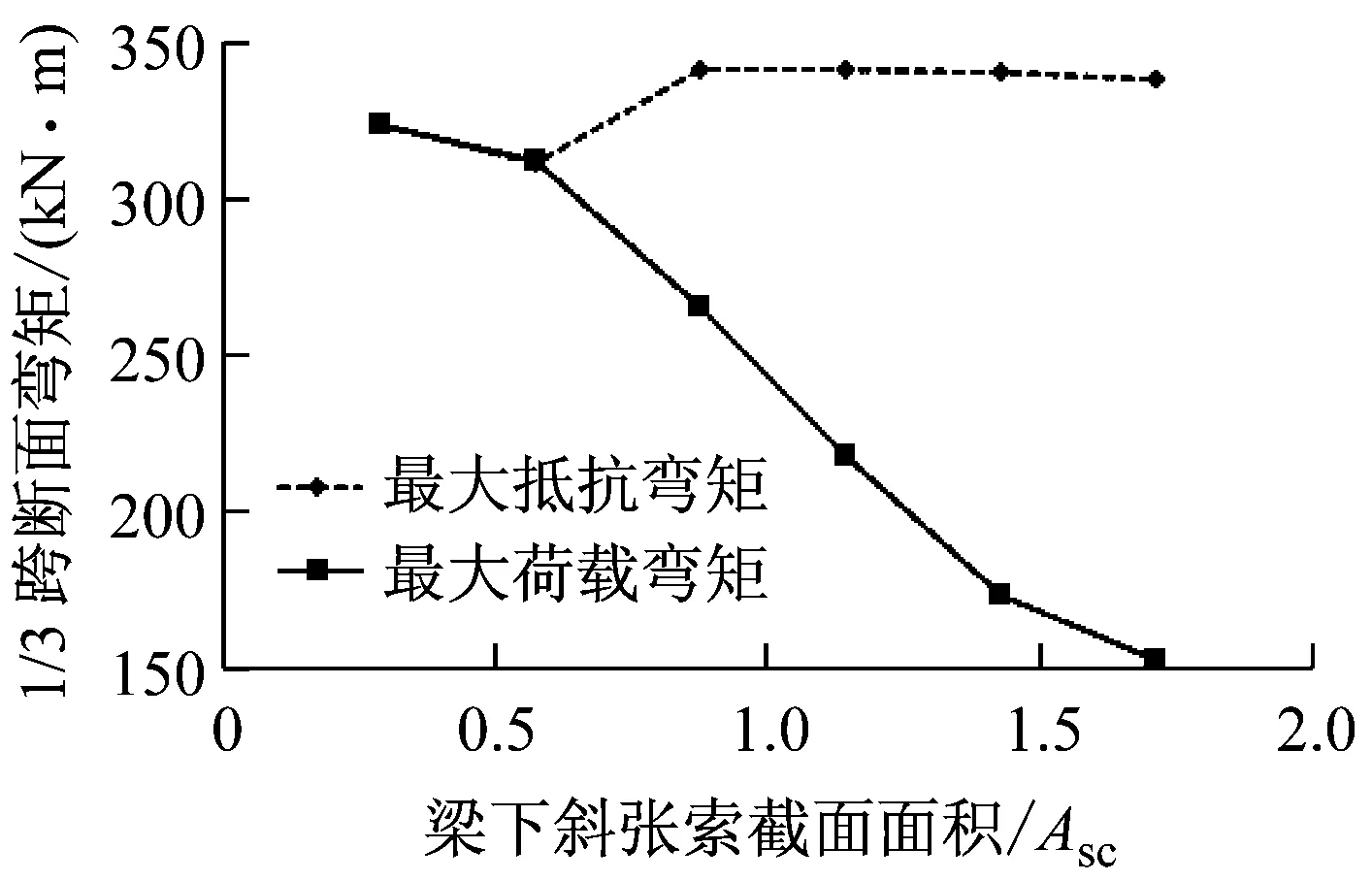
a 撑杆高跨比与临界断面弯矩关系

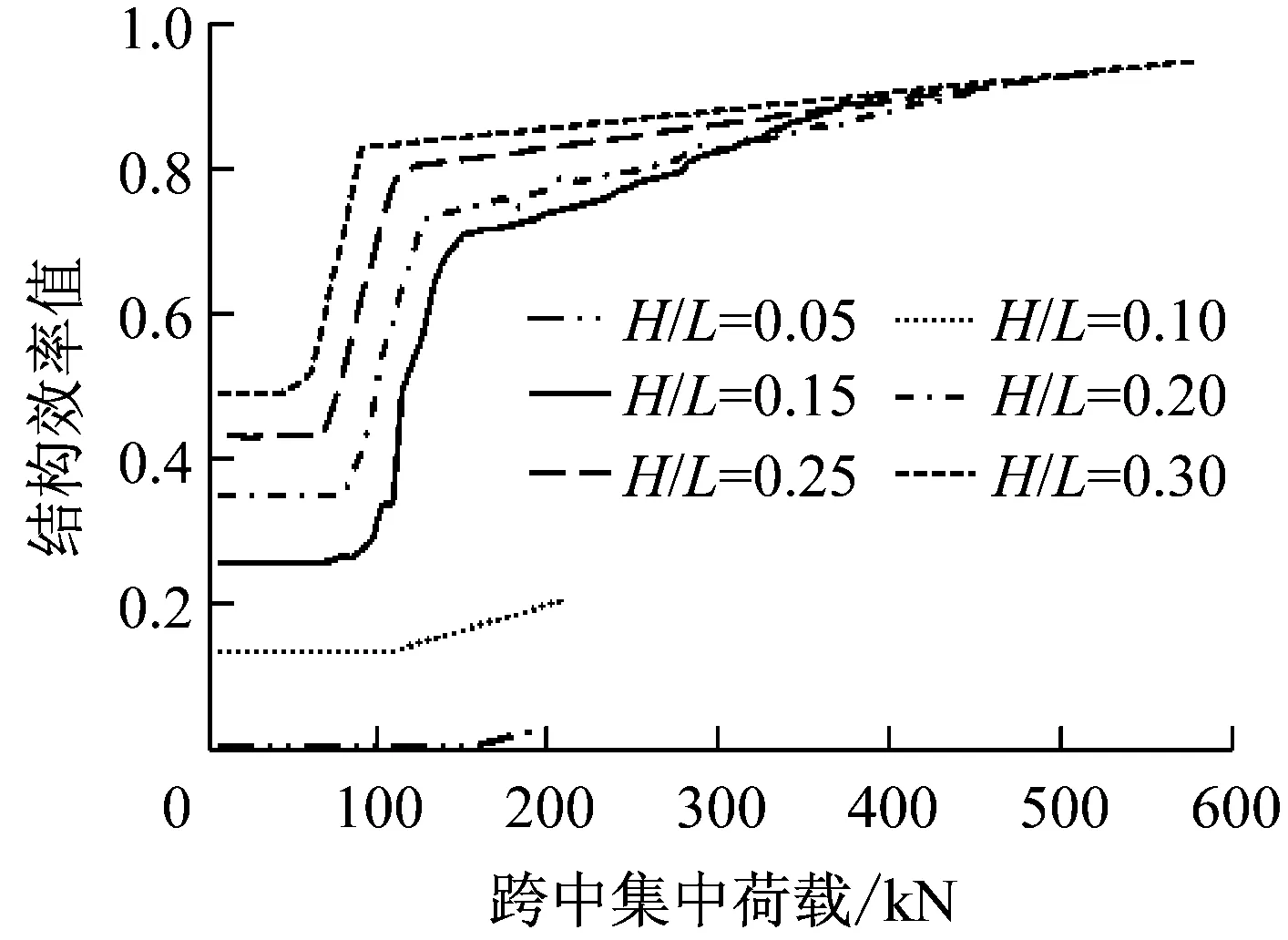
b 荷载与结构效率值曲线

Fig.10Parameteranalysisaimingatfailuremodesofstructureswithdifferentdepth-spanratiosofstrut

(3)随着撑杆高跨比的增大，主梁开裂时的跨中荷载降低.主梁进入塑性后，结构效率值第1个增长区间的斜率随撑杆高跨比的增大而增大，第1个增长区间与第2个增长区间拐点对应的结构效率值也随之增大.其中，撑杆高跨比为0.05和0.30的算例中，由于结构的初始效率值较低，且结构效率值增长斜率较低，索力对主梁抵抗弯矩的增强和荷载弯矩的削减作用不明显，所以产生了主梁压溃先于斜张索断裂的破坏模式.

分析显示，自锚式梁下斜张桥梁破坏模式和撑杆高跨比H/L相关，当撑杆高跨比H/L相对较小时，将产生主梁先压溃的破坏模式；反之，则为斜拉索先断裂的破坏模式.

4 板式主梁结构对比分析

由公式(1)～(3)可知，增大主梁的长细比可以提升结构效率值，可以通过采用梁高较低的板式主梁实现[10-11].在跨中集中荷载作用下，主梁截面采用高0.167 m、宽0.666 m的板梁截面，主梁内部普通钢筋仍采用直径6 mm的HRB500螺纹钢筋(上、下两侧各6根)，而体内预应力束采用2束4Φs15.2的通长直束，分别位于主梁形心轴的左右两侧.板式主梁结构的混凝土用量为模型试件的70.92%，体内预应力束用量比模型试件多38.81%，梁下斜张索与模型试件相同，板式主梁结构的材料成本低于工字型梁结构.根据刚性支撑连续梁法，斜张索的初始张拉应力为75.30 MPa，在斜张索初张力、体内束预张力和自重的共同作用下，在成桥初始状态主梁内部可达到全截面受压的应力状态，最大正应力为8.48 MPa.

计算结果表明，板式结构的极限跨中荷载为378.00 kN，基本与试验梁接近，其破坏模式同样为斜张索断裂先于主梁压溃.破坏时主梁跨中混凝土压应变达到最大值0.000 67，低于极限峰压应变值0.002 00.

板式主梁结构的跨中集中荷载作用下的荷载-结构效率值曲线如图11所示.对比图11与图7可知，板式主梁初始结构效率值远高于工字型主梁；前者的结构效率值在主梁开裂后的第1个增长区间增长得比后者缓慢；前者在第1个增长区间和第2个增长区间的拐点(裂缝数量稳定)对应的结构效率值大于后者.

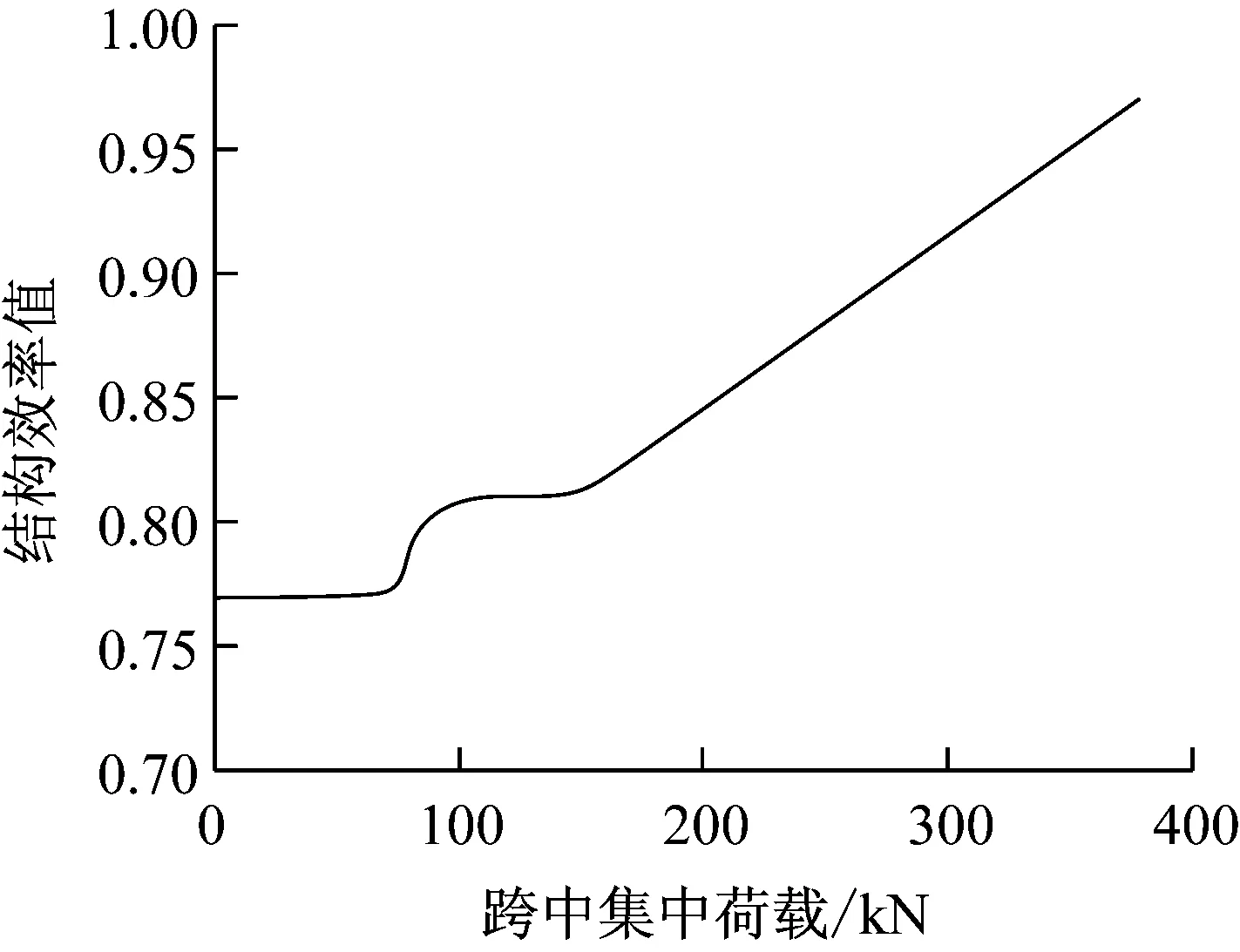
图11 板式主梁结构的荷载与结构效率值曲线

板式主梁弹性假设与实际抵抗弯矩和荷载弯矩随跨中荷载的增长规律如图12所示.可以得出以下结论：

(1)跨中断面的抵抗弯矩在整个加载过程中都大于对应断面的荷载弯矩，其破坏模式与破坏机理与试验梁相同.在弹性假设下，结构的破坏模式为主梁混凝土压溃先于斜张索断裂，结构所能承受的最大跨中集中荷载为270.60 kN，低于实际值378.00 kN，弹性假设下的结构受力状态同样偏于保守.

(2)板式主梁的成桥初始正应力大于工字型主梁，且板梁结构的效率值在主梁进入塑性后增长得比工字型梁结构缓慢.因此，板式主梁1/3跨断面的抵抗弯矩随外荷载的增长曲线相较于工字型主梁更为平缓，而其荷载弯矩的增长曲线更加平滑，两者的增长斜率没有出现明显突变.

图12 跨中集中荷载与板梁结构主梁弯矩关系

Fig.12CurvesofQ-momentsinmidspanand1/3spanofstructurewithslabdeck

5 结论

对自锚式梁下斜张桥梁在逐级增大的跨中集中荷载作用下的结构反应机理进行了模型试验与ANSYS有限元分析研究，得到主梁临界断面的抵抗弯矩与荷载弯矩并进行比较，分析了产生试验模型破坏模式的原因，得出了以下主要结论：

(1)结构效率值φ决定了主梁和斜张索的内力分配关系.随着主梁混凝土进入塑性阶段，结构效率值φ提高，索力随外荷载的增长斜率提升，与索力轴向分力正相关的抵抗弯矩增长斜率提升，而与索力竖向分力负相关的荷载弯矩增长斜率降低.

(2)试验梁的破坏模式为斜张索断裂先于主梁压溃.在不考虑主梁开裂对结构效率值影响的弹性假设下，结构的破坏模式为主梁压溃先于斜张索断裂，所能承受的最大跨中荷载远低于实际值，根据弹性假设进行设计偏于保守.

(3)自锚式梁下斜张桥梁破坏模式和斜张索索面积与撑杆高跨比相关.当索面积相对较大或撑杆高跨比相对较小时，将产生主梁先压溃的破坏模式；反之，则为斜拉索先断裂的破坏模式.在通常的工程设计范围内，结构的破坏模式均为斜拉索先断裂的破坏模式.

(4)板式主梁结构的体内预应力束用量多于工字型梁结构，主梁混凝土用量低于工字型梁结构，材料成本低于工字型梁结构.其破坏模式仍为斜张索断裂先于主梁压溃，所能承受的最大跨中集中荷载略低于工字型主梁结构.