螺栓拼接钢梁的抗弯性能
童乐为, 牟晓亮, 周 锋, 龚 剑, 黄玉林, 王小安
(1. 同济大学 土木工程学院,上海 200092; 2. 上海建工集团股份有限公司, 上海 200080;3. 上海装配式建筑技术集成工程技术研究中心, 上海 200011)
近几十年来,随着超高层建筑施工技术的迅猛发展,我国陆续建成了一批超高层建筑,包括金茂大厦、广州西塔、上海环球金融中心、上海中心等[1].上海建工集团通过技术集成,研发出钢柱筒架交替支撑液压爬升整体钢平台模架装备系统(以下简称模架装备),并已成功应用于上海中心大厦、上海北外滩白玉兰广场和上海大中里综合发展项目T2主楼等重大工程项目的施工[2-5].
模架装备由钢平台、筒架支撑、工具式钢柱、脚手架、模板5大系统组成.其中,钢平台系统为模块化设计,采用标准化的钢梁截面和高强度螺栓连接方式,施工应用时可根据建筑几何尺寸需要,拼装钢平台,实现通用性.钢梁截面均为H型钢.为了满足各种几何尺寸的工程项目施工的需要和连接的方便,钢梁之间采用拼接板,通过高强度螺栓连接形成所需要的长度.在实际施工中,高强度螺栓连接处的构件表面不做专门的摩擦处理,且不对螺栓施加预拉力,实际上就是高强度螺栓按照普通螺栓的受力方式使用.两根H型钢通过螺栓拼接形成一根梁,在钢平台设计时将该拼接节点视作刚性节点.
有关钢梁的螺栓拼接节点的性能,国内外学者进行了一些研究.国外学者Kulak等[6]对仅进行腹板拼接的H型钢梁进行了试验研究,测量了腹板螺栓孔在挤压作用下的变形方向,确定了设计中的剪力偏心矩.Sheikh-Ibrahim等[7]研究了翼缘采用焊接拼接板或者无拼接、腹板采用高强度螺栓拼接板(螺栓无预拉力)的钢梁剪力和弯矩分别在翼缘拼接板和腹板拼接板中的分配问题.Zygomalas等[8]对有无高强度螺栓拼接板的H型钢梁跨中挠度进行了比较试验.国内学者的研究主要针对超高层钢结构的钢梁拼接,如李启才等[9-12]将钢梁高强螺栓拼接节点作为梁柱连接节点的一部分进行试验研究,分析其承载力、耗能能力以及高强螺栓的摩擦系数、拼接板厚度对拼接节点性能的影响,但并没有对单纯钢梁的拼接节点进行研究.
因此,本文结合爬升整体钢平台模架装备的工程应用,对H型钢梁高强度螺栓拼接板节点进行试验研究,分析其抗弯承载力和刚度性能.
1 试验概况
1.1 试件设计
本试验共设计了2个具有高强度螺栓拼接板节点的H型钢梁试件,均采用HN400×200×8×13型钢、8 mm厚拼接板和8.8级M22高强度螺栓(板上螺栓孔直径23 mm),型钢和拼接板均为Q345B钢材.2个试件的区别在于腹板拼接螺栓数目不同,节点参数详见表1.钢梁试件以及拼接节点的几何尺寸详见图1.

表1 螺栓拼接节点参数
本试验的钢梁拼接按照等强度和等抗弯刚度相等设计,其中,等抗弯刚度是指拼接截面的惯性矩Ip不小于被拼接H型钢梁本身的截面惯性矩I.
1.2 钢材力学性能试验
本文针对H型钢的翼缘和腹板以及拼接板,进行了3种情况的Q345B钢材力学性能试验.试样均为板材,按照有关标准进行加工和拉伸试验[13-14],试验结果的平均值如表2所示.
1.3 加载及测试方案
如图2~4所示,两个钢梁试件均采用两端简支、四点对称单调加载.为防止试验过程中钢梁整体侧向弯扭失稳,采用了侧向支撑.
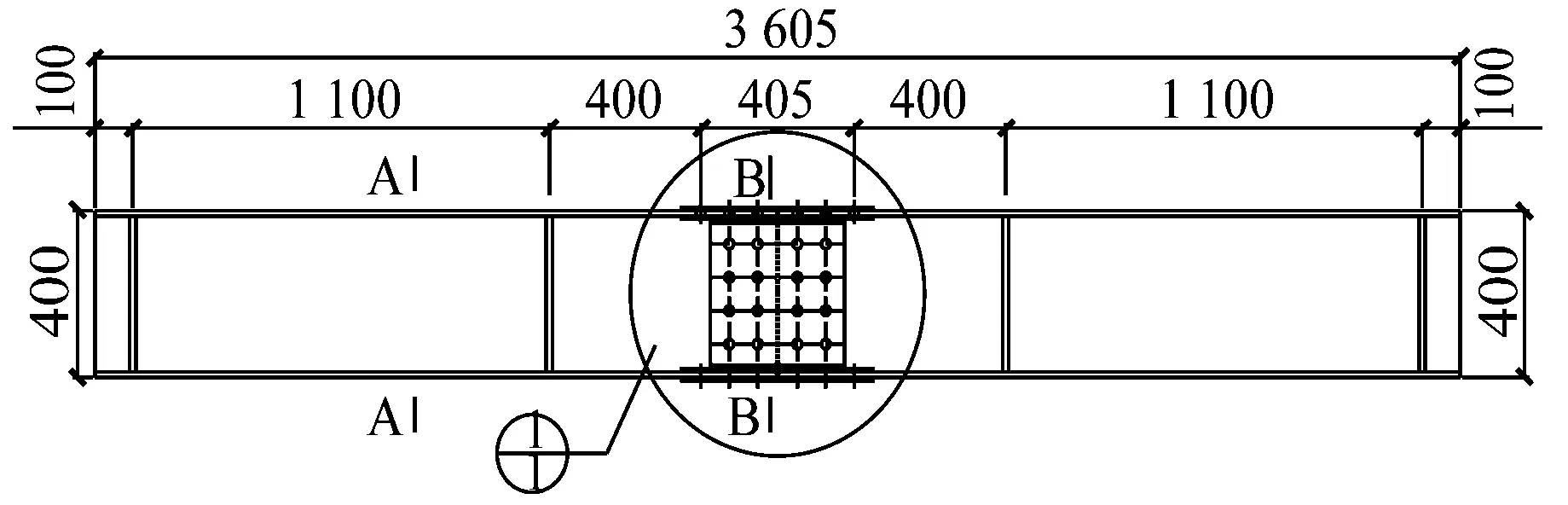
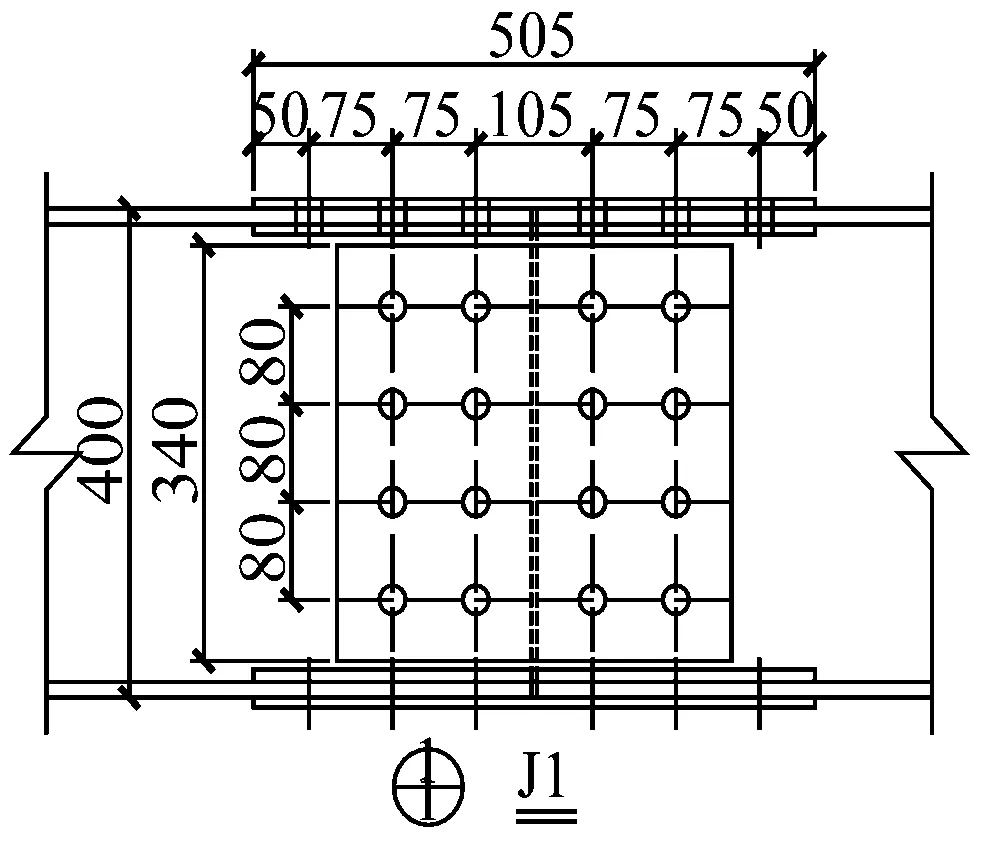
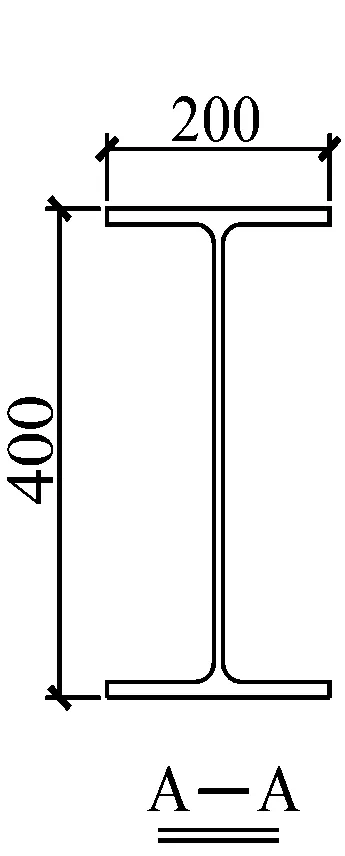
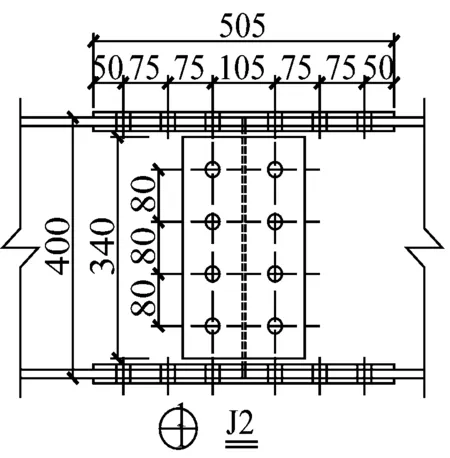
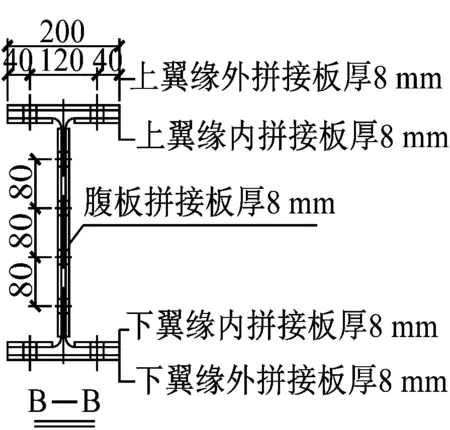
图1 试件及螺栓拼接节点尺寸(单位:mm)
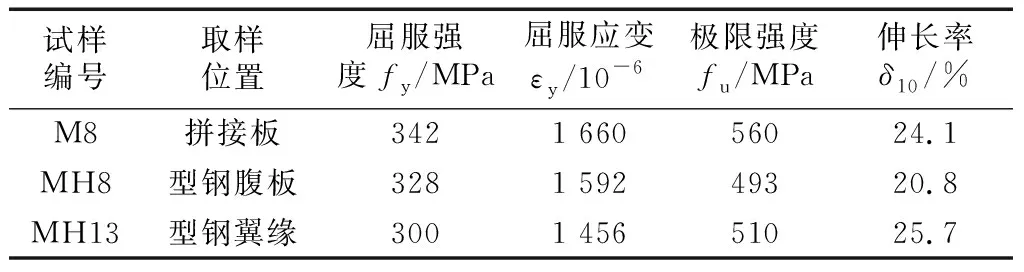
试样编号取样位置屈服强度fy/MPa屈服应变εy/10-6极限强度fu/MPa伸长率δ10/%M8拼接板3421 66056024.1MH8型钢腹板3281 59249320.8MH13型钢翼缘3001 45651025.7
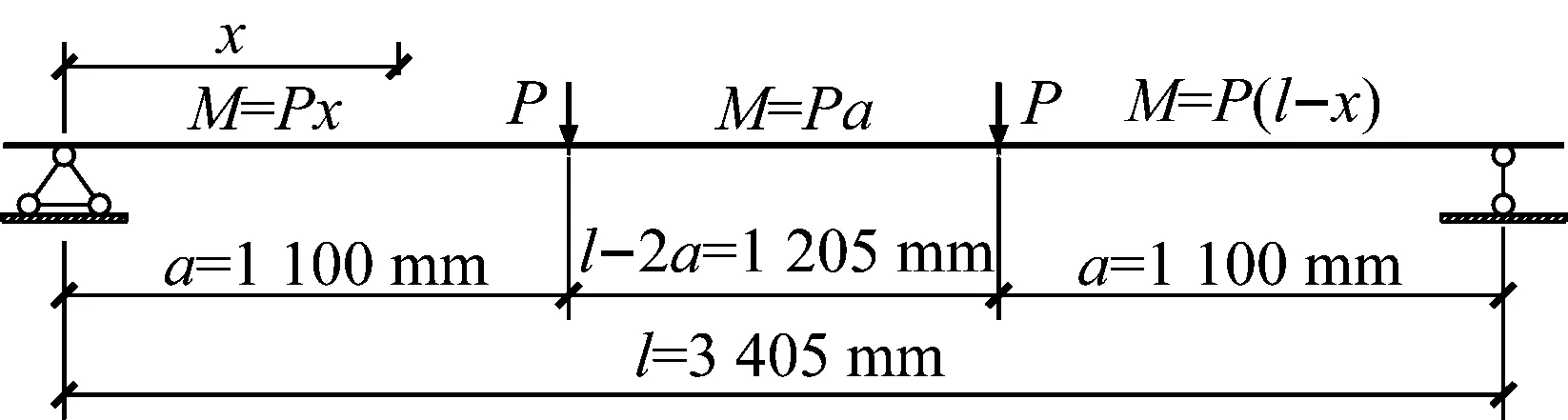
图2 试件加载图式
按照《钢结构设计规范》(GB20017—2003)[15],预估节点承载力P=265 kN.试验先预加载60 kN,大约为预估荷载的20%,观察应变片及位移计读数无异常后进行正式加载.
试验中采用位移计、应变片来测量钢梁及其拼接部位的位移、应变.两个试件的位移计及应变片的布置完全相同,具体布置如图5所示,其中1—1和3—3为H型钢梁截面,2—2为拼接板截面.
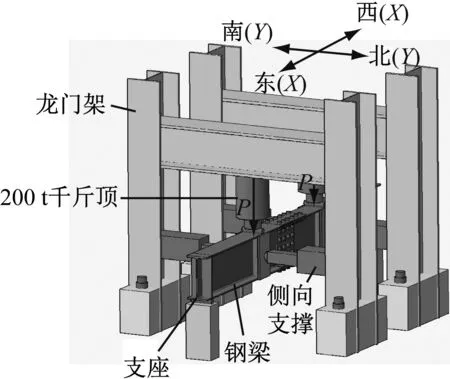
图3 试验加载装置

图4 试验现场
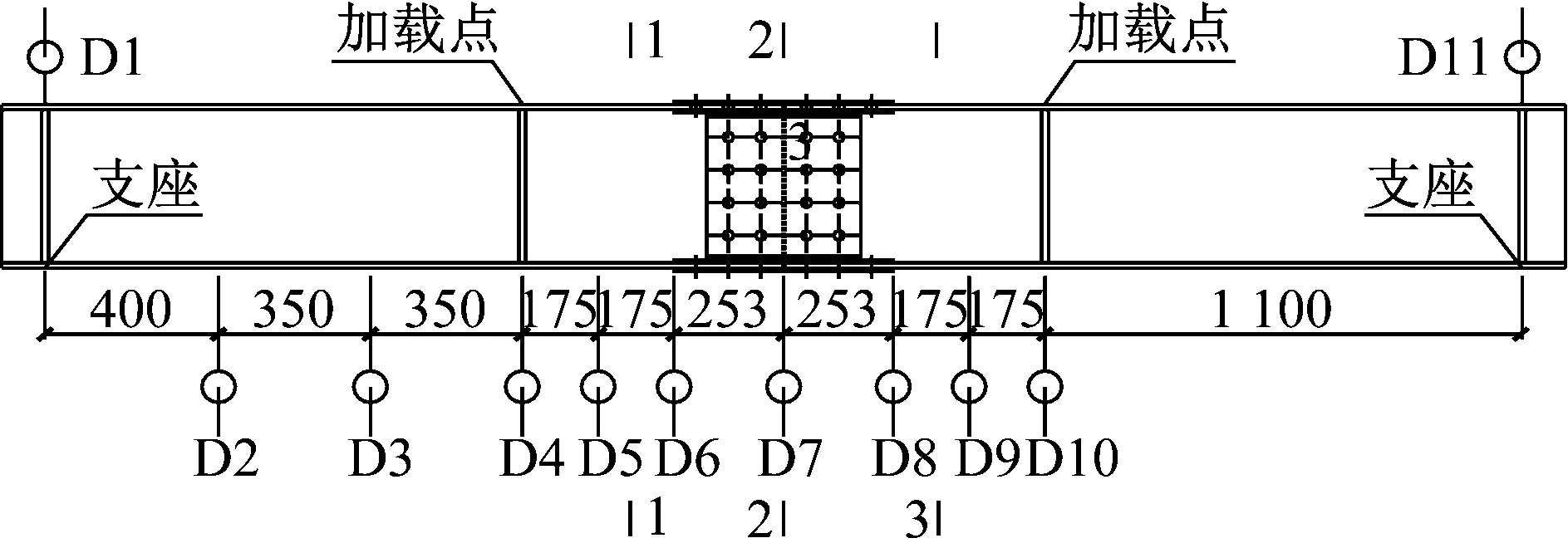
a 位移计布置

b 应变片布置
2 试验结果和分析
2.1 拼接钢梁破坏模式分析
两个拼接钢梁试件在荷载作用下的最终破坏模式相同,均为纯弯段非拼接处钢梁上翼缘受压屈曲,随后试件丧失承载力,破坏形态如图6所示.

a 试件J1b 试件J2
图6试件受弯破坏模式
Fig.6Bendingfailureofspecimens
2.2 拼接钢梁荷载-挠度曲线
图7给出了试件J1和J2跨中截面2—2在加载过程中的荷载-跨中挠度曲线,可见两个试件的曲线走势基本一致.该曲线基本上可分为6个阶段:①摩擦传力的线弹性阶段(虽然没有对螺栓施加预拉力,但仍有一定的摩擦力);②螺栓滑移阶段,此时螺栓所受剪力大于板间摩擦力而突然产生滑移;③螺栓抗剪、承压传力的线弹性阶段;④拼接节点屈服阶段,此时下翼缘外拼接板屈服,拼接节点进入屈服,而钢梁仍处于弹性阶段,荷载-跨中挠度曲线开始表现出非线性特征;⑤钢梁弹塑性阶段,此时钢梁的上、下翼缘均屈服,挠度的增长速度明显大于荷载的增长速度,拼接钢梁的刚度明显降低,荷载-跨中挠度曲线出现明显的弯折且非线性显著;⑥钢梁屈曲及破坏阶段,此时钢梁上翼缘受压屈曲,荷载增加不大,但钢梁挠度迅速地增加,最终丧失承载力.
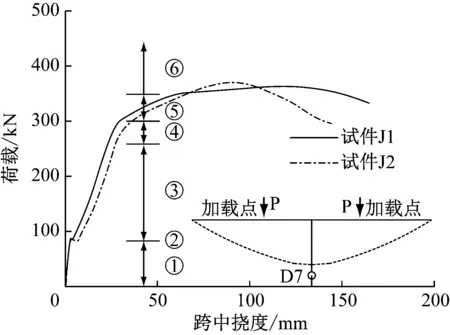
图7 试件荷载-跨中挠度曲线
2.3 拼接钢梁应变分布及荷载-应变曲线
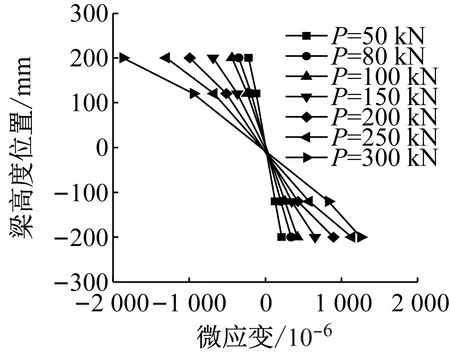
图8为试件J1和J2在1—1截面(H型钢)上的应变分布情况,由图8可见,对于处于纯弯段的1—1截面,实测应变分布符合平截面假定,且中和轴位于截面的形心处.
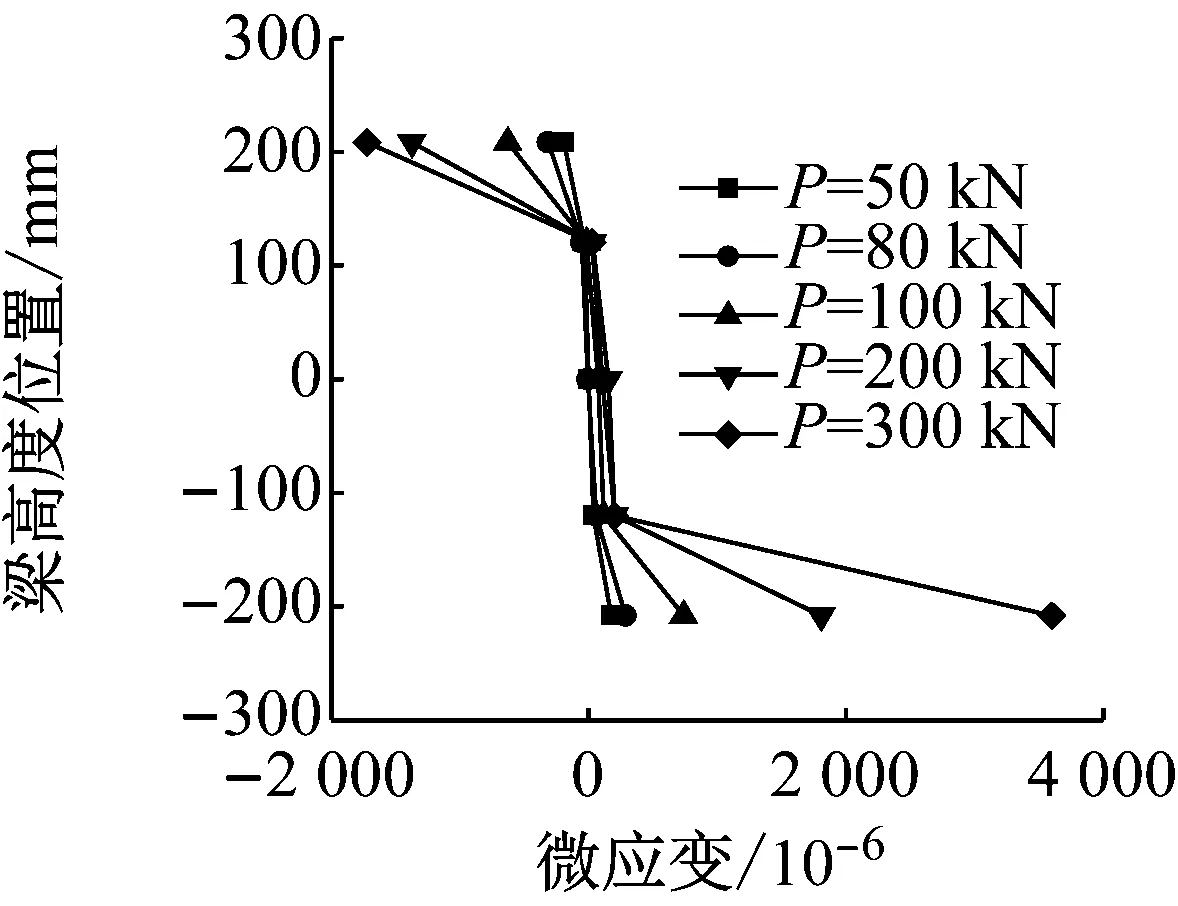
图9为2—2截面(拼接板)的应变分布情况,可知:当P<80 kN时,即螺栓滑移前,截面上的应变分布基本符合平截面假定,且中和轴位于截面形心处;当P=80 kN时,螺栓产生滑移,接触关系发生变化,中和轴上移至梁高h=120 mm处;当P>80 kN时,截面上的应变分布不再符合平截面假定,并且随着荷载的增加,腹板应变增加很小,主要靠上、下翼缘拼接板传力.
图10为试件J1和J2在3—3截面(H型钢)上的应变分布情况,可见3—3截面的应变分布情况和1—1截面基本相同,应变分布符合平截面假定,且中和轴位于截面的形心处.
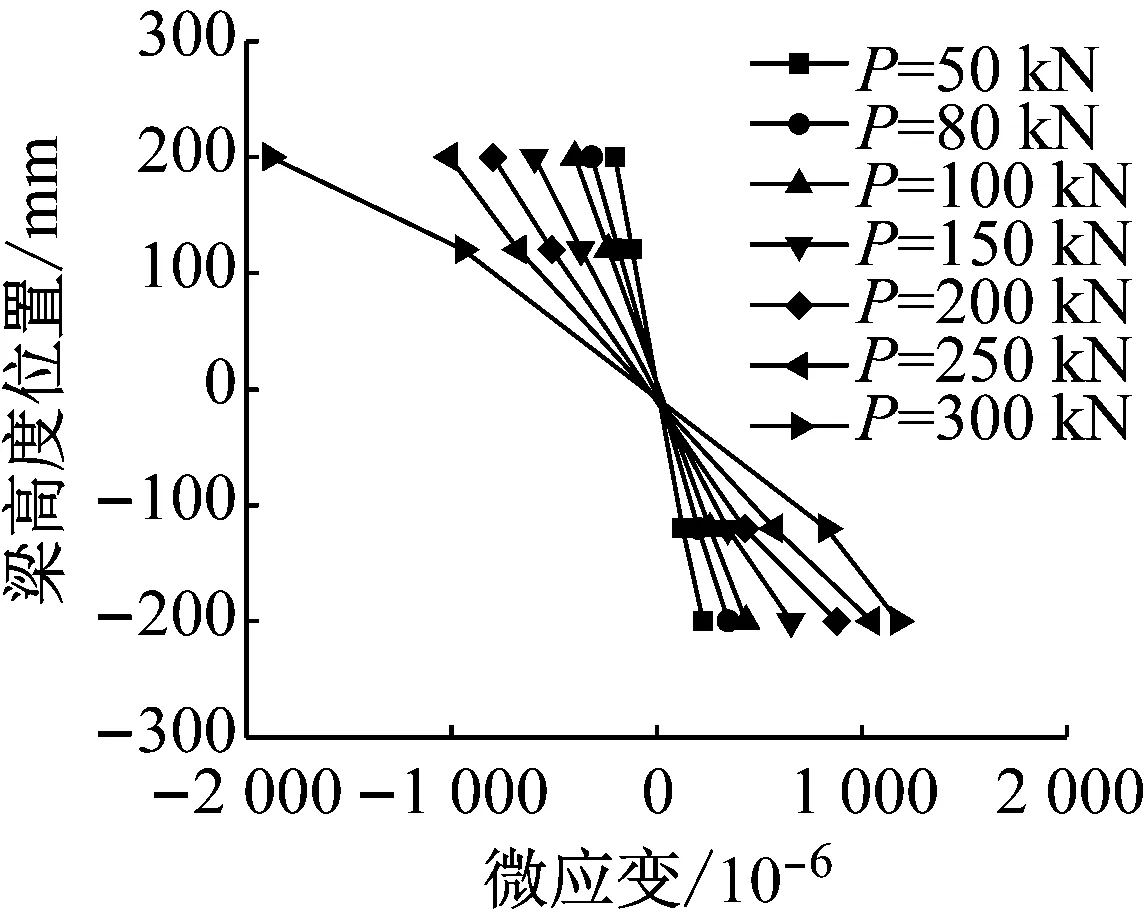
a 试件J1
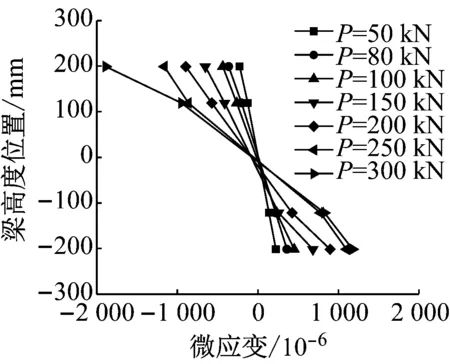
b 试件J2

a 试件J1
b 试件J2
a 试件J1

b 试件J2
2.4 拼接钢梁承载力分析
根据实测的H型钢截面尺寸及材性数据,H型钢梁的边缘屈服弯矩MB,e及全截面塑性弯矩MB,p计算值如表3所示.
根据试验现象(图7),当荷载P=80 kN时,试件J1和J2节点区螺栓出现滑移,此时作用弯矩为88 kN·m,将此弯矩定义为节点的滑移弯矩Ms.
在荷载作用下,钢梁拼接区的下翼缘外拼接板首先屈服,此时对应的弯矩定义为节点屈服弯矩My.试件J1和J2的节点屈服弯矩分别为:My1=275 kN·m,My2=237 kN·m,My2/My1=0.862.试件J2的节点屈服弯矩比试件J1低,其原因为J1和J2的腹板一侧分别采用两列和一列螺栓,在相同的荷载作用下,后者腹板拼接板分配弯矩比前者少,因此后者翼缘拼接板承担弯矩比前者多,会首先进入屈服.
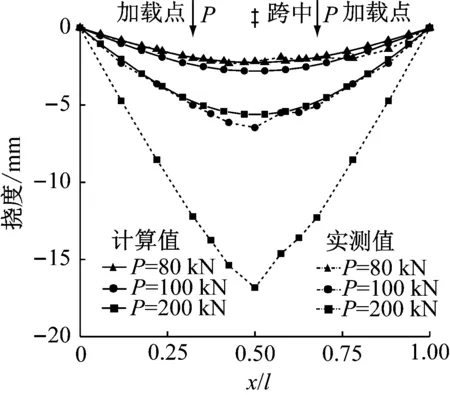
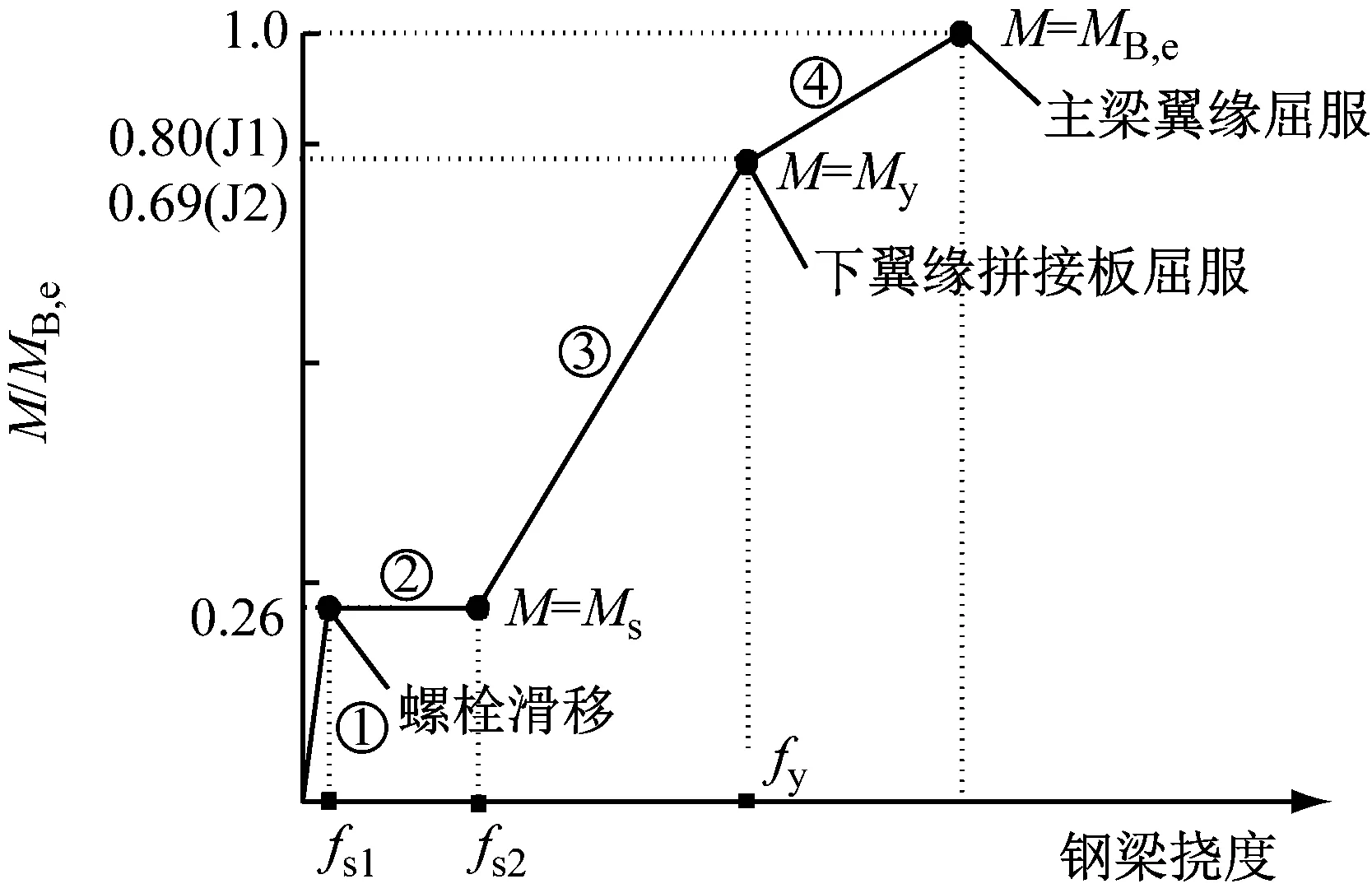
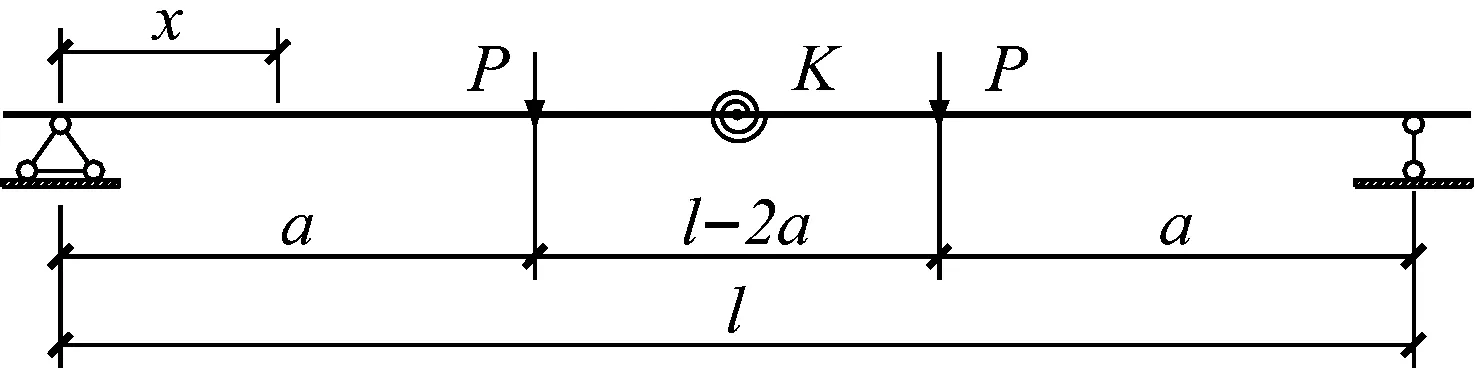
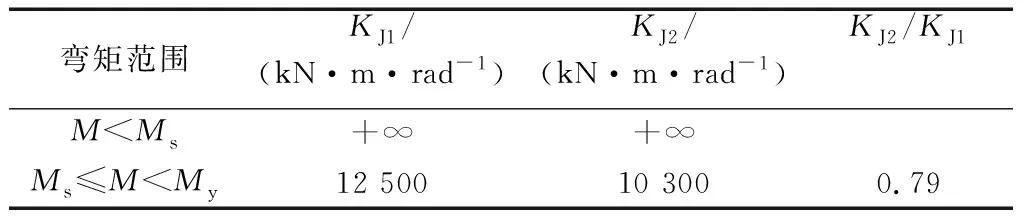
虽然本试验的钢梁拼接按照相等的抗弯刚度设计,但是由表3可知,My 表3 拼接节点抗弯承载力试验结果 试件J1和J2最终丧失承载力时均发生了钢梁非拼接段的上翼缘受压屈曲,两个试件的极限弯矩分别为Mu1=405 kN·m,Mu2=413 kN·m,如表3所示.两个试件的极限弯矩基本相等,且与钢梁全截面屈服弯矩MB,p基本相等. 在工程设计中,图1所示的H型钢梁螺栓拼接通常按照刚接处理,即拼接钢梁可视为没有拼接的钢梁.因此,图2所示荷载方式的钢梁在弹性阶段的理论挠度曲线可由式(1)计算. ft(x,M)= (1) 图11为试件J1和J2在加载过程中,钢梁的理论计算挠度曲线与实测数据的对比.当荷载P<80 kN时,即螺栓滑移之前,钢梁的实测挠度与理论计算挠度基本相同,表明螺栓拼接节点可视为刚接,钢梁可按照公式(1)计算挠度.当荷载P>80 kN、拼接螺栓滑移之后,钢梁实测挠度逐渐大于理论计算挠度,计算误差越来越大.例如,当荷载P=100 kN和200 kN时,试件J1跨中挠度的实测值与理论计算值之比分别为2.30和2.99,试件J2的情况分别为2.97和3.67,表明拼接节点达不到刚接,用于没有拼接节点的梁的理论计算挠度公式(1)已不适用,需要提出新的方法来计算螺栓拼接钢梁的挠度. 根据试件J1和J2各个位移计测得的数据分析,当M≤MB,e时,各测点的荷载-挠度曲线的基本形式如图12所示. 图12中,fs1和fs2分别为钢梁拼接节点螺栓滑移开始和结束时各测点的挠度,fy为下翼缘外拼接板屈服时,也就是节点屈服时各测点的挠度.由图12可见,当外加弯矩M≤MB,e时,荷载-挠度曲线基本分为4段:①M a 试件J1 b 试件J2 图12 M≤MB,e时螺栓拼接钢梁的荷载-挠度曲线 为了提出螺栓拼接钢梁在弹性阶段的挠度计算公式,本文引入转动弹簧来模拟具有螺栓拼接节点的钢梁抗弯刚度,如图13所示,图中K为弹簧的转动刚度.在荷载作用下,钢梁的挠度由两部分构成:①仅由拼接节点转动引起的钢梁挠度;②拼接节点无转动时钢梁产生的挠度. 图13 螺栓拼接试件的抗弯刚度理论计算模型 如图14所示,在节点弯矩M作用下,仅由节点转动引起的钢梁挠度可由式(2)计算. 图14 仅由螺栓拼接节点转动引起的试件挠度 (2) 拼接节点无转动时的钢梁挠度仍由式(1)计算.因此,计入拼接节点转动的钢梁挠度计算为 fK(x,M)=ft(x,M)+fz(x,M) (3) 进一步考虑节点滑移以及节点抗弯刚度的变化,则拼接钢梁在弹性阶段(拼接节点屈服之前)的最终挠度可按照公式(4)进行修正计算. f(x,M)= (4) 在试验过程中,已测得试件J1和J2在不同荷载作用下的挠度,因此根据公式(4)可反推得到试件J1和J2钢梁拼接节点在不同荷载阶段的转动刚度KJ1、KJ2,如表4所示. 表4 螺栓拼接节点的转动刚度K 由表4可知:当M 将表4的节点转动刚度代入公式(2),最终由公式(4)来计算拼接钢梁在节点屈服之前的弹性阶段的实际挠度.图15为公式(4)的计算挠度曲线与实测数据的对比,可见两者吻合良好,验证了公式(4)的可靠性. a 试件J1 b 试件J2 (1) 拼接钢梁在整个加载过程中的力学行为依次呈现出以下特性:钢梁和节点的弹性阶段,节点螺栓滑移的非承载阶段,钢梁和节点恢复承载力的弹性阶段,节点处受拉翼缘拼接板屈服阶段,钢梁弹塑性阶段,钢梁受压翼缘屈曲破坏阶段. (2) 拼接节点进入屈服时的弯矩试验值明显小于钢梁边缘屈服的弯矩理论计算值,前者为后者的69% ~ 80%,但是,拼接节点最终破坏时的极限弯矩试验值可达到钢梁全截面屈服弯矩的理论计算值.拼接节点破坏时的极限弯矩试验值为其进入屈服时的弯矩试验值的1.47~1.74倍. (3) 拼接节点在螺栓滑移之前,翼缘和腹板拼接板上的应变符合平截面假定,但是滑移之后不再符合平截面假定,弯矩主要由翼缘拼接板承受和传力,腹板传力很少. (4) 拼接节点的螺栓滑移对钢梁抗弯刚度有较大的影响,当螺栓未滑移时,拼接钢梁整体性好,如同未有螺栓拼接的整根钢梁,拼接节点可视为刚接,但是,当螺栓发生滑移后,钢梁抗弯刚度减小,拼接节点不能按刚接处理,相当于半刚性节点. (5) 拼接腹板上螺栓数量由双列螺栓减少至单列螺栓,拼接节点的抗弯刚度约有20%的降低. (6) 本文在试验数据分析的基础上,提出了考虑拼接节点转动刚度影响的钢梁挠度理论计算方法和公式,理论计算值与试验值吻合良好. (7) 在施工现场进行钢平台梁拼接时,建议尽可能对高强度螺栓施加预拉力,充分利用和发挥摩擦力的作用,延迟螺栓滑移的不利影响,从而提高拼接钢梁的抗弯刚度.
2.5 拼接钢梁刚度分析
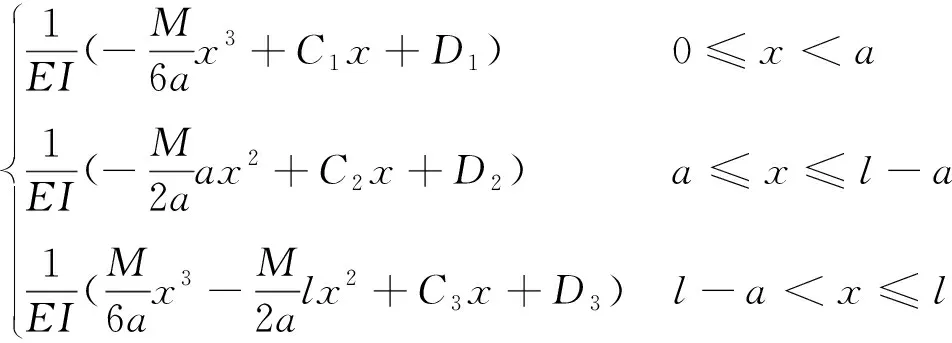




3 结论

