货币政策、人民币汇率与国际原油市场关系的实证分析
李建峰,卢新生,蒋 伟
(1.中国计量大学 经济与管理学院,杭州 310018;2.济南大学 商学院,济南 250022;3.同济大学 经济与管理学院,上海 200092)
0 引言
中国于2013年已经超过美国成为世界上最大的原油进口国,且对外依存度已超过60%,大规模的原油进口以及超高的对外依存度,势必导致中国面临巨大的原油风险。而且中国不断地放开金融市场,又会导致国际原油市场风险更加容易通过金融市场传递到国内市场。同时,中国作为世界第二大经济体,其在国际经济中的地位日益重要,中国国内形势变化也可能会对国际市场产生一定的影响。在此背景下充分把握人民币汇率和中国货币政策与国际原油市场之间的互动关系,不仅能够从容应对国际原油对于中国市场的冲击,而且能够衡量人民币汇率和中国货币政策对于国际原油市场的溢出效应,有利于政策制定者推出充分考虑内外效应的最优的货币政策。
近年来国内外学者对汇率和原油之间的关系,运用不同方法进行了大量研究。但是这些研究大都集中于发达国家,对发展中国家尤其是中国的汇率市场研究相对较少。所用方法主要是协整检验、格兰杰因果关系检验以及SVAR等方法,且研究的重点主要是一阶关系上面,而对波动溢出方面关注较少。另外还没有发现在研究两者之间互动关系时考虑央行货币政策的影响方面的文献。因此,本文主要采用VAR-BEKK-MGARCH来分析国际原油市场与人民币汇率市场之间的溢出效应,同时考虑央行货币政策操作以及国内外利差等因素的影响。
1 VAR-BEKK-MGARCH模型的设定
本文的主要任务是衡量人民币汇率市场与国际原油市场之间的溢出效应,并且考察央行货币政策操作以及国内外利差的作用,因此本文选择的最合适的模型是Engle和Kroner(1995)提出的BEKK-MGARCH模型。
为了分析人民币汇率市场和国际原油市场之间的均值溢出效应,本文假定条件均值方程服从向量自回归模型(VAR)。两变量的VAR(n)模型的设定形式为:

在BEKK-GARCH模型中残差序列的条件协方差矩阵定义为:


其中,C是一个(2×2)的下三角常数矩阵;A是一个(2×2)的ARCH系数矩阵,表示滞后一期的残差对当前市场波动率的影响,即滞后一期的新息对当前市场波动率的影响(包括对自身和市场交互影响);B是(2×2)的GARCH系数矩阵,代表滞后一期的条件波动率对当前波动率的影响(包括对自身和市场交互影响)。
其中,εt是一个从条件均值方程中得到的(2×1)残差向量。Ωt-1是t-1时刻的信息集。根据BEKK-MGARCH模型的表达式为:
2 数据描述和初步分析
本文选取五个人民币汇率的日数据,包括人民币兑欧元(EUR/CNY)、人民币兑英镑(GBP/CNY)、人民币兑日元(JPY/CNY)、人民币兑美元(USD/CNY)和人民币兑澳元(AUD/CNY),所有汇率数据来源于FRED数据库。国际原油价格选取布伦特(Brent)原
油现货价格的日数据,数据来源于美国能源信息局(EIA)。人民币利率选取7天上海银行间同业拆借利率SHIBOR,数据来源于SHIBOR官网。其他外币利率则选取7天伦敦同业拆借利率LIBOR,数据来源于FRED数据库。中国央行货币政策操作数据来源于中国人民银行网站。样本期为2006年10月9日到2016年9月30日。研究对象主要为汇率和原油价格的对数差分序列:

图1给出了原油市场价格、人民币汇率以及收益率的走势图。原油与人民币汇率总表现出相同或相反的趋势,这说明原油市场与人民币汇率市场联系比较紧密。

图1 人民币汇率市场与布伦特原油收益率和价格
从表1的统计描述结果可知,所有收益率序列均值都接近于零,标准差最大的是Brent原油(0.996),表明原油市场波动远大于人民币汇率市场。JB统计量和偏度数据说明所有的序列都不服从正态分布。而汇率和原油收益率序列的峰度都大于3,说明这些序列都具有“尖峰厚尾”性质。Ljung-Box Q检验结果表明所有的序列及其平方序列均存在不同程度的自相关,即所有序列具有波动集聚性。ADF和PP单位根检验结果表明所有收益率和利差序列都是平稳时间序列。异方差效应检验结果则说明所有序列都存在异方差效应,这说明本文采用多元GARCH模型是合理的。
3 实证分析
本文在估计多元波动率模型时假定残差服从t分布过程。条件均值方程的最优滞后阶数根据AIC和SIC信息准则综合确定。因此本文在对原油和人民币汇率市场波动率进行建模时选择BEKK-MGARCH(1,1)模型,并考察中外利差以及央行货币政策操作对两者互动关系的影响。
3.1 国际原油市场与人民币汇率市场溢出效应分析
表2是基本模型的估计结果。从均值方程估计结果中可以发现原油市场对人民币兑英镑、日元以及澳元有显著均值溢出效应,人民币兑英镑对原油有均值溢出效应。从方差层面来看存在从原油到人民币汇率的波动溢出效应,而在相反的方向上,仅存有人民币兑英镑会对国际原油产生波动溢出效应。
3.2 国内外利差的影响
本文将利差变量引入VAR-BEKK-MGARCH模型中,从而来衡量利差对人民币汇率和国际原油市场的影响,估计结果如下页表3所示。
从均值层面来看,中日利差、中美利差和中澳利差会对相对应的汇率产生显著影响。而中欧、中英和中澳利差则会对Brent原油的收益率产生明显的负向影响。从波动层面来看,国内外利差会对人民币汇率市场波动有明显正向作用,而中欧、中英和中澳利差的系数估计结果表明这几个利差变量会对原油市场的波动率产生显著负向影响。

表2 人民币汇率与国际原油的VAR-BEKK-MGARCH(1,1)估计结果①本文所有模型中的第一个变量为汇率,第二个变量为原油;FX和O分别代表汇率和原油;所有模型估计结果均通过相应检验,为节省篇幅本文所有多元模型仅给出交叉项或者外生变量的估计结果。
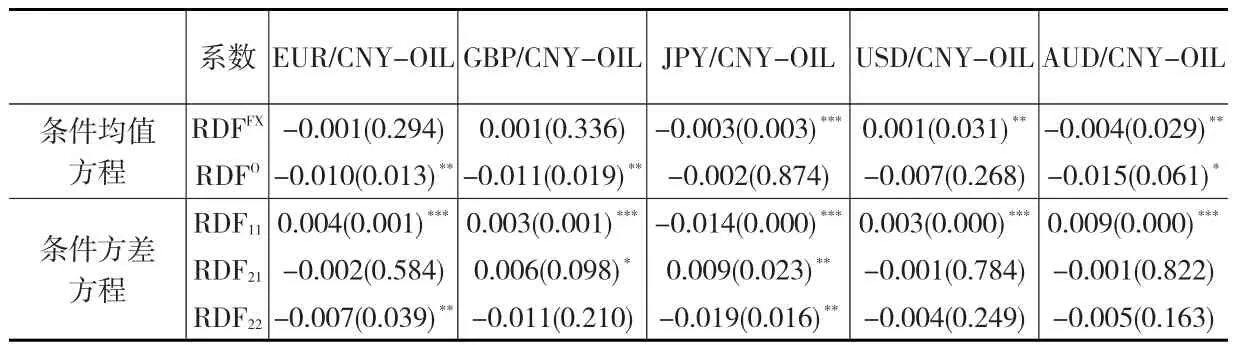
表3 引入国内外利差变量的VAR-BEKK-MGARCH估计结果
3.3 利率和准备金率调整的影响
利率和法定存款准备金率调整总体来说可以分成两类:上调利率和准备金率的操作称为紧缩性货币政策,以MPC代表;下调利率和准备金率的操作称为扩张性货币政策,以MPE代表。本文将这两类货币政策操作变量引入VAR-BEKK-MGARCH模型,从而来衡量利率政策和准备金率政策对市场以及市场间溢出关系的影响。MPC和MPE以虚拟变量的形式引入模型,虚拟变量的构造方法为:当有货币政策调整时,该日的变量值设定为1,否则为0。引入利率和准备金率变量后的估计结果如表4所示。
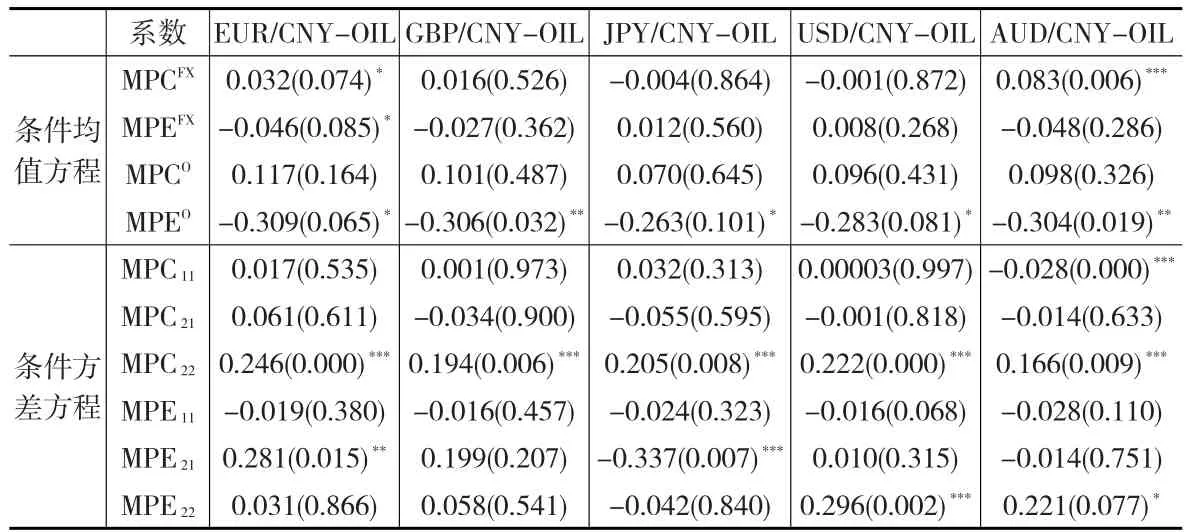
表4 引入利率和准备金率调整变量的VAR-BEKK-MGARCH估计结果
从均值方程来看,紧缩型货币政策调整(MPC)会导致人民币兑欧元和澳元汇率升值,但对国际原油市场无明显影响;扩张型货币政策调整仅会导致人民币兑欧元汇率明显贬值和国际原油收益率下降。从波动层面来看,中国货币政策调整对人民币汇率市场波动并无明显影响,而紧缩型货币政策调整则会加剧国际原油市场的波动。
3.4 互动关系分析
本文构造公开市场操作变量进而研究公开市场操作、人民币汇率与国际原油市场之间的互动关系,数据采用周数据形式。
公开市场操作变量构造方法为:
第一步:假定ΔBt,kt,(t=1,2,…,T)分别表示第t期央行公开市场操作的净货币投放量和货币乘数,则第t期央行公开市场操作导致的货币供应量增加量为ΔMt=ΔBt*kt。
第二步:计算累积货币供应量。
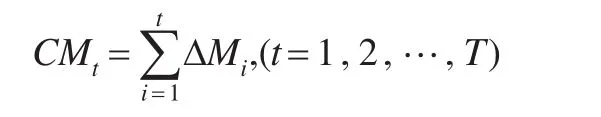
第三步:构造公开市场操作变量。
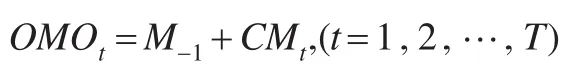

表5 引入央行公开市场操作变量的VAR-BEKK-MGARCH估计结果
其中,M-1表示样本期前一刻的货币供应量,在本文中为2006年9月的货币供应量。这样就得到一个反映央行公开市场操作的政策变量。取人民币汇率、公开市场操作变量及原油价格的对数收益率并建立三元VAR-BEKK-GARCH模型,估计结果如表5所示。
从均值方程来看,中国公开市场操作并不会对人民币汇率市场和国际原油市场收益率产生明显的冲击,人民币汇率和国际原油价格的变化也不会对公开市场操作产生显著的影响。从波动层面来看,人民币兑英镑汇率及国际原油市场波动变化均会导致公开市场操作波动发生相应的变化,而中国央行公开市场操作则不会对人民币汇率和国际原油市场波动产生明显影响。
4 结论
本文运用二元和三元VAR-BEKK-MGARCH模型对人民币汇率制度改革后的人民币汇率市场、央行货币政策和Brent原油市场之间的互动关系进行研究,结论如下:
(1)人民币兑英镑汇率与国际原油之间存在双向的均值和波动溢出效应,国际原油价格变化会导致人民币兑英镑和澳元汇率发生相应的改变;国际原油市场波动也会导致人民币汇率市场波动明显的变化。
(2)中日、中美和中澳利差会对相应的人民币汇率的收益率产生显著影响,中欧、中英和中澳利差改变会使Brent原油市场收益率有明显变化;中外利差会对人民币汇率市场波动率产生显著影响,同时中欧和中日利差会对原油市场波动发生显著改变。
(3)央行公开市场操作不会对人民币汇率和国际原油市场产生影响,国际原油市场波动会对央行公开市场操作产生显著影响。
(4)紧缩性货币政策调整对人民币兑欧元和人民币兑澳元的收益率作用明显,扩张性的政策调整会对人民币兑欧元和Brent原油市场的收益率产生显著影响;同时紧缩性货币政策调整会显著影响原油市场的波动率。

