不同渠道权利结构下闭环供应链定价与服务决策

高 洁

（1.四川大学—香港理工大学 灾后重建与管理学院，成都 610207;2.四川旅游学院 经济管理学院，成都 610100）

1 问题的提出

近些年，再制造在许多行业都非常普遍[1]，从打印机墨盒，计算机，家具、电器设备、工程机器到汽车行业[2]，已成为企业盈利和迅速扩大的业务。例如，通过使用可重用的部件和材料，施乐公司在其制造过程中节约40%～65%制造费用[3]。实践表明，废旧产品回收再制造不仅有助于提高企业对资源的利用率、塑造良好的社会形象，而且也能为企业创造利润、提高竞争力。

由于闭环供应链的定价策略直接影响到供应链系统运作效率，因此受到国内外学者的广泛关注。Savaskan RC等[4]研究了不同回收渠道对闭环供应链中定价及利润的影响；顾巧论等[5]分别得出Stackelberg博弈和Nash均衡两个非合作博弈的定价决策和一个联合定价决策，并对比分析了不同定价策略的效率；葛静燕等[6]用博弈论方法分析了零售商负责回收的二级闭环供应链在分散决策下的最优价格策略，并得出了闭环供应链存在双重边际加价效应的结论。王文宾等[7]讨论了回收努力程度与产品定价的区别，分析了制造商与零售商的利润随消费者偏好系数的变化规律。颜荣芳等[8]构建了再制造闭环供应链差别定价模型，分别讨论了集中化和分散化决策下的最优定价决策问题。高洁等[9]分集中决策和分散决策两种情况研究技术许可下闭环供应链的定价决策问题。从已有文献来看，多数文献仅考虑了产品的定价策略而未考虑服务水平策略对再制造闭环供应链的影响。然而，研究表明服务水平不仅会影响消费的购买需要和企业的定价决策，还会对供应链系统收益产生影响[10-13]。关于闭环供应链定价与服务决策相关研究的文献主要有：卢震等[10]研究了在具有服务和回收再制造的双渠道下，闭环供应链的渠道设计问题;朱海波[11]研究了考虑服务水平的闭环供应链网络规划模型；Wu[12]研究了一个制造商，一个再制造商和一个共同零售商之间的价格和服务竞争，使用两阶段优化方法和Nash博弈；Zhang等[13]主要探讨零售服务对集中式和分散式双渠道闭环供应链中的渠道成员的定价决策和渠道绩效的影响。基于以上研究，本文主要考虑了废旧产品收集过程中的反向渠道竞争，并针对制造商和零售商之间不同类型的权利结构，即制造商Stackelberg博弈，零售商Stackelberg博弈和Nash博弈来对比讨论3种不同权利结构下的定价和服务水平策略问题。

本文分析了一个制造商和一个零售商组成的闭环供应链，制造商可以通过新的组件和原材料生产新的产品，也可以通过再制造废旧产品为新产品。为了增加废旧产品回收率，本文假设，制造商和零售商竞都可以从客户手中回收废旧产品且存在竞争关系，使用博弈论模型，主要研究以下问题。（1）从整体闭环供应链的角度，三种类型的渠道权力结构（制造商Stackelberg，零售商Stackelberg和Nash博弈），哪一种是最好？（2）最佳零售商增值服务水平、价格和废旧产品回收率在三种不同的博弈模型下如何变化？（3）研究了零售商增值服务水平和渠道回收竞争强度对供应链成员最优决策的影响。（4）然后，比较了不同权利结构下制造商、零售商和整个供应链的利润。

2 相关参数符号说明及模型的前提假设

2.1 相关参数符号说明

考虑一个由单个制造商和单个零售商组成的单周期二级供应链。其中，制造商只通过零售商销售其新产品和再制造产品。制造商与零售商均进行回收活动，两条回收渠道之间存在竞争，制造商利用回收的旧产品进行再制造。制造商、零售商之间的相互关系及相关决策变量如图1所示。

图1 闭环供应链结构模型

本文构建模型主要用到的参数符号有：a表示潜在市场规模；α表示两回收渠道之间的竞争强度，取值范围为：0≤α＜1；β表示消费者对零售价格的敏感系数；θ表示零售商增值服务对需求的敏感系数；p表示单位产品零售价格；s表示零售商提供的增值服务水平；D表示对产品的市场需求；w表示单位产品批发价格；cm表示新产品的单位生产成本；cr表示再制造产品的单位生产成本；τm表示制造商的回收率；τr表示零售商的回收率；b表示零售商将回收的废旧产品卖给制造商得到的单位补贴，且0＜b≤cm-cr；C表示规模参数。

2.2 模型的前提假设

本文的研究将基于以下假设：

假设1：假设再生产品的单位生产成本cr低于新产品的单位生产成本cm，即cr＜cm[11]。

因此，制造商的平均单位成本可以表示为-c=(1-τ)cm+τcr，其中τ=τm+τr。令 Δ=cm-cr,则平均单位成本可以表示为-c=cm-τΔ。

假设2：假设当回收废旧产品时两个逆向渠道之间存在竞争，根据文献[14],制造商和零售商的废旧产品回收率满足以下关系：

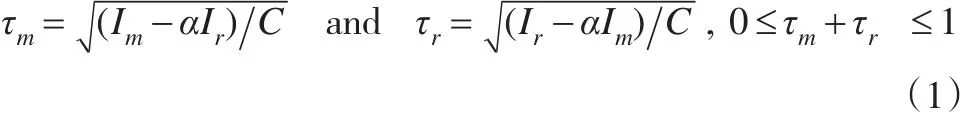
其中0≤α＜1,Im和Ir分别代表制造商和零售商为回收废旧产品所做出的投资成本。

假设3：假设零售商可以提供增值服务来刺激市场需求，零售商提供增值服务的成本函数可以表述为[17,18]：

假设4：假设制造商生产的新产品和再制造产品质量一致，且以相同的价格批发给零售商，同时消费者对新产品和再制造产品的接受程度相同[14]。

假设5：假设与价格相关的市场需求函数是线性的[15]，设为：

假设6：假设制造商和零售商的信息完全对称，且制造商拥有的产能足以满足产品的市场需求。

3 三种渠道权利结构下的闭环供应链决策模型

本文拟分制造商与零售商Nash博弈(无领导者的市场博弈)、制造商-Stackelberg博弈、零售商-Stackelberg博弈三种渠道权力结构对双渠道回收且零售商提供增值服务情况下再制造闭环供应链的有关问题进行研究。在这三个分散决策模型中，零售商和制造商都是风险中性和理性的，即整个决策过程中双方都是以最大化自己的利润为目的。

根据上述说明和假设，可得制造商和零售商的利润函数分别为：

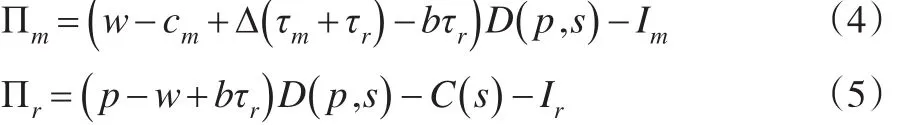
将Im和Ir代入公式（1）和公式（2），可以得到：

3.1 模型N：制造商和零售商Nash博弈

制造商和零售商Nash博弈即无领导者的市场博弈，假设制造商和零售商同时做出决策，制造商决定批发价格w和回收率τm，零售商决定零售价p，增值服务水平s和回收率τr。为了使πm和 πr最大化，先研究一些相关命题。

命题1：（1）利润函数πm是关于w和τm的联合凹函数；（2）利润函数 Πr是关于p和τr的联合凹函数，然而，无法判断Πr是关于p和s的联合凹函数。

证明：求出 πm关于w和τm的二阶导数，得到海塞矩阵:

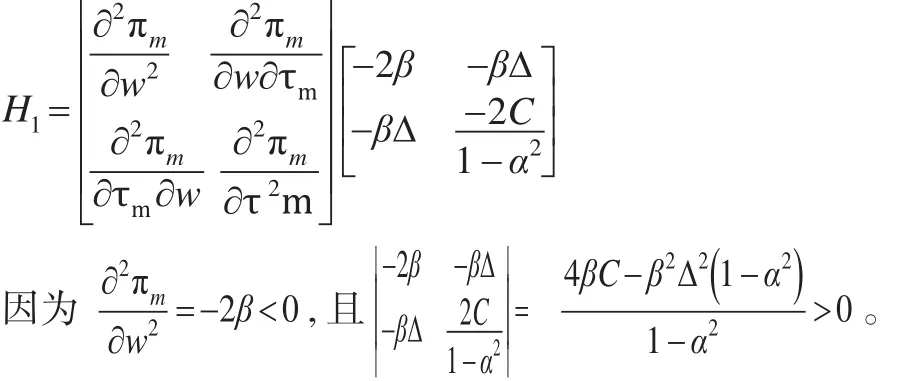
所以,πm是关于w和τm的联合凹函数。

同理可证 πr是关于p和τr的联合凹函数，但 πr不是关于p，s和τr的联合凹函数。

结论（1）表明可以通过对函数Πr一阶求导得到w和τm的最优值；结论（2）表明不能通过对函数Πr一阶求导直接得到出 p,τr和 s的最优值，然而对于任何给定的s，Πr有关于 p和 τr的唯一最优解，因此可以使用两阶段优化方法来解决这个问题，即首先对一个给定的s得到Πr的最优解，然后推导出使πr最大化的s的最优解。

根据命题1，有以下结论：

命题2：对于给定的 s，制造商和零售商的最优解如下：

从命题2，可以发现：

即，对于任何给定的s，随着α的增加，制造商和零售商废旧产品的回收率减少，而制造商的批发价格和零售商的零售价格随着α的增加而增加，这一结果和文献[14]是一致的。

为了验证服务水平s对零售价格 p,批发价格w,制造商废旧产品回收率τm和零售商废旧产品回收率τr的影响，基于 pN*(s),wN*(s),(s)和(s)，得到以下结论：

命题3：在N模型中，服务水平s对零售价格 p,批发价格w,制造商废旧产品回收率τm和零售商废旧产品回收率τr的影响如下：

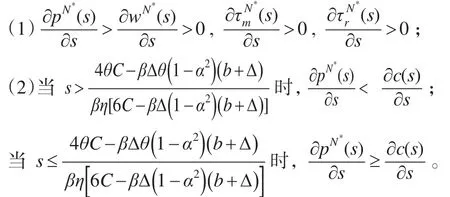
命题3中（1）表明，对于给定的α，最优批发价格，零售价格，制造商回收率和零售商回收率随着s的增加而增加。这与人们的直觉相一致，即如果服务水平高，市场需求将会增加，制造商和零售商的回收率也将会增加，批发价格和零售价格也会更高；从（1）中还能得到，对于给定的α，pN*(s)关于服务水平s的变化率比wN*(s)关于服务水平s变化率的要大。

命题3：中（2）表明，当服务水平s超过阈值时，服务水平s增加一个单位所发生的成本高于零售价格的增加，这意味着提供更高的服务水平时零售商的边际利润下降。然而，当服务水平低于阈值，如果服务水平增加一个单位，零售价格将增加超过产生的服务费用，这意味着零售商可以通过提高服务水平来获利。

将公式（8）代入公式（7）,可以得到：

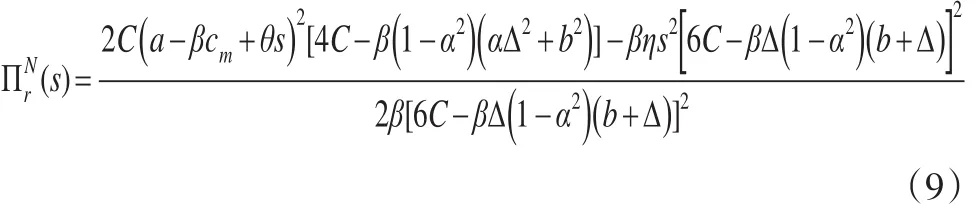
将公式（10）代入公式（6）至公式（8）,可以推导出最优的批发价格，最优的零售价格，最优的废旧产品回收率。

3.2 模型M:制造商Stackelberg博弈

在制造商领导的Stackelberg博弈中，制造商是领导者而零售商是追随者。这种竞争模式在实践中很普遍。在这种情形下，制造商首先给出新产品的单位批发价格w和废旧产品的回收率τm，然后，零售商根据制造商的决策，给出新产品的单位零售价格 p，废旧产品回收率τr和服务水平s。

从公式（6）和公式（7），得到以下结论：

命题4：对于给定的 s,制造商和零售商的最优决策如下:

类似于N模型，通过分析得出：对于给定的s，批发价格wM*和零售价格 pM*随着α的增加而上涨，而制造商的废旧产品回收率和零售商的废旧产品回报率随着α的增加而降低。

为了验证服务水平s对零售价格 p,批发价格w,制造商废旧产品回收率τm和零售商废旧产品回收率τr的影响，基于 pM*(s),wM*(s),(s)和(s)，得到以下结论：

命题5：在M模型中，服务水平s对零售价格 p,批发价格w,制造商废旧产品回收率τm和零售商废旧产品回收率τr的影响如下：

命题5中（1）表明,对于给定的α,最优批发价格wM*,零售价格pM*,制造商的废旧产品回收率和零售商的废旧产品回收率随着服务水平s的增加而增大。但零售商的边际利润并不总是会随着s的增加而增大。

命题5中（2）表明，对于给定的α，当服务水平s低于阈值时,零售商能够通过改进服务水平获利，但是当服务水平s超过阈值时，提供更高的服务水平则零售商的边际利润下降。

将公式（11）代入公式（7）中，可以得到：

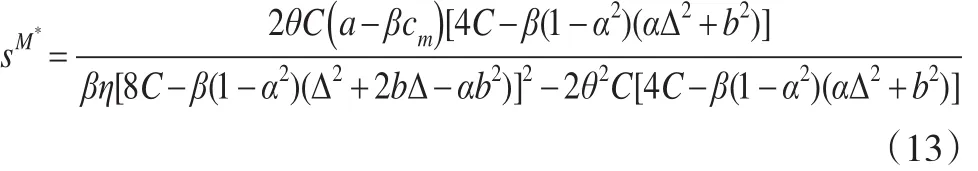
将公式（13）代入公式（6）和公式（7）和公式（11），可以得到最优批发价格，零售价格，废旧产品回收率和渠道利润。

3.3 模型R：零售商-Stackelberg博弈

随着零售商的力量的显著增加，例如国际零售巨头沃尔玛、家乐福等，比其他供应链成员在各自的供应链中更占主导地位。在零售商领导的Stackelberg博弈中，零售商首先决策零售价格 p，废旧产品回收率τr和服务水平s，然后，制造商根据零售商的决策，给出新产品的批发价格w和废旧产品回收率τm。由于问题的复杂性，本文采用两阶段优化法进行分析。第一阶段，对于给定的服务水平s推导出最优零售价格和废旧产品回收率；第二阶段，基于上阶段得到的最优解得到最优服务水平s。得到如下命题：

命题6：对于给定的s,制造商和零售商的最优决策如下：

命题7：在R模型中，服务水平s对零售价格 p,批发价格w,制造商废旧产品回收率τm和零售商废旧产品回收率τr的影响如下：

与上述模型相似，在R模型中，可以得出对于给定的α,最优批发价格wM*,零售价格 pM*,制造商的废旧产品回收率和零售商的废旧产品回收率都随着服务水平s的增加而增加。对于服务水平s也同样存在阈值，当服务水平s低于阈值，零售商可以通过提高服务水平获利，但是当服务水平s超过阈值时，提供更高的服务水平则零售商的边际利润下降。

将公式（14）代入公式（7）得到：

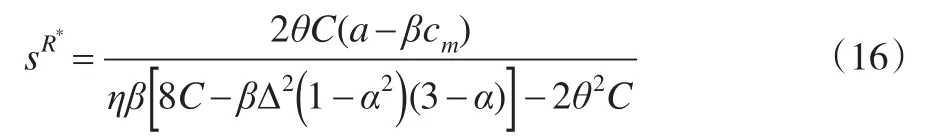
将公式（16）代入公式（6）至公式（7）和公式（14），可以推导出最优批发价格,最优零售价格,最优产品回收率和渠道利润。

4 三种博弈模型之间的比较

上文总结了三种博弈模型的最优解，通过比较可得出以下结论：

命题8：三种权利结构模型下的最优废旧产品回收率满足 τM*＜τR*＜τN*。

命题8表明竞争强度不影响三种模型下的废旧产品回收率的大小关系，比较发现N模型下制造商回收废旧产品是最优的，而M模型是最不好的选择。因此，从环境保护的角度来看，没有领导者的市场对整个行业有益。然而，当整个行业只考虑两种Stackelberg模型时，R模型优于M模型。

命题9：三种权利结构博弈模型下最优批发价格和最优零售价格满足以下关系：wM*＞wN*＞wR*和 pR*＞pM*＞pN*。

命题9表明，无论竞争强度如何，批发价格最高的是M模型，最低的是R模型。

这是因为在制造商Stackelberg博弈模型下，制造商有很强的批发价格最大化的动机。类似的，在零售商Stackelberg模型下，零售商有足够的权力来迫使制造商设置更低的批发价格[16]。然后通过比较，进一步发现在三种权利结构模型中R模型的零售价格价格是最高的，而N模型中零售价格是最低的。这与一般所认为的更低的批发价格将会导致降低零售价格相违背，原因是在零售商Stackelberg博弈模型下，零售商不仅可以迫使制造商设置较低的批发价格，也可以强迫消费者接受更高的零售价格。

命题10：三种权利结构模型下的最优服务水平排序关系如下：sM*＜sN*＜sR*。

从命题10：可以观察到R模型下服务水平是最高的，而M模型下最低。

这是因为，在R模型中，由于更高的零售价格所带来的利润增加，抵消了由于更高的服务水平而导致的每单位收入的损失。因此，在零售商Stackelberg模型下，零售商将设置更高的服务水平。然而，在M模型中，由于较高的服务水平导致的利润增加无法抵消由于较高的批发价格而导致的每单位收入的损失。因此，在制造Stackelberg模型下，零售商将设置更低的服务水平。

命题11：制造商的利润，零售商的利润和整个供应链利润关系如下和

从命题11，可以发现在M模型中制造商的利润最大，而在R模型中制造商的利润最小，然而，零售商的利润则正好相反。因此，有直接激励制造商和零售商成为领袖。然而整个供应链的的利润在N模型，即没有市场领袖时是最大的。然而，无市场领导者的市场结构不是一种稳定的市场结构，因为Stackelberg领导者总是能获得更多利润，制造商和零售商都有成为市场领导者的愿望。

5 结论

本文通过建立博弈模型，分析三种不同渠道权利结构下零售商增值服务水平和回收竞争强度对供应链中各成员最优决策的影响并进行比较。通过两阶段优化方法，得出三种不同权利结构下制造商和零售商的最优批发价格，零售价格和废旧产品回收率，并比较了三个不同博弈模型的最优值。

通过研究，本文得出以下结论：（1）整个行业以及消费者在都受益于无领导的市场结构；（2）即使所有最优解都受到竞争强度的影响，但并未改变三种权利结构模型下最优解的大小排序；（3）零售商增值服务水平对闭环供应链在不同权利结构下的制造商和零售商的定价和回收决策，以及渠道绩效有重要影响，然而在每一种博弈模型中存在一个服务水平上限，因此，零售商无限制提高服务水平的决策并不是最优的；（4）在Stackelberg博弈模型中，制造商和零售商都有动力成为领导者以获得更多利润；（5）与直觉相反，通过研究发现在三种博弈模型下零售商领导的Stackelberg博弈模型下的零售价格是最高的。