基于SARIMA模型和X-12-ARIMA季节调整方法预测的比较

李少雄，李本光

（1.中国工商银行北京分行，北京100031；2.贵州大学 经济学院，贵阳550025）

1 模型简介

1.1 SARIMA模型

SARIMA模型源于自回归移动平均模型（ARIMA模型）。ARIMA模型适用于非季节时间序列短期预测。对于季节时间序列，则需要进行正规差分、季节差分和自回归自动平均调整，才能转化为ARIMA模型。由这种方法最终所确认的ARIMA模型，由于通常包含季节差分的有关参数，同时由几部分的乘积形式构成，因此被称为季节乘积模型，即SARIMA模型。SARIMA模型的一般表达式为：

其中，d、D分别表示正规差分、季节差分，s为季节差分阶数，p是自回归阶数，q是移动平均阶数，ΦP(Ls)和ΘQ(Ls)分别为季节P阶自回归算子、季节Q阶移动平均算子，μt为白噪声过程。该模型可以简化为SARIMA(p，d，q)(P，D，Q)。

航空模型是季节乘积模型的具体表现形式，此模型广泛用于季度时间序列建模[1]。航空模型的表达式：

其中s是序列的周期，μt是白噪声序列，|θ|＜1，|Θ|＜1。航空模型的AR部分由正规差分和季节差分两部分组成，而MA部分包括两个参数。该模型具有一些显著的性质。假设Yt=(1 -L)(1 -Ls)Xt，ρ为Yt的样本自相关函数函数，则：

对于l＞0且l≠1，s-1，s+1，有ρl=0。因此，如果Yt是季节时间序列，Yt经过正规差分和季节差分后的序列的样本自相关函数只在滞后阶数为1、s-1、s、s+1时非零，那么可以考虑对季节时间序列Yt建立航空模型。

1.2 X-12-ARIMA季节调整方法

一个经济时间序列(Yt)受多种因素影响。通常可以把这些因素分解为趋势成分(Tt)、循环成分(Ct)、季节成分(St)和不规则成分(It)。季节调整就是对原始数据中隐含的由季节因素引起的影响加以纠正的过程。在季节调整模型方面，经典的时间序列模型有两种：

（1）加法模型Yt=Tt+Ct+St+It

（2）乘法模型Yt=Tt×Ct×St×It

按照加法模型，季节调整后的时间序列At=Tt+Ct+It；按照乘法模型，季节调整后的时间序列At=Tt×Ct×It。对于一个时间序列，采用哪种模型进行季节分解取决于各成分之间的关系。一般来说，若4种成分相互独立则采用加法模型，相互关联采用乘法模型；若季节因素的规模基本保持不变，不随原始序列水平的增减而变化，就使用加法模型；若季节因素的规模与原始序列水平成比例变化，使用乘法模型[2]。

在季节调整方法方面，X-11是国际上通用的季节调整方法。1980年，加拿大统计局在X-11季节调整方法的基础上引入ARIMA模型开发X-11-ARIMA程序，实现了序列向前、向后预测和补充数据，以保证移动平均季节调整过程中数据的完整性。20世纪90年代，美国普查局在X-11-ARIMA的基础上开发X-12-ARIMA程序。X-12-ARIMA能够对数据进行更加丰富的预处理，检测和修正不同类型的离群值，估计并消除日历因素的影响，对季节调整的效果进行更为严格的诊断检验。由于趋势成分和循环成分不容易分离，以上季节调整方法将趋势成分和循环成分视为一种成分进行分解和调整。通过对季节调整各分解因素的预测，可以实现对原始序列的预测。

2 实证

2.1 数据来源及相关说明

本文以贵州省1998—2015年固定资产投资季度数据为样本，分别建立SARIMA模型和使用X-12-ARIMA季节调整方法，对2016年固定资产投资季度数据进行预测，将预测值与实际值作比较，通过相对误差比较两种模型的精确程度。所有数据根据国家统计局网站贵州省固定资产投资月度数据整理而得，见表1。本文使用的操作软件为R语言，使用seasonal扩展包进行X-12-ARIMA季节调整，使用car扩展包进行DW自相关检验。

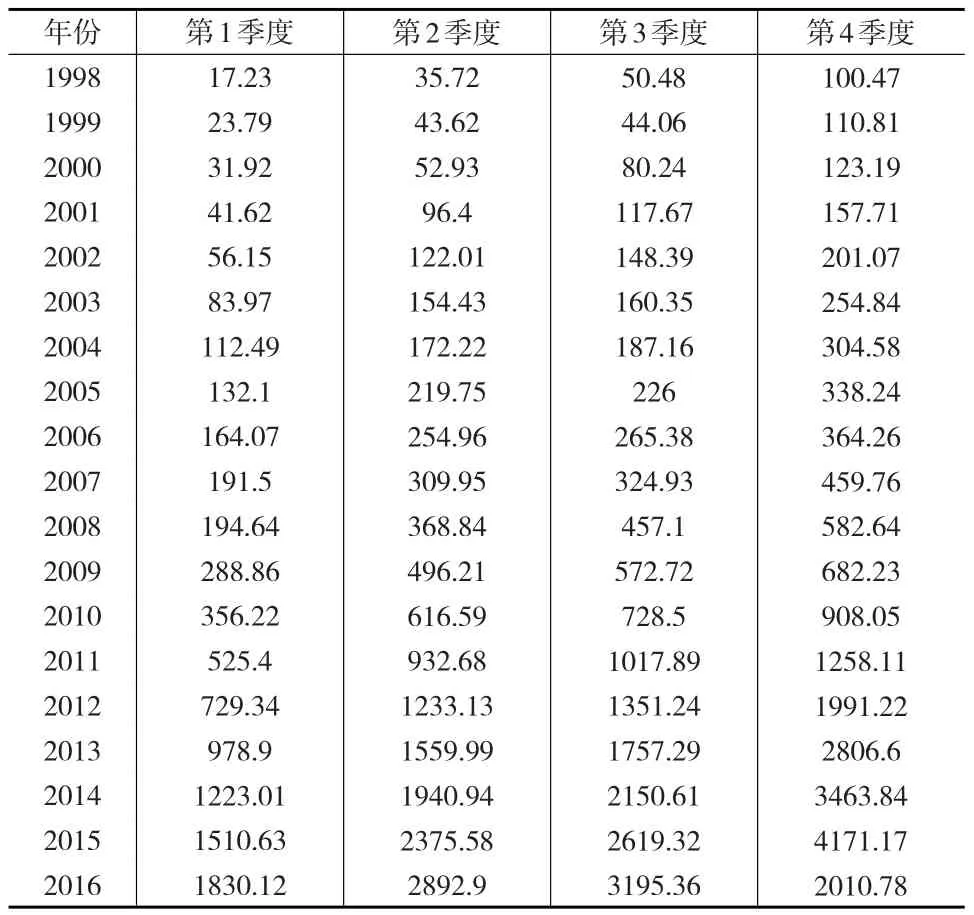
表1 贵州省固定资产投资季度数据

2.2 SARIMA模型分析

2.2.1 季节差分

首先对贵州省固定资产投资季度数据取对数，见图1。这里进行对数变换有两个原因：一是处理序列是指数增长。事实上，该时序图证实了取对数后的序列的确是线性增长的。二是稳定序列的波动。从图1中也能看出序列总体呈现直线上升的趋势，上下起伏震荡，序列不仅存在自相关还存在明显的的季节波动。因此可以采用季节乘积模型建模。

图1 贵州省1998—2016年固定投资季度数据时序图

图2 （a）表示对贵州省固定资产投资季度数据取对数后序列的自相关函数，从中可以看出取对数后贵州省固定资产投资季度数据序列具有明显的自相关性，是非平稳的。图2（b）表示的是对贵州省固定资产投资季度数据取对数后进行正规差分后的自相关函数，从中可以看出序列在季节滞后上的自相关系数不同于0值。图2（c）表示的是对贵州省固定资产投资季度数据取对数后进行季节差分后的自相关函数。图2（d）表示的是对贵州省固定资产投资季度数据取对数后进行正规差分后再进行季节差分后的自相关函数。

图2 样本自相关图

这里表at示残差序列。对于贵州省固定资产投资季度数据对数序列，该模型不充分，一个显著的原因是季节移动平均部分的系数在5%显著性水平下不显著。第二步，根据5%显著性检验，季节移动平均部分系数不显著，重新改进模型如下：

2.2.2 模型识别、建立和诊断

时间序列数据建模，数据仅仅是可利用信息的一部分。对所研究的问题，可能积累一些先验知识。在这种情况下，这些先验知识对于模型选择非常重要，可以把先验知识和数据结合起来进行交叉验证，不断改进模型。

对于贵州省固定资产投资对数序列，这里通过一个两步过程实现模型设定。第一步，建立初始模型。图2给出了贵州省固定资产投资对数序列的样本自相关函数图，虽然不完全满足航空模型样本自相关函数的表现，但是可以采用航空模型作为建模的初始模型，拟合结果为：

这里系数标准误差为0.0946，5%置信区间（-0.9568,为-0.5860）。虽然模型残差平方和略有增加，但参数通过了显著性检验，AIC值有所降低。图3给出了模型残差的一些检验图，残差在开始部分有个别异常值，但整体来讲，该模型是充分的。

图3 残差检验

2.2.3 预测

对未来4季度贵州省固定资产投资季度数据进行预测。为了得到2016年贵州省固定资产投资季度数据的预测值，而不是取对数后的值，这里需要利用正态分布与对数正态分布之间的关系，对预测值进行反对数变换，具体结果见表2。与实际值比较，可以看出，预测相对误差均很小，不超过4，说明模型预测具有一定准确性。但是相对误差均为正数，说明预测值具有偏大的倾向，容易过高估计未来固定资产投资季度数据。

表2 SARIMA模型预测

2.3 X-12-ARIMA季节调整方法分析

2.3.1 季节调整及原始数据的分解

为提取贵州省固定资产投资季度数据中的趋势成分、循环因素、季节成分和不规则成分，现通过seasonal扩展包直接对贵州省固定资产投资1998年第1季度至2015年第4季度当期季度数据进行季节调整。由于分解因素相互关联，且季节成分随原始数据规模增长而增加，因此在X-11季节调整过程中采用乘法模型。由于X-11体系的季节调整程序将趋势成分和循环成分视为一种成分，因此这里按照加法分解模型将贵州省固定资产投资季度数据分解为趋势-循环因素(TCt)、季节因素(St)和不规则因素(It)三种成分。考虑到原始数据的指数增长特性和较大的季节波动性，在季节调整过程中取对数变换。在季节调整过程中，自动识别1999年第3季度、2000年第2季度、2008年第1季度3个离群点，如图4所示。通过季节调整，分别得到分解成分，如图5。

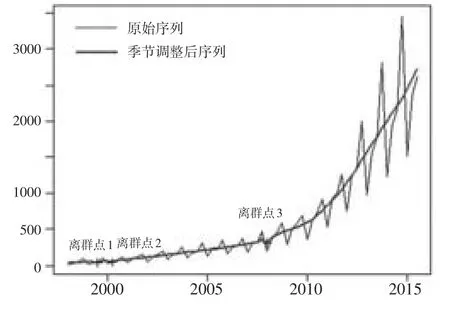
图4 原始序列和季节调整后序列

2.3.2 趋势-循环成分的预测

原始数据经过季节调整之后，依然保留有趋势-循环成分。这时可利用回归分析的方法对其进行拟合和预测。观察图5可知，随着时间的变化，季节调整后固定资产投资呈现上升的趋势，总体数据同样呈现曲线增长的趋势。由于曲线难以完全用抛物线和对数曲线拟合，在这里截取2010年第2季度至2015年第4季度共22个样本点采用抛物线重新拟合，以时间t为自变量，以季节调整后的FAI数据为因变量，拟合结果为：

图5 季节调整分解图

采用car扩展包进行DW自相关性检验，DW统计量为1.7369，p值等于0.422，不能拒绝原假设，因此不存在显著的自相关性。可以预测2016年4个季度固定资产投资趋势-循环成分，结果见表3。

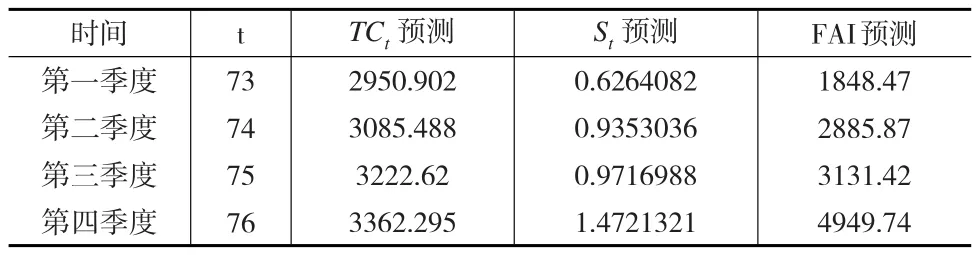
表3 FAI的预测过程和预测值

2.3.3 季节成分的预测

从图5中看出，季节因子具有不稳定的特性。罗中德（2016）[3]采用规范化的方法计算季节指数，将其作为下一年度季节因子的预测值。本文假设季节因子不变，直接截取2015年4个季度的季节因子作为2016年4个季度的季节因子进行预测，结果见表3。

2.3.4 对季度数据的预测

由于不规则成分样本自相关函数、偏自相关函数不具有截尾特征，在滞后10阶通过了Q检验，因此可以不考虑不规则成分变动的影响,直接采用公式Yt=TCt×St预测2016年贵州省固定资产投资季度数据。2016年贵州省固定资产投资季度数据的预测值等于2016年固定资产投资趋势-循环预测项与季节因子预测项两项的乘积。具体结果见表3。

2.4 模型比较

两种方法对原始数据都有比较好的预测效果。SARIMA模型采用ARIMA乘积的形式对季度数据进行拟合和预测；X-12-ARIMA将原始时间序列分解，分别对分解成分进行预测，对数据的处理更加完善。从预测精度上看，SARIMA模型预测的相对误差在2%～4%之间；而X-12-ARIMA季节调整方法的相对小于2%。值得注意的是，SARIMA模型预测的相对误差都大于零，预测值具有大于实际值的趋势，而X-12-ARIMA季节调整模型的预测值的相对误差在零附近波动，有正有负，相对误差率更小且合理。表4（见下页）为两种预测的比较。

表4 模型比较

3 结束语

固定资产投资时间序列主要是受到趋势性和季节性的影响，目前主要采用ARIMA或者SARIMA模型进行预测。SARIMA模型具有较高的预测精度，但是随着时间序列数据跨期增多，长期预测结果不理想；且从预测结果来看，其预测值具有被高估的倾向。故可以采用X-12-ARIMA季节调整方法进行预测，其预测值更加精确合理。