基于最优脉冲的面内机动规避策略
苏飞,刘静,张耀,杨旭
(中国科学院国家天文台,北京100012)
1 引言
随着空间技术及商业小卫星的发展,空间碎片数量急剧增加、空间环境迅速恶化,根据最新资料显示,目前在轨10cm以上空间碎片数量达到2万个[1-3]。密集的空间碎片对航天器的在轨运行产生巨大威胁,急需制定策略应对航天器的危险交会,航天器轨道机动规避在躲避碎片碰撞时直接有效,受到航天机构及卫星运行商的广泛关注[4-5]。航天器进行规避机动时,一方面需要考虑风险的消除程度,另一方面则需要分析机动对航天器运行的影响。
国内外学者对航天器机动规避的动力学与控制问题进行了广泛的研究,同时根据不同的优化目标、优化算法提出多种机动规避策略,并对部分研究成果进行了飞行验证。Chan[6-7]研究了一般推力得到碰撞概率和推力的解析表达,结合航天器轨道控制研究规避机动;Kim等[8]分析了基于遗传算法的燃料消耗和机动时长,采用多目标优化求解碰撞规避机动策略;Bombardelli等[9-10]根据轨道机动规避动力学模型,推导了机动脉冲与碰撞概率的解析关系,通过拉格朗日乘子法得到固定脉冲的最优方向;Patera等[11-13]基于一维碰撞概率积分方法推导速度增量的最优解,采用两体轨道积分代替高精度轨道积分研究碰撞规避机动策略;Kelly等[14]利用非线性规划算法求解最小速度增量,得到最优的碰撞规避机动策略;Peterson[15]对近圆轨道提出了可以快速得到推力三维解的解析方法,利用梯度搜索算法找到最优解;王华等[16]基于碰撞概率分步求解机动方向和机动大小,在碰撞概率降低到安全值的前提下得到最优的避撞机动冲量;Gavin[17]利用根数长期项分析了初始轨道根数与危险交会点的关系,研究了卫星冲量对交会点的影响;Alfano等[18-19]研究了执行机动导致的额外风险和燃料消耗对航天器任务的影响。
目前多数已有研究成果在研究航天器机动规避时,主要基于数值法穷举寻优,未关注计算效率问题,事实上危险交会往往具有突发性,对时效性要求较高。为了快速得到优化的规避脉冲,首先通过小偏差线性化等处理将高斯方程解析化,得到解析的轨道规避机动动力学模型,直接分析机动脉冲与航天器相对运动的线性关系。通过航天器位置协方差信息及交会平面的相对位置信息得到航天器危险交会的碰撞概率和交会距离,并采用固定脉冲的方式,快速得到最优机动方向,获取不同时机下的最优脉冲。
2 规避动力学模型
2.1 建模假设
在空间物体碰撞预警过程中,如果危险交会的瞬时碰撞概率或交会距离大于安全阈值,经检测确认为危险交会后,航天器需要进行机动来规避风险,保证运行安全。在执行规避时,很多空间环境的影响相对于机动量可以忽略不计,所以建模过程做如下假设:一是地球为质地均匀的球体,并忽略大气阻力、太阳光压等所有摄动力;二是机动脉冲为小量,机动后航天器到达危险交会点的速度大小及方向不变;三是交会物体位置误差椭球固定,不随机动变化;四是交会为短期交会,交会时航天器视为匀速直线运动,且不考虑姿态。
2.2 坐标系定义
相关动力学建模参照坐标系如图1所示,其中OXYZ偏心率矢量坐标系,其原点O位于地球质心,X轴与航天器偏心率矢量eo重合,Z轴垂直于航天器轨道平面,且与航天器角速度方向相同,Y轴由右手螺旋法则确定;sxyz为航天器轨道坐标系,其原点s位于航天器质心,x轴由地心指向航天器质心,z轴与Z轴平行且指向相同,y轴由右手螺旋法则确定,三轴单位矢量分别为ex、ey、ez。
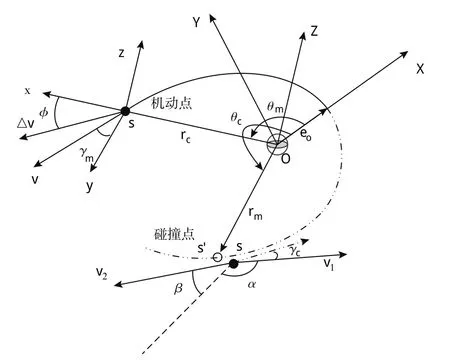
图1 建模参照坐标系Fig.1 Reference coordinate system for modeling
2.3 机动动力学模型
如图1所示,航天器在偏心率矢量坐标系的状态矢量表示为

式中,eX和eY为偏心率矢量坐标系对应坐标轴的单位矢量;a为航天器轨道半长轴;E为航天器对应真近点角处的偏近点角;e为航天器轨道偏心率;r为航天器地心距;μ为万有引力常数。
令E=Em,取惯性系内航天器机动点即真近点角为θm处的状态rm、vm代入式 (1),求解方程式得
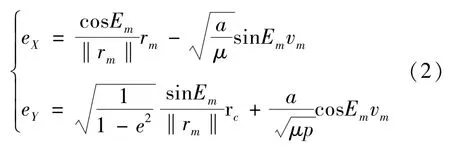
式 (2)中符号‖‖表示对矢量求模,将式(2)代入式 (1)得偏近点角为E处航天器的位置矢量r表示为

结合高斯方程,冲量使航天器轨道产生的瞬时变化为

式中,Δvx、Δvy、Δvz分别为冲量在航天器轨道坐标系三轴上的分量,h、p分别为航天器变轨前的轨道角动量和轨道半通径,表示为

将航天器的状态量代入式 (3),则航天器在机动点θm处机动前和机动后,运行到危险交会点的位置矢量r(Ec)、r′(Ec)分别表示为

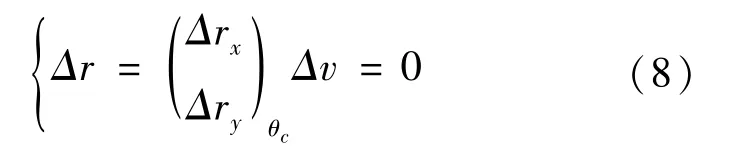
式中,Δrx、Δry分别为航天器在轨道系中相应坐标轴的位置变化,由于航天器机动后,其偏心率矢量坐标系绕Z轴转动Δω,将式 (6)、式(7)表示到机动前的偏心率矢量坐标系,则

其中

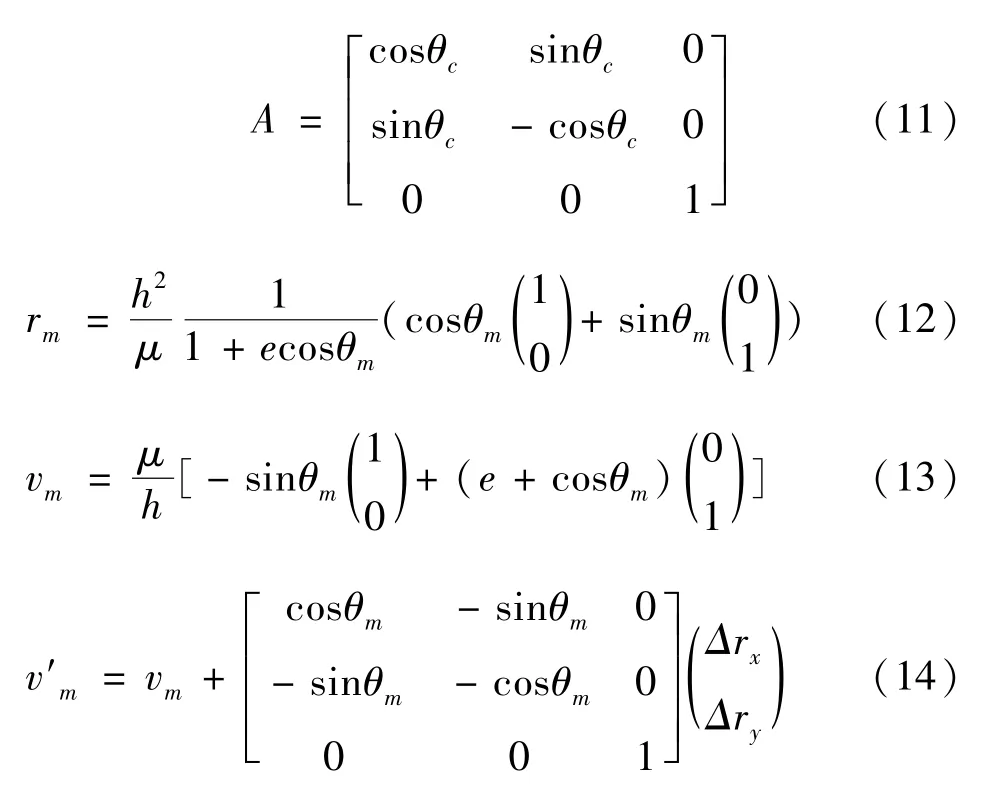
为了推导方便同时减小因量级的巨大差异引起的仿真失真,进行归一化处理,定义

将式 (10)~式 (14)代入式 (9)并泰勒展开,由于脉冲大小远远小于航天器速度,省略高阶项,推导过程不再赘述,这里直接给出表达式,得径向距离的变化和沿迹方向的距离变为分别为[10]

式中
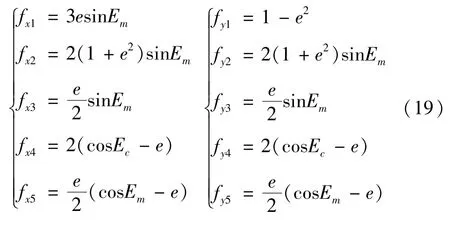
从动力学模型可以看出,在机动脉冲为小量时,航天器机动导致的距离变化可以简化为航天器轨道参数的解析表达,与外推模型相比可以大大节省计算时间,并能得到机动大小与距离变化的等式关系,有利于模型的物理分析和控制参数选取。
3 航天器危险交会分析
航天器危险交会过程中通常采用交会距离判定法或碰撞概率判定法来判断发生碰撞的可能性。碰撞概率判定法适用于两星的定位误差较大且有累积效应时,交会距离判定法则适用于能实时测量两星相对状态。
3.1 交会距离
航天器运行时,设s(t)为t时刻航天器s-1与s-2的相对位置矢量,则任意时刻t+Δt两个目标的相对位置矢量为
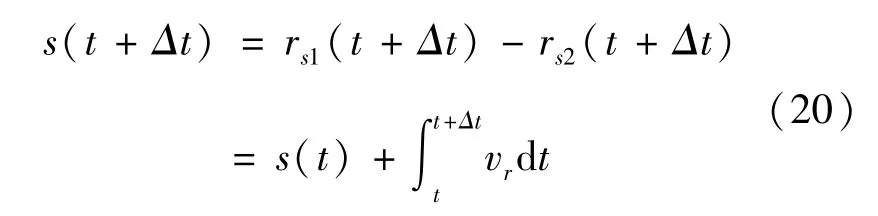
其中vr=v1-v2,若t时刻两目标间的距离最小,则有
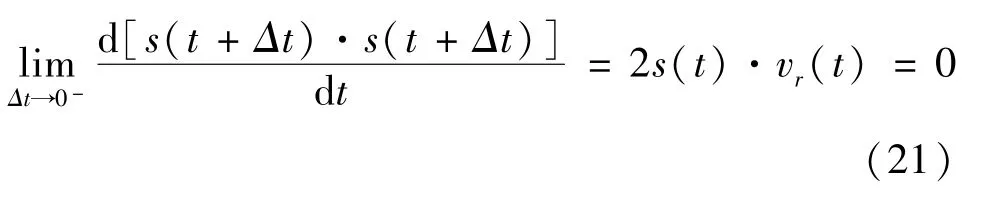
根据式 (21)得两目标距离最小时,其相对位置矢量和相对速度矢量互相垂直。定义交会坐标系,其三轴单位矢量分别为

航天器相对运动方向平行于x轴,交会平面(b平面)定义为y-z平面,则航天器危险交会关系描述为两航天器在b平面的交会距离,航天器轨道坐标系到交会坐标系的转换矩阵为

式中,α为危险交会点处s-2速度矢量v2在s-1轨道面投影与s-1速度矢量v1的夹角 (-π<α<π),且v2×v1·eZ>0时为正;β为v2在航天器s-1轨道面投影与v2的夹角 (-π/2<β<π/2),且v2·eZ>0时为正;B为v1与相对速度v1-v2的夹角 (0 交会距离为 航天器在运行过程中位置误差服从3维正态分布,并可以通过分布中心和位置误差协方差矩阵描述。此时航天器间交会的碰撞概率均可表示为 式中,V为以一个航天器为圆心,两个航天器包络半径之和ssum为半径的球体;f(x,y,z)为高斯概率密度函数 (PDF),表示为 式中,se=(xbm,0,zbm)为b平面内两航天器交会距离最小时的相对位置矢量;为相对位置s误差协方差矩阵C的行列式值,假设航天器交会时为匀速直线运动,则积分球变为圆柱,在误差协方差矩阵中选取与相对位置信息有关的部分得 此时碰撞概率表示为圆域内的积分 文献 [7]提出一种不等方差PDF在圆域内积分问题的解决方法。通过将不等方差的等概率密度椭圆用与其面积相等的等概率密度圆代替,并用无穷级数表示二重积分,对式 (30)简化得到碰撞概率的解析表示 其中u和v均为无量纲变量,表示为 通过求碰撞概率/交会距离对于机动方向的梯度确定机动速度方向。 机动方向可以通过梯度矢量D得到 式中,D表示为 由于碰撞概率/交会距离的梯度与机动脉冲大小不相关,对轨道面内的脉冲做如下变形 式中,为归一化的机动脉冲大小,视为固定值;φ为脉冲矢量与轨道系x的夹角。此时交会距离的平方表示为 当确定交会目标的Ec、Em、e,最优交会距离值所需要的机动脉冲速度方向即为下式的解 机动方向可以通过梯度矢量D′得到 式中,D′表示为 此时碰撞概率相关系数描述为 当确定交会目标的Ec、Em、e,最优碰撞概率所需要的机动脉冲速度方向即为下式的解 根据上述理论建模与分析的结果,建立航天器规避机动数值仿真模型和航天器危险交会分析模型。为了验证所设计的规避机动策略的有效性,本节利用美俄卫星碰撞事件为例进行仿真。Cosmos-2251和Iridium-33中,前者为俄罗斯的废弃卫星没有任何机动能力,后者为美国的在用通信卫星可以执行规避机动,选择两颗卫星碰撞前的各自最新的一组TLE根数,利用SGP4轨道预报模型,可知两颗卫星TCA的参数如表1所示 表1 美俄卫星碰撞交会几何参数Tab.1 Collision rendezvous geometry parameters of the US and Russian satellites 根据Cosmos-2251和Iridium-33的预报数据,相对位置s误差协方差矩阵假设为对角协方差矩阵,其标准差在航天器相对运动切线方向为1km,在b平面内的两个正交方向上为100m,此时在误差协方差矩阵中与相对位置信息有关的部分为[9] 航天器机动规避过程需要考虑轨道维持要求,Iridium-33属于低轨道卫星,受空间环境因素影响较大,在轨运行期间轨道衰减与星下点漂移现象明显,需要定期进行轨道维持,以保证星下点相邻轨迹的无缝搭接。图2为航天器星下点轨迹保持环,即地面轨迹保持范围及半长轴变化过程构成一个封闭的环。 图3是航天器机动规避时不同机动提前量下的最优交会距离,从图可得在提前量不是整数周期或不靠近整数周期时,提前机动时间越大,得到的最优交会距离越大;提前量为整数周期提或在其附近时,最优交会距离回落,稍有减小。 航天器执行机动规避时,通常需要考虑轨道维持,即需要在避碰的同时完成轨道抬高,所以在仿真过程中,取脉冲方向与轨道系x轴夹角为0≤φ≤π,图4是最优交会距离约束下航天器机动规避时不同机动提前量下的最优脉冲方向,从图得航天器规避提前量在0到0.2周期时,最优脉冲方向收敛至180o(0o),提前量超过约0.2周期后,最优脉冲方向收敛至90o附近。 图2 航天器星下点轨迹保持环Fig.2 Spacecraft ground track keeping ring 图3 不同机动提前量时的最大交会距离Fig.3 Maximal rendezvous distances with different maneuver leads 图5是航天器机动规避时不同机动提前量下的最优碰撞概率,与最优交会距离分析类似,从图可得在提前量不是整数周期或不靠近整数周期时,提前机动时间越大,得到的最优碰撞概率越小;提前量为整数周期提或在其附近时,最优碰撞概率振荡且稍有增大。 图4 不同机动提前量时的最优脉冲方向Fig.4 Optimal pulse directions with different maneuver leads 图5 不同机动提前量时的最优配置概率Fig.5 Optimal configuration probabilities with different maneuver leads 图6 不同机动提前量时的最优脉冲方向Fig.6 Optimal pulse directions with different maneuver leads 取脉冲方向与轨道系x轴夹角为0≤φ≤π,图6是最优碰撞概率约束下航天器机动规避时不同机动提前量下的最优脉冲方向,从图得航天器规避提前量在0到0.25周期时,最优脉冲方向收敛至180o(0o),提前量超过约0.25周期后,最优脉冲方向收敛至90o附近。 研究了航天器面内机动规避最优问题。针对高斯方程,利用小偏差线性化及泰勒展开得到轨道规避机动动力学模型,基于面内机动约束,在保证碰撞概率降低到最小值或交会距离提高到最大值的前提下得到最优的机动脉冲。为机动规避的工程问题提供支持。

3.2 碰撞概率
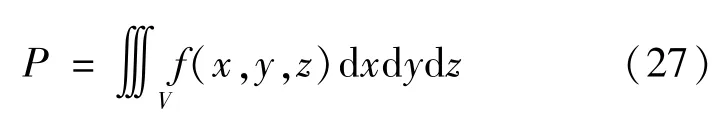





4 最优规避分析
(1)交会距离最优问题描述为


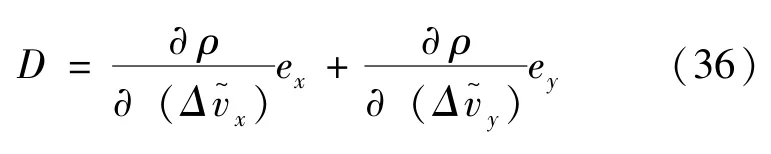



(2)同理,碰撞概率最优问题描述为
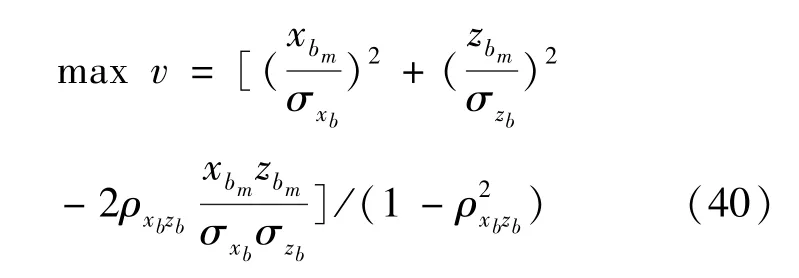




5 仿真分析及校验

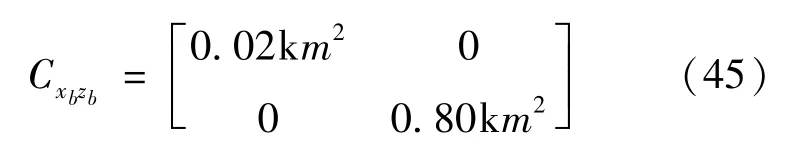





6 结论

