火箭末级电动绳系离轨动力学建模与分析

翟光,宋国梁,杨少伟

(北京理工大学宇航学院,北京100081)

1 引言

近年来,空间碎片的主动移除技术逐渐受到各国航天机构的关注[1-2],国内外许多学者提出并研究了不同的空间碎片主动移除方法[3]。采用电动绳系 (Electro-Dynamic Tether)对空间碎片实施离轨操作,具有无需燃料消耗的特殊优势,因此受到了各国重视。针对电动绳系离轨过程的控制问题,国内学者张健[4-5]等人研究了电动绳系轨道运动与绳系运动的耦合问题,并采用结构设计方法,提出了解耦控制策略;针对电动绳系横线振动问题,徐大富[6-7]通过建立电动绳系的偏微分方程和边界条件,采用有限元方法分析了系统的横向振动规律;电动绳系的自主离轨速率是较多学者关注的问题,Steven G[8]等人在控制电流变化的基础上,设计了电动绳系轨道机动的变轨控制策略;R.Zhong[8]基于高斯摄动方程建立了电动绳系纳星系统的轨道动力学模型,并分析了在不同轨道倾角条件下系统的离轨特性。Claudio[9]建立了电动绳系离轨时间的理论计算模型,并结合第十一代国际地磁场模型进行了仿真验证。然而,由于受安培力长期作用,电动绳系的轨道和姿态运动存在严重耦合,安培力矩可通过改变姿态运动的方式,直接影响电动绳系的轨道变化速度。在目前已有文献当中,多数学者均在假设绳系方向与轨道矢径平行的基础上,开展相关建模与分析工作,但事实上,在不施加控制的条件下,电动绳系与轨道矢径方向存在着夹角,且是动态变化的,因此,其离轨过程运动特性分析结果具有较大的误差。

本文针对火箭末级等大型空间碎片离轨问题,在考虑安培力矩的基础上,首先建立电动绳系释放过程的非线性姿轨耦合动力学模型,充分反映了加电之后安培力对电动绳系姿态运动的影响,随后结合第十一代国际地磁场模型,建立了电动绳系离轨过程的动力学数值仿真模型,并通过仿真分析了离轨过程中电动绳系姿态和轨道变化情况,由此获得了不同初始轨道条件下电动绳系系统的离轨时间。

2 电动绳系姿轨耦合动力学建模

2.1 建模参考坐标系

首先建立电动绳系的轨道坐标系和本体固连坐标系。如图1所示,轨道坐标系原点位于系统的质心,xo轴和zo轴分别指向系统轨道速度方向和地心方向;本体固连坐标系为最大主轴惯量坐标系,原点固连于系统的质心,zb轴由飞行平台质心指向末端质量质心,xb轴方向由式 (1)确定,yb轴根据右手螺旋法则确定。

建模作如下假设:重力场为理想的中心力场;忽略地球扁率和空间环境摄动因素的影响;火箭末级和末端质量均为质点,电动绳系末端2个连接点都位于连接对象的质心。

图1 电动绳系动力学建模参照坐标系Fig.1 The EDT reference frame for dynamic modeling

2.2 系统的动能

如图2所示,根据质心的定义有:

将上式中x替换为y、z亦成立。式 (2)中m为末端质量大小,M为火箭末级质量,ρ电动绳系的线密度,l∗、l为电动绳系总长度和展开长度;x1和x2分别火箭末级和末端质量为在轨道坐标系内的x轴坐标分量。

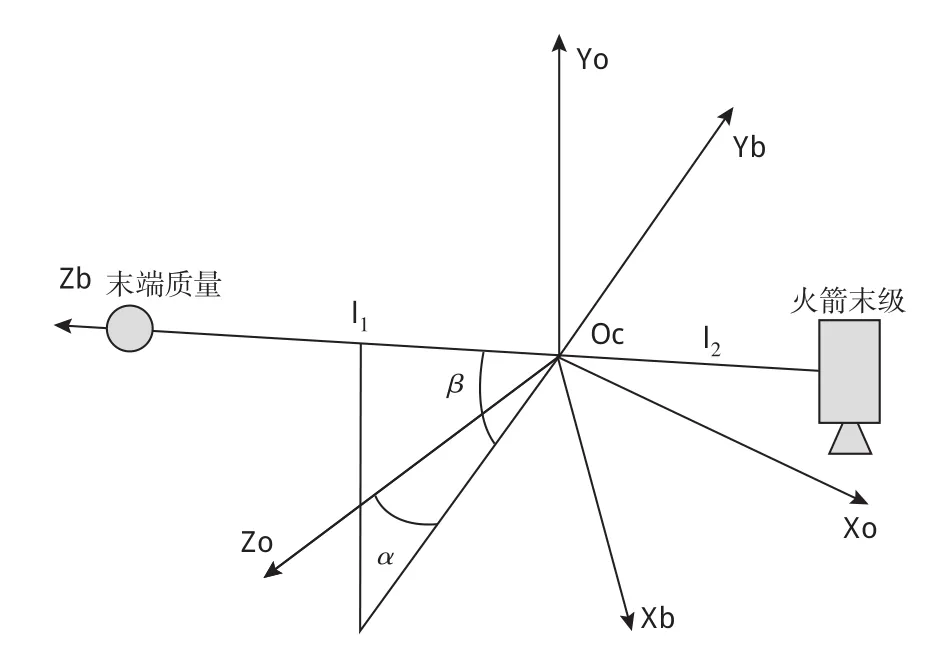
图2 电动绳系构型示意图Fig.2 The configuration of EDT system

根据质心定义可得:

电动绳系在释放过程当中,整个系统的动能由3部分组成,其中包括系统质心沿轨道运动所产生的动能T1;系统绕质心转动所产生的动能T2;连接电动绳系长度变化所产生的动能T3。为节约篇幅,推导过程不再赘述,这里直接给出表达式如下:

2.3 系统的势能

对于质量微元dm,其在重力场中的势能为:

末端质量和火箭末级的势能可分别表示为:

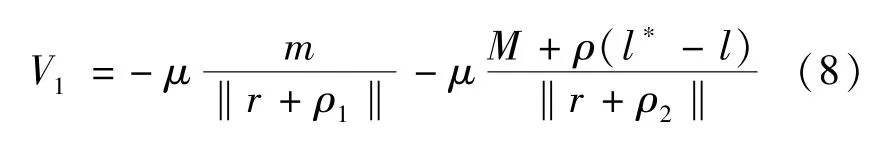
μ为地球引力常数,ρ1和ρ2两段绳系在轨道坐标系内的矢量,r表示轨道坐标系内的轨道位置矢量,根据2质点在轨道坐标系中的位置关系,并忽略高阶项,对式 (8)分母部分进行泰勒展开,则有:

式中,r=‖r‖,α和β分别表示电动绳系的面内外摆角。将式 (9)和式 (10)代入到式(8)中,由此可以得到火箭末级和末端质量的势能函数,其表达式可以表示为

采用同样的方法可以得到电动绳系的势能函数为:

此外,在实际电动绳系释放过程当中,电动绳系在一定的拉伸作用下发生弹性变形。引入电动绳系的应变系数ξ,E为电动绳系的弹性模量,A为横截面积,则系统的弹性应变势能可以表示为:

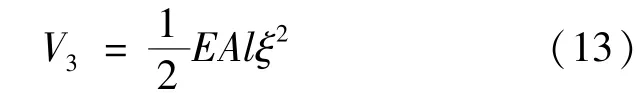
系统总势能函数可由V=V1+V2+V3计算得到。

2.4 系统的拉格朗日函数

根据拉格朗日定理,系统的拉格朗日函数为:

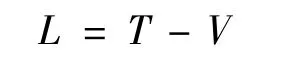
将系统的动能函数和势能函数代入上式可得系统的拉格朗日函数具有以下的形式 (见式14):

由于模型考虑了电动绳系的质量,系统的拉格朗日函数十分复杂。在实际的工程当中,由于电动绳系质量远远小于系统其他部分质量,因此可以忽略不计,即可认为ρ=0,此外,忽略系统的柔性,此时拉格朗日函数中的弹性势能项可略去不计,进一步定义归一化广义外力:

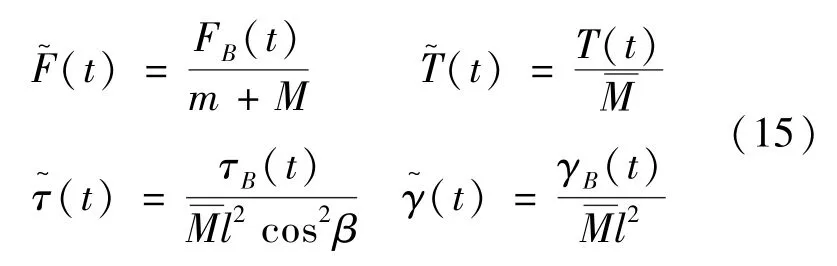
式中,FB(t)、τB(t)和分别表示广义外力和外力矩,其中包括安培力和力矩。根据拉格朗日定理,按式 (12)对拉格朗日函数中的广义坐标求导,

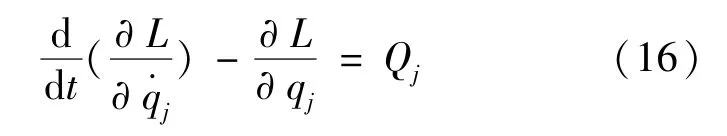
式中,qj和Qj分别表示广义坐标和广义外力,则可导出系统的刚性动力学模型为:

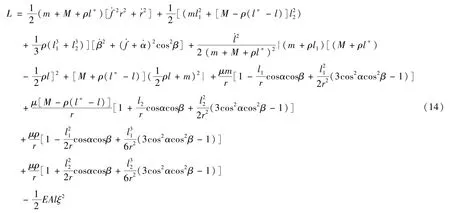
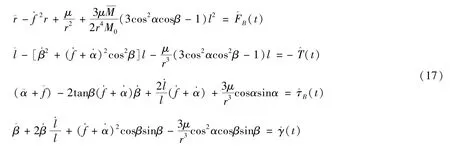
动力学方程是在连接电动绳系刚性假设的情况下推导建立的,而系统的刚性假设只有在连接电动绳系处于张紧状态的时候才能够成立,若电动绳系处于松弛状态时,末端质量和火箭上面级之间的动力学耦合关系不再成立,即式能够描述系统动力学特性的前提条件是连接电动绳系处于张紧状态,即T^(t)>0。

2.5 模型的轨道面内外运动解耦

观察式(17),当β和β·的初值为零时,其他3个变量方向上的运动并不会诱发面外摆角的运动,当忽略面外摆角后,模型可以进一步简化,其中刚性动力学模型可以简化为:

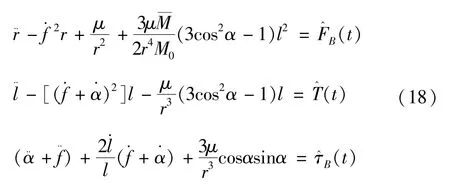
在不考虑安培力的条件下,式 (18)中第1个方程可以表示为

方程中左侧第2项为扰动项,这说明电动绳系长度或者姿态变化时,会带来实际轨道相对于开普勒轨道的偏移。严格意义上来讲,电动绳系系统质心的轨道并不是精确的开普勒轨道,但是由于扰动项很小,在短时间运动过程当中可以忽略不计。

3 系统的振荡运动

3.1 基本模型

国际参考地磁场 (IGRF)是描述地球主磁场空间结构和时间变化的通用模型。地磁场磁位势满足拉普拉斯方程,它在球坐标系中用球谐函数表示:

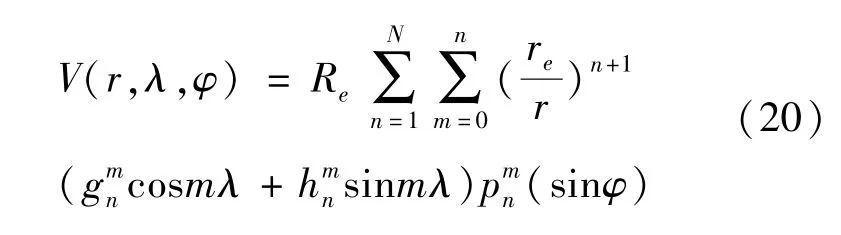
地磁场强度B为磁势函数V的负梯度,即

式中,re为地球参考球赤道半径;r、λ、φ分别为 EDT的地心距、地心经度和纬度;Pnm为schmidt函数;为磁场球谐函数的系数,IGRF模型提供相应的高斯系数表;为n次m阶schmidt准归一化缔合勒让德函数。

我国《国家安全法》第52条规定：“国家安全机关、公安机关、有关军事机关根据职责分工，依法搜集涉及国家安全的情报信息。”特别在第四章第二节“情报信息”第51条～第54条中，分别规定了“情报工作制度”“各部门搜集上报情报信息职责”“情报信息工作运用现代科技手段和加强研判分析”“情报信息的报送要求”等内容。“该法的立法模式呈现‘原始型’（即分散式立法）向‘混合型Ⅰ’（即分散式＋专门式立法）再向‘混合型Ⅱ’（即分散式＋专门式＋综合式立法）发展的趋势”。《国家安全法》是我国国家安全领域的基础性法律，也是统筹、引领国家安全领域立法工作的综合性法律之一，该法涵盖了国家安全多个领域。

3.2 地磁场倾斜偶极子简化模型

n=1、m=1时称倾斜偶极子模型。本文考虑了磁轴中心与地球中心不重合的状况,采用了偏心倾斜偶极子模型,此时磁场强度在惯性系下为:

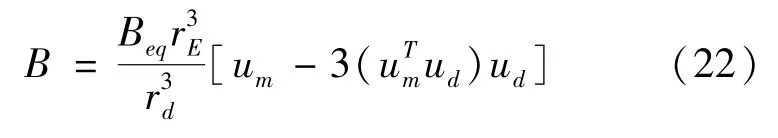
式中,Beq是偶极子模型中rE处的磁场密度;um是磁偶极子单位矢量;rd是EDT相对于磁偶极子中心的距离,ud是EDT相对于磁偶极子中心的单位矢量。磁偶极子密度Beq可以直接由高斯系数表示为:

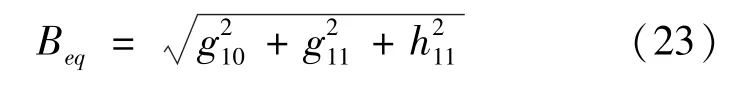
若初始时刻磁偶极子轴在地心惯性坐标系的x-z平面内,那么磁偶极子单位矢量为:

其中Ω是地球自旋角速度;β是磁偶极子轴相对于地球自转轴的倾斜角,对于倾斜偶极子模型,其值可以由下式得到:

根据2015年的国际参考地磁场模型,磁偶极子中心在地心地固坐标系的坐标 (单位是km)以及偶极矩向量的经度为:

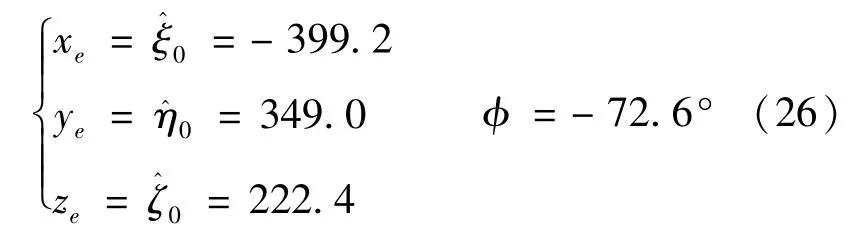
根据高斯定理,它们由下列各式求得:

磁偶极子中心在赤道惯性坐标系内可以表示为:

其中:

式中,rsc为EDT在惯性系内的位置矢量。

4 电动绳系轨道运动分析

4.1 安培力作用下的轨道摄动

电动绳系系统轨道动力学方程为:

式中,r是位置矢径,v=;fe为安培力摄动下的加速度。电动力缆绳穿过地磁场,可以产生的电流大小为:

缆绳系统的总电阻为R,电流在地磁场中的运动感应产生作用于缆绳的洛仑兹力为:

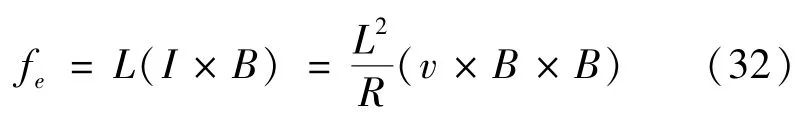
将式 (32)式代入式 (31),最终得到电动绳系在安培力作用下的摄动方程:

4.2 安培力矩作用下的面内姿态摄动

用Tio(t)表示惯性系到轨道坐标系的矢量转换矩阵,在轨道坐标系内,则缆绳的长度矢量在轨道,面内分量可表示为:

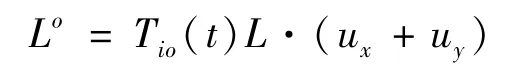
电动绳系所受安培力可进一步在轨道坐标系内表示为:

该矩阵是关于时间的函数,可根据电动绳系的轨道运动进行计算获得。则安培力在轨道平面的分量可在轨道坐标系内表示为:

则安培力在轨道面内的摄动力矩可表示为:

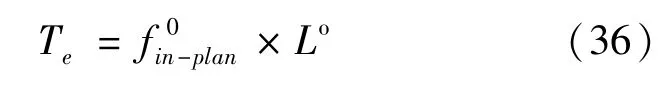
结合式 (15)和式 (18),则电动绳系轨道面内姿态摄动方程可以表示为:

观察式 (35)可以看到,当电动绳系完成释放且达到平衡之后,有:

整理之后则有:

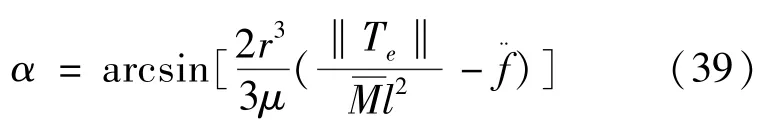
式 (39)说明,在无控的条件下,电动绳系和当地垂线方向存在夹角,且该夹角是动态变化的。

5 考虑缆绳姿态的离轨仿真验证

本部分结合火箭末级离轨任务,建立了电动绳系离轨过程的数值仿真模型,仿真模型将系统轨道动力学、地磁场模型和绳系动力学三者结合到一起,在综合考虑缆绳的面内姿态摆动的条件下,验证电动绳系的离轨效果。需要说明的是,本仿真模型当中暂未考虑地球形状摄动、大气阻力摄动等因素,以第十一代地磁场模型为参照,建立地磁倾斜偶极子数值模型。电动绳系的参数如表1所示。

表1 EDT仿真参数Tab.1 Parameters for EDT simulations

假设绳系以初始速度1m/s,在600km高圆轨道,沿轨道半径方向释放过程面内构型变化情况,释放过程中电动绳系未加电,因此无安培力和力矩作用。根据式 (18),由于绳系长度发生变化,因此在释放过程,面内摆角开始逐渐增大,当完成释放之后,电动绳系仍然在面内作周期性摆动,这充分说明绳系在释放过程必然会偏离轨道半径方向,因此在分析其离轨过程时,假设绳系始终和当地垂线方向重合必然导致明显的分析误差。为说明考虑电动绳系面内姿态摆动的必要性,本文分别在考虑和不考虑面内姿态变化的情况下,对其离轨效果做了仿真对比,仿真周期为1天。

图3是1天之内电动绳系所处地磁场强度的变化情况。图4是1天内电动绳系轨道高度变化情况。仿真结果说明,两种情况下1天降轨高度相差大约180m左右。图5是电动绳系从不同初始轨道高度降低至400km所需要的离轨时间,其中 ‘∗’和 ‘×’分别表示考虑和不考虑面内摆动的结果,可以看到,两者离轨时间最大相差近5天。当初始轨道高度增加时,离轨时间偏差也会进一步增大。

图3 EDT 24h内所处地磁场矢量的变化Fig.3 Earth magnetic field vector for EDT during 24 hours

上述两种情况之所以降轨高度不同,是因为两种情况下电动绳系生成的电压不同,进而导致安培力不同,图6和图7分别是两种情况下电压和安培力加速度变化情况,可以看到,两种不同的仿真条件对应的仿真结果具有明显差别。

图4 EDT 24h内轨道高度变化Fig.4 Orbit altitude change during 24 hours for EDT

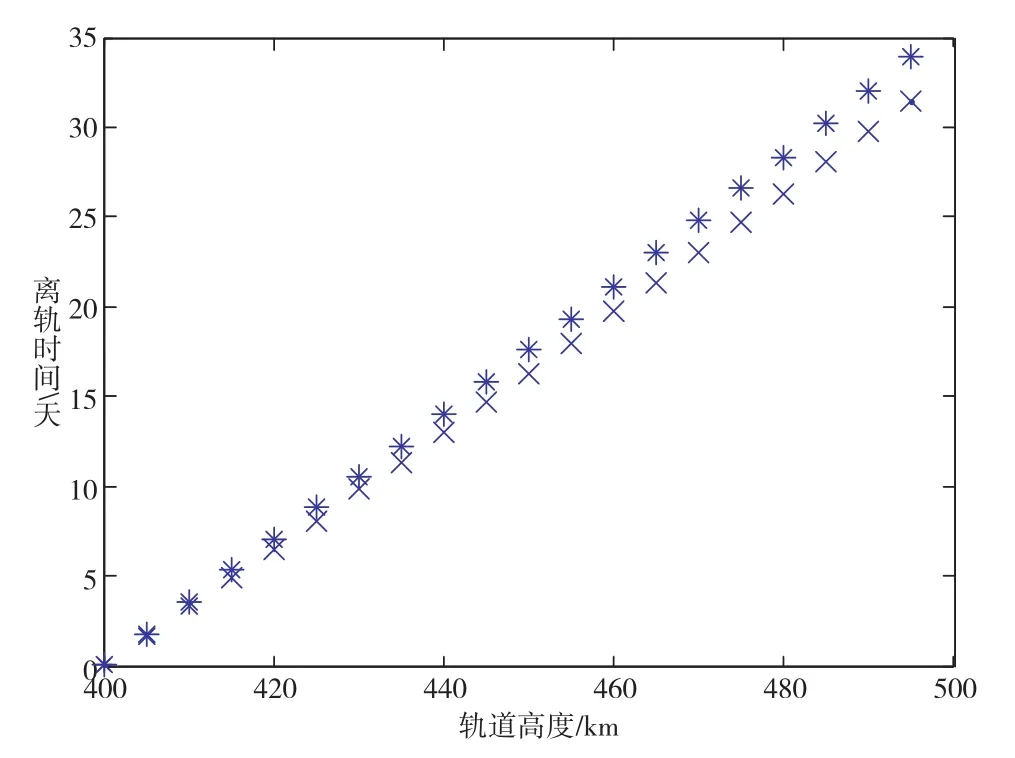
图5 不同初始轨道的离轨时间变化Fig.5 Deorbit time for different initial orbits

图6 EDT 24h内电压变化情况Fig.6 EDT Voltage history during 24 hours

图7 EDT 24h安培力加速度变化Fig.7 EDT acceleration by Ampere force during 24 hours

图8和图9是在600km高,轨道倾角为0°和45°情况下,2天内电动绳系面内摆角以及面内摆角加速度大小的变化情况,其中面内摆角加速度的大小说明了电动绳系所受安培力矩的大小。图9和图10仿真结果说明,电动绳系在轨运行过程当中,在重力梯度力矩和安培力矩综合作用下,面内摆角和所受安培力矩都是动态变化的。

图8 i=0°时面内振荡情况Fig.8 In-plane libration for i=0°

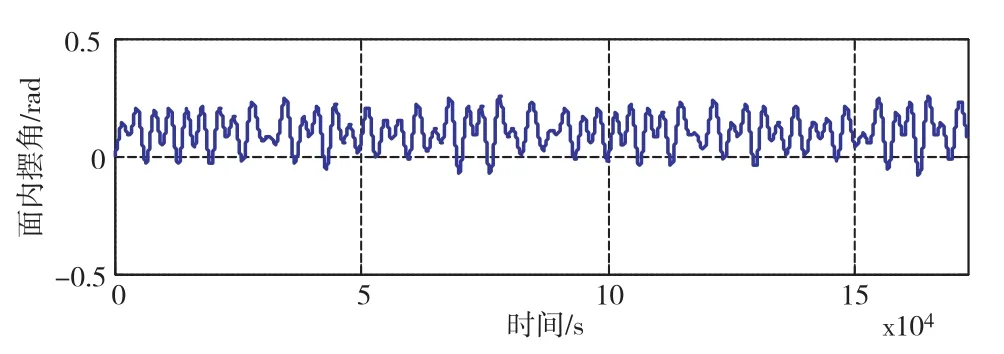
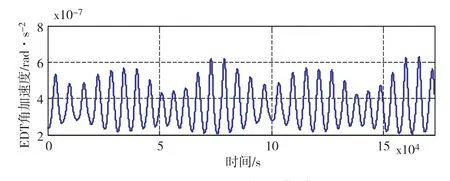
图9 i=45°时面内振荡情况Fig.9 In-plane libration for i=45°

6 结 论

采用拉格朗日方法建立了电动绳系离轨过程姿态动力学模型,描述了其在轨运行过程当中的面内外姿态变化情况,分析了电动绳系动力学模型实现面内外姿态运动解耦的条件,随后结合轨道动力学模型第十一代地磁场模型,在考虑重力梯度力矩和安培力矩作用的条件下,从理论上综合分析了电动绳系面内运动特性。本文最后建立了电动绳系离轨数值仿真模型,分别在考虑和不考虑面内摆角条件下,对电压变化、降轨高度和面内摆动等进行了对比分析,仿真结果说明,在考虑面内摆角的条件下,其离轨过程分析结果更为合理。