一种基于易损性分析的空间碎片撞击风险评估方法
周智炫,柳森,任磊生,马兆侠
(中国空气动力研究与发展中心超高速所,绵阳621000)
1 引言
随着人类空间活动的增加,空间碎片的数量不断增加,已对在轨航天器的安全构成了严重的威胁。国际空间站 (ISS)在设计之初,为了评估空间碎片对其撞击的风险程度,相关风险管理部门使用一种非击穿概率 (PNP)的指标来进行量化,目前已成为各国进行航天器撞击风险评估的标准之一。PNP通常以航天器结构或部件壳体的穿透与否作为失效判据,考虑的是航天器的结构损伤问题。但事实上,防护结构的击穿并不一定会引起部件功能的降阶,部件功能的降阶也不一定会引起整个航天器系统失效;此外,部件的损伤模式多种多样,每种损伤模式都有可能对航天器部件、分系统、系统造成不同类型和程度的影响。NASA、ESA以及俄罗斯等均已意识到这种问题,并开展了多项研究。NASA、ESA等先后对国际空间站的内部部件,如太阳能电池、蓄电池组、压力容器、电子盒、电缆束等,进行了易损性实验,给出了这些部件在空间碎片超高速撞击下失效的研究结果[1-6]。Schäfer,F.等人根据实验结果提出了考虑航天器结构失效和部件功能失效的弹道极限方程[7]。俄罗斯开发了计算机程序“BUFFER”,既可评估太阳电池阵、辐冷器、增强型防护构型等对ISS舱段压力舱壁起到的防护作用,也可针对空间碎片侵彻ISS的薄板部件产生二级碎片的随机碰撞进行建模,分析二级碎片碰撞的影响[8]。
因此,评估航天器在空间碎片撞击风险需要一种更为科学的方法和指标,能综合考虑航天器在空间碎片撞击下的结构失效和功能降阶问题,易损性分析方法就是其中之一。易损性分析方法从部件的结构失效和功能降阶出发,使用失效树或其他分析方法建立部件的故障与系统故障之间的联系,计算出系统故障的发生概率,并将其作为分析评估的指标。从理论上来说,易损性分析方法能比PNP更准确地描述航天器的撞击风险。一些学者已经开展了部分研究。例如,EMI的N.Welty等人提出了一种用于预测空间碎片撞击下卫星的系统级影响的易损性分析方法[9]。该方法结合M/OD(Meteoroid and Orbital Debris)环境模型、弹道极限方程、航天器暴露面积遮挡处理算法等计算航天器在空间碎片撞击下的结构损伤概率,利用失效树分析法 (FTA)分析航天器内部部件的功能失效程度,为航天器的失效概率分析提供了一种新思路。王彬、庞宝君等人也提出了一种评估航天器易损性的分析方法,针对航天器系统完全解体和非致命性失效 (功能降阶)两种失效模式,利用NASA解体模型和SRL弹道极限方程作为判断准则,运用损伤树分析法求解航天器的系统失效概率[10]。
本文以卫星为例提出了一种用于航天器撞击风险评估的易损性分析方法,该方法着重考虑二次碎片/碎片云粒子的撞击对航天器内部部件造成的结构失效和功能降阶,在对航天器部件的失效模式及影响分析 (FMEA)的基础上,利用射线跟踪法和失效树分析法计算航天器在空间碎片撞击下发生不同损伤等级的系统失效概率PK,并以此作为航天器撞击风险评估的指标。
2 航天器易损性分析方法
2.1 总体思路
航天器在空间碎片撞击下易损性分析方法的具体分析过程如下:
首先根据航天器任务参数和M/OD环境模型计算航天器单位暴露面积上的M/OD通量,结合航天器的几何结构采用射线跟踪法 (包含碎片云模型)计算部件的命中概率ph;根据部件的撞击特性计算航天器部件的命中失效概率pk/h;结合ph和pk/h计算部件的失效概率pk;与此同时,分析航天器在执行任务过程中遭受空间碎片撞击后可能发生的故障情况,定义航天器的损伤等级;开展航天器的FMEA分析,确定航天器部件的失效模式对航天器分系统、全系统的影响;最后,根据失效树分析结果和部件的失效概率Pk计算整个航天器在不同损伤等级下的系统失效概率Pk,如图1所示。

图1 航天器在空间碎片撞击下的易损性分析方法Fig.1 Vulnerability analysis method for spacecraft under impact by space debris
2.2 航天器的结构损伤计算
利用射线跟踪法和碎片云模型分析碎片/碎片云粒子在航天器内部的弹道轨迹,采用弹道极限方程和损伤方程计算航天器结构、部件壳体在空间碎片撞击下的损伤情况。
2.2.1 射线跟踪法
“射线跟踪法”是指用一条具有指定质量、速度、起点和方向的射线来模拟单个碎片运动轨迹及其侵彻行为的方法,如图2所示。本文利用射线跟踪法计算每一个碎片/碎片云粒子对航天器结构和部件壳体的损伤程度,确定其被撞击在哪个部位,以及是否被击穿。
当产生碎片云时,碎片云有可能同时损伤多个部件,因此判断碎片 (射线)是否撞击到航天器的结构或部件壳体是首要问题。弹目相交算法解决了碎片是否与目标结构/部件壳体交会,以及如何交会的问题。判断碎片可能撞击到哪些结构和部件壳体,实际上就是射线与航天器计算机模型结构和部件壳体的一次平面或二次曲面进行求交运算。如果相交,则说明射线击中目标结构或部件壳体。利用输入的目标结构、部件的几何数据,根据解析几何的坐标变换理论,对射线二次曲面进行求交运算,便可得到撞击点的坐标、撞击角度等信息。

图2 射线跟踪法示意图Fig.2 Schematic diagram of ray-tracing method
射线跟踪法需要考虑射线的产生/终止、偏转和分叉。其中,射线的产生/终止是指碎片穿靶后产生碎片/碎片云,或者碎片无法穿透靶板,由弹道极限方程来判断;射线的偏转是指碎片撞击靶板产生反溅,或斜撞击时发生跳弹、穿靶后碎片出射角度发生变化;射线的分叉是指碰撞过程中碎片云的产生,由碎片云模型决定。在运算过程中,碎片与目标的每次撞击都被当作是独立事件,每次事件都利用 “初始状态”计算路径。
为了描述空间碎片超高速撞击航天器结构后形成的碎片云细节,本文采用碎片云模型来确定碎片的速度、质量和空间角度分布。碎片云分布模型使用分布函数来描述碎片质量分布、碎片速率分布、碎片空间角度分布,结合Monte Carlo方法实现各种撞击条件下碎片云的随机生成,如图3 所示[11-13]。
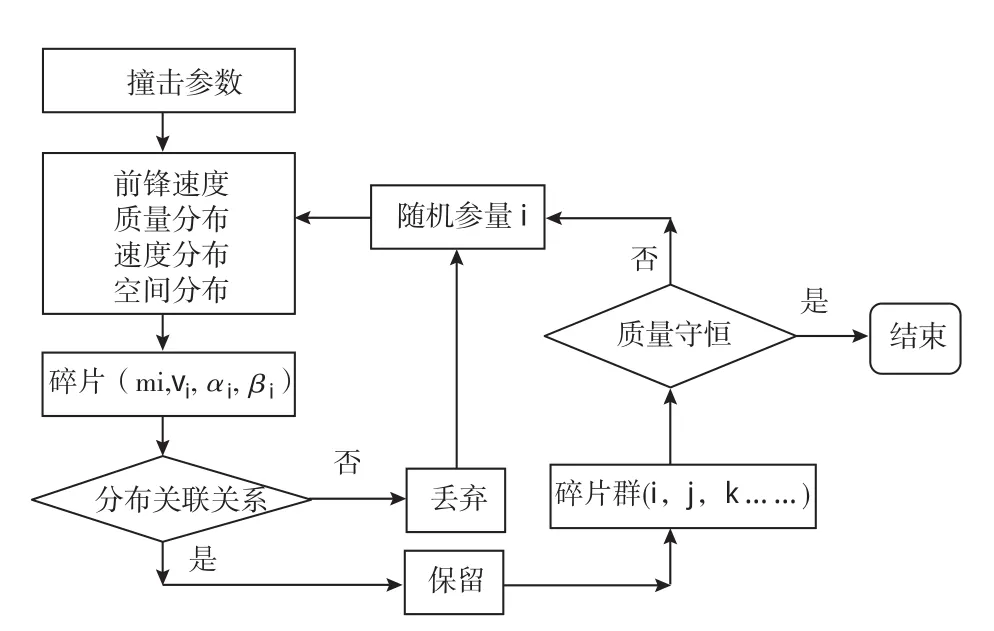
图3 碎片云模型计算流程图[11]Fig.3 Flow chart of debris cloud model computation
2.2.2 弹道极限方程和损伤方程
弹道极限方程用来判断航天器结构、部件壳体是否被空间碎片击穿,决定射线的产生和终止。根据靶板结构的不同采用的弹道极限方程也有所不同。例如,当目标为单层金属板结构时,可采用JSC弹道极限方程;当目标为蜂窝板结构时,可采用修正的Christiansen-Cour-Palais弹道极限方程。
损伤方程用来评估航天器结构、部件在空间碎片撞击下的损伤程度。例如,描述成坑尺寸的方程、描述穿孔大小的方程、描述玻璃裂纹尺寸和粉碎区尺寸的方程等等。还有一类损伤方程,也叫侵彻方程,通常用于描述高速/低速下碎片穿靶后 (未破碎)的弹道参数,如剩余速度、剩余质量和弹道偏转方向等,如THOR方程、BRL方程、Recht方程等。理想状态下,航天器结构、部件的各种损失模式与撞击参数之间都可以建立数学关系,形成不同的经验或半理论半经验的损伤方程。这些方程能有效给出航天器结构、部件在空间碎片撞击下的损伤情况,从而为后续的功能失效分析提供支持。
2.3 航天器部件的失效分析
根据航天器遭受空间碎片撞击后对遂行任务的影响程度划分航天器的损伤等级,结合部件的失效模式完成航天器的FMEA分析,计算航天器部件的失效概率Pk。
2.3.1 FMEA分析
FMEA用于分析航天器部件失效模式的每种可能形式对航天器预定任务的影响程度,为航天器的易损性评估提供准则和依据。
采用 “损伤等级”来表征空间碎片撞击对航天器预定任务的影响程度。例如,可将卫星的损伤等级划分为三个等级:“K”级、“A”级和“B”级。其中,“K”级表示卫星发生灾难性故障,任务立即失败;“A”级表示卫星发生严重故障,一段时间后失去控制,影响任务完成;“B”级表示卫星部分功能丧失,但未失去控制,任务降级。
FMEA的具体过程为:确认和提供航天器部件所有可能的失效模式,根据航天器部件/分系统的基本功能,确定航天器每种部件的失效模式对分系统和航天器任务的影响,以及航天器的损伤等级,形成FMEA表格。表1给出了某卫星的推进分系统在M/OD撞击下的FMEA分析结果。
2.3.2 部件的失效概率pk
航天器部件的失效概率pk是指航天器部件被碎片/碎片云粒子撞击后,失去部分或全部功能(功能降阶)的概率,亦即各种失效模式的发生概率。
假定碎片的每一次撞击都是独立事件,将航天器表面划分为j个单元,则部件在速度为vi的碎片撞击下的失效概率可由部件的命中概率和命中失效概率两部分组成:


表1 卫星推进分系统在M/OD撞击下的FMEA结果Tab.1 FMEA results of satellite subsystems under M/OD impact
当运用碎片云模型模拟航天器内部撞击碎片云的空间分布并形成射线时,需要对碎片云的特征(尺寸、速率、空间张角等)进行 “挑选”。每一项特征都采用Monte Carlo法进行随机 “挑选”,所有特征的乘积即为部件的命中概率:

式中,p(vi,j)(D)为碎片直径为D的概率,p(vi,j)(v)为碎片速率为v的概率,p(vi,j)(φ)为碎片经纬张角分别为θ、φ的概率[11]。
国际上通常采用弹道极限方程来判断航天器部件是否失效,这种判断标准工程应用便捷但是过于简单,仅用 “击穿”或 “非击穿”不能完整地描述部件的多种失效模式。例如,压力容器在遭受空间碎片撞击下可能发生爆裂、穿孔、成坑、裂纹等几种失效模式;此外某些部件,如电子盒,在外壳被穿孔后不一定会100%导致部件失效。由此提出从两个方面来描述航天器部件的命中失效概率pk/h:部件结构的损伤概率和部件功能的某种程度上的降阶概率。定义j单元内的部件在vi碎片撞击下的命中失效概率为部件结构的失效概率和功能失效概率的乘积:

2.4 航天器系统的失效分析
航天器系统的失效概率PK是指航天器被碎片撞击后发生某一损伤等级 (功能降阶程度)的概率,其表达式与部件的失效概率pk类似:
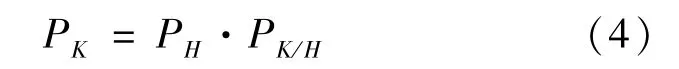
式中,PH为航天器外部结构被空间碎片撞击的概率,由NASA的ORDEM2000模型计算获得,PK/H为航天器的命中失效概率。
2.4.1 航天器系统的命中概率PH
根据ORDEM2000可知,航天器外部结构第j块单元格遭受速度为vi的碎片撞击的概率为:

式中,φvi为碎片通量,1/(m2·a1);Aj为航天器外部结构第j块单元格的暴露面积,m2;t为航天器在轨时间,年。
则航天器遭受所有碎片撞击的概率为:

2.4.2 航天器系统的命中失效概率PK/H
本文利用失效树法计算航天器全系统的命中失效概率PK/H。失效树的分析过程与FMEA类似,都是将部件的失效模式与航天器任务的影响程度(损伤等级)相联系。区别在于前者是自上而下,后者是自下而上。失效树根据逻辑门符号建立的树形图,求出最小割集,运用布尔运算和概率论方法计算顶事件出现故障的概率。
最小割集的故障概率等于它所包含的底事件概率的乘积:

式中,p(Cr)为第r个最小割集的故障概率;xl为第r个最小割集中第l个底事件;pxl为第r个最小割集中第l个底事件的发生概率。
假设各最小割集相互独立,在实际的工程问题中可以采用近似的独立事件 “和”的概率公式求解顶事件T发生的概率:

定义失效树的顶事件为航天器目标的某一损伤等级,中间事件为航天器分系统的损伤模式,底事件为航天器部件的失效模式 (根据FMEA分析结果提供)。当已知航天器部件的失效概率pk后,根据式 (5)、式 (7)、式 (8)可计算航天器第j个单元格内遭受vi碎片撞击发生某一损伤等级时的全系统命中失效概率:
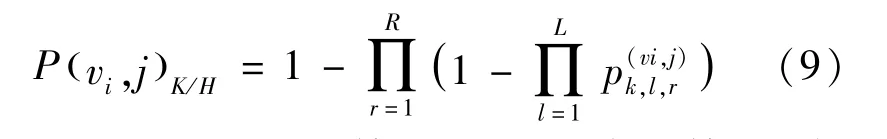
式中,p(vi,j)k,l,r为第r个最小割集中第l个部件的失效概率,由式 (1)~式 (3)计算获得。
则航天器遭受所有碎片撞击后的命中失效概率为:

3 算例
假设某模拟卫星主体结构为2.2m×2.2m×1.72m的立方体,轨道高度为400km,轨道倾角98°,偏心率0,发射年份2016年,在轨运行1年。采用ORDEM2000计算直径1cm的空间碎片的通量,结果如图4所示。
为减轻计算量,仅挑选偏航角为65°、速度为6.5km/s时的碎片通量进行计算,此时碎片通量为5.5512×10-8(m2·a)-1。假定电子盒的功能失效概率为0.8,天线和太阳能电池阵的功能失效概率为0.2,其他部件的定为1。结构和部件壳体的均根据弹道极限方程判断,当di≥dc时,为1,否则为0。建立的卫星发生A级损伤的失效树和卫星的PK分布云图分别如图5和图6所示。

图4 1.0cm空间碎片通量 (ORDEM2000)Fig.4 1.0cm space debris flux(ORDEM2000)

图5 卫星A级损伤失效树Fig.5 A-level damage failure tree of satellite

图6 卫星A级损伤的PK分布云图Fig.6 A-level damage PKdistribution cloud map of satellite
4 结论
本文提出了一种用于航天器的空间碎片撞击风险评估的易损性分析方法,该方法采用射线跟踪法模拟碎片/碎片云粒子在航天器内部的弹道轨迹,考虑了部件的结构失效和功能降阶问题,将部件的失效模式与航天器系统的功能降阶紧密联系起来,利用失效树方法计算航天器系统失效概率PK,并以此取代PNP作为航天器的空间碎片撞击风险的评价指标,可预测航天器在遭受厘米/毫米级空间碎片撞击后的系统失效影响。
但是,该易损性方法也存在一些缺陷:一是失效树的建树过程依赖于对部件各种失效模式以及部件功能的降阶对航天器系统的影响等方面的详尽了解,实际上,目前我们对航天器上各种部件的撞击特性和失效模式还远谈不上掌握,例如撞击冲击波、振动以及瞬时电压或脉冲等效应的影响尚在研究之中;二是失效树方法采用最小割集算法对其结构函数进行简化计算,当所建的失效树较为复杂时,精确解算法可能出现 “组合爆炸”的现象,导致计算无法进行下去,而采用近似算法则会引起计算精度大幅度下降;三是PK的计算基于部件的命中失效概率PK/H,虽然在本文中提出了一种计算方法,但实际上到目前为止还没有一个通用的方法能得到准确的PK/H、PK/H最终是在试验、数值仿真、航天器在轨故障统计和工程判断获得,这也为系统失效概率的计算带来了不利影响。

