提高复杂拓扑风电场动态等值水平的增广路径标号算法
石军,吴建辉,管保安,王递进
(1. 国网河南省电力公司商丘供电公司,河南 商丘 476000; 2. 武汉泰可电气股份有限公司,武汉 430070)
0 引 言
为响应低碳、环保、绿色的能源可持续发展战略,风力发电技术越来越成熟,随着风电装机容量不断增大,拓扑结构日益复杂,系统稳定性受到风电场模型的影响越来越大[1-2]。风电场包含机组众多,风机模型阶数高,非线性特性严重,因此建立风电场详细模型进行分析会导致稳定计算不收敛问题,故在风电场控制及仿真分析时,需要将风电场复杂结构简化为单机或多机模型,将各运行参数进行等值计算[3-5]。调查表明,贵州某大型风电场装机容量可高达297 MW,考虑到机组选址的限制[6],上百台风电机组的布局并不规则,造成风电场拓扑结构复杂多变。风电场内一般采用电缆线路将风机汇集至并网点,数量众多、结构复杂的线路造成的功率损耗与风电场经济效益密切相关,同时,研究表明电缆线路参数会影响风电场等值模型的动态特性输出[7-8],目前对于风电场建模仿真一般不涉及集电参数等值。因此,基于集电参数功率损耗的风电场等值建模不仅需要考虑大型风电场网络拓扑的复杂性,而且还需兼顾风电场并网点输出特性的一致性。
目前,对于风电场的等值建模研究已有较多报道。文献[9]提出多机动态等值方法,并考虑到风电场风速差异对功率动态特性的影响。文献[10]提出双馈风机的三机表征动态等值建模,按照电压加权平均等值方式进行电缆线路等值。文献[11]提出进行风电场电磁暂态仿真分析时,考虑风速变化时,电缆线路参数对动态特性的影响显著。从文献中看出,目前对于风电场等值模型研究主要包括机组动态特性的等值建模方法,以及基于动态表征的机组分群方法,而对电缆线路等值的研究并没有涉及风电场机组布局的复杂性,对风电场功率损耗也很少考虑。
以双馈风机风电场为例,针对大规模复杂拓扑风电场动态等值建模问题进行深入研究。首先,建立BPA风电场仿真模型以及两机电网模型。然后提出采用增广路径标号算法分组识别大型风电场复杂拓扑结构特性,经过干线式和放射式接线组合的多次迭代后,完成复杂拓扑风电场的单机等值建模。最后,采用BPA程序进行两机系统的仿真分析,通过典型49.5 MW风电场验证了所提出的等值方法能够解决复杂拓扑风电场等值问题,提高了动态等值水平;通过不同规模风电场的动态等值水平,比较并网点功率及频率特性,说明风电场精细化建模对于大规模风电场适应性不足,仍须进行多机等值建模。
1 风电场等值建模
双馈风力发电系统的控制框图,主要包括三个部分:转子侧变流器控制、定子侧变流器控制及风力机[12]。控制对象为双馈电机的机械转矩输入和背靠背变流器的控制信号,控制策略为最大风速跟踪控制[13-14]。
1.1 风电机组模型
dq轴的电压和磁链方程可以写出双馈电机在dq坐标系统的电磁暂态数学模型:
(1)
双馈风电机组静态模型包含定子侧电阻电抗rs、Ls,转子侧电阻电抗rr、Lr,励磁电抗Lm,以及系数ρ。由式(1)可知,对于同调机组而言,参数之间呈线性关系,因此可采用倍数等值计算方法,即:
(2)
风力机机械部分包括慢速轴和快速轴两部分,通常选择两质量块模型来描述。
n台风机的动态参数等值计算公式如下:
(3)
式中Tg为发电机转动惯量;Ks为轴系刚性系数;Tt为风轮机及叶片转动惯量,含有下标(n)的量为等值后的机组参数。
1.2 风电场拓扑结构
随着风电场规模进一步扩大,由于风机分布不均,距离并网点较远,需多段电缆线路连接各风机至并网点,风电场内功率损耗主要为电缆线路损耗以及变压器损耗[15]。风机输出功率在传输至并网点的过程中,每经过一台风机,输出功率的汇集后,集电线路产生的功率损耗逐渐增加[16-17]。
文中基于功率损耗一致原则对风电场集电网络进行等值,等值模型与原模型能够保持功率损耗量一致和并网点电压基本一致。
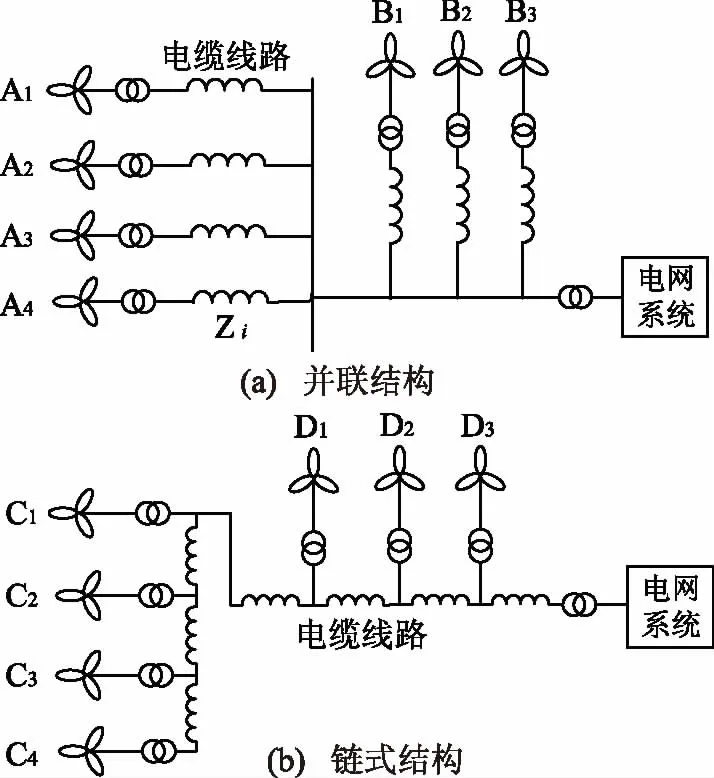
图1 风电场基本拓扑结构
图1所示为风电场的两种基本拓扑结构,图1(a)表示A组和B组风机的经升压变压器后有各自的电缆线路段,线路末端汇集至电网系统并网点,即并联结构;图1(b)表示C组和D组风机不具有各自的电缆线路段,风机经升压变压器后以电缆线路相互连接,最后所有机组功率经电缆线路接入并网点,即链式结构。
并联结构拓扑中电缆线路和升压变压器经过的功率和电流量只与各自的风机运行状态相关,而在链式结构中,必须考虑每段电缆线路中流过的功率流。
因此,依据功率损耗一致原则进行风电场电缆线路参数的等值计算。其中,具有n台风机的并联结构风电场的等值电缆线路参数计算如下:
(4)
链式结构风电场的等值电缆线路参数采用递推法。
图2所示为链式结构的等值计算过程,结合式(5)的计算公式,将蓝色D1和D2机组等值为红色标记的单机模型,然后将红色D3等值为黑色标记的单机模型。从而逐步将链式结构风电机组等值为单机模型。
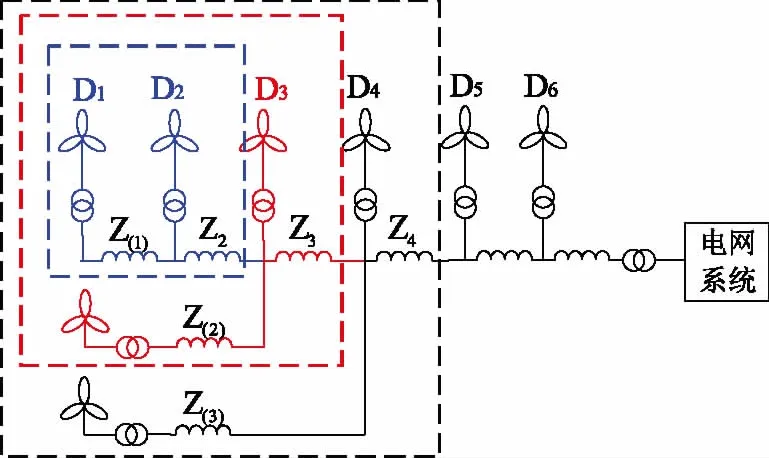
图2 链式结构等值过程
式(5)的推导依据总功率损耗一致原则。
(5)
式中下标(n)、(n+1)表示n、n+1台风机等值后的电缆线路阻抗,n+1表示第n台机相接的电缆线路阻抗。
2 增广路径标号算法
图论中计算最大流问题常常采用增广路径,标号算法将复杂抽象图形简单化,有利于拓扑结果的划分[18-19]。结合增广路径和标号算法,提出增广路径标号算法,以解决风电场网络结构划分问题,包括以下四步:(1)计算当前网络最大流,识别当前网络的链式节点组;(2)依据式(5),将链式节点机组间电缆线路进行等值;(3)更新等值后网络结构,计算并识别当前网络的并联式节点组;(4)依据式(4),将并联式节点组间电缆线路进行等值。更新网络参数后进行多次迭代,直至网络最简。
风电场网络拓扑为无环、无重边的简单图,记为G=(V,E),其中V代表节点集,E代表支路集,节点为风电机组及升压变压器模型的简化表示,节点参数表示所代表风机相关参数。设节点数为n,节点为ui,节点功率矩阵P为各节点注入功率,即该节点所接风电机组输出功率,Zij为连接节点ui、uj的支路阻抗值,(ui,uj)∈E表示两节点在网络拓扑中能构成支路;反之,表示节点不相连,不能构成支路。邻接矩阵A=(aij)n×n为各节点间阻抗值构成的矩阵。
第一步,筛选网络中端节点的集合,即除并网点以外,有且仅有一条支路相接的节点;
第二步,寻找链式有序节点组Utrunk,该节点组中相邻节点按照顺序依次经过电缆线路首尾相接组成链式接线形式。由于Utrunk中一定存在一个端节点,因此以端节点为节点组中第一个元素,按照连接顺序依次标号,直至节点的相接节点数大于2;
第三步,由每组有序节点组Utrunk(ui),求得对应节点的节点功率矩阵Ptrunk。依据式(5)计算该链式接线机组的等值电缆线路阻抗Zeq1,并进行风电机组参数等值,机组功率等值为Peq1;
第四步,更新节点功率矩阵P及邻接矩阵A:删除P、A中有序节点组Utrunk(ui)对应的节点元素,将每组中所有节点用的等值节点、阻抗和功率表示,形成新的邻接矩阵。若维度div(A)>2,则由A更新端节点集Up0,转第五步;若div(A)=2,则运算终止;
第五步,遍历所有端节点的相接节点,将具有共同相接点的端节点划分为一组,定义并联式节点组Uradial,表示经电缆线路后功率输出点接于同一相接节点的并联式节点组信息;
第六步,将并联式节点组的对应节点功率矩阵表示为Pradial,由所有Uradial及相应的Pradial数据,依据式(4)计算该并联式接线机组的等值电缆线路阻抗Zeq2,并进行风电机组参数等值,机组功率等值为Peq2;
第七步,再次更新节点功率矩阵P及邻接矩阵A:删除矩阵A、P中并联式节点组Uradial对应的节点元素,将每组中所有节点用的等值节点、阻抗和功率表示,形成新的邻接矩阵。若维度div(A)>2,转第一步;若div(A)=2,则运算终止。
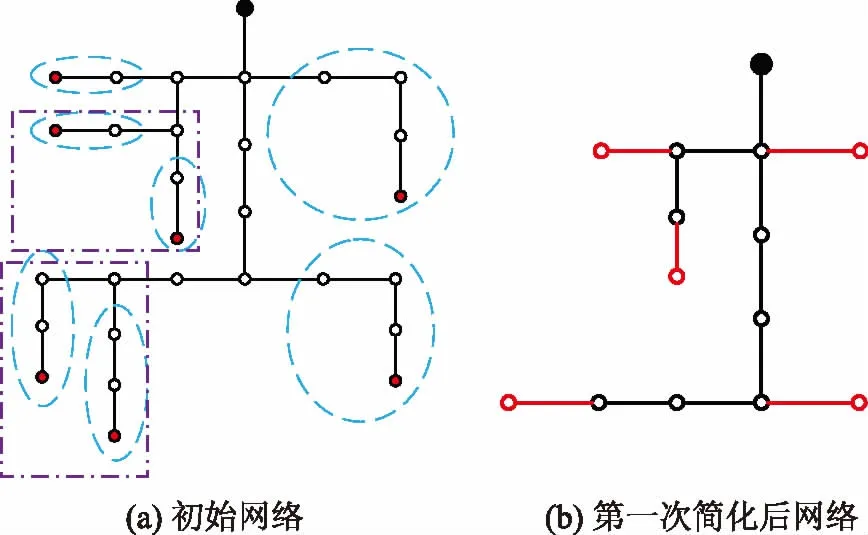
图3 网络结构划分示意图
图3(a)中红色节点为端节点,蓝色虚线区域节点为以链式接线的节点组Utrunk,紫色区域节点为以并联式接线的节点组Uradial。图3(b)是经上述七步的模型识别及等值后的第一次简化网络,红色线路和节点为图3(a)中相应区域等值模型。经过多次网络的循环化简,最终建立单机等值模型。
3 BPA两机电网模型仿真
将风电场等值建模应用在两机系统中,如图4所示为风电场等值后系统图。考虑风速、风向以及尾流效应的影响,场内机组运行状态不一,因此,首先建立33台机组的典型风电场模型,比较不同运行状态、不同等值模型的动态仿真差异,以验证文中增广路径标号算法的适应性。
建立两种等值模型,其中,等值模型A为按照文中等值方法建立的等值模型;等值模型B为集电参数累计相加后的常规等值模型。
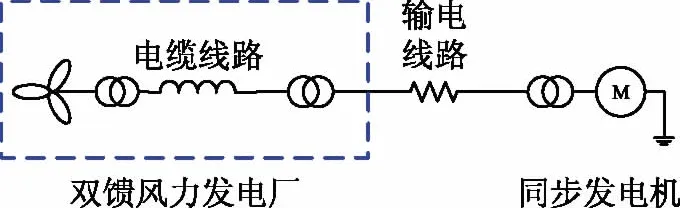
图4 两机仿真系统示意图
然后分别建立10机、50机、90机、130机构成的风电场模型,在两机系统中比较不同规模风电场等值模型的动态响应特性。
3.1 典型风电场验证
33机典型风电场总输出功率为49.5 MW,拓扑结构为15台机链式组和18台机链式组并联汇集,等值参数见表1。

表1 等值模型参数
设置两类风电场的运行状态,如下:(1)所有风电机组输出功率相同;(2)保持风电场总输出功率为60%,线路末端机组输出功率最高,各机组输出功率按线路连接顺序依次递减,间隔0.08 MW在尾流效应对功率影响的范围内。
并网点前侧发生三相短路故障,0.1 s后切除故障,以风电场并网点有功功率响应作为等值模型的评价指标,图5为并网点有功功率仿真结果。
图5 故障下风电场有功功率动态响应
由线路有功功率动态响应曲线可知,在故障恢复阶段,等值模型A、B与详细模型存在一定差异,等值模型A与详细模型差异较小,动态适应性较强。
3.2 不同规模风电场仿真
比较等值模型A和B的等值方式,结合第二节内容可知,链式结构对电缆线路参数等值的影响最大。为了验证文中等值方法对不同规模电网的适应性,将风电场拓扑结构统一设置为几组链式组并联汇集的形式,如表2所示。

表2 风电场拓扑结构
仿真分析并网点前侧发生三相短路故障,0.1 s后切除故障,在风机出力均为83%的运行状态下,比较等值模型与详细模型差异,如图6、图7所示。
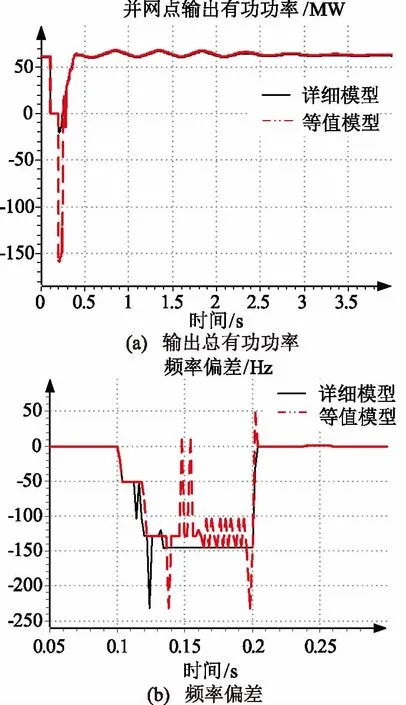
图6 50台机风电场仿真
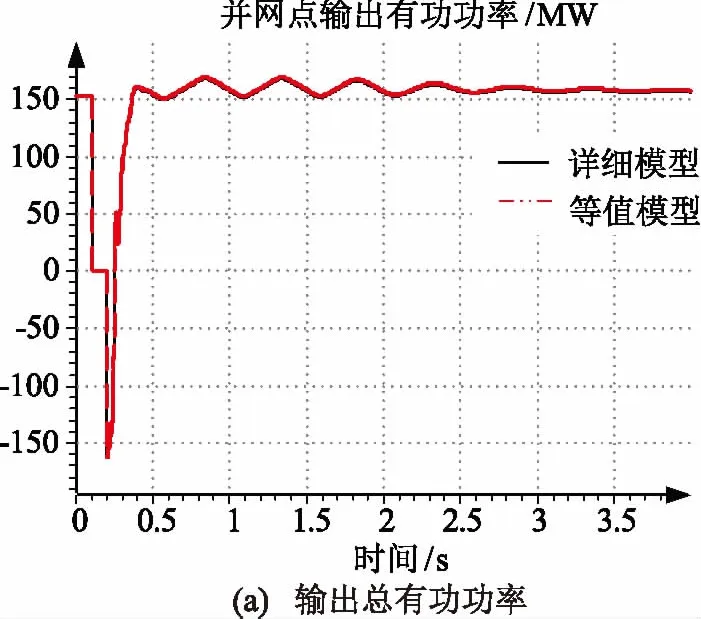
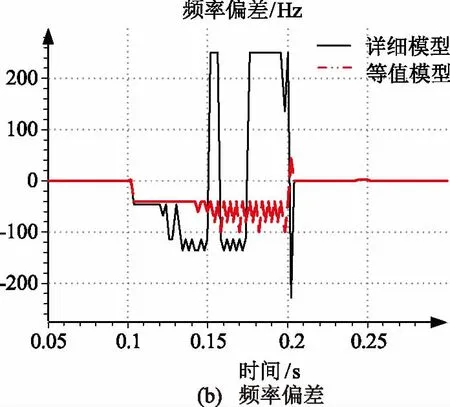
图7 130台机风电场仿真
以50台机以下的风电场表示小规模风电场,其响应特性与图6相似,以130台机以上的风电场表示大规模风电场,其响应特性与图7相似。
由并网点输出有功功率曲线可知,三相短路故障后总输出功率立即减为零,在0.1 s后故障恢复时总输出功率反方向吸收0.1 s左右后,逐渐恢复至初始功率值。比较图6(a)和图7(a),在故障恢复瞬间,小规模风电场的等值模型暂态响应特性适应性不足,功率反向吸收值明显高于详细模型;而大规模风电场的等值模型暂态响应特性与详细模型基本保持一致。
由系统频率偏差曲线可知,在故障发生后的0.1 s内,并网点频率发生较大波动,等值模型与详细模型曲线的变化趋势大体相同。比较图6(b)和图7(b),大规模风电场等值模型的频率波动较小(最低 -100 Hz,最高40 Hz),与详细模型相差较大(最低 -220 Hz,最高240 Hz),因此,适应性不足;而对于小规模风电场等值模型与详细模型相比,频率偏差范围相同,波动次数较多。
对于大规模风电场,总输出功率较大,电缆线路功率损耗相对量较小,对总有功功率的影响越来越小。因此,精细化的风电场等值建模对并网点功率适应性提高,但对频率暂态响应的影响较大,可适当增加等值机组台数。
4 结束语
针对大规模复杂拓扑风电场动态等值建模问题进行两方面的研究:建立BPA风电场仿真模型以及两机电网模型;提出采用增广路径标号算法分组识别大型风电场复杂拓扑结构特性,完成复杂拓扑风电场的单机等值建模。最后,采用 BPA程序进行两机系统的仿真分析,结论如下:
(1)以典型49.5 MW风电场为例,分析对比详细模型和两种等值模型的并网点输出功率暂态特性,验证了所提出的等值方法能够解决复杂拓扑风电场等值问题,提高了动态等值水平,比常规等值模型更精确,适应性高;
(2)分析不同规模风电场的动态等值水平,比较并网点功率及频率特性,结果表明所提出的风电场精细化建模对并网点功率适应性提高,但对于大规模风电场适应性不足,仍须进行多机等值建模。

