基于优先级排序的聚类风电机组爬坡有限度控制策略研究*

王致杰，孙丛丛，江秀臣，刘三明，王东伟，盛戈皞

(1. 上海电机学院 电气学院，上海 201306； 2. 上海交通大学 电气工程系，上海 200240)

0 引 言

风电爬坡事件会给电网带来严重的冲击，尤其是下爬坡事件发生时，供给侧对风电进行大面积的切机保护处理，造成电网供电能力不足，从而导致系统电压不稳，频率下降，电能质量低于国家标准，严重情况下，电网必须切负荷处理，给电网用户带来极大的经济损失。因此，如何对风电爬坡事件进行有效控制，以提高风电出力的可控性和稳定性，降低风电爬坡对电网的影响，具有重要的研究意义。

由于风电爬坡事件对电网具有较大的影响，目前国内外学者主要从电网系统的调频调峰、调压以及功率平滑等方面对风机进行了研究，并给出了相应的控制策略。文献[1]介绍了备用功率控制(PRC)策略和改变发电机转子转速的控制策略，达到电网调频的目的。文献[2]也是通过增加频率控制策略改变双馈风力发电机的控制方式，从而改变风机的有功出力，进一步改变系统的频率，实现频率控制调节系统频率的目的。文献[1-2]是通过各类方式调节风机进而调频调峰，其控制方式的时间较短，但是风电爬坡也有其一定的独特性，即风电爬坡的时间一般较长，采用上述的控制方式，其达到的风电爬坡控制效果相对有限。文献[3]在模糊控制的基础上，建立了变桨距控制和发电机转矩控制模型，给出了相应的控制理论，该策略从低速到高速范围内，通过协调桨距与转速之间的控制策略，使其输出更加平滑的有功出力，但并未给出变桨距和变速协调的详细控制方法。文献[4]综合采用变桨距控制和超速法相结合的控制策略实现风电机组长时间的有功减载功能，其中变桨距控制实现变风轮的桨距角调节风机的出力功率的功能;而超速法实现控制转子转速实现调整风电机组有功出力的目标，两者相互协调配合作用，从而实现系统的调频需要。文献[5-8]为了增加电力系统运行的可靠性，介绍了变速控制和变桨距控制的协调方法，它们相互协调配合，共同改善电力系统的频率特性。文献[9-12]为了保持风电出力的平稳性，在风速变化时，通过快速改善了风机的出力特性，维持其出力的平稳变化。文献[13-15]为了提高电网系统的电压稳定性，通过改变风机的无功功率输出特性，协调有功输出功率。

基于上述考虑，文中建立了基于优先级排序的聚类风电机组爬坡有限度控制策略。首先，针对风电爬坡事件整个过程，将爬坡过程分为爬坡前的预防控制、爬坡中控制和爬坡后的恢复控制3个阶段，建立有限度控制模型。其次，针对爬坡过程中众多风电机组出力波动过程的多样性特点，综合采用相似性度量方法和模糊C均值算法聚类方法对风电机组进行聚类分析，将风电机组分类；再次，针对不同类别的风电机组和风电机组有限的控制能力，提出了基于优先级排序的各类风电机组的有限度控制策略，以提高风电场输出功率的稳定性和可控性。最后通过算例仿真验证文中控制策略的有效性。

1 风电爬坡过程分段

由于对风电场或场群的功率控制是在有限的程度上进行的，因此风电功率爬坡控制也称为有限度控制策略[16]，风电爬坡有限度控制策略如图1所示。

由于整个风电爬坡过程是一个长时间段，且在不同的时间段具有不同的特性，因此首先对爬坡过程进行分段处理。在有限度控制策略中，将整个爬坡过程分为3个阶段：第一阶段为预防控制阶段，即t0～t1时间段，其作用是为防止风电功率突变对电网的影响，即风电功率的强波动性及不确定性会对电网运行造成一定危害，提前增加风电输出功率，使风电输出功率缓慢增加，从而降低爬坡率，增加风电机组的可控性和稳定性；第二阶段为爬坡控制阶段，即t1～t2时间段，其作用是针对各类风机有限的控制能力，协调各类风电机组工作，实现最优控制策略，从而有效地跟踪目标出力计划；第三阶段为恢复控制阶段，即t2～t3时间段，其作用是减轻各类风电机组的负载，使其达到额定的最佳工作状态或达到额定的目标出力计划。风电爬坡分段过程如图2所示。

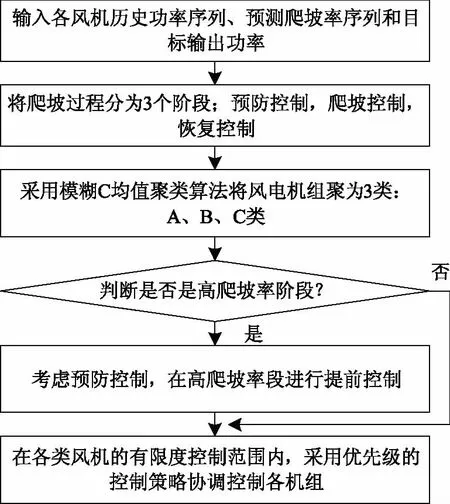
图1 风电爬坡有限度控制模型

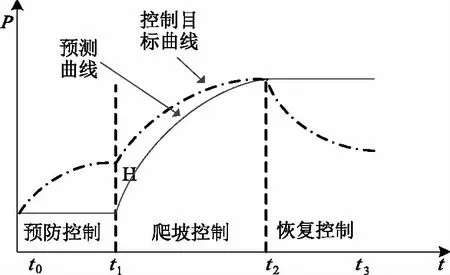
图2 风电爬坡过程分段图

采用预防控制可以降低爬坡率，因此需要提前判断高爬坡率和低爬坡率阶段，从而进行预防控制，低爬坡率和高爬坡率的定义如下：

(1)低爬坡率时间段：

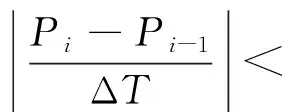
(1)

式中Pi为i时刻的风电功率值；ΔT为两个时间段的间隔；λL为爬坡率的阈值，该参数主要体现爬坡率相对大小的分界，由目标控制要求和风电场具体特性设置数值；

(2)高爬坡率时间段：

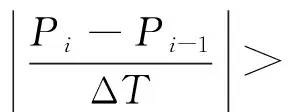
(2)

对于高爬坡率段，根据图1的有限度控制模型理论，应考虑预防控制，以达到降低爬坡率，实现风电场稳定运行的效果。

2 风电机组的相似性分析与聚类

针对风电机组出力波动过程具有多样性的特点，文中基于风电场历史功率数据，采用时间序列的相似性度量的数据挖掘方法找出数据间的相似性，然后采用模糊C均值算法对风电机组进行聚类分析，以降低风电机组类别，提高计算速度。

2.1 基于时间序列的相似性度量算法

该方法能够充分考虑功率序列幅度、偏移、噪声等问题，应用基于规范变换的方法来求取功率序列的相似判定矩阵，很好地处理了由于其欧式距离太大而不满足聚类条件的问题。其基本思想是：设窗口宽度为n，将要分析的原始序列分成m段，则原始序列变为x={p1,p2,...,pm}，用式(3)进行序列的偏移变化和幅度缩放[17]。

(3)

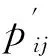
2.2 模糊C均值算法

模糊C均值聚类算法(FCM)是先取出n个向量，将其分为c个模糊组，再求各个模糊组的聚类中心，使其满足非相似性指标的价值函数为最小的条件[18]。

模糊C均值算法的输入数据集的隶属度之和总等于1。

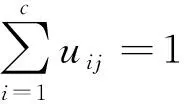
(4)

那么，模糊C均值(FCM)的目标函数就是：

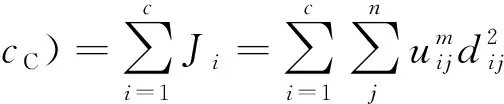
(5)

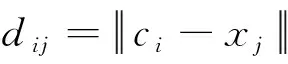
若对一个矩阵序列来说，则模糊C均值构造如下，新的目标函数为：

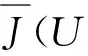
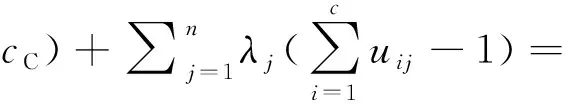
(6)

式中λj是式(4)约束条件的拉格朗日乘子。

对所有输入参量求导，使式(6)达到最小的必要条件为：

(7)

(8)

2.3 风电机组的聚类分析

首先采用时间序列的相似性度量方法将输入的风电机组历史功率数据序列根据式(3)进行变换，然后设定标准差阈值判定变换后的两功率序列是否相似，若相似，则相似判定矩阵中对应位置记为1，若不相似，则相似判定矩阵对应位置记为0，若输入的为k个历史功率序列，则由此得到一个k×k的相似判定矩阵，此为模糊C均值的数据预处理方法；通过相似判定矩阵的计算，得到的变换后的数据集，作为模糊C均值的输入数据，然后在模糊C均值算法中，设定合适的聚类类别数可以得到各个样本到类内中心的聚类，设定合适的隶属度阈值，便得到所需要的聚类结果。聚类过程如图3所示。

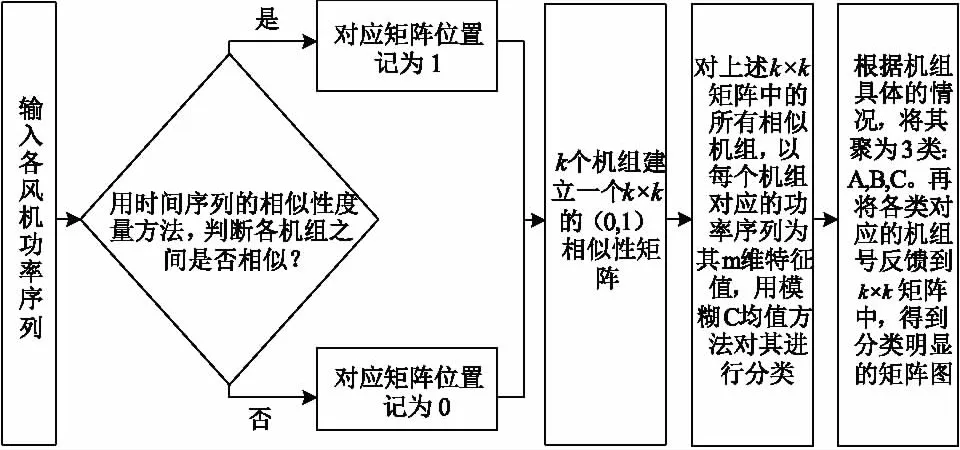
图3 风电机组的聚类模型

为了方便描述上述的各类风电机组的控制策略，现将聚类结果命名为A、B和C类共3类风电机组。A类风电机组表示完全可控的风机，即历史数据中，此类风电机组性能较好，未出现过故障；B类风电机组表示性能良好的半可控的风机，即历史数据中，长时间能够正常工作，性能良好，偶尔出现过故障的风电机组；C类风电机组表示性能一般的半可控风机，即历史数据中，短时间内能够正常工作，当外界环境变化时，容易出现故障的风电机组；若风电场中含有时常出现故障的风电机组，属于不可控机组，不在此聚类控制的考虑范围内，在采用算法聚类之前，统一规划到D类机组，D类风机不参与风电爬坡的控制。

3 基于优先级排序的风电爬坡控制策略的实现方法

针对不同类别风电机组不同的有限度控制能力，采用优先级的控制顺序，制定相应的控制策略。

ΔP=Porder-Pcur

(9)

式中Pcur表示风电场的当前出力值；Porder表示电力系统下发的功率指令值；ΔP表示整个风电场所需要的功率调整量。

对于爬坡过程，为了提高风电场的可控性，考虑不同机组状态风机的控制性能，优先调整可控性较强的风电机组，从而获得较好的控制效果。

(1)当ΔP>0时，即在输出功率增加的时候，不同类别风电机组控制的优先级顺序依次为：A类、B类、C类。

各类风机的可调容量为：

ΔPx=PXm-PXc

(10)

式中ΔPx为X类风电机组能够调整的容量，X为A,B,C；PXm为X类风电机组的最大输出功率；PXc为X类风电机组的当前输出功率。因此，风电场中所有风电机组的可调整的总容量为：

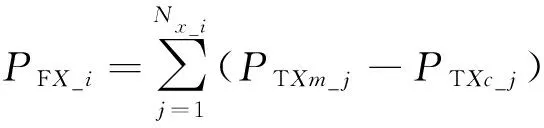
(11)

式中ΔPFX_i为i号风电场X类风电机组能够调整的容量；PTXm_j为编号为j的X类风电机组最大的输出功率；PTXc_j为编号为j的X类风电机组的当前输出功率；Nx_i为i号风场X类风电机组的数量。

为了提高风场的控制力，此处给出了可控系数αi，其值由不同风电机组在风电场中所占的比例决定，所占比例越高，则该值越大，所有的可控系数满足：

(12)

式中N为风电场的总数目。

(a)当0<ΔP<ΔPA时，先调整A类风电机组，则i号风场A类风电机组的总调整量为：

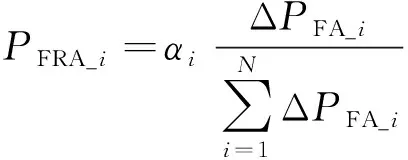
(13)

(b)当0<ΔPA<ΔP<ΔPA+ΔPB时，A类风电机组输出最大功率，B类风电机组进行输出功率增加的调整，i号风场B类风电机组的总调整量为：

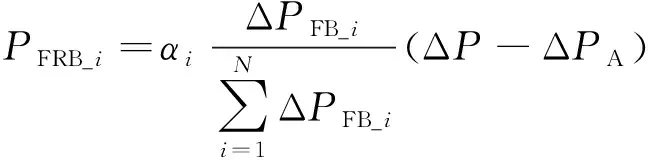
(14)

(c)当0<ΔPA+ΔPB<ΔP<ΔPA+ΔPB+ΔPC时， A类和B类风机都进行最大出力调整，C类风机进行的总调整量为：

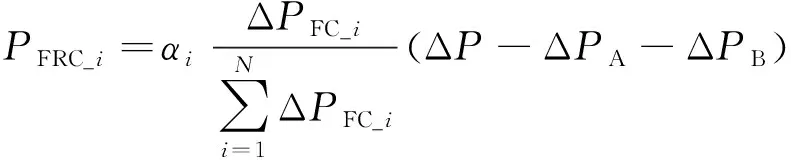
(15)

(d)当0<ΔPA+ΔPB+ΔPC<ΔP时，A类、B类和C类风机都进行最大出力调整；在输出功率增加的阶段，风电场中的各类风电机组的调整方案如下：输出功率需要增加调整的风电机组，其输出功率的调整量为ΔPTRX_i，X为风电机组的类别,则i号风电场中X类风电机组的单台调整量为ΔPTRX_i：

(16)

由于各类风电机组的调控能力有限，为了提高控制精度，规定了单台风电机组的最小调节限值Plim。若ΔPTRX_i大于ΔPlim，则将ΔPTRX_i直接下发给对应的风机；若ΔPTRX_i小于ΔPlim，则将其直接下发给NRX_i台风机，NRX_i由式(17)确定:

(17)

(2) 当ΔP<0时，即为输出功率降低(降出力)的情况，此时不同风电机组控制顺序的优先级依次为：C类、B类、A类。

各类风电机组的可调整容量为：

ΔPX=PXc

(18)

式中ΔPX为X类风电机组输出功率能够调整的容量，X为C,B,A；PXc为X类风电机组当前的出力；

为了提高风电场的可控性，给出了可控系数βi，其值由不同风电机组在风电场中所占的比例决定，所占比例越高，则该值越大，所有的可控系数满足：

(19)

式中N为风场的总数目。

(a)当ΔP<ΔPC时，C类风电机组作输出功率降低的调整，i号风场C类风电机组的输出功率调整量为：

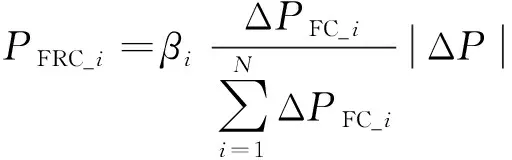
(20)

(b)当ΔPC<ΔP<ΔPC+ΔPB时，C类风机作切机动作，将输出功率降为零，B类风电机组作输出功率降低调整，i号风场B类风电机组的调整量为:

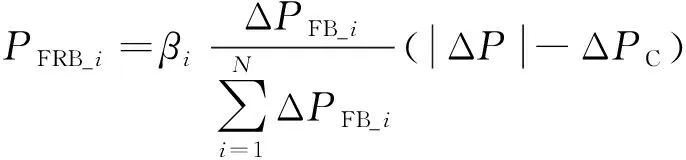
(21)

(c)当ΔPC+ΔPB<ΔP<ΔPC+ΔPB+ΔPA时，C类和B类风电机组进行切机处理，即B类和C类风电机组的输出功率降到零，A类风电机组作输出功率降低调整。

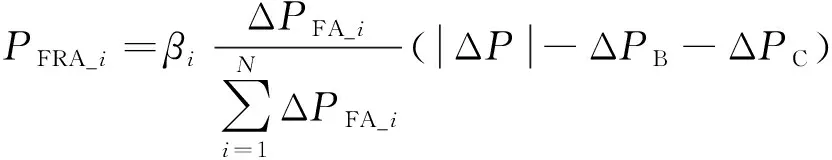
(22)

(d)当ΔP>ΔPC+ΔPB+ΔPA时，C类，B类和A类风电机组都切机，即功率都降为零。在降出力阶段，风电场中的各类风电机组的调整方案如下：需要进行输出功率降低调整的风电机组，其输出功率的调整量为ΔPTRX_i，X为风电机组的类别，则i号风场中X类风电机组的单台功率调整量为ΔPTRX_i：

(23)

若ΔPTRX_i小于-ΔPlim，则将ΔPTRX_i下发给相应的风机；若ΔPTRX_i大于ΔPlim，则下发给NRX_i台风机，NRX_i由式(24)确定:

(24)

4 算例分析

4.1 数据来源

算例数据来源于上海某风场2015年5月份到7月份的风场监测数据，其数据中含有28台风机这3个月的各项监测数据，数据中包含各风机的风速，功率，温度等值。文中采用此风电场中28台风电机组的数据进行仿真验证。

4.2 结果分析

(1) 风电机组聚类过程。

在风电机组聚类过程中，首先采用时间序列的相似性度量方法对风电功率的历史数据进行预处理。如图5所示：图中给出了两台风机的部分功率序列。红色的实线表示风机1的功率序列，蓝色的点横线表示风机2的功率序列。

图4 功率序列相似图

采用时间序列相似性度量算法，运用公式(3)将图4变换成图5所示。

图5 规范变换后的功率相似图

依照相似性度量方法，在数据预处理检测处理，发现有3台风电机组的历史功率数据出现大量的负数和零，因此判定这3台风电机组经常出现故障，属于坏的风机，剔除。将其余25台风机功率序列依照相似性度量算法，经规范变换后的两功率序列进行误差计算，设定阈值为0.5，确定相似判定矩阵，通过程序循环计算得到 的相似判定矩阵如图6所示，其中，1表示两个风电机组输出功率相似，0表示两个风电机组输出功率不相似。

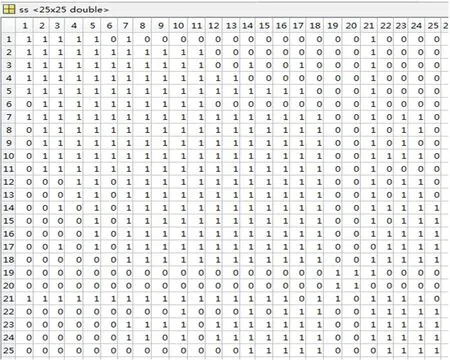
图6 风电机组功率序列的相似矩阵

为了直观反映这个风电场群中这25台正常工作的风机相似矩阵中的关系，将图6的矩阵表转化成如图7所示的矩阵图，黑色部分代表1，白色部分代表0。

图7 风电场功率相似矩阵图

通过时间序列的相似性度量方法进行数据预处理之后，将式(1)变换之后的数据集作为模糊C均值的输入，进行风电机组的聚类，在模糊C均值算法中，设置各参数如下：类别设置为3；隶属度矩阵指数设置为2；最大迭代次数设置50；迭代终止条件为：1e-5。经程序运算后，得到风电机组的聚类表如表1所示。

表1 风电机组聚类表

由表1可知，将风电机组分成了A、B、C三类，其中A类包含了11个风电机组；B类包含了5个风电机组；C类包含了9个风电机组。其原始数据中，已知的3台故障风电机组不参与控制策略，将其删除，因此暂未对其聚类。为了更直观的体现各风电机组之间的聚类情况，将表1中的聚类结果绘制成聚类矩阵图，如图8所示。

图8 风电机组聚类矩阵图

在此聚类图中，棕色的区域表示A类风电机组，黄色的区域表示B类风电机组，浅蓝色的区域表示C类风电机组，其余蓝色的区域表示两机组间不存在相互聚类关系。

风电场中各类风机聚类功率曲线如图9所示，实线表示A类风电机组，调节性能较好；点横线表示B类风电机组，调节性能一般；点线表示C类风电机组，调节性能相对较弱。

图9 风电机组聚类功率图

(2)风电爬坡的有限度控制策略分析。

在上述风电机组聚类的基础上，针对各类风电机组的波动性特点，在风电爬坡过程的3个阶段，考虑高爬坡率对风电质量的影响，采取预防控制方法，应用上述的数学控制方法对各类风电机组进行有限度控制，协调各类风电机组有效运行，提高风电场输出功率的稳定性和可控性。

根据仿真算例的历史数据，预测一段时间的爬坡率如图10所示。

在图10中，将所预测的爬坡率分为AB，BC，CD，DE，EF，FG共6段，其中AB，CD，EF这3段明显属于爬坡率较高的三段，根据文中的有限度控制模型理论，此3段属于高爬坡率段，应考虑预防控制进行调控，以达到降低爬坡率，实现风电场稳定运行的效果。对风电爬坡过程考虑提前预防控制方法，同时采用文中的数学量化方法对A、B、C这3类风电机组实行基于优先级排序的控制策略，各类风电机组协调运行，维持风电场的稳定性和可控性。高爬坡率时间段对应的有限度控制策略如图11所示。

图11 爬坡控制过程

从图11中可以看出，点横线的为原来的预测爬坡功率曲线，实线的为调整后的爬坡功率曲线，通过提前预测到高爬坡率出现，以提前进行预防处理，提前爬坡，当处于爬坡率上升阶段，提前预防处理，能够提前升高功率，防止功率的极速变化，从而降低了爬坡率；当处于爬坡率下降阶段，提前处理能够提前降低功率，防止风电机组的惯性造成的机械和电气磨损等故障，有利于提高风电机组的稳定性，从而提高整个风电场的稳定性。

图12 调整后的爬坡率

图12位改善后的风电爬坡率图，可以看出，应用文中提出的风电场控制策略模型，可以有效地预防高爬坡率出现，将高爬坡率阶段转换成风电机组能够承受的低爬坡率段，从而减少风电机组出现故障的概率，延长风电机组的使用寿命，提高整个风电场运行的可控性和稳定性，降低对电网的影响。

5 结束语

对风电爬坡采取有限度控制策略可以提高风电机组出力的平稳性，给电力系统运行带来积极的影响。文中针对风电功率爬坡问题，在爬坡控制策略上，以单个风电场为研究对象，提出了基于时间序列相似性度量方法和模糊C均值的风电机组的聚类方法，同时给出了基于优先级排序的各类风电机组的有限度控制量化方法与控制策略。算例结果表明，提出的控制策略可以有效地预防高爬坡率出现，延长风电机组的使用寿命，提高整个风电场运行的稳定性和可控性，减少风电对电网的影响。