K-L变换观测矩阵优化算法

王海艳，佟 岐，连志鹏，汲清波

1.哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001

2.北京航天发射技术研究所，北京 100076

1 引言

传统的奈奎斯特（Nyquist）采样定理表明为了不失真的重构出模拟信号，离散信号系统的采样频率必须至少是模拟信号带宽的两倍。然而随着人们对信息需求量的增加，信号带宽也随之不断的增加，导致人们对信号的采集变得越来越困难。近年来由Candès、Donoho和华裔科学家Tao等人提出的压缩感知（Compressed Sensing，CS）理论[1-2]，不受奈奎斯特采样定理中采样速率至少是信号带宽两倍的局限，该理论通过投影观测得到较少观测数据，然后利用重构算法求解优化问题从而高概率地从压缩观测数据中重构原始信号。CS理论直接采集压缩后的数据，避免了先采样后压缩编码而产生大量冗余信息的情况。它在减少冗余数据，节省存储空间上具有较大的优势。

压缩感知理论中包含三个重要组成部分：信号的稀疏表示、观测矩阵的构造、重构算法的设计[3]。其中观测矩阵的构造对信号的重构至关重要，合理的观测矩阵可以高精度的重构出原始信号，目前常用的观测矩阵包括随机高斯矩阵、随机伯努利矩阵、随机傅里叶矩阵等[4]。这些直接构造出的观测矩阵所产生的性能并不是最优的，所以许多学者针对观测矩阵的优化进行了研究。研究表明优化观测矩阵的方法之一是减小观测矩阵与稀疏矩阵之间的互相关性[5]，根据此方法，Xu[6]、Abolghasemi[7]、Tian[8]等人提出了相应的优化观测矩阵的算法，这三种算法都是利用迭代的思想对观测矩阵进行优化，但存在迭代次数较多，运算量较大，并且在观测数据较少的情况下重构图像质量较差的问题。针对这些缺点，本文提出了K-L（Karhunen-Loeve）变换观测矩阵优化算法，该算法通过对传感矩阵（观测矩阵与稀疏矩阵的乘积）进行K-L变换来减小观测矩阵与稀疏矩阵之间的互相关性，从而实现优化观测矩阵的目的。最后通过实验验证了K-L变换观测矩阵优化算法的性能。

2 压缩感知理论

压缩感知的理论基础为信号本身是稀疏的，或者信号在某一变换域是可压缩的，因此信号的稀疏表示是压缩感知理论首要的研究任务。 稀疏信号是指信号本身绝大多数元素为零或近似等于零，或者在某一变换域上绝大多数元素为零或近似等于零的信号。假设x是一个长度为N的实值一维离散信号，记为x∈RN×1。信号x可以稀疏表示成一组正交基的线性组合：

利用一个与稀疏矩阵Ψ不相关的矩阵Φ对信号x进行线性随机投影得到观测量y：

由上式可以很自然地想到利用解线性方程组的方法求解x，但是由于观测矩阵Φ的维度M＜N，所以通过式（2）中y的M 个观测值求解x是一个病态问题，方程无解或有无穷多个解。将式（1）带入式（2）得：

式中，D是M×N(M＜N)矩阵，称为传感矩阵。

因为上式中的s是稀疏的，只有K(K≪N)个值不为零，所以信号的重构表示为：

式中，求解l0最小范数是一个NP难的非凸优化问题。由Candès和Donoho提出的l1范数下的凸优化压缩感知重构框架，将式（4）的非凸优化问题转变成了一个凸优化问题：

通过凸优化算法[9]便可求出s的近优解。

3 K-L变换优化观测矩阵

观测矩阵的设计是为了将信号从N维投影到M维(M＜N)从而获得M个观测值，并保证这M个观测值中包含了重构信号的足够信息，以便可以成功地重构出原始信号或者稀疏系数向量[10]。为了能够从获得的观测值中准确的重构原始信号，Candès和Tao提出并证明了观测矩阵Φ必须满足有限等距性（Restricted Isometry Property，RIP）条件[11]，RIP等距特性在观测矩阵Φ的构造与优化中具有重要意义[12-13]。但是RIP等距特性很难直接应用，Baraniuk在文献[14]给出了RIP准则的等价条件为观测矩阵Φ与稀疏矩阵Ψ几乎不相关，因此减小观测矩阵与稀疏矩阵之间的互相关性可以提高信号的重构概率。

对于观测矩阵的优化，首先将观测矩阵与稀疏矩阵之间的互相关系数μ定义为：

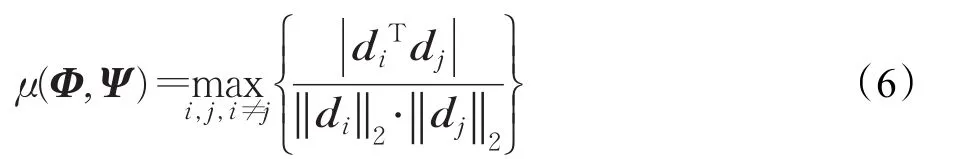
式中，di、dj为传感矩阵D中的任意两列向量。互相关系数μ代表着观测矩阵与稀疏矩阵之间的相关性，μ的值越大代表两个矩阵的相关性越大，那么重构出的原始信号质量越差，为了能够较高精度的重构原始信号，希望μ的值尽量减小。同时，互相关系数还影响着信号的可稀疏度界限[15]。

式（7）表明观测矩阵与稀疏矩阵之间的互相关性越小，则稀疏系数s的上界限越大，所以越有利于原始信号的重构。本文的主要思想是通过对传感矩阵D进行K-L变换，来减小观测矩阵与稀疏矩阵之间的互相关性。

K-L变换又称为特征矢量变换或霍特林（Hotelling）变换，它是以原始数据协方差矩阵的特征向量构成的正交矩阵作为变换矩阵，对原始数据进行正交变换。用原始数据协方差矩阵的特征向量构成的正交矩阵作为变换矩阵，会使变换后数据的协方差矩阵中除对角线之外大部分协方差等于零或者近似等于零，即原来像素间的相关性在很大程度上被减弱。K-L变换的原理是设为N×1维随机矢量，mX=E(X)和分别为其平均值向量和协方差矩阵，ei和λi分别为CX的特征向量和特征值，其中i=1,2,…,N，则K-L变换式为Y=AX。其中变换矩阵A的每一行为协方差矩阵CX对应于特征值λi的特征向量，即

式中，eij(i,j=1,2,…,N)表示第i个特征向量的第 j个分量，满足A×AT=I，其中I表示单位阵。

根据K-L变换式Y=AX得到Y的平均值为：

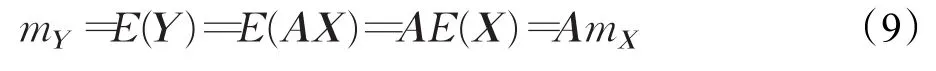
Y的协方差矩阵为：

因为A×AT=I，所以Y的协方差矩阵进一步化简为：

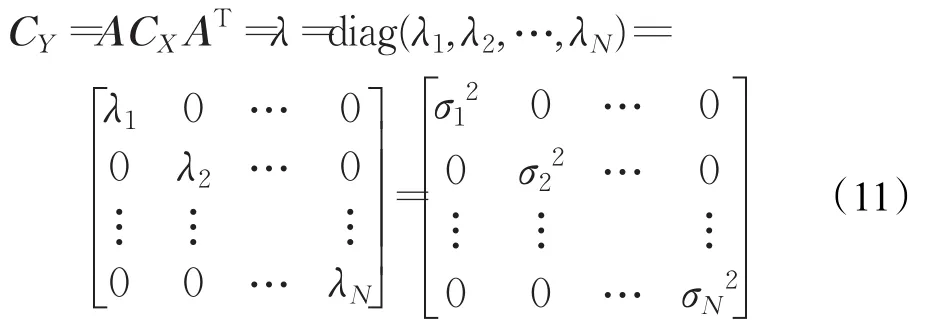
由上述推导得到变换后的矢量Y的协方差矩阵是对角矩阵，除对角线以外其他的元素全部等于零，即

在协方差矩阵中主对角线上的元素σi2(i=1,2,…,N)表示各分量的方差，它代表着各分量能量的大小以及离散程度。方差越大分量的能量越大，分布越离散，而主对角线以外的元素表示分量Yi与分量Yj之间相关程度的协方差，对角矩阵表明了经过K-L变换得到新的分量Yi与Yj彼此之间的相关性在很大程度上被减弱，对角矩阵中主对角线上的方差分布为从大到小，即代表变换后的矢量Y中前面分量比后面分量的能量大，离散程度高。

变换后的矢量为Y=(Y1,Y2,…,YN)T，Y中各分量如下所示：

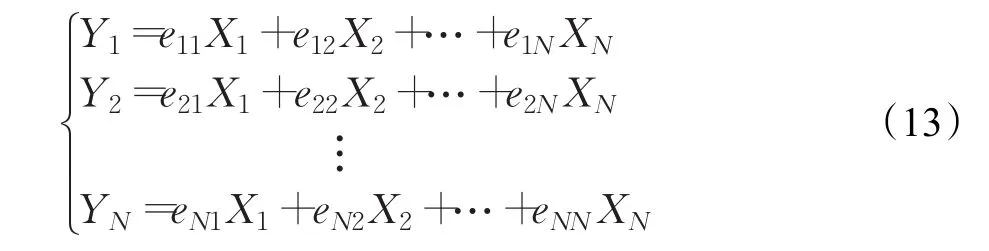
由上式看出，实际上K-L变换是使原始矢量X中各个分量加上一个权重系数，实现线性变换，重新组合成了矢量Y。它是综合了原来各个分量的信息，并不是对原始矢量进行简单的取舍，从而使矢量Y可以较好的反映事物的本质特征。

由于K-L变换是对一维信号的变换，所以在对二维图像信号进行变换时，本文将图像按照每一行都为一个一维信号的原则，从上到下依次对图像的每一行进行K-L变换，具体方法如下所示：

这样便可以使用K-L变换对M×N维传感矩阵进行变换，进而得到优化后的观测矩阵。

K-L变换优化观测矩阵的步骤如下。

1.初始化i=1；

a.将传感矩阵D的第i行转置得到d′，计算d′的均值u=E(d′)，协方差矩阵Cd′=E{(d′-u)(d′-u)T；

b.Cd′Vj=λjVj，1≤j≤N ，式中 λj是特征值并且 (λ1＞λ2＞…＞λN)，相应的特征向量是 Vj，特征向量矩阵为V=[V1V2…Vn]；

c.将V 正交化得V*，变换矩阵A=V*T；

d.变换后的 d′=V*T(d′-u)=A(d′-u)；

e.变换后的传感矩阵D(i,:)=d′T；

2.i=i+1，如果 i=I，则执行（3）；否则执行第1步的a；

3.更新 DI=D(i,:)；

4.计算ΦI=DI×Ψ-1；

输出：优化后的观测矩阵Φ=ΦI

4 实验结果

为了验证所提算法优化观测矩阵的有效性和可靠性，本文选取一幅大小为256×256的Lena图像进行仿真实验。实验中稀疏矩阵Ψ选取DCT稀疏基，重构算法选用凸优化类算法中的BP算法[9，16]，本次实验中定义M=102，即观测矩阵的大小为102×256，采样率r≈0.4，分别用随机高斯矩阵和本文算法优化后的随机高斯矩阵作为观测矩阵，对Lena图像进行仿真实验，得到的仿真效果图如图1所示。

图1 优化算法在采样率为0.4时重构图像效果图

从图1仿真结果可知，利用本文算法优化后的观测矩阵重构图像的PSNR值大于利用未优化的观测矩阵重构图像的PSNR值，这里以PSNR值的大小来衡量图像重构质量的优劣，比较重构出的两幅图像可以看出由本文算法优化后的观测矩阵重构出的Lena图像具有更加清晰的轮廓。由以上分析可知，所提优化算法可以对观测矩阵进行优化。

在以上实验的基础上，只改变观测数目M的大小来验证本文算法优化观测矩阵的可靠性，表1中列出了在M为26～126的情况下，分别利用优化后的随机高斯矩阵和未优化的随机高斯矩阵为观测矩阵重构出Lena图像的PSNR值。从表1中可以看出随着观测数目的增加，由两个观测矩阵重构图像的PSNR值都随之增大。但是在不同的观测数目下，利用本文算法优化后所得观测矩阵重构图像的PSNR值始终大于未优化的随机高斯矩阵重构图像的PSNR值，即证明了利用所提优化算法优化观测矩阵的可靠性。

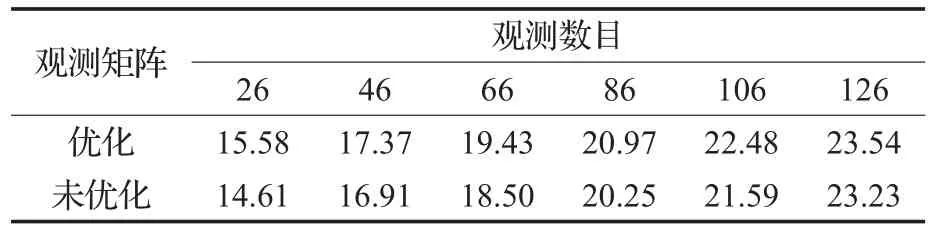
表1 不同观测数目下优化后观测矩阵与未优化观测矩阵重构图像的PSNR值比较

为了进一步说明所提优化算法的性能，继续进行本文算法和Xu算法、Vahid算法以及Tian算法的比较实验，本次实验选取两幅大小均为256×256的Lena图像和Mandi图像进行仿真实验。实验中稀疏矩阵Ψ依然选取DCT稀疏基，观测矩阵Φ分别选用本文算法、Xu算法、Vahid算法以及Tian算法，重构算法依然采用凸优化类算法中的BP算法，用PSNR值的大小来代表两幅图像的重构质量。本次实验在采样率r=0.5的情况下，得到的仿真结果如图2所示。

从图2和图3可以明显的看出，用本文算法优化后的观测矩阵重构图像的PSNR值大于用其他三种算法优化后的观测矩阵重构图像的PSNR值。从图中可以看出，由本文算法优化后的观测矩阵重构出的图像具有更加清晰的视觉效果，重构的两幅图像帽子边沿、眼睛以及胳膊等部位的轮廓更加清晰，这说明相比较其他三种优化算法优化的观测矩阵，用本文算法优化后的观测矩阵重构图像的质量和视觉效果最好。

图2 不同算法在采样率为0.5时重构Lena图像效果对比

图3 不同算法在采样率为0.5时重构Mandi图像效果对比

表2为在采样率r=0.5时，重构算法为凸优化类算法中BP算法的情况下，对两幅大小为256×256的Lena图像和Mandi图像进行仿真实验，对比各算法对图像重构时间的长短。从表2中可以看出，与Xu算法、Vahid算法、Tian算法优化后所得观测矩阵以及未优化的随机高斯矩阵重构图像所用的时间相比，利用本文算法优化后所得观测矩阵重构的两幅图像所用的时间最短。这意味着，和文中所提其他优化算法相比，本文算法在不增加重构时间的基础上可以得到更高质量的重构图像。

表2 不同算法在采样率为0.5时重构图像时间对比

对比四种算法优化后的观测矩阵以及未优化的随机高斯矩阵，在采样率为0.2～0.65之间对Lena图像和Mandi图像重构的重构误差值，两幅图像重构误差曲线图如图4所示。

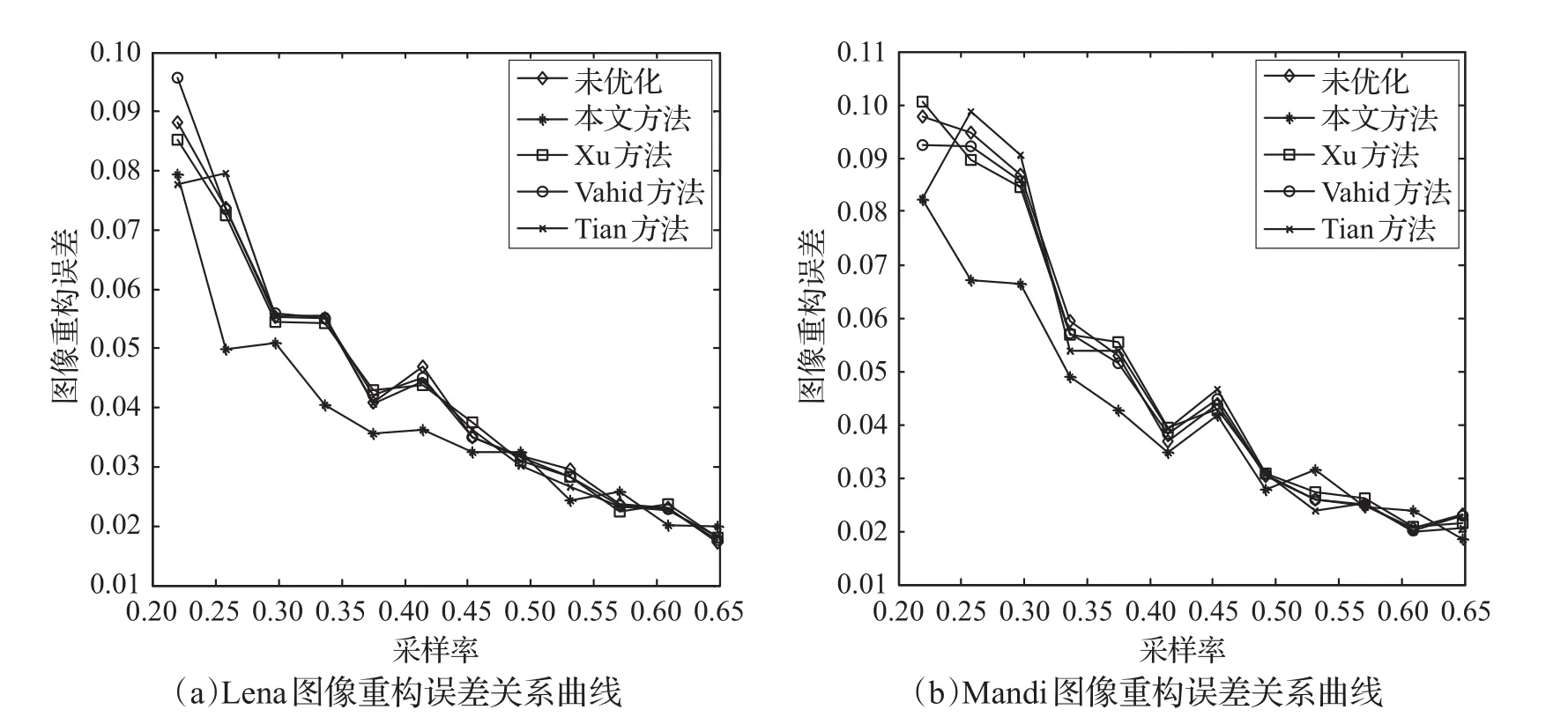
图4 各优化算法在采样率为0.2到0.65之间两幅图像重构误差关系曲线

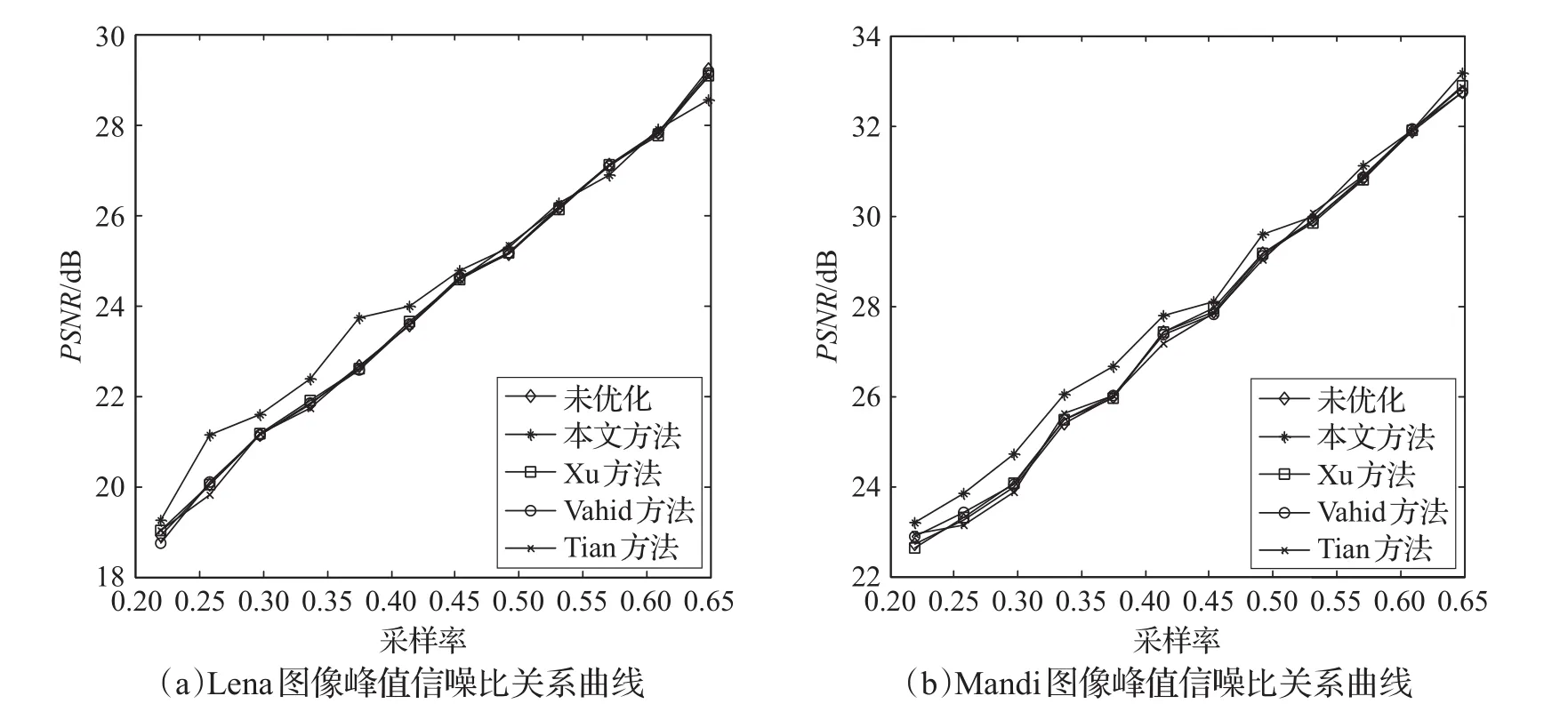
图5 各优化算法在采样率为0.2到0.65之间两幅图像重构的峰值信噪比关系曲线

从图4可以看出，在采样率为0.2～0.65之间，随着采样率的增加4种算法优化后的观测矩阵以及未优化的随机高斯矩阵对于图像的重构误差都逐渐减小。在采样率为0.2～0.5之间，利用本文方法优化后的观测矩阵与另外三种方法优化后的观测矩阵以及未优化的随机高斯矩阵相比具有更低的图像重构误差，图像的重构误差越小代表着图像的重构质量越高。由仿真图可知，在采样率为0.5～0.65时，相比于另外三种方法优化后的观测矩阵以及未优化的随机高斯矩阵重构图像的重构误差，利用本文方法优化后的观测矩阵重构图像的重构误差存在优劣交替的不稳定现象。两幅图像重构的峰值信噪比值曲线图如图5所示。

从图5中可以看出，所有的方法重构得到的PSNR值都随着采样率的增加而增大，这是因为采样率增加所得到的观测数目随之增多，采样得到原始信号的信息也会随之增加，所以重构信号的PSNR值越大，即重构质量越好。相比较来说，本文方法在采样率为0.2～0.5的时候重构质量最好，这说明使用本方法重构的观测矩阵在较少的观测数据下就可以较好的重构出原始信号。由仿真图可知，在采样率为0.5～0.65时重构质量几乎持平于Xu方法、Vahid方法以及Tian方法。通过分析以上仿真实验结果，得出了在观测数目较少的情况下，本文算法相对于文中所提其他算法对图像的重构具有更好的效果。

5 结束语

根据减小观测矩阵与稀疏矩阵之间互相关性的思想，本文提出了利用K-L变换减小观测矩阵与稀疏矩阵之间的互相关系数来优化观测矩阵的方法。通过对实验结果进行分析，本文提出的观测矩阵优化算法能够对观测矩阵进行优化，利用本文所提优化算法优化后的观测矩阵重构出的图像具有较高的精度，尤其是在采样率较小时本文提出的优化算法相对于其他优化算法的优势更加明显，这将为今后在压缩感知方面的研究工作提供一定的参考。