博弈选择模型在步态识别中的应用研究

柴艳妹，韩文英，王 坚，王友卫

中央财经大学 信息学院，北京 100081

1 引言

近年来，基于信息融合理论的生物特征识别算法已成为该领域最为活跃的研究方向之一。与单特征算法相比，多特征融合可以提供关于被测对象更为全面、完整的信息，从而有效提高识别算法的准确率。以步态识别为例，当前典型的特征融合算法包括四类：静态特征和动态特征的融合；非结构特征和结构特征的融合；多视角特征的融合[1]；多模态特征的融合[2]。其实无论哪种类型的融合，都需要对不同信源的特征进行甄选，既要保证不同类型特征之间的互补性，也需要考虑同类特征之间的冗余性。但从目前发表的文献来看，为了进一步提升识别性能，大多数的研究工作仍着眼于尝试新的特征提取算法和新的融合机制。例如Ahmed等人[3]提出用关节相对距离（JRD）和关节相对角度（JRA）作为步态特征，并用遗传算法度量它们之间的相关性，进行了决策级融合；Triloka等人[4]则构建了一个基于多层负反馈的神经网络系统，将肌电图信号和视频采集到的小腿神经肌肉信号进行融合，用以分类；孙楠等[5]采用改进的粒子群优化MPSO-BP神经网络方法识别不同运动模式下的人体步态相位，也取得了较好的识别效果。这些新的特征提取算法和融合机制往往需要使用更复杂的技术和架构，甚至耗费更多的算力来换取识别率上的些许提高。事实上，这方面的研究已遇到瓶颈。

目前，很少有人尝试从特征选择的角度来研究这个问题，即如何在众多已有的类似特征中选择出最优的特征组合进行融合，从而提高识别性能。特征选择作为一种数据处理手段近年来被广泛研究，并应用到了各行各业中。在早期的研究中，各种度量手段作为评估函数被应用到特征选择算法，如信息论度量、关联度量、一致性度量、距离度量和依赖性度量等。典型的算法如Yu等人[6]2004年提出的FCBF方法，使用了信息论中的对称不确定性来衡量两个特征的相关性，并结合Markov blanket技术删除冗余特征；Peng等人[7]2005年提出的mRMR方法，利用互信息理论来兼顾特征和类别之间的相关性以及特征之间的冗余性。这类方法在考虑冗余问题时，都是计算成对特征的冗余性，而没有考虑到特征加入或删除后特征子集组合效应的变化。因此，近年的研究中特征的组合效应越来越被重视。例如，Dong等人[8]使用进化算法，杨昙等人[9]使用群体智能，段洁等人[10]提出基于粗糙集依赖来度量特征子集的组合效应；而Sun等人[11-12]也将合作博弈理论中的班次哈弗权利指数以及夏普利值运用到特征选择方法中，用以评估特征在整个子集中的组合影响力。但这类方法在构建候选子集时复杂度高，需付出大量的时间代价。

在多源信息融合中，信源间的差异性是普遍存在的。因此，不同信源间不但有互补关系，也存在冗余和冲突。以一个静态特征和动态特征的步态融合为例，静态特征可选取人体形状的描述，比如身高、体宽、紧致度、矩形度和伸长度等；而动态特征则可以选取身体各部位的动态时变信号，比如区域面积和区域方差等。一方面，同类特征之间有较大的冗余性，如果将这些特征全部进行融合会使样本集特征空间维数过大，并且造成噪声的二次引入，从而影响识别的效率和精度；另一方面，异类特征之间不仅具有互补性，也可能存在潜在的冲突，例如身体各部位的区域面积特征实际上也蕴含着被测对象的身高和体宽等信息。这些冲突关系也可能会影响融合算法在步态识别中的处理性能。

从上述分析来看，由于传统特征选择方法在构建候选子集时复杂度高，需付出大量的时间代价，因此很少有人考虑将其运用到多生物特征融合的识别领域。然而，步态特征融合过程中存在的不仅仅是选择特征的问题，更重要的是如何解决特征之间的合作和冲突。博弈论是一门完整的决策理论，主要研究在多个参与者参与的对抗性或合作性活动中，博弈的参与者应采取何种合理的策略，以取得有利的个人利益或联盟的集体利益。将博弈论和信息融合理论相结合是新的尝试，本文构建了新的博弈特征选择模型，通过定义支付函数大大降低了选择最优特征组合的计算量。下文将详细描述博弈选择特征模型的构建和求解方法，最后用步态识别的示例和实验验证模型的有效性。

2 博弈特征选择模型

博弈论模型是从人类社会的政治、经济、军事等活动中抽象出来的一种数学模型。从19世纪发展至今，它形成了很多种分类，如技能博弈、自然博弈以及策略型博弈等。和步态融合问题比较吻合的是策略型博弈模型。

2.1 策略型博弈模型

构成策略型博弈模型的三要素是局中人、策略和支付函数。

定义1局中人指参与博弈的对象，可以是两个或多个，记为Pi。所有局中人构成的集合称为局中人集合，记为，其中N是参与人或局中人的个数。

定义2策略指局中人所选择的行动。用sj(j∈n)表示局中人Pi所拥有的n个策略中的某一个，则局中人Pi的所有策略的集合称为该局中人的策略集，记为Si(i∈N)。

定义3支付函数指局中人Pi的定义在策略组合集合S上、取值于实数空间R的一个函数，记为ui()s，用以描写局中人Pi在策略组合s∈S之下所获得的某种收益或所遭受的某种损失。

定义4当以上三种要素都已明确，那么就可以用表示一个策略型博弈模型。在策略型博弈模型中，如果每个局中人对于N,S1,S2,…,SN,u1,u2,…,un都了解，那么该模型是信息完全的。如果N个局中人同时选择策略，那么该模型是静态的。

定义5设为一完全信息的静态博弈模型，称策略组合，并且为一个纳什均衡。如果对∀i∈N ，是在条件下局中人Pi的最优选择，即

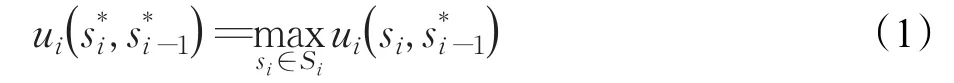
2.2 构建步态融合中的博弈选择模型

根据博弈论思想，在进行步态融合特征选择时可以将存在冗余和互补关系的特征空间中的特征选择看作是步态特征间的博弈问题。博弈的目标是在众多同类和异类特征中找到最佳的特征组合用于融合分类，从而提高步态识别的算法性能。

2.2.1 局中人设计

在博弈特征选择模型中，可以把同类的、具有冗余关系的步态特征定义为同一个局中人，把异类的、具有互补关系的步态特征定义为不同的局中人。例如，动态步态特征和静态步态特征可分别定义成局中人P1和局中人P2。

2.2.2 策略设计

第Pi个局中人的某个策略sj可以定义成具有冗余关系的同类特征中的某一个特征。因此，该类特征（即局中人Pi）的策略集为Si={ }s1,s2,…,sn，其中n为第i个局中人所拥有的特征个数。

2.2.3 支付函数设计

支付函数在博弈模型中起着至关重要的作用，它是计算博弈局中人收益、构建博弈矩阵进而求取均衡解的基础。因此，支付函数的准确程度关系到博弈结果的准确程度。在信息融合系统中，单信源所提供特征往往是不完整或不精确的；多信源特征或许可提供互补信息，但也可能提供不同置信度的冗余信息，甚至是矛盾或冲突信息。融合系统不得不依据这些具有不确定性的信息进行推理，以达到决策和控制功能。在步态特征的博弈选择模型中，支付函数值应能反映出局中人的冲突关系和分类能力，并能对其进行可信度量。信息论中的熵作为不确定性度量，有着其他方法无法比拟的优势。

（1）信息熵：对于在给定论域上的随机变量X，其概率分布为，则：

其中，k是一个取决于度量单位正常数。信息熵表征了信源整体的统计特征，是总体的平均不确定性的度量。

（2）条件熵：用来表示二维概率系统中，在已知一个随机变量情况下，对另一个随机变量不确定性的度量，公式如下：

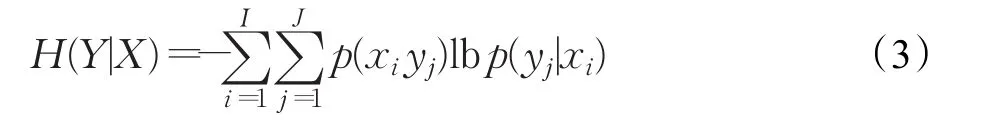
条件熵又称信道疑义度，当随机变量X和Y分别表示信息传递系统中的输入变量和输出变量时，H(Y|X)表示在输出端接收到信息Y后，对输入变量X尚存的平均不确定性，即，条件熵描述了输入信号和输出信号之间的依赖关系。

（3）平均互信息：由于事物之间的相互联系，使得在已知随机变量Y的情况下，对X的平均不确定性的消除程度可用平均互信息来表示。

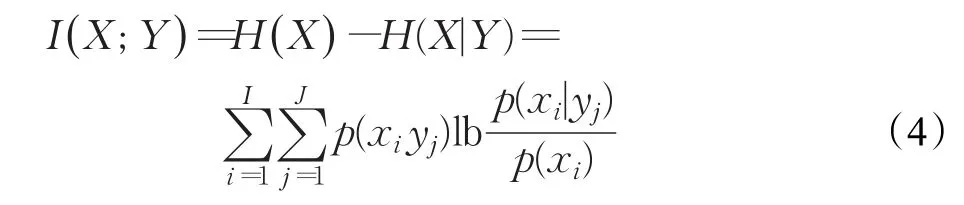
在博弈选择模型中，支付函数的设计首先应能表现出局中人之间的对立统一关系；其次要能区分出不同策略的分类能力，分类能力强的策略支付值大。因此，本文利用信息熵表示策略分类能力的大小，采用平均互信息表示信源间的冲突。其中，H(X)和H(Y )分别表示特征X和Y的信息熵，即局中人选取某一特征进行融合时，这一策略对系统正确分类的能力。平均互信息I(C ;X )表示在已知特征X的情况下，对分类信息C的平均不确定性的消除程度，即特征X对分类C的可信度。则特征X和Y可信度之间的冲突可以用[I(C:X)-I(C:Y)]表示。构造的支付函数如下：

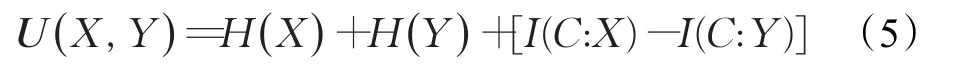
3 博弈选择模型在步态融合中的应用示例

经过多年的研究和发展，步态识别领域已积累了大量特征提取算法。为了验证上述模型的有效性，示例特征的选取既要考虑同类特征间的冗余性，也考虑异类特征间的互补性。因此，本文将以3个经典的人体轮廓描述特征（紧致度、矩形度和伸长度）和2个动态区域描述特征（区域方差和区域面积）为例进行实验。

3.1 特征提取

人体轮廓是步态识别的重要特征之一，也是现实生活中人类视觉系统识别人的主要依据。描述人体整体轮廓的方法有很多种，这里引用了3种较常用的特征[13]。

（1）紧致度

紧致度是抽象代数的概念，其中，L表示轮廓周长，A表示轮廓的面积。在静止状态下，紧致度在一定程度上反映了人的高矮胖瘦等物理形态，而人在行走的时候骨骼和肌肉的变化也是会反映到轮廓上来的。因此，一个轮廓序列的紧致度是可以表达人体的步态特征的。

（2）矩形度

矩形度是轮廓与其外接矩形的面积之比，其中，H表示轮廓的高度，W表示轮廓的宽度，A表示轮廓面积。它反映了人在行走时，其相对于外接矩形的松紧程度，间接反映了人走路时的步幅和步距。

（3）伸长度

其中，H表示轮廓的高度，W表示轮廓的宽度。事实上，轮廓的高度和宽度隐含了目标的高矮胖瘦信息。但是这两个参数常常随着摄像机拍摄距离的变化而变化。例如，同样焦距下，一个高个子目标由于拍摄距离较远会显得比近处的矮个子目标还要矮小。宽度所代表的胖瘦信息也是如此。因此，它们都不可以单独作为形体特征来进行步态识别。为了消除这种误差，可用伸长度来描述人体的轮廓特征。

仅以人体轮廓作为步态特征，粒度过大。据观察，人在走路过程中，身体不同部位的运动特征是不一样的，为了捕捉这种差异，可以提取身体不同部位的步态特征。为此，可先将人体侧影按照身体比例划分为头、身体和腿3个区域（见图1），然后分别计算不同身体部位在走路过程中的方差和面积变化特征[14]。

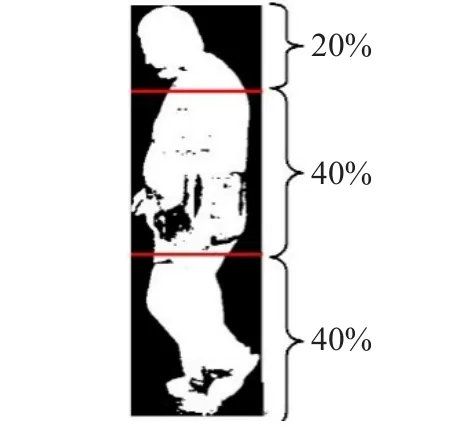
图1 人体区域分割比例图

（4）区域面积

其中，R1表示头部，R2表示躯干，R3表示腿部，fk(i,j)代表某个区域(k=1,2,3)中位置(i,j)处的像素值，且f(i,j)∈{0,1}。由于区域是固定的，因此当身体某一部分在走路过程中有较大幅度运动时，前后几帧图像在该区域中呈现出来的目标面积会随之改变，从而体现出步态的运动特征。

（5）区域方差

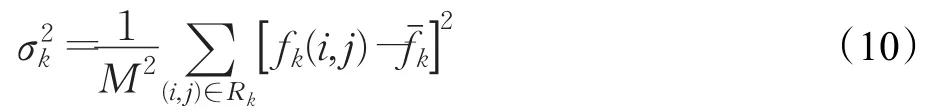
3.2 博弈选择模型

这里选用的特征既有明显的互补性，也有暗藏的冗余和冲突性。紧致度、矩形度和伸长度都是对人体轮廓的整体描述，使用了宽度W、高度H和面积A等信息，特征之间具有较大的冗余性，可以归为一类；而区域面积和区域方差反映的则是步态的运动特征，它们的计算很类似，特征之间也具有较大的冗余性，可以归为另一类。同时，两类特征一个是对步态的静态描述，粒度较粗；另一个是对步态动态特征的描述，粒度较细，它们之间存在明显的互补性，因此可用于特征融合算法，以提高识别性能。但是如果将五类特征直接进行融合，会使样本集特征空间维数过大，并且冗余特征会造成噪声的二次引入，从而影响识别的效率和精度。另一方面，这两类特征之间不仅具有互补性，也可能存在潜在的冲突，例如身体各部位的区域面积特征实际上也蕴含着被测对象的身高、体宽和面积等信息。这些冲突关系也可能会影响融合算法在步态识别中的处理性能，因此，如何在不用穷举的情况下，找到最佳的融合特征组合正是本文研究的目标。

（1）局中人

把同类的、具有冗余关系的步态特征定义为同一个局中人；把异类的、具有互补关系的步态特征定义为另一个局中人。即局中人P1用来描述细粒度的动态区域特征，而局中人P2则用来描述粗粒度的人体轮廓特征。

（2）策略

S1={区域面积，区域方差}用来描述局中人P1所能采取的策略；S2={紧致度，矩形度，伸长度}用来描述局中人P2所能采取的策略。

（3）支付函数

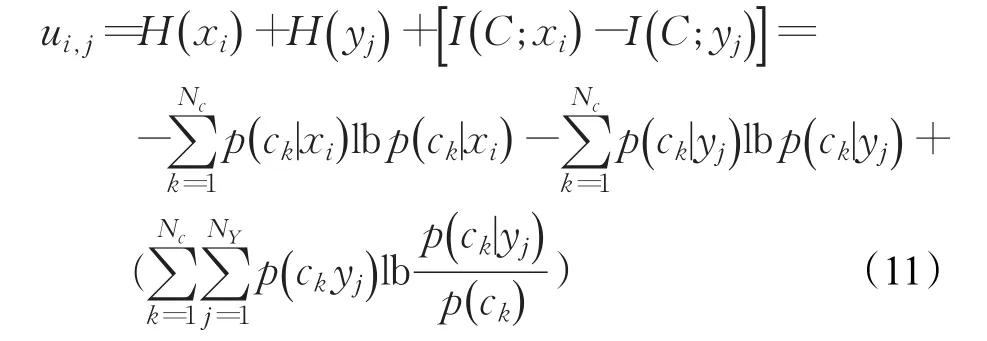
（4）均衡点求解

为了选择最佳策略，局中人可使用极大化极小原理（即行的最小值和列的最大值），也就是说，选择包含着最坏的可能结果中的最佳答案，这样就可保证收益不会低于一个确定的值——极小中的极大值。当然行局中人和列局中人都可采用这个方法，但它们选择的策略可能一致，也可能不一致；如果它们一致，那么这个博弈就有均衡点，即最优解。如果它们不一致，这个博弈没有均衡点，即纯优策略不存在。这时可以根据实际应用情况给各策略分配一个概率值，即求取极小化极大混合策略的值。关于博弈矩阵的均衡点求解问题可参看文献[15]。

4 实验结果分析

4.1 实验数据库

采用两个国际上通用的步态数据库进行实验，它们分别涵盖了数据库的室内/室外、快走/慢走以及数据规模大/小等因素对自动步态识别的影响。

（1）Carnegie Mellon University（CMU）数据集：由25个人组成，分快走、慢走、倾斜和抱球4种方式。本文分别实验了快走和慢走两种方式的侧视序列，每个序列7～8个步态循环。室内拍摄，人离摄像机较近。

（2）中科院CASIA Dataset B：有124个受测者，分别考虑了视角、衣服和带物3种情况的变化，所有视频均是在室外的远距离拍摄。本文实验了107个受测者“e090”视角的步态序列。实验所用数据示例图，如图2所示。

图2 实验数据示例图

4.2 实验方案

为了验证博弈选择模型的有效性，设计如下实验方案：

（1）首先根据3.2节所述方法求取支付函数矩阵；

（2）利用极大化极小原理求解均衡点，均衡点所在位置，即最佳融合策略；

（3）分别在CMU数据库和CASIA数据库上对所有特征进行穷举组合，并利用特征级融合方法得到其融合识别结果；

（4）对比实验结果，判断博弈选择模型得到的最佳组合是否具有最好的识别结果。

在特征提取之前，CMU数据库和CASIA数据库中的图像都经过了二值化、模板提取和周期性分析等预处理，并采用最近邻分类器（NN）进行模式分类。由于步态数据具有周期性、循环性的特征，相似性度量则采用基于周期的算法，具体做法见文献[16]。分类性能的评价采用模式识别领域常见的累计匹配分值（CMS）和相关操作特征（ROC）曲线。

4.3 最佳融合策略

对于CMU数据库，将数据库中每个样本序列按照步态周期拆分为若干子序列（每个快步走序列大约包含8个步态周期，每个慢步走序列大约包含7个步态周期），再每人随机抽取一个步态周期作为训练集，其余步态周期序列作为测试集，来进行步态识别。首先，分别计算5类特征单独作为步态特征进行识别时得到每一类别的条件概率。然后，再根据博弈选择模型支付函数的计算方法，计算其支付矩阵。进一步，利用极大化极小原理（即行的最小值和列的最大值）找到博弈矩阵的均衡点。

可以看出，两个矩阵的均衡点均在x1y3处，即局中人取“区域面积”，局中人2取“伸长度”的位置。也就是说，按照博弈选择模型，在CMU数据库中将“区域面积”和“伸长度”进行特征融合，可取得最优的融合效果。

而对于CASIA数据库的“e090”视角数据集，也可采用同样的周期拆分处理方法，随机抽取107个子序列作为训练集，剩余的535个子序列作为测试集，来进行步态识别。采用和CMU数据库上同样的算法，计算支付函数，并利用极大化极小原理找到博弈矩阵的均衡点。

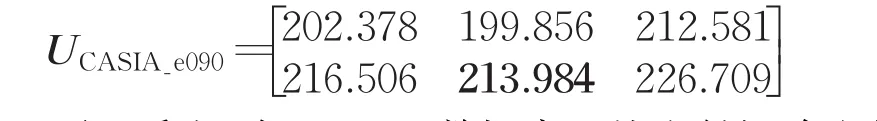
可以看出，在CASIA数据库上的支付矩阵也找到了博弈均衡点，该均衡点在x2y2处，即选取“区域方差”和“矩形度”特征进行融合，可取得最优的融合效果。

4.4 实验结果比较

为了验证该方法的有效性，本文对局中人1和局中人2的策略进行了穷举法融合，并给出了特征集融合方法下的平均识别率进行对比。实验结果如表1～3所示。

4.5 实验结论及分析

对实验结果进行深入分析，本文得到以下结论：

（1）从表1和表2中最近邻分类器的识别率来看，在CMU数据库中的快走和慢走数据集上取得了一致的实验结果，即“区域面积+矩形度”和“区域面积+伸长度”均得到了较高的识别率。再仔细观察图3（a）可以发现，CMU快走数据集上在CMS横坐标约为7的位置，“区域面积+伸长度”的识别性能略有优势，因此进一步评价了CMS取10以内的平均识别率，发现CMU快走数据集上“区域面积+伸长度”更优一些，而在CMU慢走数据集上两者基本持平（见图4）。这和博弈选择模型得到的结论基本一致。

（2）从表3中最近邻分类器的识别率来看，“区域方差+矩形度”和“区域方差+伸长度”均取得了较高的识别率。再进一步通过CMS取5以内的平均识别率，可以发现“区域方差+矩形度”的识别性能更好一些，而图5（b）中ROC曲线也证明了这一结论。这和博弈选择模型的结论也是一致的。

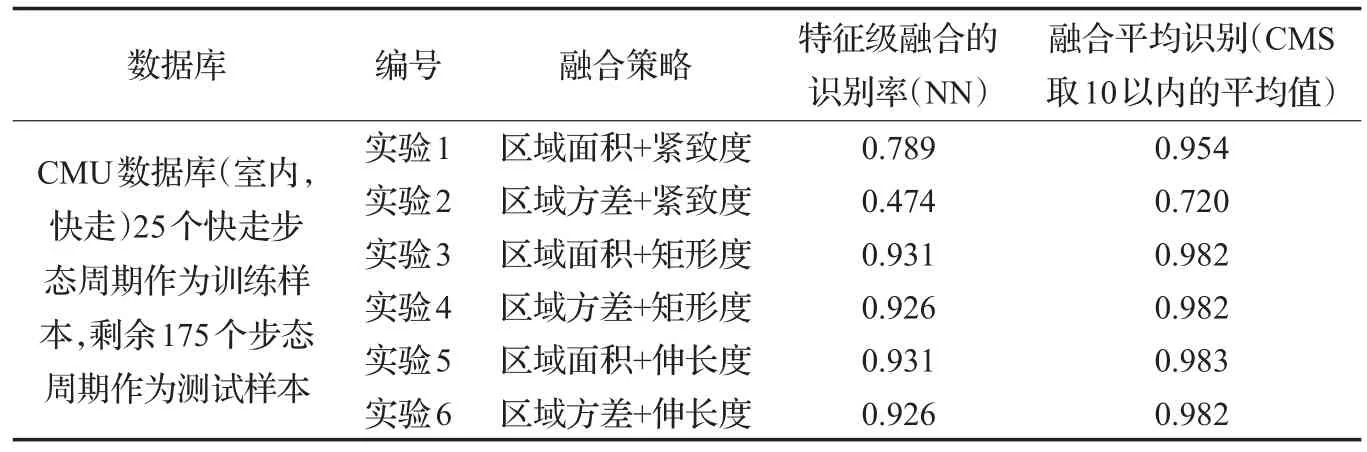
表1 CMU快走数据集上的实验结果比较

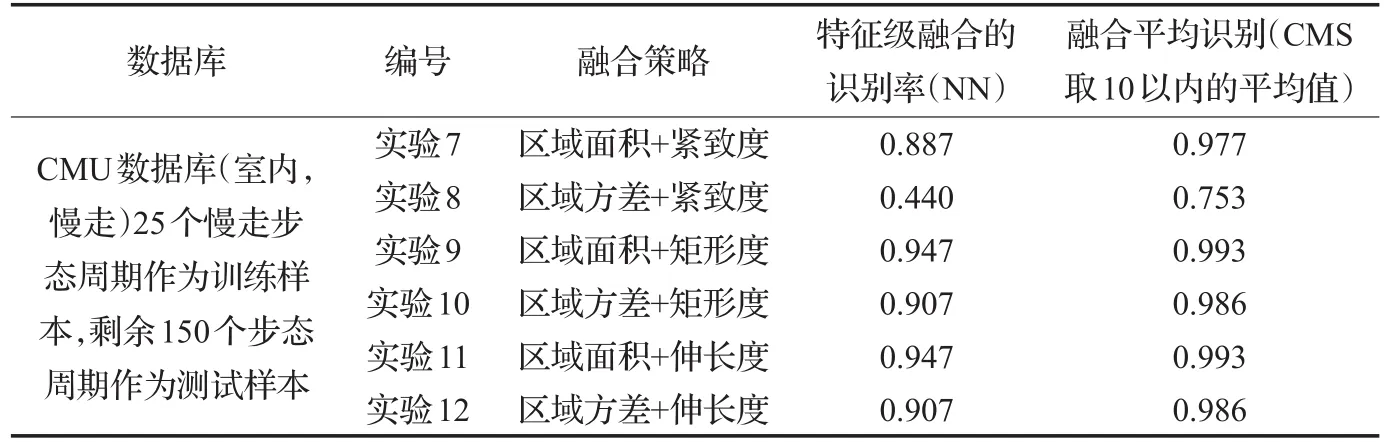
表2 CMU慢走数据集上的实验结果比较

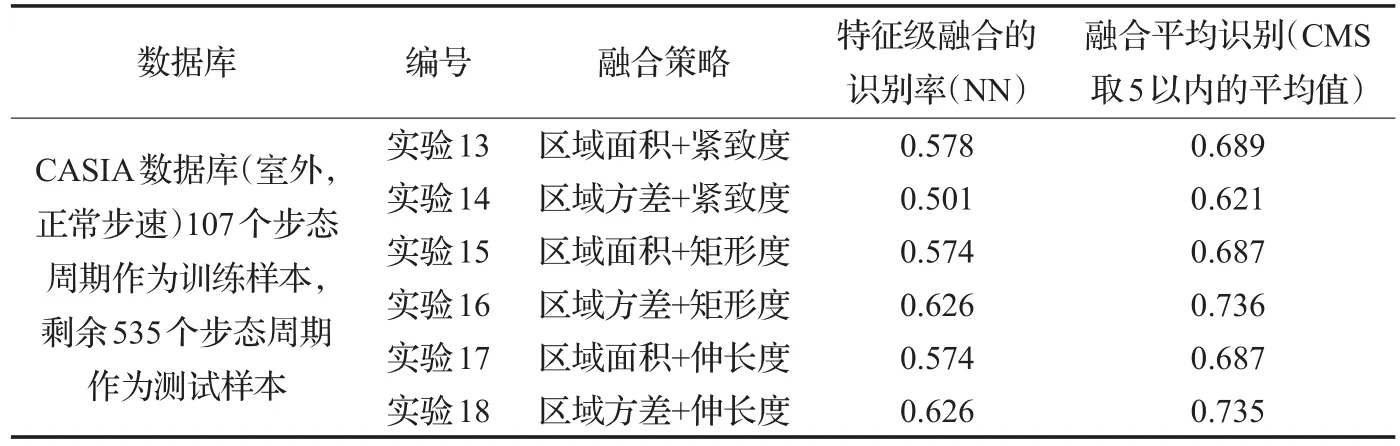
表3 CASIA数据集上各融合策略的融合结果比较

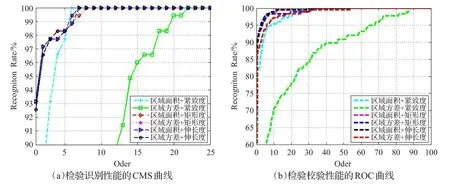
图3 CMU快走数据集的识别校验性能曲线

图4 CMU慢走数据集的识别校验性能曲线

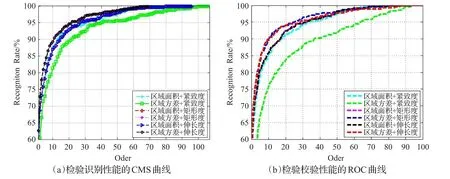
图5 CASIA e090数据集的识别校验性能曲线

（3）从上述分析来看，可以肯定本文提出的博弈选择模型是行之有效的。进一步综合分析表1～3的实验结果发现，“矩形度”和“伸长度”这两个特征分类性能极为类似，且结果较“紧致度”要好很多，因此，局中人2选“矩形度”或“伸长度”都可以。而“区域面积”和“区域方差”的分类性能在不同的数据库上各有优势，使用博弈选择模型可将其有效选出。

（5）本文所设计的18个实验不仅涵盖了室内/室外不同的应用场景，还测试了快走/慢走不同的目标情况，并在样本规模不同的两个数据库上进行了实验。从表1～3的实验结果来看，本文结论对不同场景和不同目标均有较好的普适应。

5 结论

本文最大的特点是从特征选择的角度，通过引入博弈论来解决步态特征融合过程中的特征合作和冲突问题。在多特征组成的特征空间中，把具有冗余关系的特征定义为博弈过程中的同一个局中人，具有互补关系的特征定义为另一个局中人。利用信息论中的信息熵和互信息构建了支付函数，使其能表现局中人之间的可信度冲突关系。使用极大化极小原理求得博弈矩阵的均衡点，从而得到融合的最佳策略组合。为了验证该方法的有效性，以冗余度极大且有互补性的3个人体轮廓特征（紧致度、矩形度和伸长度）和2个区域特征（区域方差和区域面积）作为例子进行了实验。从实验对比和分析来看，本文提出的博弈选择模型是行之有效的方法，它可以用较少的计算量得到最优的融合特征组合。但目前所选用的特征都过于简单，下一步将尝试此算法在不同视角及不同模态下的普适性及尝试设计新的博弈支付函数。