基于滑动窗口和ARMA的Argo剖面数据异常检测算法

罗一迪，蒋 华，王慧娇，王 鑫

桂林电子科技大学 计算机与信息安全学院，广西 桂林 541004

1 引言

Argo是第一个实时的、高分辨率的全球立体海洋观测网，因其活跃性和规模，可以说是海洋观测史上的一场革命[1]。自2000年实施以来，所获得的温度、盐度剖面数据量比过去100年收集的总量还多。但是Argo浮标易受到环境的影响，尤其是测量盐度的传感器，容易受到生物污染、生物杀伤剂泄露等原因的影响，造成盐度测量产生误差。而且由于Argo浮标自身的随机性和抛弃性，海洋工作者们很难对其传感器进行校正，也很难确定传感器产生误差的原因，所以很有可能出现数，其中V2表示待测数值，V1、V3表示与V2相邻的上下两个剖面点数据。若测试盐度，则当压强＜500 dbar时，检测值超过0.9 PSU，或者当压强≥500 dbar时，检测值超过0.3 PSU，则待测值据误差或错误。为了进一步服务于科研和其他社会应用，需要对于数据的质量精度有一定的保证，所以Argo剖面数据的异常检测就显得尤为重要。

关于Argo剖面数据的异常检测，有大量的学者做了研究工作。文献[2]提出了一种利用传统阈值剔除异常数据的方法，其所要求的剖面计算公式为：检测值=标记为异常。可以看出，该方法只是针对单一剖面数据进行异常检测，并且没有考虑采样点检测深度间隔的变化。文献[3]采用“三倍标准差”与传统阈值判断相结合的方法实现对Argo剖面数据的异常检测，该方法结合了邻近剖面数据，弥补了传统阈值判定方法的不足，但是该方法采用的是全局静态阈值，当阈值设置不合适时可能造成某些异常剖面点的误判或者漏判。文献[4]将多年的历史温盐观测数据（南森站和CTD资料）通过最小二乘法拟合得到某地区的温盐关系模型，并利用该模型对Argo剖面数据进行质量控制。但是由于温盐数据的非线性的特点，采用最小二乘法无法很好地提取出数据特征，因此获得的温盐关系模型精确度不高，导致异常检测的可靠性也不高。因此，如何对于Argo剖面数据进行有效的异常检测，并且保证较高的精确度和可靠性，是一个重要的研究问题。

异常检测[5]（Anomaly Detection）就是识别出与历史或者预期模式有显著差别的过程，异常数据可能由于传感器采集错误或者数据传输等原因产生。对于异常检测，国内外学者已经做了大量的研究。文献[6]利用滑动窗口划分畜禽物联网数据流，并通过支持向量回归模型实现数据流的异常检测。文献[7]将变压器在线监测数据流通过滑动窗口进行筛选，再使用聚类模型实现了对变压器状态的异常检测。文献[8]利用滑动窗口和LN预测模型获取水文数据的预测值，并通过对比观测值与预测值，实现了对于水文数据的异常检测。通过文献[6-8]可知，利用滑动窗口可以全面有效地挖掘出时间序列的异常点，而且具有较高的精度和可靠性。

ARMA是一种典型的、应用最广的时间序列模型。文献[9]利用ARMA模型实现估计观测噪声方差的目的。文献[10]通过ARMA模型可以有效地探测到地震电离层出现的异常扰动，并且具有较高的精度。文献[11]利用最小二乘法与ARMA模型相结合的方法，实现了对于卫星导航定位和航天器跟踪中重要的极性参数的预测。文献[12]使用ARMA模型预测在线电视剧的流行度，预测结果准确性高，并且具有较高的参考价值。因此，使用ARMA模型可以有效地实现时间序列预测，并且具有较高的预测精确度，是一种理想的预测模型。

基于上述研究，本文采用滑动窗口（Sliding Window，SW）模型与自回归移动平均（AutoRegressive Moving Average，ARMA）模型实现对于Argo剖面时间序列的预测，然后利用中心极限定理（Central Limit Theorem，CLT）获得置信区间，对比待测剖面点的观测值与置信区间之间的关系，实现剖面数据的异常检测。

2 Argo剖面数据异常检测

根据国际Argo计划的要求，每个浮标的循环测量周期是10天，意味着每10天浮标上浮一次[13]，在其循环周期内，浮标测量0～2 000 m水深范围内的温度、盐度数据。因此，Argo浮标剖面数据是包含温度、盐度等属性的时间序列，可以表示为PN={p1,p2,…,pn}，其中 pi=(oi,ti)，表示ti时刻对应的剖面观测值是oi(1≤i≤n)。

本文的Argo剖面数据异常检测算法的基本思想：首先利用滑动窗口划分剖面时间序列，再建立ARMA预测模型，获得剖面数据的预测值，然后利用中心极限定理计算置信区间，通过判断观测数据是否在置信区间内来判断待测剖面点pi是否异常。整个算法的具体描述如下：

算法Argo剖面数据异常检测算法

输入Argo剖面序列PN，k-近邻剖面点序列的宽度k，置信度 p。

输出Argo剖面标记序列

步骤1初始化待测剖面点 pi的k-最近邻窗口ζi=

步骤2建立ARMA预测模型，输入ζi作为参数，计算获得预测值i。

步骤3计算对应的上界和下界

步骤4判定待测剖面点pi是否异常。若，则点 pi为正常点，令 flag=1，跳转至步骤5；否则点 pi为异常点，令 flag=0，跳转至步骤6。

步骤5后移一位滑动窗口，用 pi替代ζi={pi-2k,pi-2k+1,…,pi-1}中的 pi-1，获得新的k-最近邻窗口 ζi+1。

步骤6后移一位滑动窗口，用 pi替代ζi={pi-2k,pi-2k+1,…,pi-1}中的 pi-1，获得新的k-最近邻窗口 ζi+1，并以预测值i替换原有的观测值 oi，即。

步骤7 若i＜n，则i=i+1，跳至步骤2；否则，对PN的异常检测结束，输出

Argo剖面时间序列异常检测算法的流程图，如图1所示。

2.1 滑动窗口及Argo剖面子序列的预测

现有的Argo剖面数据异常检测算法中，多数是利用固定阈值进行判定，但是剖面数据分布会随着环境的变化而变化。若采用固定阈值进行异常检测，当阈值设置过大时，会造成错判，当阈值设置过小时，会造成漏判，所以阈值的设置直接影响着异常检测算法的精度和可靠性。因此本文引入滑动窗口模型，利用滑动窗口选择邻近的多个剖面点来计算预测值，从而可以确定不同的阈值。此外所有的剖面子序列都有可能存在异常数据，而滑动窗口可以遍历所有的剖面子序列。为了降低计算复杂度，本文依据k-最近邻原则（k-Nearest Neighbor，KNN）建立滑动窗口，获得k-近邻剖面子序列，其定义如下：

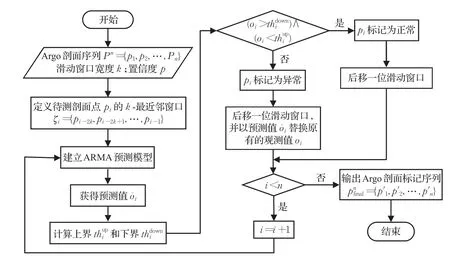
图1 Argo剖面时间序列异常检测算法流程图

定义1（k-近邻剖面子序列）给定Argo剖面时间序列PN={p1,p2,…,pn}和序列中待测剖面点 pi(i＜n)，pi的k近邻剖面点序列为一个连续的长度为2k的剖面子序列，可表示为ζi={pi-2k,pi-2k+1,…,pi-1}。

滑动窗口宽度k决定了预测模型的输入参数量，k越大，计算复杂度会相应的增加。而国际Argo计划希望获取到的测量精度分别为海水温度0.005 C和盐度0.01（PSU/实用盐标）[1]，因此，在满足精度要求的情况下，可以适当调节滑动窗口宽度，从而可以降低算法的计算复杂度。

当通过滑动窗口获得待测剖面点的k-近邻剖面点序列后，下一步便是通过剖面子序列获得待测剖面点的预测值。本文采用可以有效地对时间序列进行预测的自回归移动平均模型（ARMA）。ARMA模型是针对平稳的时间序列的预测模型，而在实际的海洋环境中，可能由于环境影响或者传感器信号的扰动，所获得的Argo剖面数据可能是非平稳的，因此为了保证预测精度，在生成ARMA模型前需要判断Argo剖面时间子序列进行是否是平稳时间序列。若不符合，需进行差分计算转换为平稳时间序列，再建立ARMA模型。

本文依据最小二乘法（Least Squares，LS）原理估计模型系数，并依据最小信息准则[14]（Akaike Information Criterion，AIC）确定模型阶数。参数选择通常选用的是AIC量最小的参数。AIC可以表示为：

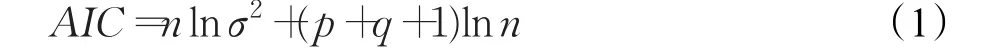
其中，n为样本大小，σ2为拟和残差的平方和。

某个待测剖面点pi的k-近邻剖面子序列为ζi={pi-2k,pi-2k+1,…,pi-1}，在此为了方便描述，记作SM={p1,p2,…,pm}，(m=2k)，其剖面观测值序列为OM={o1,o2,…,om}，(1≤i≤m)，则具体建模方法描述如下：

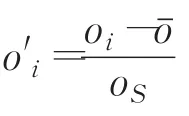
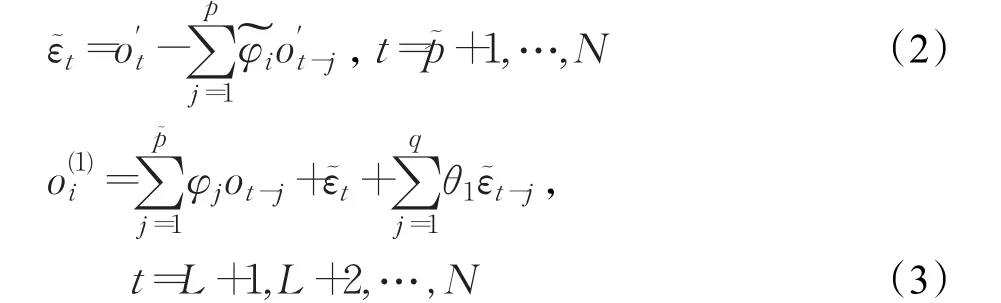
（3）确定剖面预测模型参数的最小二乘估计。对目标函数Q(φ,θ)进行极小化，得到参数的最小二乘估计其中目标函数 Q(φ,θ)表示为：最小二乘估计方法定义如下：

则将目标函数Q(φ,θ)进行改写得到：

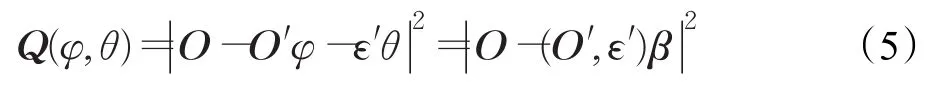
极小化目标函数Q(φ,θ)得到参数的最小二乘估计，依据方程组 (O′,ε′)T[O-(O′,ε′)β]=0 决定，得到解为：

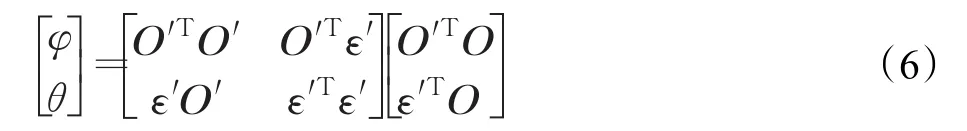
剖面残差序列的方差的最小二乘估计为：

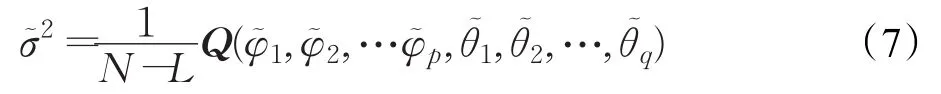
（5）获得剖面预测值。利用线性最小方差方法获取剖面预测值，表示为：

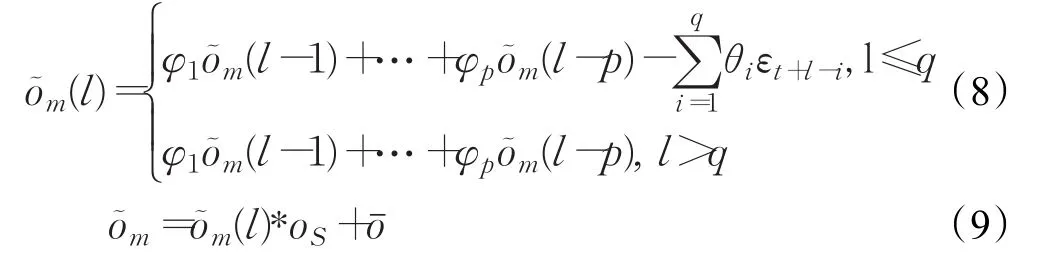
及以前的剖面观测值通过ARMA模型获得的剖面预测值，φi(i=1,2,…p)为自回归参数，θj(j=1,2,…q)为移动平均参数，m为经过反标准化过程后获得的实际剖面预测值。

2.2 异常数据识别与处理

对滑动窗口内的剖面子序列的观测数据进行预测后，需要利用置信区间（Confidence Interval，CI）来判定下一时刻的剖面点观测值是否为异常，置信区间是依据中心极限定理（Central Limit Theorem，CLT）来确定的，其计算如下：

对于给定的Argo剖面时间序列PN，若待测剖面点pi(i＜n)的剖面观测值oi没有在阈值范围内，则待测剖面点 pi被判定为异常剖面点，否则为正常剖面点。为了能够更好地表示出剖面数据是否异常，用Argo剖面标记序列来进行表示，其定义如下：

定义2（Argo剖面标记序列）完成异常检测后，对PN中的每一个点增加一个属性 flag，来标记检测结果。此时，所获得的Argo剖面标记序列可表示为，其中，当检测结果正常，令 flag=1，否则令 flag=0。

当某一待测剖面点 pi经过异常检测后，需要向后移动滑动窗口进行下一个点的检测。为了提高检测的精度，在本文算法采用异常检测缓解策略[17]（Anomaly Detection and Mitigation Strategy）。

当待测剖面点pi经过检测后，判定为正常剖面点，则直接后移一位滑动窗口，更新k-最近邻窗口ζi+1，进行下一个点的检测；若判定为异常剖面点，更新滑动窗口后，需要使用预测值i替换原有的观测值oi，获得新的k-最近邻窗口ζi+1，再进行下一个点的异常检测。图2所示为异常检测缓解策略示意图。

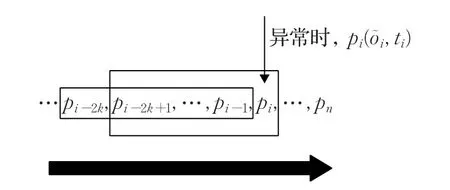
图2 异常检测缓解策略示意图

3 实验结果与分析

为了验证本文算法的效果，本章从预测精度和异常检测效果两个方面对本文所提算法进行实验验证，并与同类经典算法进行对比，分析其优劣性。

实验采用从中国Argo实时资料中心（http：//www.argo.org.cn/）获取的2016年全球Argo浮标剖面数据进行实验，实验数据以.dat文件表示，在Argo剖面文件中包括浮标号、数据采集的经纬度、采集时间等基本信息和压强、温度、盐度属性信息，少数还包括叶绿素浓度、溶解氧等信息。本文的实验环境：CPU为Intel Core i3，2.3 GHz，4 GB内存，操作系统为Windows 7，开发工具为MyEclipse2016，编程语言为Java。

3.1 数据预处理

原始的Argo剖面文件中除了包含多个主要的数据属性外，还包含了大量的与剖面数据异常检测无关的冗余数据，因此无法直接检测原始Argo剖面文件，需要对于数据进行预处理，提取出所需要的属性。而且Argo浮标所观测到的剖面数据具有明显的地域性特点，温度、盐度等数据的变化在不同的经纬度下呈现不同的变化趋势[15-16]，因此不能将所有的数据进行统一的处理，需根据经纬度网格进行划分，再进行数据异常检测。本文算法将Argo剖面数据按照经纬度网格3°×3°进行划分，再选取某一网格中的数据进行实验验证。

本文实验采用盐度属性进行验证，如图3所示，为经纬度为15°N～18°N，138°W～141°W范围内的盐度剖面数据曲线，共有2 011个剖面点。从图3可知，盐度剖面具有周期性，数据整体平稳，但是也存在一些明显的可疑点。

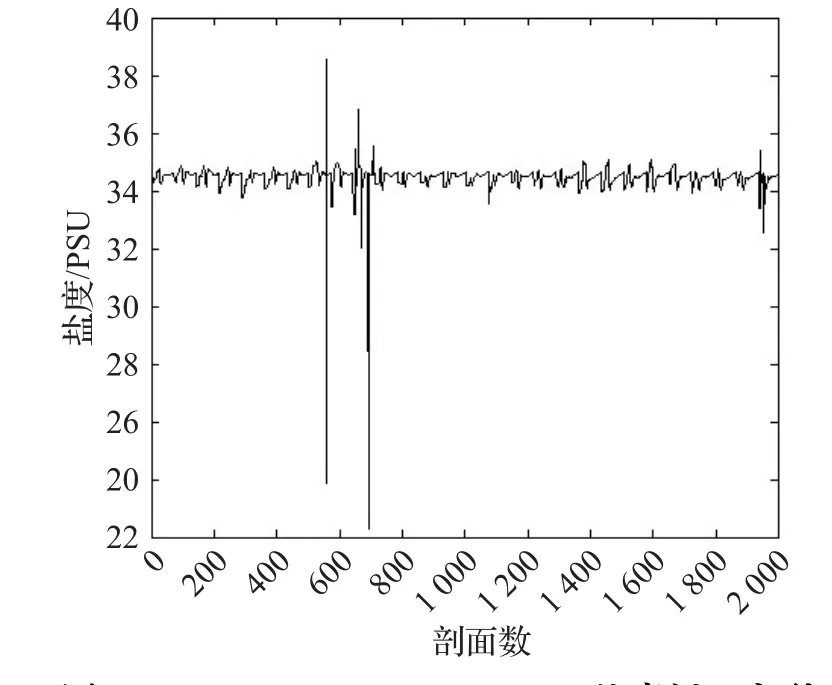
图3 15°N～18°N，138°W～141°W盐度剖面序列

3.2 预测结果

在本文算法中，预测剖面数据是核心步骤，因此，为了检测预测效果，本实验采用均方根误差（Root Mean Square Error，RMSE）和相对均方根误差（Relative Root Mean Square Error，RRMSE）来对于预测结果进行量化评估。

文献[17]中表明LN（Single-Layer Linear Network Predictor，单层线性网络预测模型）预测模型可以获得理想的预测效果，因此在表1中对比了在滑动窗口宽度k=8，k=10和k=12的条件下本文预测模型和LN预测模型的盐度剖面预测误差。从表1可以看出，本文预测模型的RMSE和RRMSE均小于LN预测模型，在本算法中具有较高的精确度，可获得更好的预测效果。

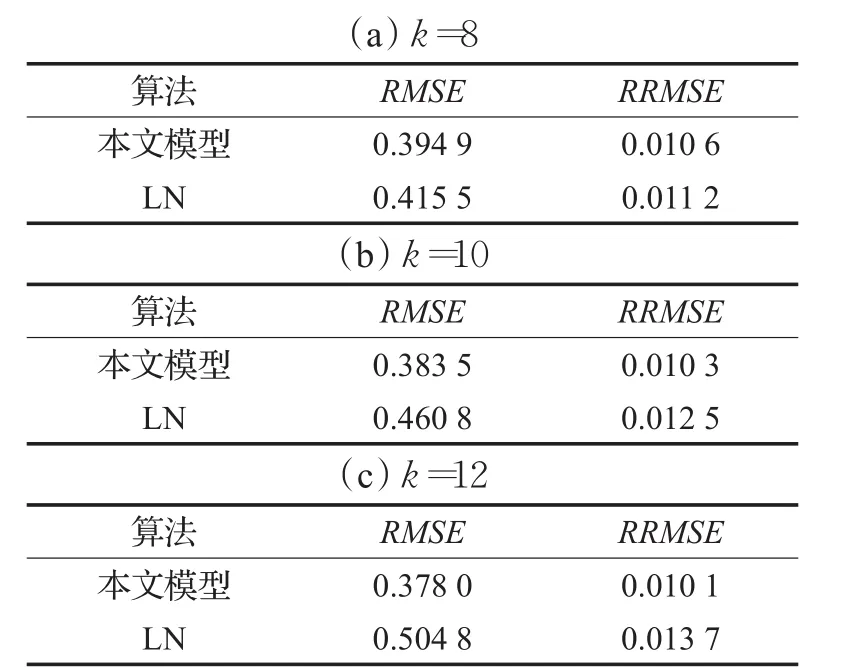
表1 不同滑动窗口宽度下盐度剖面预测误差

表2所示的是本文预测模型在不同的滑动窗口宽度k下的盐度剖面预测误差。从表2可以看出，随着滑动窗口宽度k的不断增大，RMSE和RRMSE不断地减小，因为随着输入的预测参数的增加，预测结果会越准确。

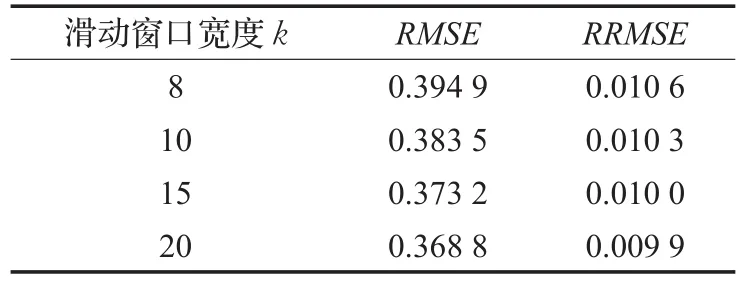
表2 不同滑动窗口宽度的盐度剖面预测误差

图4所示为盐度剖面序列的预测结果，从图5可以看出，预测数据大都与原始观测数据十分接近，只有部分数据与观测数据有较大的偏差，说明本预测模型的预测精度较高，可以有效地应用于Argo时间序列的异常检测中。

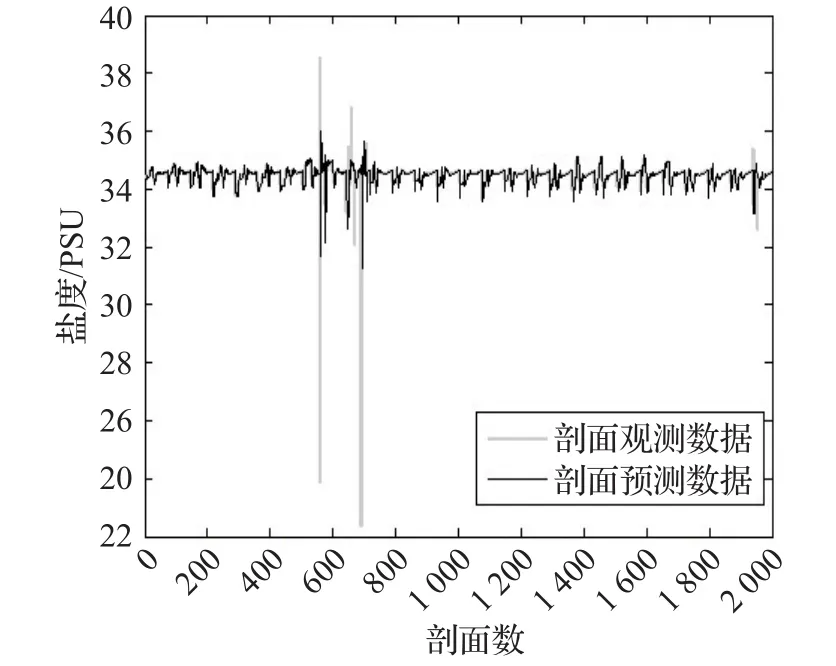
图4 盐度剖面序列的预测结果

3.3 异常检测结果

从上节可以看出，本文算法采用的预测模型，可以获得较好地预测结果，因此，在此预测基础上，可以实现对于盐度剖面序列的异常检测。滑动窗口宽度k=10，置信度p=95%条件下的异常检测结果，如图5所示。

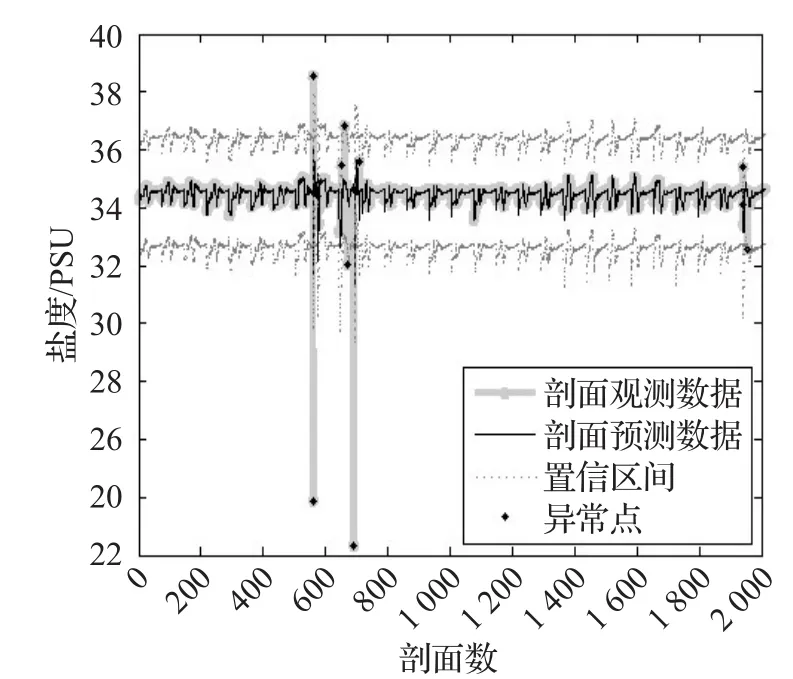
图5 k=10，p=95%条件下的异常检测结果

不同的滑动窗口宽度和置信区间下异常检测的结果可能是不同的。为了能够有效的评价本算法，在此将异常检测结果分为4类，如表3所示。其中，TN和TP是希望出现的结果，而FN和FP是判定出现错误所出现的结果。

表3 检测结果分类

不同参数下的异常检测结果如表4所示。当选择滑动窗口宽度k=10，置信度 p=95%条件下，本文的异常检测算法可以正确检测出异常剖面点10个（TP=10），正常剖面点被正确判定出来的剖面点有1 994个（TN=1 994），但是有2个正常剖面点被错误的判定为异常剖面点（FP=2），最后，还有5个异常剖面点没有被检测出（FN=5）。

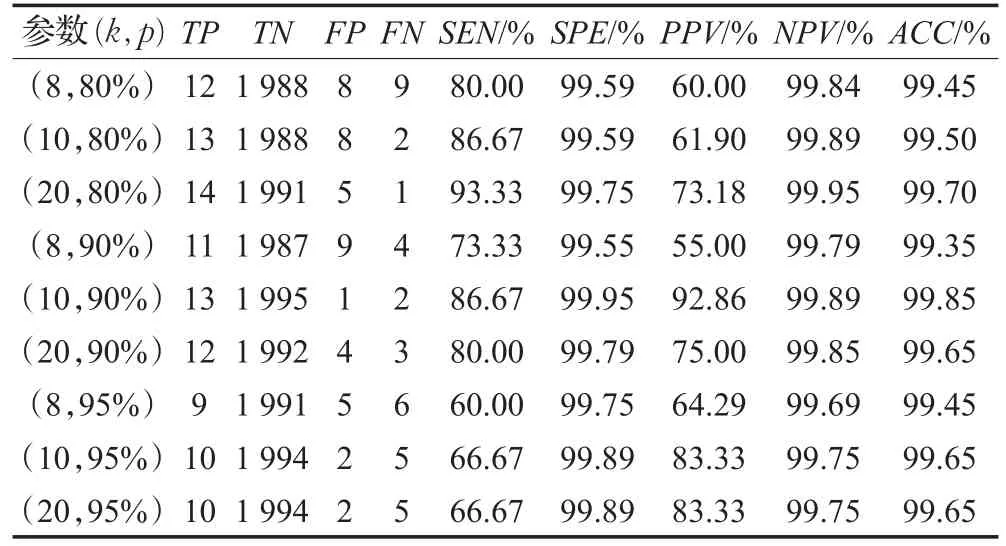
表4 不同参数对异常检测的结果对比

通过对比表4的评估结果可以看出，本文的异常检测算法的特异度很高，一直保持在99%以上，说明本算法可以很好地检测出正常剖面点为正常。但是，当置信度 p≥95%时，敏感度只有60%左右，说明当置信区间范围设置过大时，能够真正判断出异常剖面点的效果不是很好，而当置信度设置在 p∈[80%，90%]范围内时，敏感度可以维持在80%以上，而且随着滑动窗口宽度k的增加，敏感度呈上升趋势。此外，本文算法的精确度一直维持在99%以上，说明本文算法可以准确地判断出正常剖面点或者异常剖面点，其他的指标也维持较高的水平。当滑动窗口宽度k∈[10,20]，置信度 p∈[80%，90%]时，敏感度可以达到85%以上，并且特异度可以维持在99%，准确度在99%以上，说明本文的异常检测算法具有较高的可靠性。

为了能够更好地评估本文的异常检测算法，将本文方法与其他的异常检测方法在同一张“受试者工作特征”[18]（Receiver Operating Characteristic，ROC）曲线上。在ROC曲线中，横坐标是“假正比率”（False Positive Rate，FPR），纵坐标是“真正比率”（True Positive Rate，TPR），两者的公式为：

在进行算法比较时，当一个算法的ROC曲线被另一个算法的ROC曲线完全“包住”，则可说明后者的性能优于前者。从公式（12）可以看出，FPR就是“1-特异度”，而TPR就是“敏感度”。在异常检测中，理想的是获得高TPR，低FPR，意味着曲线越接近坐标轴的左上角，算法的精确度越高，性能越好。

图6所示的是本文的异常检测算法与经典的温盐关系模型的异常检测方法[4]、基于“LN”预测模型的异常检测方法[6]和k-近邻方法[19]的ROC曲线对比图。图6表明，本文方法的异常检测效果优于其他异常检测方法。温盐关系模型方法采用的是最小二乘法拟合历史温盐数据获得上下界来实现异常检测，但是由于该模型的精确度不高导致异常检测的效果是最不理想的。k-近邻方法的效果虽然优于温盐关系模型方法，但是相较于其他两种方法，检测效果一般。基于“LN”预测的方法与本文方法检测效果较为接近，但是由于该方法的选取的预测模型应用于Argo剖面数据集中，预测误差较大，所以其检测效果相较于本文方法略逊一筹。而本文方法的ROC曲线始终位于最上方，完全“包住”了其他3种方法，所以检测效果最好，准确性高。

图6 不同方法的ROC曲线

4 结束语

本文针对Argo剖面数据，提出了一种基于滑动窗口和ARMA的Argo剖面数据异常检测算法，本文算法利用滑动窗口划分剖面序列，结合ARMA模型获取剖面预测数据，并采用中心界限定理计算出动态阈值来实现异常检测的方法。通过真实的全球Argo浮标剖面数据进行实验，验证了本文方法的异常检测准确性和可靠性高，能够有效地提高Argo浮标剖面数据的数据质量，具有较高的实用性。在此基础上，下一步将研究多属性下对于Argo剖面的异常检测，为其他领域的研究提供更高质量的Argo剖面数据集。