融合用户动态标签和信任关系的协同过滤算法

吴鸿玲，程耕国

1.武汉科技大学 信息科学与工程学院，武汉 430081

2.武汉科技大学 冶金自动化与检测技术教育部工程研究中心，武汉 430081

1 引言

随着电子商务的快速发展，可提供的商品信息资源也日渐丰富，传统的推荐算法[1]通过分析用户购买和评分的历史记录来进行预测和推荐。然而协同过滤推荐算法面临着一些挑战[2]，如数据稀疏、评分数据不均衡、冷启动等问题，使得系统难以向新用户准确地推荐商品。

为了有效地获取用户和商品的相关信息，并快速准确地为用户推荐感兴趣的商品，近年来，基于社会化属性的推荐算法得到了广泛关注，有研究将信任关系引入到推荐系统的算法中，提出基于用户信任关系的过滤推荐模型。例如，文献[3]描述了一种基于用户信任关系的协同过滤算法原理，它依据可靠性测试来建立邻居用户，进而根据邻居用户进行推荐。与“基于相似度评价的协同过滤算法”模型相比，“信任关系”模型[4]在参考用户选取方面有所不同，它主要基于核心信任用户的信息来向用户推荐商品。文献[5]中提出朋友关系为推荐系统中的重要信息之一，通过计算朋友间相似度，修正张量分解以建立推荐模型。文献[6]提出一种基于共同用户和相似标签的协同过滤算法，它通过把用户个人标签信息加入到最近邻协同过滤方法中以改善热门用户对推荐的影响。文献[7]提出FTCF算法，它通过关系传播机制寻找关系网络中与目标用户兴趣爱好相似的用户，并找到符合目标用户需要的商品，利用TF-IDF思想，从用户历史标签记录中挖掘该用户的兴趣爱好，最后将两者进行结合来解决数据稀疏问题。文献[8]提出一种IBCF算法，它通过在项目间引入信任关系来计算项目相似度，在一定程度上提高了推荐精准度和覆盖率。文献[9]提出SemPMF算法，它使用非监督方式生成语义项特征，并将其与用户项目偏好矩阵结合起来进行推荐，提高了推荐质量。

然而，这些推荐系统存在以下不足：（1）覆盖率指标与推荐精度存在互斥问题，采用的社会网络信任取值为二进制形式，即0-1表示方式，导致推荐精度下降；（2）二进制0-1的表示方式会使用户间的信息不对称，因此信任值的合理计算对于提高算法性能至关重要；（3）以朋友关系式用户或共同关注式用户来计算信任值，使得信任关系中的用户变窄，不具有普适性；（4）虽然在一定程度上提高了推荐的准确度，然而其推荐历时较长。

为解决上述问题，提出一种融合用户动态标签和用户信任关系的矩阵概率分解模型（Probability Matrix Factorization Model based on user dynamic Tags and user Trust relationships，TTPMFM）。

2 用户与物品间的偏好标签矩阵

2.1 用户与物品间的动态标签关系

用户通过对项目添加注解来设置标签，且所设置的标签具有一定的社会属性[10]，能引导和帮助用户浏览和组织资源。本文采用三元组的形式在标签集、用户集和项目集之间建立动态联系，具体如图1所示。

其中，用户集涵盖了系统中的所有用户。标签集包括了系统使用的所有标签，每个标签可用词语来表示，如“数据挖掘”。项目集囊括了模型中的所有项目资源，并且每个项目资源有唯一编号。

2.2 用户动态标签偏好评分矩阵

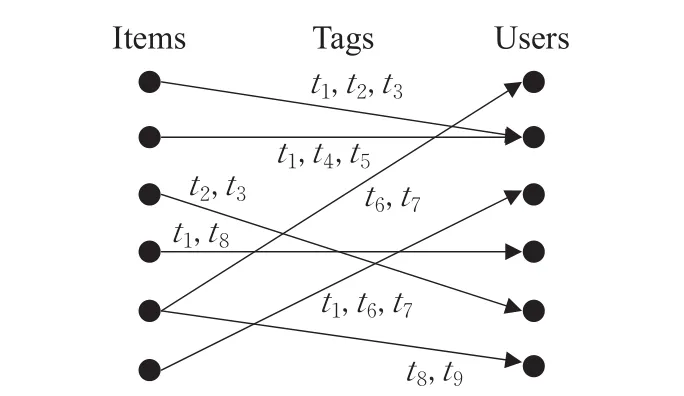
图1 用户标签动态关系图

用户在访问项目资源时，通常表现出两类行为：（1）对标签进行查找、新增和关注；（2）与资源进行交互，例如浏览、点击和收藏等。这两类行为可以充分表现出用户实时的偏好行为。通过计算这两类行为的相关特征，并将其作为算法预测的权重，可以更好地向用户推荐资源。

标签的质量可用Sigmoid函数[11]进行计算，从而获得相关特征的权重。假定项目i与对应标签t之间的权重值为w(i,t)，则可通过式（1）来计算w(i,t)。

其中，m是推荐标签的质量，且满足关系m=TF×IDF，其中TF为词频参数，指的是文档d中词条t的出现次数，IDF为文档的逆频文件频率，指的是文档频率与词条t频率之间存在的反比关系。

为了对系统用户与资源的交互过程进行用户偏好标签的预测推导，将用户的偏好用评分来表达。这种方法也称项目资源评级（Item-Rating，IR）。该方法充分考虑了相关特征权重对标签偏好预测推导过程的影响。

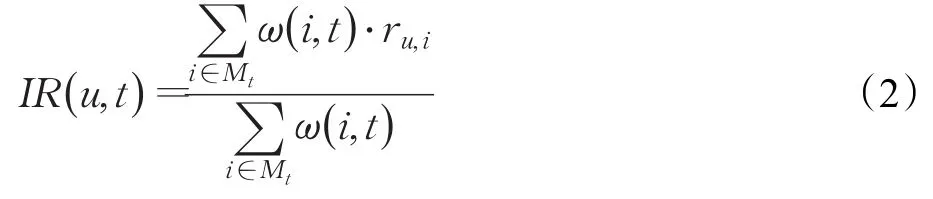
式中，变量ru,i表示用户u对项目资源i的评价分数，变量ω(i ,t)是项目资源i与标签t之间的权重，变量Mt是包含显式标签t的所有项目资源集。

然而式（2）未考虑用户未评价过的项目资源，例如，当用户对某个项目资源执行收藏、关注等操作时，表明此类项目资源是用户偏好的。为了展示隐式标签对项目资源预测推导的作用，采用公式（3）对用户偏好进一步预测：

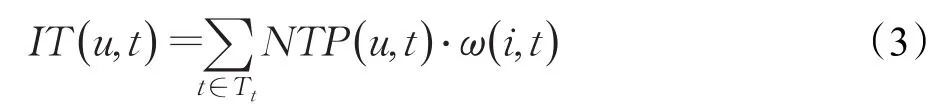
综合考虑显隐式标签，即将式（2）和式（3）结合，则用户与物品间的偏好标签矩阵为：

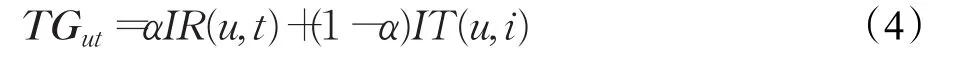
式中，TGut为融合显式标签与隐式标签后的用户偏好标签矩阵，且使用α（0≤α≤1）调节因子来为物品显式标签与物品隐式标签设置权重。

3 用户信任关系矩阵

基于图的概念引出用户信任关系图，并分析用户信任关系的建立过程。同时，在用户信任关系的基础上，建立基于用户信任关系图的反馈机制。

3.1 用户信任关系分析

从人类社会关系的推荐角度来看，人们通常倾向于信任来自其熟人所推荐的信息。在电子商务推荐系统中，所有用户都可以通过图来建立用户间的信任关系，如图2的A所示，实线代表用户间的直接信任关系（N1信任N2，N2信任N3）。通过N2与N3之间的信任关系，用户N1间接地信任N3。如果N2与N3之间没有信任关系，那么不可能在N1和N3之间建立信任关系，如图2的B所示。下面给出与信任相关的一些定义。

定义1（直接信任）通过定义一个三元组＜i,j,DTi,j＞来表示直接信任，其中三元组代表从节点i指向节点 j的有向边，DTi,j代表节点i到节点 j的直接信任值。

定义2（间接信任）通过定义一个三元组＜i,j,IDTi,j＞来表示间接信任，其中节点i通过有限跳H(H＞1,H∈N)到达节点 j，IDTi,j代表节点i到节点 j的间接信任值。

定义3（直接信任偏好准则）对于信任图中的任何一个节点i，它的直接信任节点比间接信任节点更加可信。例如图2的A中DTN1N2比IDTN1N3可信度更高，即DTN1N2＞IDTN1N3。

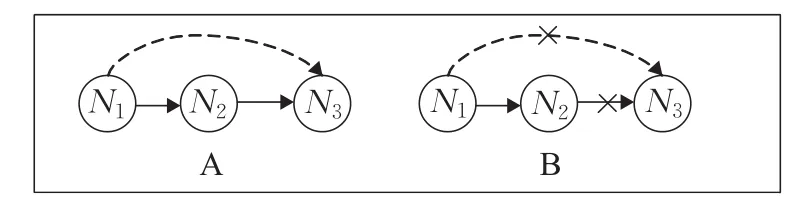
图2 人类社会中的信任过程

3.2 用户信任关系的建立过程

用户信任关系的主要因素是用户偏好相似性和用户的影响力。为了在用户间建立信任值，需设置阈值θ来获取用户之间的相似度，如式（5）：

用户间的信任关系具有转移性和方向性等非对称特性，通过使用这些非对称的信任关系信息，可以有效缓解用户评分矩阵的数据稀疏问题。为了测量用户间的影响力，使用Jaccard距离[12]来衡量用户的非对称关系。的计算公式如式（6）：

用户间的信任值TRu,v主要由用户间相似度和用户间影响力组成，通过分配不同的权值计算TRu,v，如式（7）：

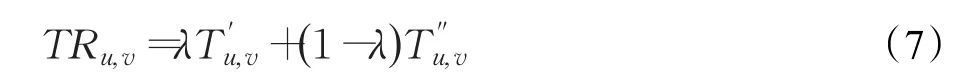
3.3 基于用户关系图的信任反馈机制

定义4（信任查询机制）根据输入的查询深度Level，查询与活跃用户节点Ni有关联的直接信任值和间接信任值，直到查询深度大于Level为止。将所有查询到的直接信任用户与间接信任用户存放到信任用户TNLl列表中。

定义5（反馈机制）基于信任值TRu,v（包括直接信任值和间接信任值）和项目评分值Rvi，根据公式（8）计算项目i的预测评分PRV(i)。如果PRV(i)与用户的实际评分Rui相差不大，即满足式（9），则将信任用户列表TNLl中的top-N反馈给用户u；如果相差太大，则更改阈值θ，直到项目i的预测评分PRV(i)与用户的实际评分Rui相差不大为止。其中，Rvi为信任用户对项目的评分值，Rui为活跃用户对项目i的评分值。

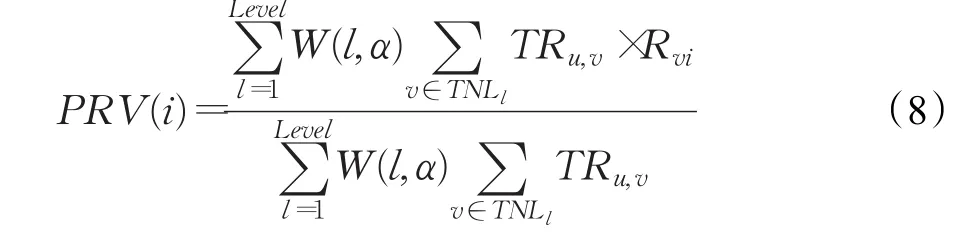
式中，Level代表距离节点Ni的距离；W(l,α)代表信任值的加权因子函数，如式（10）所示；TNLl代表活跃用户U直接信任和间接信任的用户列表。

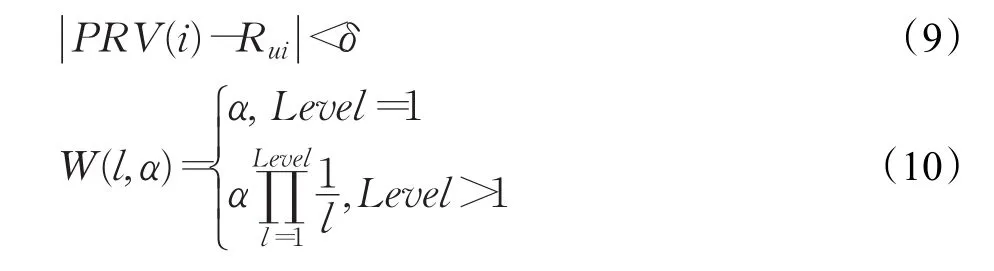
式中，α代表信任值初始衰减因子。

基于前文所述的用户信任关系，提出一种基于用户信任关系图的反馈机制，如图3所示。

图3 基于信任的用户反馈模型

图3 中，边缘代表不同节点之间的信任关系。当请求用户U0的推荐信息时，首先，该节点根据信任查询机制向其直接信任节点（U1和U4）发送信任查询信息，这些节点也同样向其受信任的节点发送信任查询信息，直到信任查询过程结束；然后，基于反馈机制选择信任值高的前N个用户，并反馈其所有产品的信任值。通过此信任反馈模型，可以得到用户U0的受信任节点（包括直接信任节点和间接信任节点）所推荐项目的综合评分。

4 融合用户动态标签与信任关系的概率矩阵分解模型

在矩阵概率分解过程中，主要基于潜在用户特征与信任间存在的内部关联来实现信任矩阵的预测和计算。

文献[13]中所使用的矩阵概率分解模型（Probability Matrix Factorization Model，PMFM）如图4所示，该矩阵分解模型具有线性概率特征，它将用户对项目的评价问题转换为概率问题，其中σν和σμ为用户和物品的隐式特征向量，σR为用户评分数据。然而，该模型未考虑到参与评分用户的信任级别以及用户与物品标签间的动态联系。实际评分过程中不同用户具有不同的定位和角色，过于均值化的评分概率预测不利于体现重点用户的评分意见，不能获得较为合理的决策结果。同时，用户对物品标签的偏好是动态的，在实际推荐系统中，需要获取用户与物品标签的偏好交互行为，这样才能更好地向用户推荐商品。

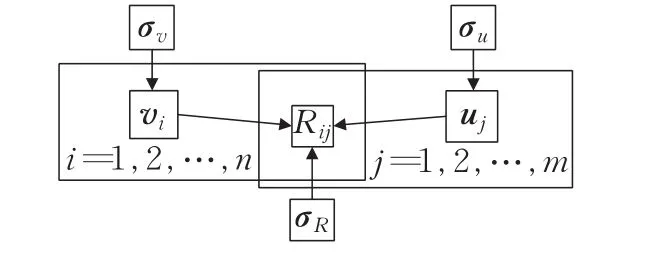
图4 PMFM模型

为解决上述问题，融合信任关系和动态标签，设计如图5所示TTPMFM模型。在TTPMFM模型中，评分矩阵为n行m列，其中，第 j行对应的潜在特征为uj，第i列对应的潜在特征为vi。，Nui为具有相似偏好标签的用户集合，Nvi为用户u所信任的用户集合，tg(u1,t)为用户u1与物品标签t之间的关联程度，tr(v1,u)为用户v1与用户u之间的信任程度，且tg(u1,t)与tr(v1,u)分别来源于用户偏好标签矩阵和用户信任关系矩阵。

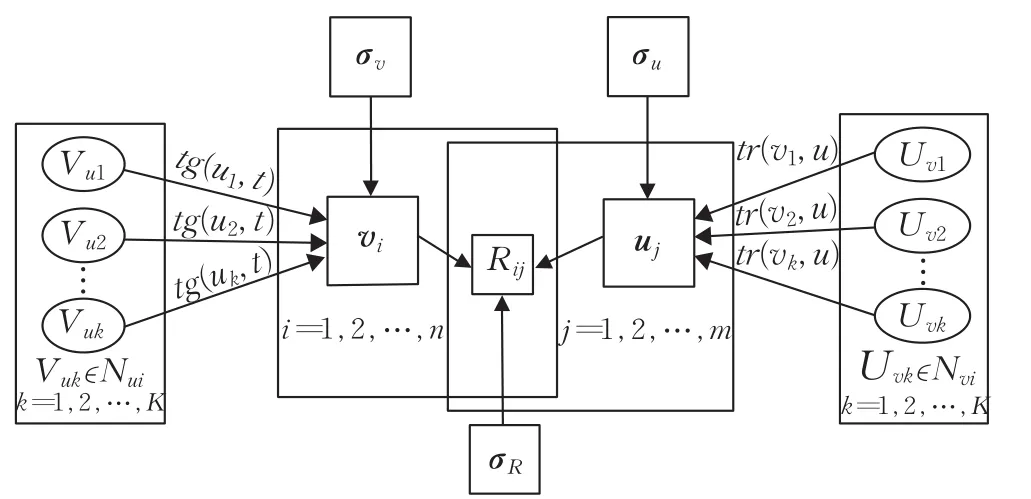
图5 TTPMFM模型

在进行模型求解过程中，uj和vi两个潜在特征均服从高斯特征分布，以来表示，融合用户动态偏好标签矩阵和用户信任关系矩阵后，用户动态偏好矩阵与物品潜在特征的联合概率分布为：

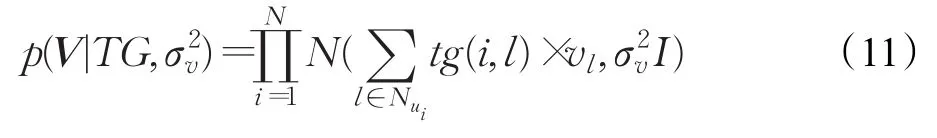
同理，用户信任关系矩阵与用户潜在特征的联合概率分布为：

并且在TTPMFM模型中，U和V相互独立，评分矩阵R的条件概率为：

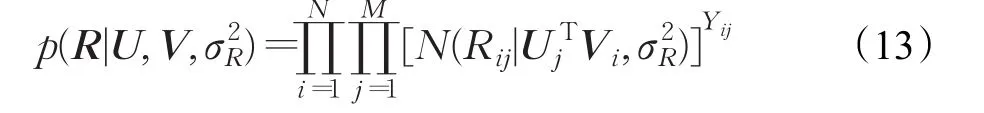
结合公式（11）、（12）和（13），通过贝叶斯推理可以得到用户和物品潜在特征的后验概率分布为：

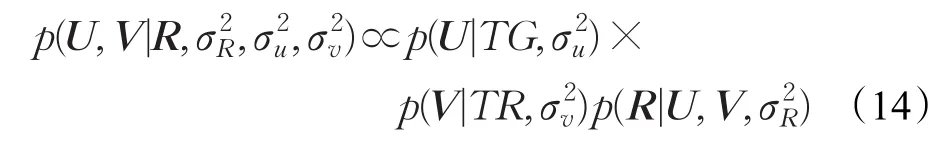
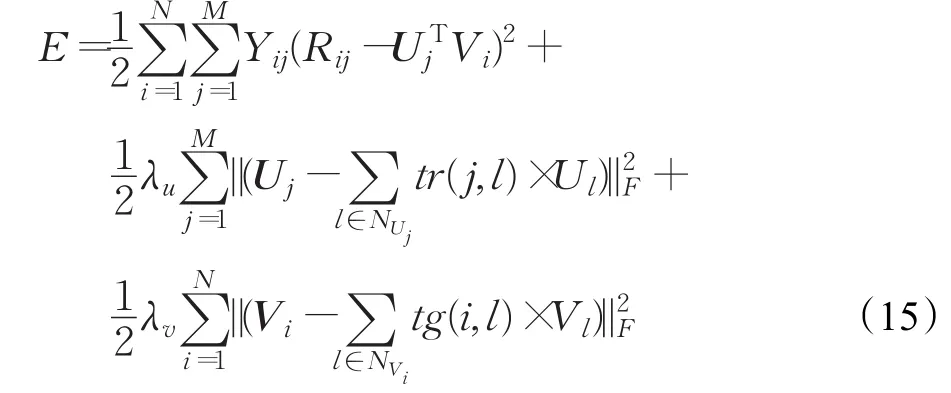
利用梯度下降法来对目标函数进行求解，对每个用户Uj和每件物品Vi分别求偏导，如式（16）和式（17）：

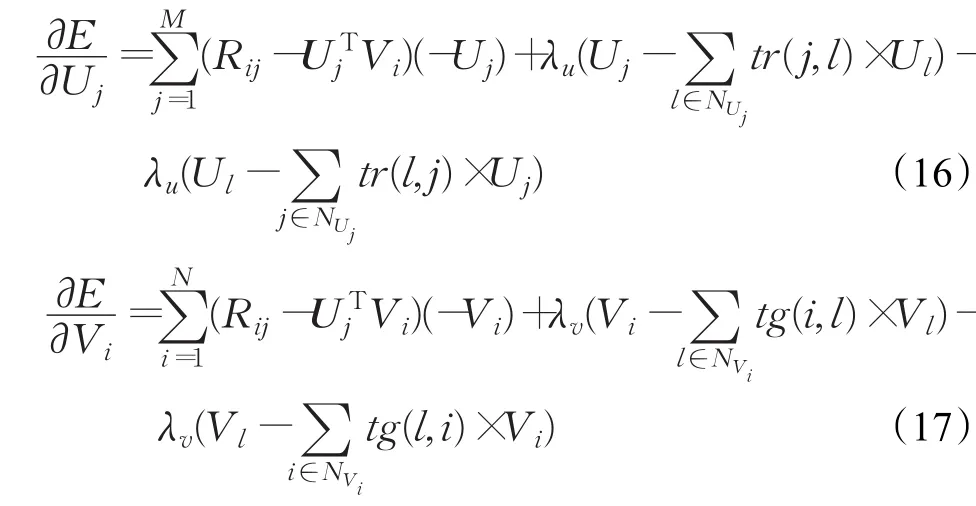
综上所述，TTPMFM模型的求解过程描述如下。

输入：用户与物品之间的动态偏好标签矩阵TGut，用户信任关系矩阵TRu,v，用户项目的评分矩阵R，近邻参数k。

输出：预测目标用户对未评分项目的评分值。

求解步骤：

（1）根据数据集计算用户-项目评分矩阵。

（2）根据公式（4）计算用户-项目的动态偏好标签矩阵。

（3）根据公式（5）计算目标用户与其他用户之间的信任关系。

（4）根据步骤（2）和（3）得到的矩阵，利用K-NN算法[14]获得目标用户u的K个用户-项目偏好标签集合，以及K个与目标用户信任值极高的近邻用户集合。

（5）设置迭代初始步数i=1，将步骤（4）得到的集合带入公式（15）。

（6）根据梯度下降法原理，计算目标函数的下降可行方向d(i)，并依据公式（15）中的约束条件来计算下降方向的步长[0，λmax]。

（7）根据步骤（6）所获得的下降方向以及步长范围，利用0.618法[15]计算最优步长λi。

（8）遍历步骤（4）所得到集合的每个数据。

（9）获得公式（16）、（17）的最优解，最终得到目标用户u所有参数。

（10）对步骤（9）得到的目标用户参数进行矢量相乘，即获得目标用户对待评物品的预测值。

5 实验结果及分析

为了进一步提高计算速度，实验平台使用VMware Workstation9.0虚拟软件将1台TS250联想塔式服务器（Intel至强E3-1200 v6处理器，8 GB内存）虚拟成8台虚拟主机，1台惠普PAVILION 14-AL125TX作为Master，在Ubuntu 12.0.4系统上部署计算机集群，集群中包括8个DataNode和1个TaskTracker。

5.1 实验数据

在MovieLens数据集以及Jester-Data数据集上对所提模型进行验证。在基于包含用户对电影的评分信息、用户间的评价信息、用户的人口特征统计等类型信息的数据集上预测模型做出的用户评分。使用Python爬虫技术随机从淘票票站点抓取了943个用户对1 682部电影的评分数据，共计100 000条评分信息，其中每组用户至少对10组标签进行了评分，原评分区间为1～10之间的整数，为了便于计算，将其归一化为0～1之间的区间。评分值越高，则表明用户对电影的喜好程度越高。即在MovieLens测试集中，共有943组用户，1 682组电影，100 000条标签评分信息，其中每组用户至少对10组标签进行了评分。考虑到Jester-Data数据集过于稠密，因此该数据集（用Python技术随机在百度新闻站点上抓取数据）选取1 743组用户，这些用户对121组新闻进行了评价，包含18 924组用户标签评分信息，且每组用户至少包含一组用户标签评分信息。这两个数据集的相关属性如表1所示。

为了使实验结果不失一般性，采用5-fold交叉验证方法，将数据集分为测试集和训练集，比例为1∶4，且这两个集合互补，能涵盖整个数据集。

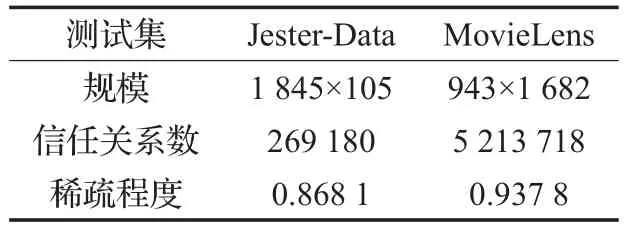
表1 数据集相关属性

5.2 评价指标

（1）平均绝对误差指标MAE：

其中，pi表示用户的预测评分，ri表示用户的实际评分，N表示评分条数。平均绝对误差值越小，推荐系统的推荐精度越高。

（2）平均准确率指标Precision和平均召回率指标Recall：

其中，Ru为模型根据训练集用户的行为给用户做出的Top-N推荐集，Tu为用户对测试集所做出的正面评分集，N为测试用户的数目。平均准确率和平均召回率的值越大，所预测出的项目越接近目标用户，表现出的推荐效果越好。

5.3 实验结果分析

（1）阈值对数据集的影响

在Jester-Data测试集和MovieLens测试集上设置不同的阈值，并设定用户近邻参数值为8，测试这两个数据集的平均绝对误差。实验结果如图6所示。

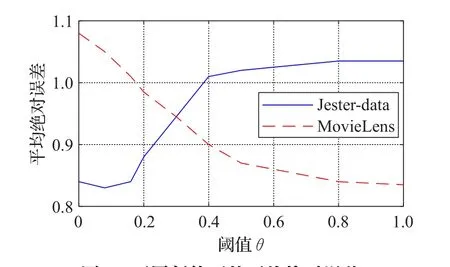
图6 不同阈值下的平均绝对误差

从图6可以看出，随着阈值θ不断增大，MovieLens测试集的平均绝对误差呈下降趋势（先迅速下降，后趋于平稳）。而对于Jester-data测试集，其平均绝对误差先缓慢下降，再逐渐增加，最后趋于平稳。这是由于Jesterdata测试集的规模要小于MovieLens测试集的规模。当阈值θ较小时，由于MovieLens测试集的规模大，当前用户的信任关系用户较多，计算用户相似性的时间复杂度和空间复杂度较大，因此无法快速准确地为当前用户生成推荐；而Jester-data测试集的规模小，通过公式（5）、（6）、（7）可以计算出较高信任值的用户，因此可以为当前用户准确地生成推荐信息。当阈值θ较大时，由于Jester-data测试集的规模小，当前用户的信任关系用户较少，导致相似性用户较少，无法计算出较高信任值的用户，因此缺少足够的评分数据来进行预测推荐；而MovieLens测试集的规模大，可以计算出较高信任值用户，因此可以得到足够的评分数据来进行预测推荐。

由图6可知，对于Jester-data数据集，阈值θ设定为0.1时，推荐性能最佳；对于MovieLens数据集，阈值θ设定为1时，推荐性能最佳。因此，针对不同的数据集，需要选取合适的阈值θ才能获取准确的推荐信息。

（2）与其他算法性能的比较

为了验证所提算法的性能，以MAE、Precision以及Recall为评估指标，选取FTCF[16]、IBCF[17]以及SemPMF[18]3种经典的协同过滤算法，在不同近邻参数K下进行训练和测试。如图7为4种算法在不同近邻参数K下的平均绝对误差、准确率及召回率的对比。

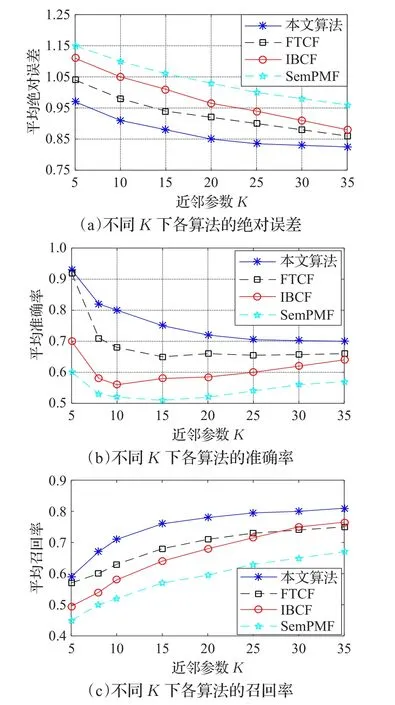
图7 不同近邻参数K的实验结果

从图7的实验结果可以看出，与FTCF、IBCF以及SemPMF算法相比，本文算法在不同近邻参数K的环境下，均可获得良好的性能。这是由于本算法在推荐过程中融合了用户的动态偏好标签和信任关系，使得推荐模型能迅速感知用户的喜好并基于用户的社会化属性选择近邻用户，从而向当前用户准确地推荐商品。

6 结束语

针对社交网络的推荐因信任值存在互斥导致的推荐精度下降的问题，提出了一种融合用户动态标签和用户信任关系的矩阵概率分解模型。它在一定程度上缓解了传统的协同过滤算法存在的数据稀疏、用户评分不均等问题，提高了协同过滤推荐算法的性能。实验结果表明，该算法模型在绝对误差均值、准确率与召回率方面获得了不错的效果。目前，有关推荐系统中信任关系的研究主要体现在强关系和弱关系上，而关于非信任关系的研究很少，本文接下来可以针对非信任关系做进一步的研究。