噪声不均条件下的模糊C均值聚类算法及应用

王文慧，杨 庚，葛 炜，刘沛东，钱 晨

1.南京邮电大学 计算机学院 江苏省大数据安全与智能处理重点实验室，南京 210000

2.江苏亨通光电有限公司，江苏 苏州 215200

3.南京邮电大学 光电学院，南京 210000

1 引言

随着科技的进步，光纤通信技术从光通信中脱颖而出，已成为现代通信的主要支柱之一，在现代电信网中起着举足轻重的作用。在光纤光缆的生产过程中，由于生产工艺和环境的影响，会导致表面不同种类的缺陷存在，这将直接影响到产品的寿命。依赖人工进行瑕疵的检测，这种方法劳动强度大，效率低，而且难以适应大规模工厂化的生产需求。同时人工检测法在实际使用中存在很大的局限性。采用计算机视觉技术可以客观、及时、准确地识别光缆表面的瑕疵。随着计算机视觉和数字图像的处理技术在工业的广泛应用，利用计算机技术实现光缆瑕疵的自动检测成为可能。在图像分割技术的发展中，产生了多种分割方法，比如：阈值分割法、区域法生长法、边缘检测法、基于特定理论的分割法等[1]。

在基于特定理论的分割方法中，一些基于聚类的分割方法被提出来。其中使用最广泛的是模糊C均值FCM聚类算法。HE等人[1]充分考虑了像素的空间信息，提出了一种具有空间约束的FCM算法，该算法通过修改目标函数和隶属度函数，提高了算法的抗噪性，取得了较好的效果。Sowmya等人[2]提出了使用FCM算法和神经网络结合的方法对彩色图像进行分割，该方法比单一的FCM算法分割精度高，但是该算法需要大量的训练数据，不适用于实时性的检测。Bai等人[3]提出了一种改进的FCM算法来分割红外船舶图像，通过马尔科夫随机场来细化局部空间约束，较好地克服了噪声不均性。

FCM算法克服了普通聚类算法中硬聚类的缺点，但在分割过程中仍然存在以下缺点：（1）没有考虑图像相邻像素的关系；（2）使用鲁棒性较差的欧式距离衡量像素与聚类中心的差值；（3）初始聚类中心具有随机性，导致每次运行的时间和分割效果差异较大。基于以上原因，该算法对噪声非常敏感。针对以上不足，本文提出了一种结合像素邻域信息并改进欧氏距离的模糊C均值聚类算法。使用该算法，对获取的彩色光缆图像在R、G、B三个维度上进行聚类，实验结果显示能够准确定位光缆的瑕疵区域，并很好地克服了噪声的影响，证明了算法具有很好的鲁棒性。

2 传统模糊C均值聚类分割算法

FCM聚类算法是一种无监督的分类方法，通过对目标函数的迭代优化实现对像素的划分[3]，根据每像素属于不同区域的程度将像素分到某个区域中。由于图像的退化、受外界噪声和其他不确定因素的影响，在分割中很难将像素归属到某个分类器中，而FCM算法将分类器之间的独立性用一种模糊的概念来取代，克服了硬分类方法将像素归属一刀切的不足，在某种程度上能克服不确定因素对像素分类造成的影响[4]。

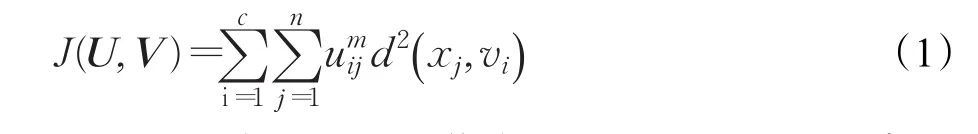
式中，J(U,V)表示区域的像素到聚类中心加权距离的平方和，J(U,V)值的大小反映图像区域的一致性，值越小表示像素是一个区域的可能性越大，聚类效果越好[6]。参数m是隶属度的加权指数，是为了加强像素的特征值属于不同区域的对比度，它决定分类结果的模糊程度，m∈[1,+∞)，其值越大分类越模糊，当m=1时，为硬分类，一般值取m=2。式（1）需要满足如下约束条件：

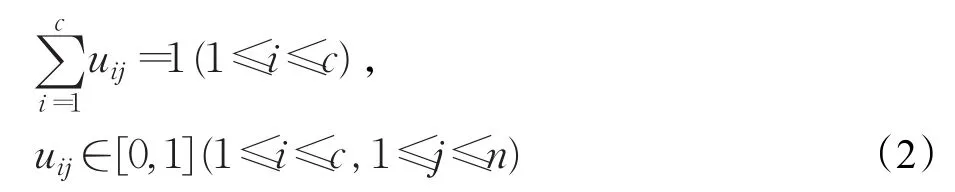
为使J(U,V)取到最小值，该带约束条件的极值问题可通过拉格朗日乘子法解决，相应的迭代算法描述如下：

步骤1初始化。设定聚类类别数C、模糊指数m和迭代的终止条件ξ，并用随机数初始化隶属矩阵U(0)，令迭代次数 k=0[7]。

步骤2计算聚类中心：

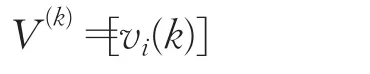
其中：

步骤3计算隶属度矩阵：

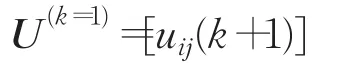
其中：

步骤4如果停止循环迭代，否则令K=K+1，回到步骤2继续循环。

3 改进的模糊C均值聚类算法

3.1 初始聚类中心与聚类数的选取

根据对光缆瑕疵图片的了解，将聚类数目选择为2，即一类为瑕疵，另一类为光缆的正常部分。FCM算法中，聚类中心的选择是随机的，这样可以简化算法的复杂程度，整个算法的工作集中在聚类的迭代上，算法的代码实现更容易。但是，FCM算法的迭代终止条件是相邻两次迭代的聚类中心变化足够小，则认为算法已经收敛。由于算法的每一次迭代都是沿着使目标函数减小的方向进行的，而目标函数可能有多个极值点。随机的初始化可能使聚类中心落在局部极小点附近，使算法收敛到局部极小值[8]。而光缆表面的瑕疵样本和非瑕疵样本数目有可能相差很大，在这种情况下，很容易使目标函数收敛到局部极小值，造成每次分割的效果差别较大，降低了分割的准确率。为解决目标函数中聚类中心初始化的随机性，对彩色光缆原图如图1，在G、R、B三个维度上计算它的直方图，直方图如图2所示。由于已经确定了聚类数目为2，在RGB直方图上选择波峰最大的前两个，它们对应的像素值就是聚类中心。

图1 光缆原图

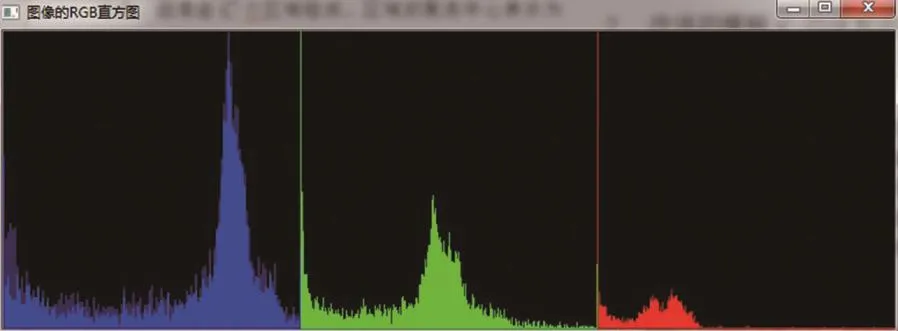
图2 光缆原图对应的RGB直方图

对同一副图片，在精度均为1E-6的情况下，比较了随机初始化聚类中心与根据直方图初始化聚类中心的迭代次数，并在两种初始化方式下多次同一副图像进10次分割，随机初始化的方式中出现2次不理想的分割效果，根据直方图初始化则效果理想且稳定，具体图像见图3。具体数据见表1，v[i][j]代表第i类聚类中心，j分别取0、1、2代表聚类中心在B、G、R三个维度上的值。

通过实验可以看出，根据直方图给聚类中心赋值的方法，可以减少程序处理图像的迭代次数，使其更快地逼近预设的精度。假如在图片像素量大并且要求精度较高的情况下，这样对聚类中心的预处理会大大减少程序运行时间。图3中（a）、（b）图是10次分割中随机初始化聚类中心时出现的分割不理想的情况，（c）图是分割理想的情况，使用直方图初始化时分割效果一直如（c）图，所以随机初始化时分割效果不稳定，而直方图初始化则分割效果稳定。

图3 不同初始化分割效果

表1 初始化聚类中心方式及迭代次数

3.2 改进FCM算法的目标函数

3.2.1考虑图像样本的邻域信息

标准的模糊C均值聚类算法仅仅考虑到像素的灰度信息，没有考虑到像素与像素中间的关系[8]，即像素的空间约束性信息，因此，在分割含有噪声的光缆图像时，会把噪声点或者因光照不均而造成的亮斑或暗斑划分到瑕疵这一类中，使分割效果受噪声影响严重。为了增强算法的抗噪性，结合邻域像素信息，考虑通过滑动窗口（3×3）求出像素的邻域平均值，FCM算法的目标函数相应的变化为：

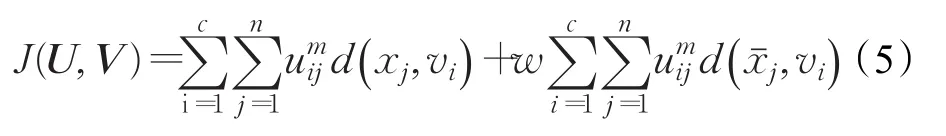
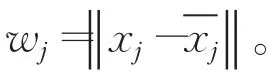
3.2.2 改进欧式距离

对于数据集X={x1,x2,…,xn}，传统方法通过计算欧氏距离

这种度量xj与v的距离的方法叫做欧式距离，这种距离估计方法称为最小二乘法。考虑一个数据集{3，4，4.4，4.7，4.9，5，5.1，5.3，5.6，6，7}，通过式（7）得到该数据集中心为v=5。但是如果在数据集中增加一个噪声点30，那么中心v就会变为7.08，这个数值不在原始数据的范围内，显然这个方法会因为噪声产生很大的误差。

对于公式（9），v重新定义为：

当wj=1时，式（10）即为式（9）。在噪声环境中，基于欧氏距离的目标函数产生的结果极易受到噪声的干扰。如果对于噪声点和非噪声点赋予不同的比重，那么对于中心计算的误差会大大减小[8]。因此，定义一个新的距离度量：

β是一个正数，想要式（10）成为一个新的距离度量，需要满足距离度量的以下三个条件：

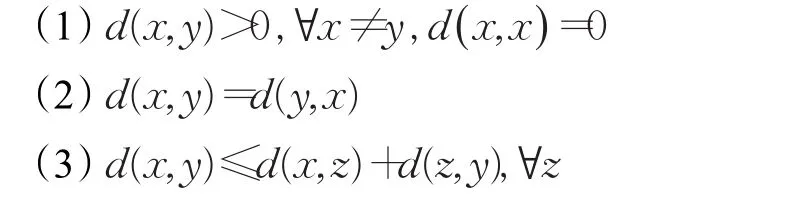
条件（1）、（2）显然成立，条件（3）的证明如下：

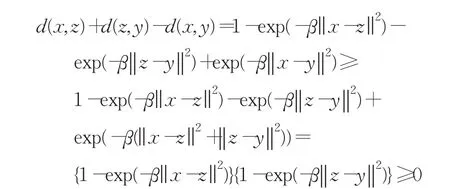
对于数据集X={x1,x2,…,xn}，每个样本点到中心的距离度量定义为：

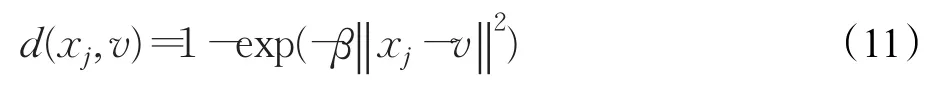
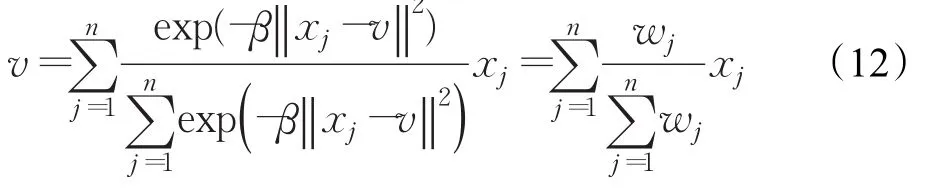
β是一个常数，定义为：

其中：

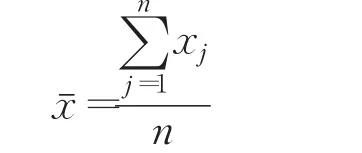
得到新的距离度量计算方法后，本文中样本点到距离中心度量变为：，将其带入改进的目标函数公式（6）中，得：

现在要对目标函数（14）求极值，于是分别对uij和vi分别求导。首先将约束条件（2）拿到目标函数中，那么式（14）变为：

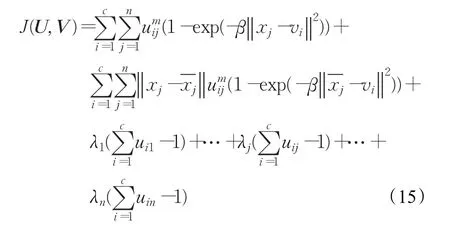
展开式（15）对uij求导使其等于0：

将上式化简，并根据约束条件（2）进一步化简得：

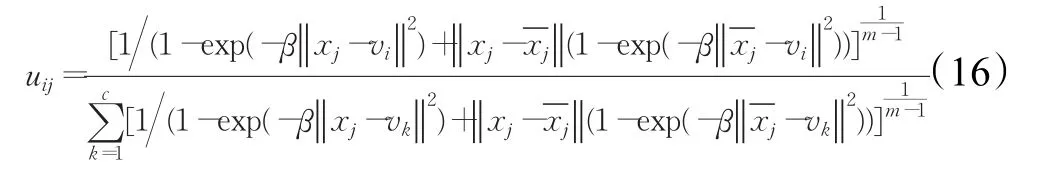
然后对vi求导使其等于0：

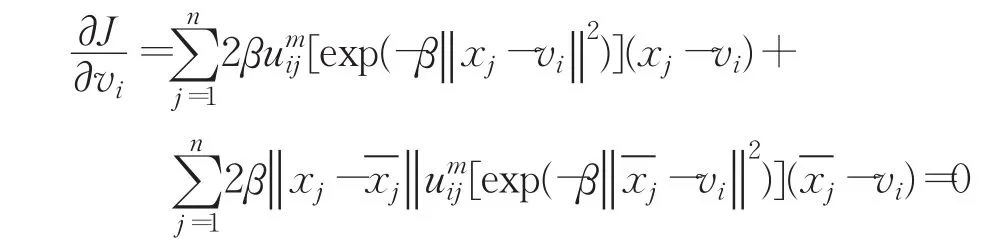
将上式化简得：

通过以上推倒，得出一种新的距离量度公式（11），并基于新的目标函数（14）提出了新的隶属度矩阵（16）和聚类中心（17）。

3.2.3 与Mahalanobis距离对比

Mahalanobis距离也是对传统欧式距离的改进，考虑到各种特性之间的联系，引入了协方差矩阵[9]。由于Mahalanobis距离计算仅涉及协方差矩阵的求逆，不再和特征矢量的维度有关，而是和样本数目有关，因此在高维特征空间计算中带来了优势。

设X为一个l×n的矩阵，l为样本个数，xi∈Rn，i=1,2…,l，样本xi到总体X的马氏距离可以表示为：

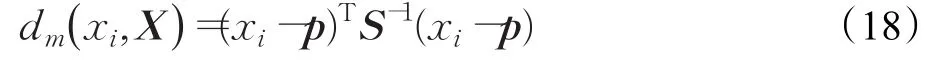
其中，p为所有样本的均值向量，S为协方差矩阵，表示为：

两个样本的马氏距离可以表示为：

于是，基于马氏距离的FCM算法的目标函数可表示为：

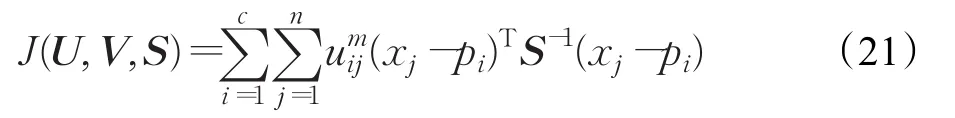
马氏距离与本文距离量度相比，通过协方差矩阵建立样本之间的联系，使样本与聚类中心之间的关系紧密的联系在了一起，虽然它克服了欧式距离不考虑维度之间差异造成一致性聚类的缺点，但是马氏距离依赖协方差矩阵，夸大了变化微小的变量的作用，在抗噪性方面不如本文提出的距离量度。本文距离量度具有很好的鲁棒性，但当样本维度较高且维度之间量纲不同时，计算复杂，此时马氏距离则可以较好的解决高维度的计算问题。本文针对光缆图像的R、G、B三个维度讨论，结合图像采集时易受噪声干扰的特点，本文提出的距离量度是合理适用的。

3.3 算法流程

通过增加邻域信息和改进欧氏距离，得到新的隶属矩阵和聚类中心的计算方法，改进的算法具体步骤如下：

（1）初始化聚类数C=2，模糊加权m=2，根据直方初始化聚类中心V并标准化，设定收敛精度ξ=10-6，初始化迭代次数t。

（2）根据公式（16）更新U 。

（4）计算每个像素和邻域平均值的差异值。

（5）根据公式（17）更新聚类中心V 。

（6）根据公式（16），利用V 更新隶属矩阵U(K+1)。

4 实验与结果分析

4.1 实验步骤

maxl、minl分别表示第l维的最大值、最小值，x(l)是第l维的数据，g(l)是第l维缩放后的数据。

步骤3给图像上添加噪声。

步骤4执行改进的FCM算法步骤。

步骤5根据最终的隶属矩阵U，进行图像分割。

步骤1使用CCD相机获取图片，读取图像数据。

步骤2图像数据预处理：

对图像数据进行标准化，即对每个样本点的RGB三个维度上进行缩放，使其值位于[0，1]区间内，缩放公式如下：

4.2 光缆表面瑕疵图像分割效果

为了验证算法对光缆表面瑕疵检测的效果和算法的性能，本文进行了相关的实验。实验编程环境为Microsoft Visual Studio2010，编程语言为C++；相关实验参数：聚类数为2，模糊加权指数为2，收敛精度为0.000 001。

首先对图像添加椒盐白噪声和高斯噪声，并用FCM算法、基于马氏距离的FCM（FCMM）算法本文的算法进行分割实验。

从图4可以看出，在对叠加了椒盐噪声的光缆图像分割中，FCM算法分割效果并不理想[11]，存在较多的噪声点且目标边缘没有很好的分割，FCMM算法有较好的分割效果但是并没有很好地抗噪性。本文算法以上两种算法相比，受噪声影响极小，对椒盐噪声具有很好的抗干扰能力；从图5可以看出，在对叠加了高斯噪声的光缆图像分割中，FCM和FCCM算法分割结果中存在噪声较多，本文算法噪声影响程度很小，在分割质量上有很大改善。除了人为添加噪声，在光缆检测过程中，CCD相机获取的图片由于光线的原因，会在图像上呈现不同亮斑或暗斑，影响分割效果，如图6所示，由于光照强度的不同，FCM算法将图（a）右边部分识别成了瑕疵，FCMM算法和本文算法则很好的将瑕疵完整分割出来。

图4 图像添加椒盐噪声分割结果

为量化评定算法的分割精度，定义分割正确率SA，通过对SA的计算来说明本文算法的优势。SA表示正确划分的像素数目占聚类图像总像素数的比例[12]，定义为：

式中，c是聚类数目，Ai表示根据算法归类到第i类的像素集合，Ci表示原分割图像中隶属第i类的像素集合。

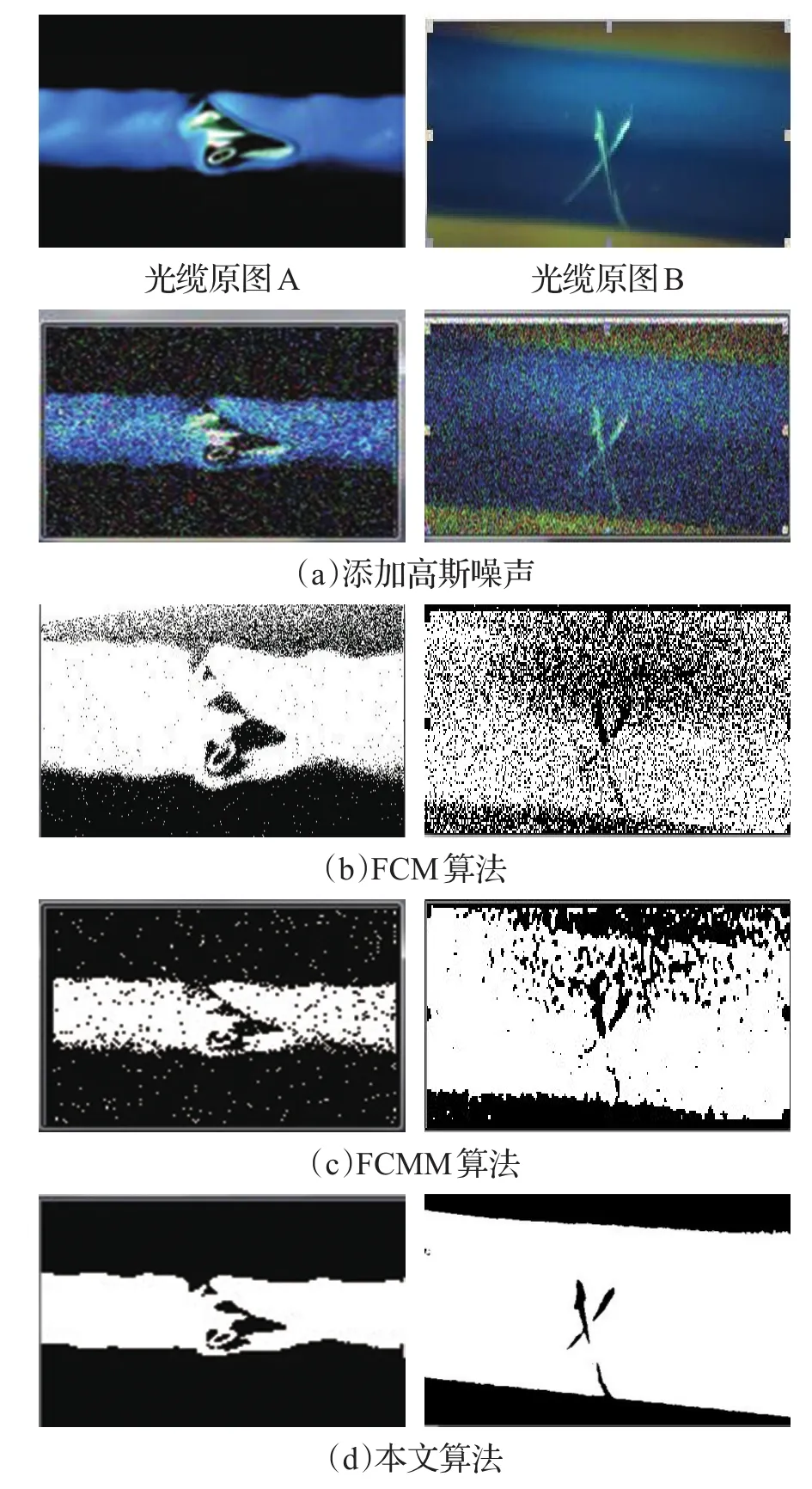
图5 图像添加高斯噪声分割结果

图6 图像分割结果

从表2量化后的精度对比，本文算法的分割率最高，较FCM和FCMM算法有较大改进，从表3可以看出，虽然直方图的初始化方式可以减少迭代次数，但由于本文算法考虑了像素的邻域信息，增加了聚类的复杂度，使得聚类效率不够高。

表2 不同算法对光缆图像的分割正确率%

表3 不同算法对光缆图像的聚类时间 ms

综上，使用本文改进的FCM算法分割光缆瑕疵图像，抗噪和分割效果明显。通过直方图初始化聚类中心，克服了随机性，提高了图像分割的效率。通过增加样本邻域像素信息和改进欧氏距离[13]，有效地提高了图像分割的精度，但还存在效率不够高的问题。

5 结束语

在图像分割中，FCM算法具有描述简单，容易实现，分割效果好的特点，因此广受欢迎[14]。但在实际生产环境中进行光缆检测时，由于周围环境的影响，很容易将噪声引入图像。通过引入新的距离量度和像素邻域信息，对目标函数进行了修正，得到了新的隶属度和聚类中心函数[15]。通过实验验证，与传统FCM算法、FCMM算法相比，改进的算法具有更高的分割效率和精度，克服了FCM算法鲁棒性差的不足。但如何提高效率，平衡分割精度和效率使其达到最优化，还值得进一步深入研究。