结合NSST与GA参数优化PCNN图像融合

刘 栋，聂仁灿，周冬明，侯瑞超，熊 磊

云南大学 信息学院，昆明 650500

1 引言

图像融合（Image Fusion，IF）是指将多源信道所采集到的关于同一目标的图像数据经过图像处理和计算机技术等，最大限度地提取各自信道中的有用信息，最后综合成高质量的图像，以提高图像信息的利用率，改善计算机解译精度和可靠性，提升原始图像的空间分辨率和光谱分辨率。纵观图像融合技术的发展历史，脉冲耦合神经网络（Pulse Coupled Neural Network，PCNN）在图像融合领域已成为研究热点[1-2]，图像融合效果得到进一步改善。PCNN作为第三代的人工神经网络，它与传统人工神经网络的不同之处在于PCNN是一个单一的二维连接网络，并且不需要对PCNN进行训练便可以直接应用。近年来，越来越多的基于PCNN的图像融合算法相继被提出，例如：基于非下采样剪切波变换（Non-Subsampled Shearlets Transform，NSST）的PCNN图像融合（NSST-PCNN）[3-4]；利用空间频率（Space Frequency，SF）驱动PCNN的改进型NSST变换等。

在本文中，提出了一种基于非下采样剪切波变换（NSST）结合遗传算法（GA）来优化PCNN参数的图像融合算法。NSST将非下采样拉普拉斯金字塔变换（Non-Subsampled Laplacian Pyramid transformation，NSP）与多个剪切滤波器及方向滤波器组（Directional Filter Bank，DFB）结合在一起，NSST具有更好的稀疏表示能力和更小的计算代价，同时，PCNN在图像处理领域也展现出一种无与伦比的优势[5]。因此，本文运用遗传算法对PCNN进行了参数的优化，利用其在空间频域（Spatial Frequency）内的作用效果，并与NSST相结合，提出了一种经过参数优化后的NSST-SF-PCNN图像融合方法，该方法吸收了NSST和PCNN在图像处理领域的共同优势。在图像融合过程中，首先，利用NSST对两幅源图像进行分解，分别得到两幅图像的高频和低频系数（AHigh、BHigh），利用经GA参数优化的SFPCNN和SML分别对高频、低频系数进行融合，然后通过逆NSST变换得到融合图像。为了验证所提方法的有效性，与NSST-SF-PCNN方法[5]、PCNN方法[6]、NSST-PCNN方法[7]做了对比实验，其主观及客观结果均显示本文方法在多聚焦图像及医学图像的融合方面有着一定优越性。

2 PCNN模型及其参数优化

2.1 PCNN模型

PCNN是一种基于猫的视觉原理所构建的简化神经网络模型，它是根据猫、猴等动物的大脑皮层上的同步脉冲发放现象而提出的一种具有生物学的背景的人工神经网络。与BP神经网络和Kohonen神经网络相比，PCNN省去了数据学习训练的麻烦，便能从复杂背景下提取出有效的图像信息，同时PCNN还具备同步脉冲发放和全局耦合等优势，因而它能保留图像更多的细节信息，PCNN模型中的神经元唯一对应着图像中的一个像素点，这些优势使得PCNN在图像融合、分割、边缘检测、目标识别等方面均有着广泛的应用。PCNN是由若干个PCNN神经元互连所构成的反馈型人工神经网络，其每一神经元由三部分组成：接受域、调制域和脉冲产生器[8]，其结构如图1所示，在PCNN模型中，脉冲发生器由对网络输出进行漏电容积分的变阈值特性和硬限幅函数组成，其中变阈值特性用来对神经元进行激活，而硬限幅函数则起到抑制该神经元的作用，由此，便可以实现对神经元的“点火”。PCNN的数学模型可由以下几个数学表达式构成[9]：

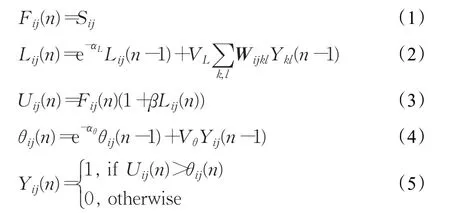
式中，下标ij表示单个神经元所在位置，n表示当前迭代次数，β为链接强度，αL、αθ表示相应的时间衰减常数，其中神经元内部状态Uij由链接器以乘积耦合形式构成，它表示该神经元在其邻域内与其他神经元的信息传递；馈送输入Fij和链接输入Lij由接受域的两个分支形成，并且Fij、Lij是分别以相对较小或较大的时间常数对神经元某邻域内的其他神经元输出进行漏电容积分的加权和的结果；Sij为神经元的外部刺激，即当前系数的拉普拉斯能量和（SML），它将作用于馈送输入Fij；Wijkl为链接权矩阵；VL、Vθ为幅度常数；θij为动态阈值；Yij为神经元的二值输出结果。

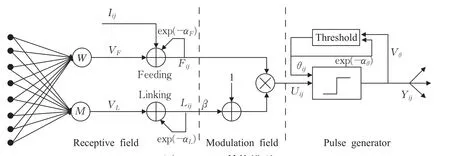
图1 PCNN结构模型

在图像融合中，PCNN模型中的参数设置对于融合效果有着很大的影响，因此为了得到相对较好的效果，摒弃了传统的PCNN参数设置，利用遗传算法（GA）对其参数进行了优化处理，得到了一组优化后的数据作为PCNN图像融合参数。

2.2 遗传算法

遗传算法[10]（GA）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。遗传算法是从代表问题可能潜在的解集的一个种群（Population）开始的，而一个种群则由经过基因（Gene）编码的一定数目的个体（Individual）组成。每个个体实际上是染色体（Chromosome）带有特征的实体。染色体作为遗传物质的主要载体，即多个基因的集合，其内部表现（即基因型）是某种基因组合，它决定了个体的形状的外部表现，如黑头发的特征是由染色体中控制这一特征的某种基因组合决定的。因此，在一开始需要实现从表现型到基因型的映射即编码工作。由于仿照基因编码的工作很复杂，往往进行简化，如二进制编码，初始种群产生之后，按照适者生存和优胜劣汰的原理，逐代（Generation）演化产生出越来越好的近似解，随着不断的迭代，当满足终止条件时，所求的值逼近最优解，在每一代，根据问题域中个体的适应度（Fitness）大小选择（Selection）个体，并借助于自然遗传学的遗传算子（Genetic Operators）进行组合交叉（Crossover）和变异（Mutation），产生出代表新的解集的种群。这个过程将导致种群像自然进化一样，后代种群比前代更加适应于环境，末代种群中的最优个体经过解码（Decoding），可以作为问题近似最优解。

2.3 GA参数优化过程

在基于PCNN的图像融合过程中，需要研究人员对PCNN的各个参数进行设置，在传统的应用中，其参数往往是凭人工经验来设置的，然而对于不同的图像，往往需要设置不同的参数，以达到一个更好的融合效果，所以引入GA来对PCNN的参数进行优化，可以根据不同的需要自动选择并设置合适的参数，省去了人工试验的麻烦。在此PCNN数学模型中，需要设置的参数有：链接强度β、时间衰减常数αθ、幅度常数Vθ、链接权矩阵Wijkl以及阈值θ。传统PCNN参数设置为：β=0.1，θ=0，αθ=20，Vθ=0.2，VL=1，n=200，Wijkl=[0.5 1 0.5;1 0 1;0.5 1 0.5]。

如图2所示，根据遗传算法流程图，基于GA的PCNN参数优化步骤如下[11]。

步骤1初始化：以图像融合客观评价指标为遗传算法目标函数，首先对参数进行初始化，种群大小为40，最大遗传代数为20，初始交叉及变异概率分别为0.7和0.35；然后进行个体初始化，利用随机函数的循环工作，随机生成0-1之间的8个数值，对这8个数值进行基因判断，若大于0.5，则该位为1，否则为0。

步骤2编码：由于PCNN模型的输出只有0和1，所以采用简单实用的二进制编码的方式对待求解的参数进行编码，以产生初始种群。

步骤3适应度的计算：设高于或低于给定阈值的灰度值和像素数的总和分别为hs、ls和hn、ln，并分别计算其平均灰度值：U1=ls/ln，U2=hs/hn，则单一个体的适应度可由下式计算得出：

步骤4按照从小到大的顺序对适应度进行排序，并统计出最优阈值及最优适应度。

步骤5选择：适应度值越大的个体，被选择的概率越大，选择优胜的父代个体以保留到子带中，以精英选择的方式进行选择操作，将适应度值较大的前5%的优良父本复制到子带中，对剩下的父本个体执行交叉和变异操作。

步骤6交叉：当满足交叉条件时，随机选取偶数对的父本进行两两配对，并随机交换对应位置上的基因。

步骤7变异：执行变异操作以保持种群的多样性，避免某些信息的过早丢失，同时对各代中的基因变异个数进行计算，确定其变异位置及编号，并进行0、1互换的变异操作。

步骤8重复以上步骤，直到满足终止条件或达到最大遗传代数时停止实验，得出最佳阈值，代入程序中进行实验。

经过以上参数优化步骤后，确定PCNN待优化参数β、αθ、Vθ的值并带入程序实验，当取Wijkl=[0.707 1 0.707;1 0 1;0.707 1 0.707]时，图像融合效果更佳，另外取VL=1，n=200与传统设置值一致。

图2 遗传算法流程图

3 NSST变换

轮廓波（Shearlet）变换是由Labate等人在小波变换基础上提出的[12-13]，其仿射变换二维表达式如下：

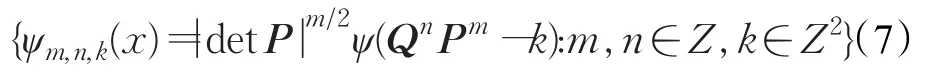
在NSST变换中，NSST包含非下采样金字塔滤波器（NSP）和剪切滤波器（SF）两部分。NSP被用来代替剪切波变换，这种操作避免了上采样和下采样带来的影响，源图像在经过NSP分解后，会产生大小相同的低频子带和高频子带，如图3、图4所示。对产生的低频子带进行k级NSP分解，最终会形成大小相同的1个低频子带和k个高频子带[7]。

图3 剪切波诱发频率结构图

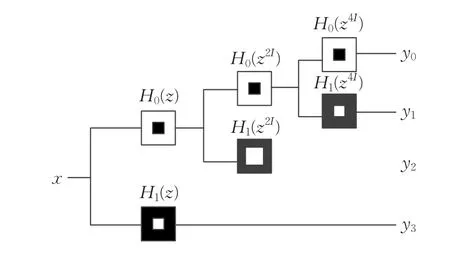
图4 NSP分解过程

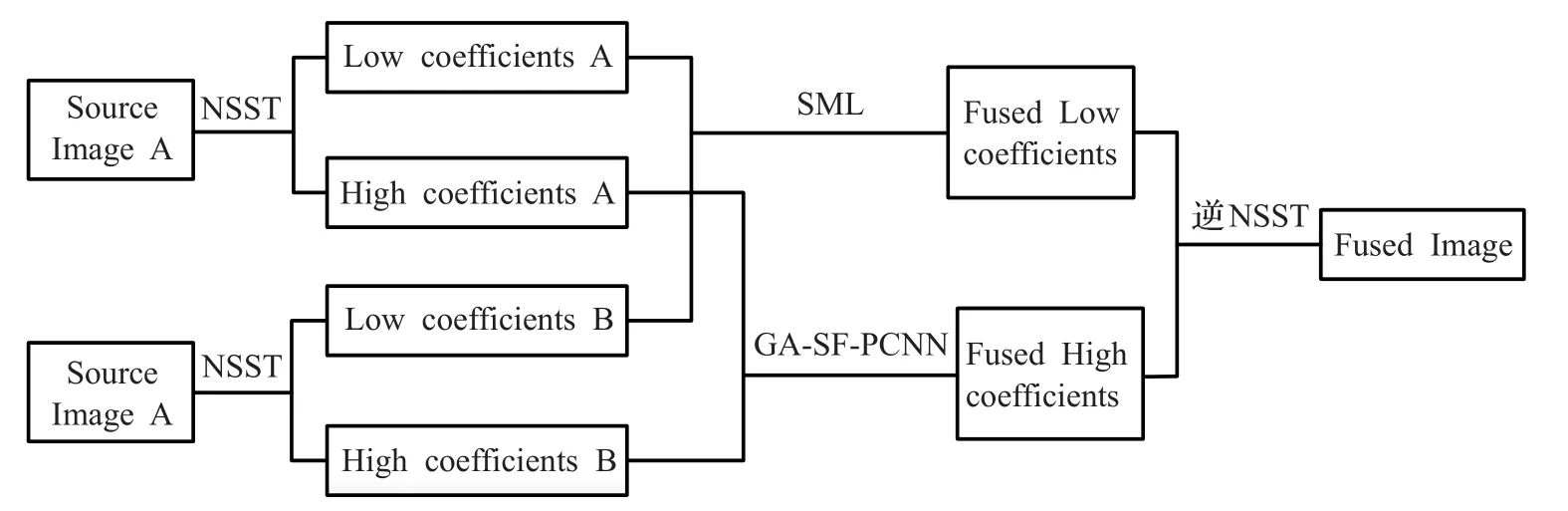
图5 NSST-GA-SF-PCNN图像融合结构图

4 算法实现

4.1 算法流程

传统的PCNN模型一般是由一个单一系数来进行驱动的，然而人类视觉系统通常对图像的特征较为敏感。在基于PCNN的图像处理领域中，图像空间频率（Spatial Frequence，SF）[14]通常被视为图像的梯度特征，因此为了获得更好的融合效果，本文利用SF来驱动PCNN模型。SF通过使用子带中系数的滑动窗口来测量，通过行和列中的梯度能量来衡量基于窗口的系统中的整个活动，每个子带中的SF被输入到PCNN以激励神经元并产生神经元脉冲，SF可由下式定义：

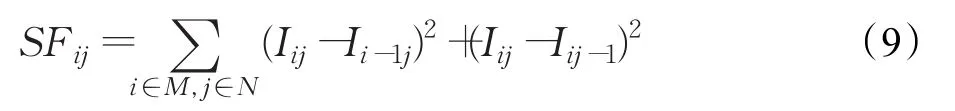
本文提出了一种基于GA参数优化的SF-PCNN模型在NSST域内的图像融合算法，为了验证该算法的优越性，本文将该算法与已有算法（NSST-SF-PCNN[5]、PCNN[6]、NSST-PCNN[7]）的图像融合效果进行比较，并通过计算客观评价指标（互信息MI、图像边缘信息保留量QAB/F、图像信息熵EN、空间频率SF、图像标准差STD和图像平均梯度AG）的数值进行客观比较说明。本文算法结构流程如图5所示，该算法的图像融合步骤如下：

（1）通过NSST变换对两幅实验源图像进行多尺度分解，得到大小相同的高频和低频子带。

（2）运用经过参数优化后的SF-PCNN和SML融合规则分别对高频系数和低频系数进行融合，得到高频融合点火图像和低频融合点火图像。

（3）通过逆变换NSST，对高、低频点火图像进行融合，得到最终融合图像。

（4）计算客观评价指标，通过实验与相关算法比较，得出结论。

4.2 高频子带融合规则

由于人类视觉系统在直观上对图像的边缘等特征更为敏感，所以传统单纯使用单一子带系数作为PCNN输入来驱动PCNN是不够的。因此，在文献[14]中，Qu等人使用空间频率（SF）作为输入来驱动PCNN，图像的SF反映的是一幅图像的总体活跃程度，SF越大，图像活跃度越高，相应图像也就越清晰。根据文献[14]，一种改进的空间频率可由如下公式定义：

式中，SF为图像空间频率，RF、CF、DF1、DF2分别为图像行频率、列频率和两个对角频率。在式（1）中，取Fij(n)=SF作为PCNN的输入刺激。

4.3 低频子带融合规则（SML）

在经过NSST变换分解后的图像所得到的低频子带中，包含了源图像中大量的能量信息[15]。为了更好地展示图像的灰度信息的突变，并在一定程度上更好地反映出图像边缘的变化，文献[16-17]提出了运用拉普拉斯能量和（SML）的低频子带融合规则，实验证明SML在图像低频子带系数的融合中有良好的效果，能更好地辨别图像的清晰度。像素(x,y)的拉普拉斯能量和SML可由以下公式定义：

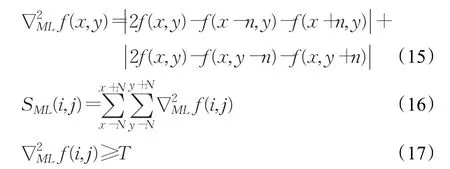
式中，n表示用离散差分求拉普拉斯梯度时采用的空域间隔，通常取n=1，N=4，T=0为门限值[18]。

5 实验结果及分析

本次实验运行环境为Intel Corel 2，CPU 3.00 GHz，内存4 GB，Windows 7操作系统，MATLAB R2014a。为了验证算法的有效性，本文选取多聚焦实验图像Clock、医学图像和红外与可见光图像分别进行实验得出其融合图像，将经过GA优化后得到的PCNN参数代入程序中，运行并分别计算其互信息MI、图像品质因数QAB/F、图像信息熵EN、空间频率SF、标准差STD和平均梯度AG的值与对比实验方法所得出的值进行比较。多聚焦图像、医学图像和红外及可见光图像融合对比结果，如图6、图7和图8所示。客观评价指标如表1、表2和表3所示。

图6 Clock多聚焦图像对比实验结果

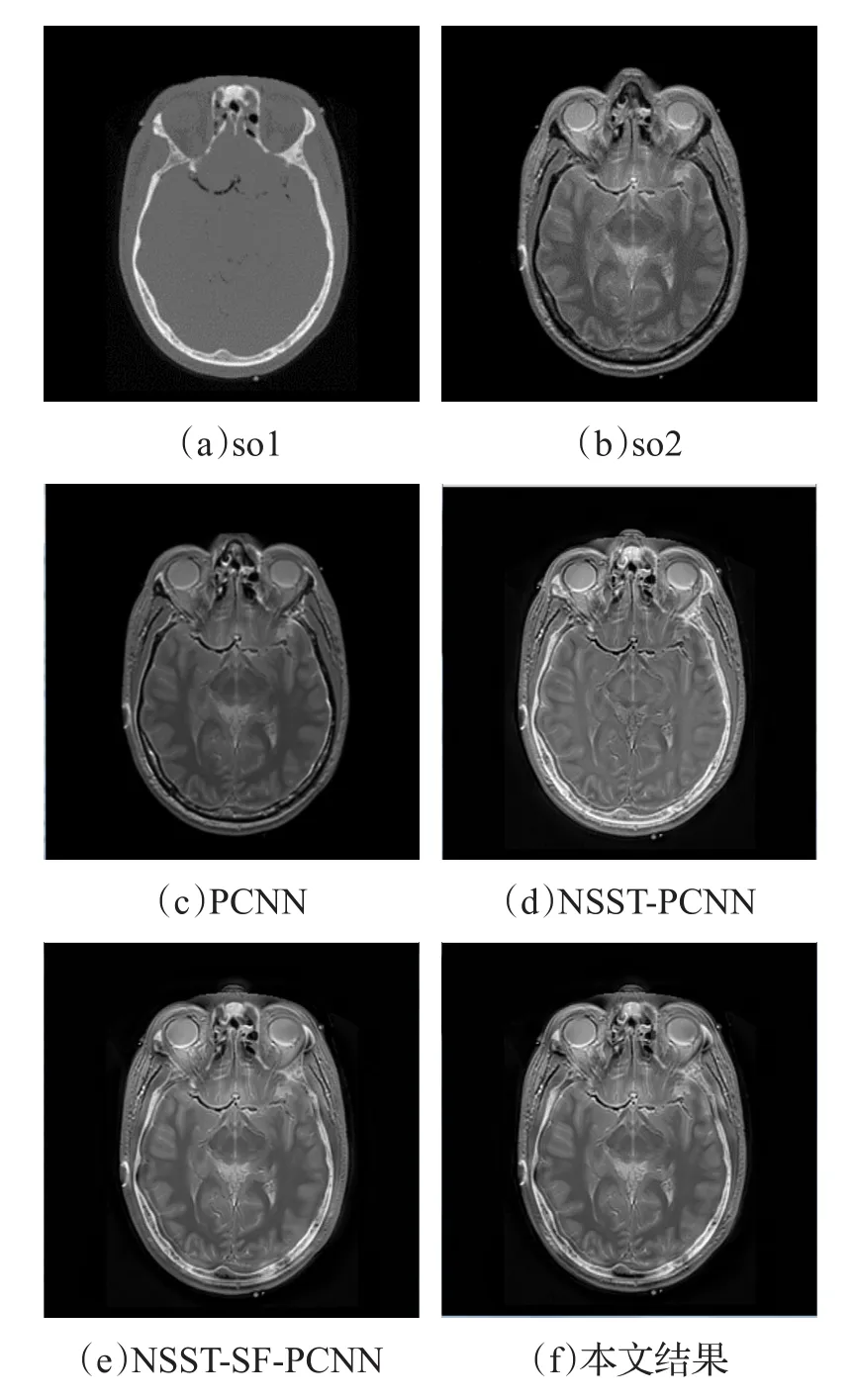
图7 医学图像对比实验结果

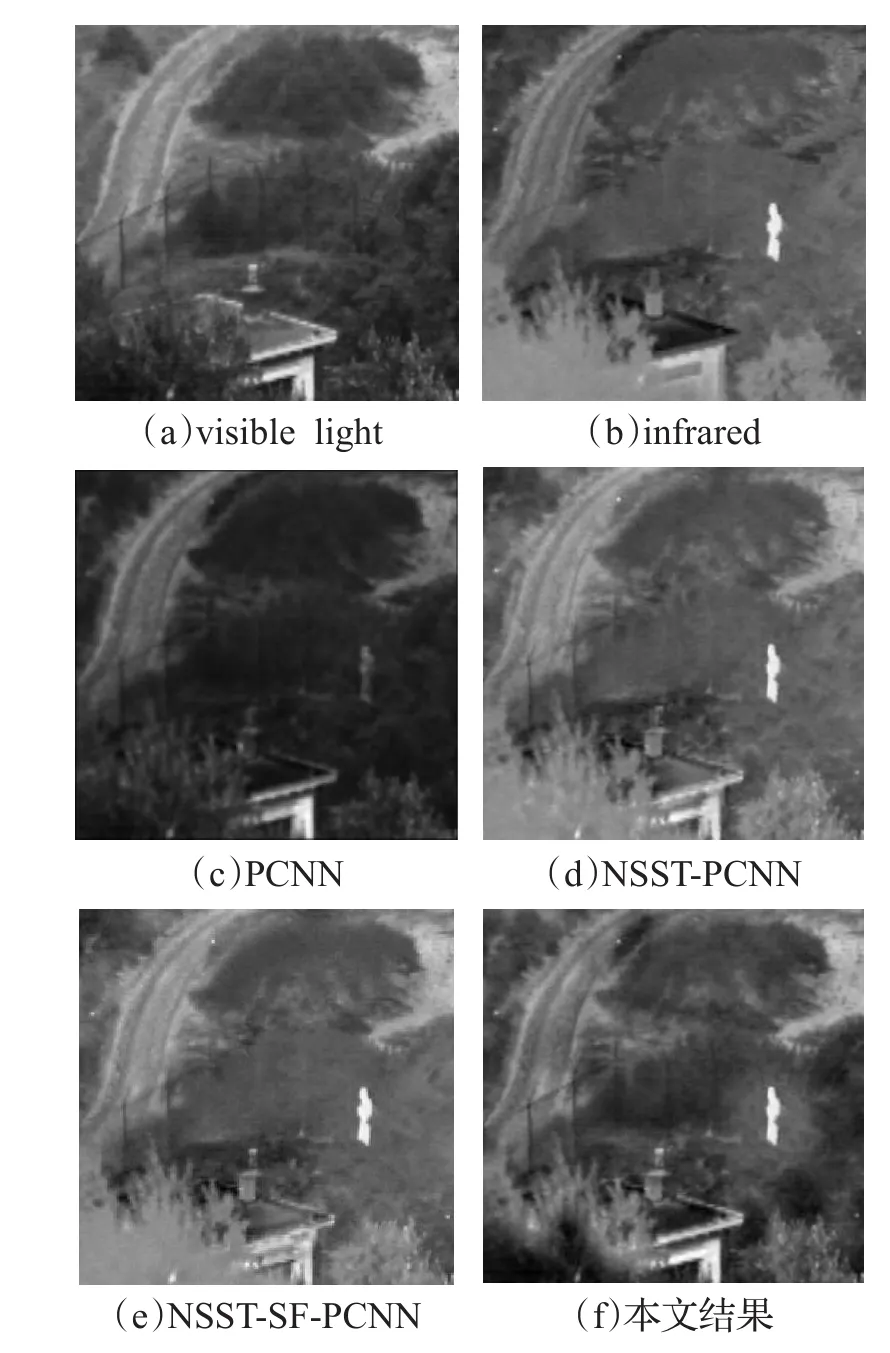
图8 红外及可见光图像融合实验结果

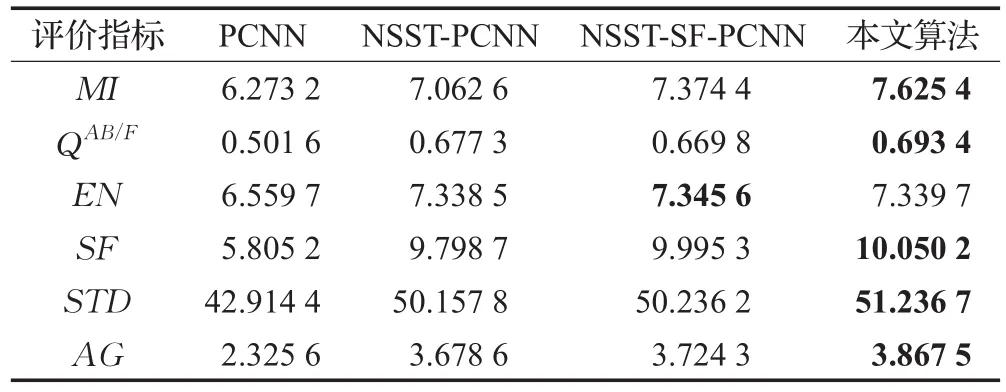
表1 图像Clock融合结果评价指标

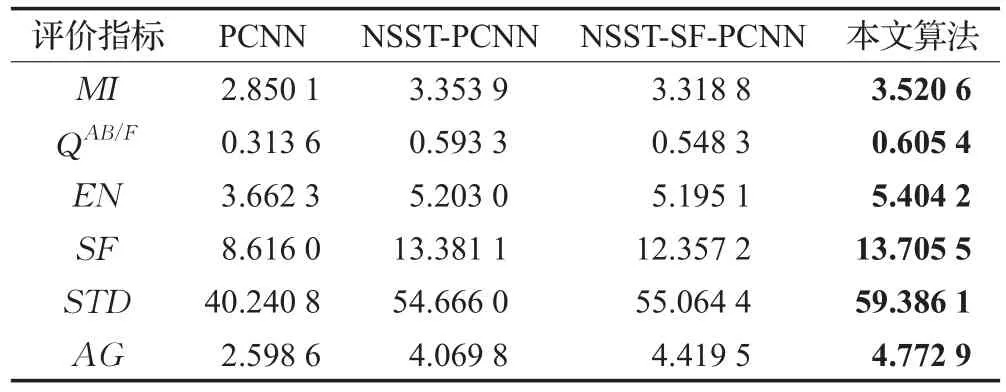
表2 医学图像融合结果评价指标

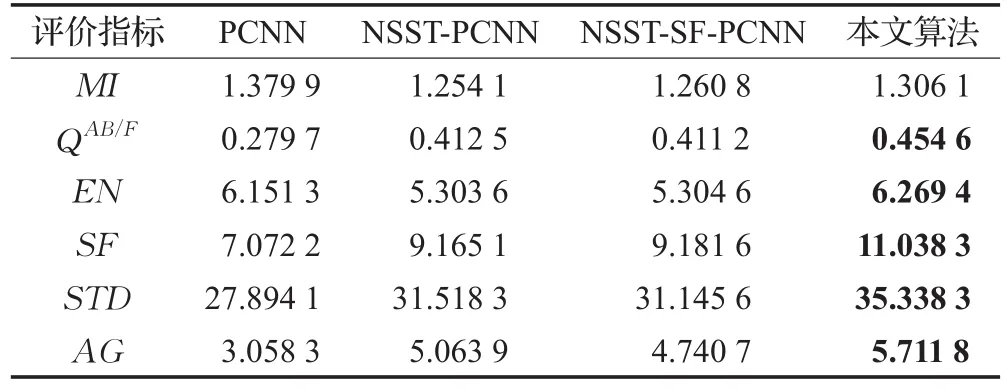
表3 红外及可见光图像融合结果评价指标

6 结论

本文运用遗传算法对PCNN参数进行优化后，利用NSST对源图像进行分解得到高频和低频子带，用SML、GA优化SF-PCNN分别对低频子带、高频子带进行融合，再利用NSST逆变换来获得最终融合图像。从主观视觉来看，本文图像融合结果也要优于对比实验结果，同时通过对表1、表2和表3的图像融合质量客观评价指标的对比，可以看到本文算法在图像互信息MI、图像边缘信息保留量QAB/F、图像信息熵EN、图像空间频率SF、图像标准差STD和图像平均梯度AG等6个指标中，几乎全部的指标值都要优于对比方法的值，这几个指标的值越大，说明图像融合的效果越好，这也恰恰说明使用本文算法对PCNN的重要参数进行GA优化后，使得多聚焦图像、医学图像及红外与可见光融合的效果都得到了一定的改善。