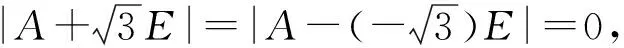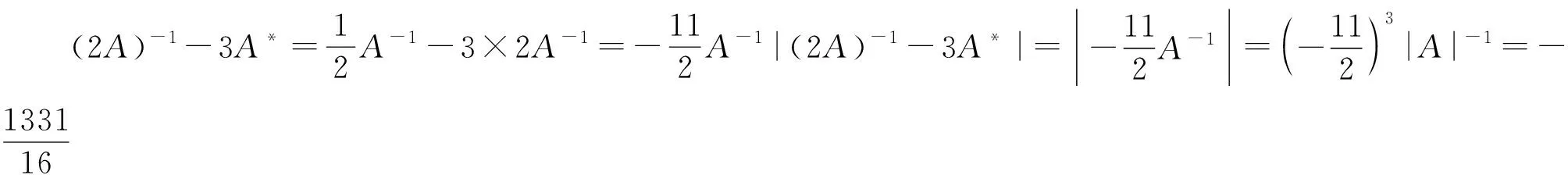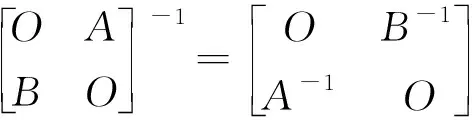关于伴随矩阵的性质及应用的研究
董改芳
(朔州师范高等专科学校,山西 朔州 036000)

1 伴随矩阵的常用性质
性质1AA*=A*A=|A|E
证明 令A=(aij)n×n,根据伴随矩阵定义,有
由行列式按一列展开公式可以得

E为n级单位矩阵,同样由行列式按行展开公式可以得AA*=|A|E得证。
性质2 若|A|≠0则A*=|A|A-1
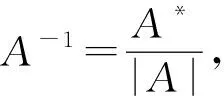
性质3 |A*|=|A|n-1
证明 (1)若|A|≠0,由性质2有A*=|A|A-1,两边取行列式得|A*|=||A|A-1|=|A|n|A|-1=|A|n-1
(2)若|A|=0,由性质1可知,AA*=O,从而有r(A)+r(A*)≤n,
当r(A)=0,即A=O时,A*=O,|A*|=|A|n-1,结论成立,
当r(A)≥1时,r(A)+r(A*)≤n,所以r(A*)≤n-1,即A*不是满秩的,|A*|=0,
因而|A*|=|A|n-1, 得证。
性质3给出了伴随矩阵的行列式的性质。
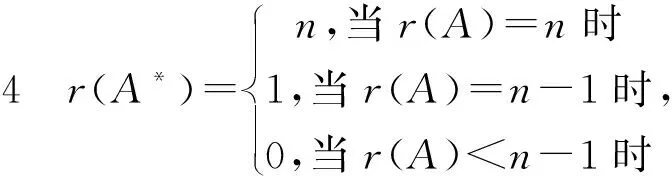
证明 (1)当r(A)=n时,由A*=|A|A-1可知,A*可逆,r(A*)=n。
(2)当r(A)=n-1时,AA*=|A|E=O,有r(A)+r(A*)≤n,r(A*)≤n-r(A)=1
若r(A*)=0,则

(3)若r(A) 性质4给出了矩阵的秩r(A)和它的伴随矩阵的秩r(A*)的关系。 性质5 (A*)*=|A|n-2A,这里A为n(n>2)级方阵。 证明 由性质1AA*=A*A=|A|E可知 (1)当|A|≠0时,A*=|A|A-1,于是 (2)当|A|=0时,由性质4: 可知,r(A*)≤1,当n>2时,r((A*)*)=0,从而有 (A*)*=O,因此(A*)*=|A|n-2A,得证。 性质7A是正交矩阵,则A*也是正交矩阵。 证明 由A是正交矩阵可得 AA′=E,且|A|2=1。 (A*)′A*=(|A|A-1)′(|A|A-1)=|A|2(A-1)′(A-1)=(A′)-1A-1=(AA′)-1=E 所以A*也是正交矩阵 性质8A是正定矩阵,则A*也是正定矩阵。 证明 由A是正定矩阵可知:A与单位矩阵合同,即存在可逆矩阵C 使得C′AC=E从而有 (C′AC)*=C*A*(C′)*=C*A*C(C*)′=E 所以A*也是正定矩阵。 性质9 若λ是可逆方阵A的特征值,α是A的属于λ的特征向量,则λ-1|A|是A*的特征值,α是A*的属于λ-1|A|的特征向量。 例1 设 求(A*)-1 方法技巧:利用性质9,已知λ是可逆阵A的特征值,α是属于λ的特征向量,只需求|A|,则λ-1|A|是A*的特征值,α是A*的属于λ-1|A|的特征向量。 例3 设A是三级矩阵,|A|=2,求|(2A)-1-3A*|的值。 方法技巧:利用了性质2,A*=|A|A-1和对于n级矩阵有|λA|=λn|A|。 例4 设A是n级方阵,且|A|=a≠0,求|A*|。 解 由性质3可知,|A*|=|A|n-1=an-1。 方法技巧:利用了性质3,|A*|=|A|n-1。 伴随矩阵连接了可逆矩阵和其逆矩阵,是它们之间的桥梁。在矩阵理论中也有非常重要的作用,所以讨论伴随矩阵的常用性质和其应用是非常必要的。希望本文能使大家对伴随矩阵的定义有更深入的理解。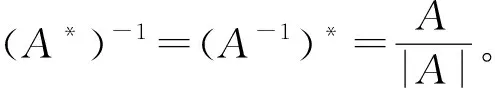

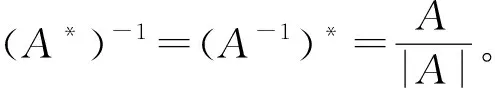
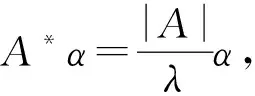
2 伴随矩阵的性质的应用