含不确定性的连续时间脉冲奇异系统的有限时间滤波

李文姿

(山西大学商务学院,山西 太原 030031)

引言

滤波是控制理论界的研究热点之一。在系统噪声统计特性无法获知时,将噪声当作能量有限的随机信号,使系统从扰动到估计误差的闭环传递函数的H∞范数小于某个给定的值,从而设计所需的H∞滤波器。H∞滤波有效克服了维纳滤波的缺点,受到了诸多学者的关注[1-3]。另外,在实际应用中,有时仅需关注系统状态在一个有限时间段内的行为,因此有限时间滤波问题的研究成为了控制理论研究的一个重要组成部分,也取得了很多成果[4-7]。

另一方面,不确定性是影响系统性能的一个关键因素。实际应用中,难以避免的不确定因素常与指定的性能指标是矛盾的,也会引起系统的不稳定性。因此,许多学者在研究中,将系统的不确定性考虑进去,使其在一定变化范围内能满足系统所需要的各项指标。目前,虽然该理论的发展已有丰硕的成果[8-9],但并不是所有的问题都已解决,随着社会的发展,各类新系统的出现,这些系统中含不确定性的控制理论研究给许多学者提出了新的挑战。据此,本文研究了在有限的连续时间段内脉冲奇异系统含不确定性时的滤波问题。

1 预备知识

研究如下的连续时间脉冲奇异系统:

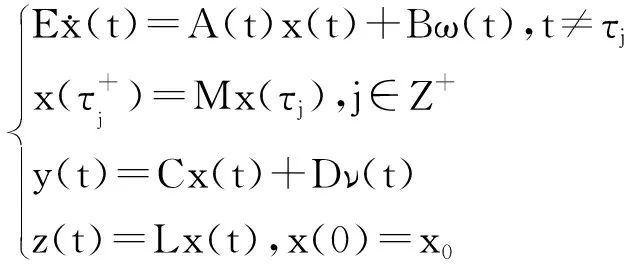
(1)

其中x(t)∈Rn为系统状态,y(t)∈Rl为可控输出,z(t)∈Rp是待测信号,ν(t)∈L2([0,∞),Rr)与ω(t)∈L2([0,∞),Rq)分别为测量噪音和过程噪音,时间列τj为脉冲点，A(t)=A+ΔA(t),ΔA(t)是不确定性时变矩阵,满足

ΔA(t)=GF(t)H

(2)

A,B,M,C,D,G,H是有恰当维数的实常数已知矩阵,F(t)是时变不确定性矩阵,满足FT(t)F(t)≤I,I为恰当维数的单位阵。

为方便研究系统(1),假设满足下列条件:

1)(E,A(t))正则且系统(1)脉冲自由。

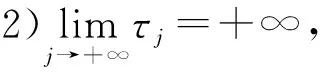
3)对任意给定的d∈R+,ω(t)和ν(t)满足

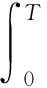
(3)

4)系统的状态在脉冲点τj都左连续。

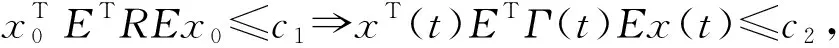
设计一个如下形式的n维线性滤波器:

(4)

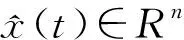
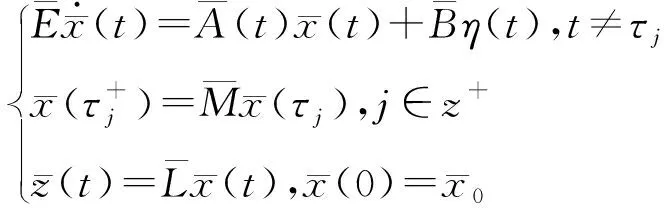
(5)

其中

(6)

研究问题描述如下:

对系统(1) 和给定的噪音抑制水平γ>0,在有限的时间段内考虑设计滤波器(4),使得滤波误差动态系统(5) 是稳定的,且在零初始条件下,对任意非零的η(t)∈L2([0,T],Rq+r),滤波误差满足

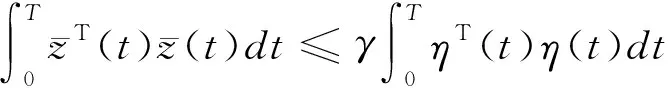
(7)

引理1[10]给定合适阶数的矩阵Y,D和E,其中YT=Y,则Y+DFE+ETFTDT<0对所有满足FTF≤I的F成立,当且仅当∃ε∈R+使得Y+εDDT+ε-1ETE<0。

2 主要结论

定理1 假定(a1)-(a4)成立,如果能找到对称阵P和正常数h满足

(8b)

(8c)

h(λc1+γd)≤c2,

(8d)

其中λ=λmax(R-1P),那么在有限时间段内滤波误差动态系统(5)是稳定的且满足式(7)。

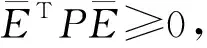
∀t∈(τj,τj+1),j∈Z+,由(8a)可得

≤γηT(t)η(t),

再由(8b)知,

所以∀t∈(τj,τj+1,j∈Z+有

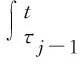
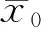
≤h(λc1+γd)≤c2。

由定义1知在有限时间段内滤波误差系统(5)是稳定的。

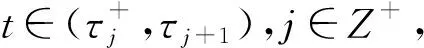
结合条件(8b),则

因此

≤V(0)-V(T),

下面研究滤波器的可解问题。

定理2 假设(a1)-(a4)成立,考虑系统(1)和滤波器(4), 给定正常数γ,若存在对称阵P=diag{P11,P22},矩阵N1,N2,N3和正常数λ,ε,h,满足(8c)和下列条件

(9a)

(9b)

P<λR,

(9c)

(9d)

则滤波问题可解。进一步得到所求滤波器的未

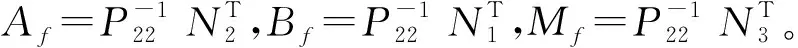
证明 应用Schur补,(8a)等价于

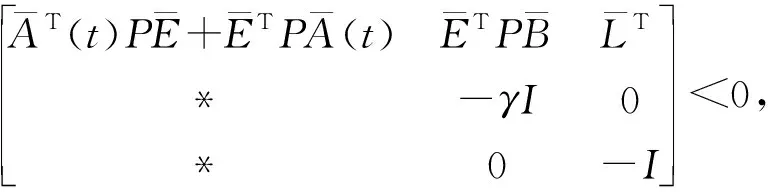
(10)

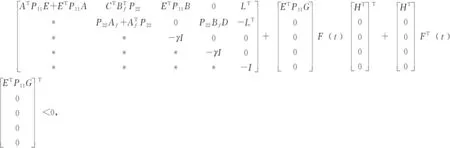
(11)

根据引理1(11)式可等价于∃ε∈R+使得

再应用Schur补该不等式等价于

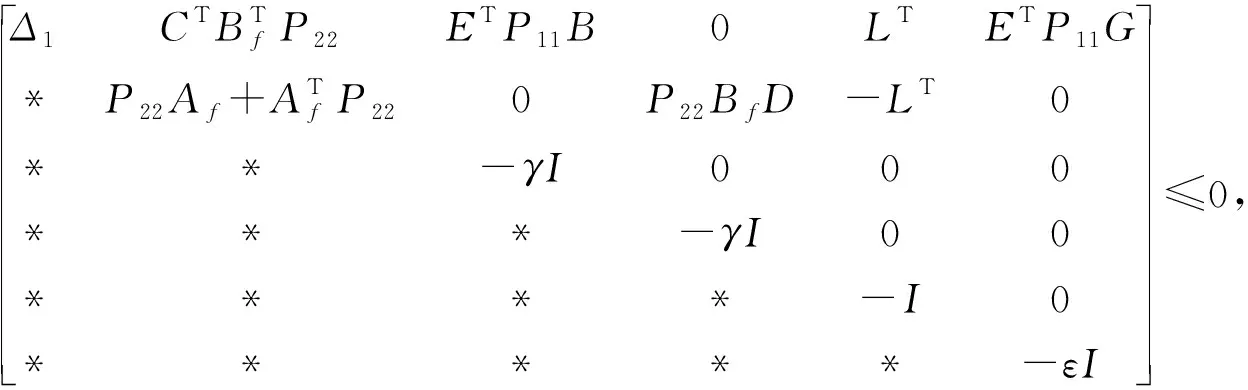
(12)

其中Δ1=ATP11E+ETP11A+εHTH。

同理,把(6)代入(8b),并对其应用Schur补,则(8b)等价于

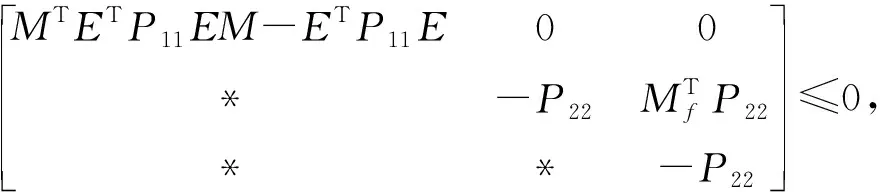
(13)

3 结束语

文章讨论了含不确定性的一类连续脉冲奇异系统的有限时间滤波问题。先给出了该滤波器存在所应满足的充分条件,再将该条件转化成线性矩阵不等式的形式,从而解决了该滤波器的求解问题, 推广了有限时间滤波理论。