改进头脑风暴优化算法与Powell算法结合的医学图像配准
梁志刚,顾军华,2
(1.河北工业大学 电气工程学院,天津300401; 2.河北工业大学 计算机科学与软件学院,天津 300401)
0 引言
图像配准是医学图像分析领域的一个基本问题。临床上医学图像辅助疾病诊断、确定治疗方案、手术模拟和术中导航等[1-2]很多应用,都需要图像的精确配准作为先决条件。医学图像配准是指通过求解两幅或多幅图像间的变换关系,使得同一患者不同时间、不同成像方式得到的图像或者图像中具有诊断意义的特征点在空间上对应起来[3]。图像配准的目的是综合利用多幅图像对同一器官的表达,在一幅图像中同时反映人体器官解剖结构、代谢功能、病理发展等多方面的信息。随着医学影像技术的广泛应用,图像配准在现代医学中发挥着越来越重要的作用,已经成为当前医学图像分析领域的一个热点问题。
医学图像配准就是通过优化算法搜索两幅或多幅图像之间变换参数的过程,本质上是一个参数寻优问题。图像的互信息(Mutual Information, MI)值通常作为优化问题的目标函数,常用的优化算法包括Powell算法[4]、单纯形法[5]、遗传算法(Genetic Algorithm, GA)[6]、蚁群优化(Ant Colony Optimization, ACO)算法[7]、粒子群优化(Particle Swarm Optimization, PSO)算法[8-9]等。由于互信息存在多个局部极值和计算负荷大的问题,因此近年来多选择基于多分辨率分析的优化策略,并采用全局和局部优化算法结合的混合算法以提高速度和精度。杨帆等[10]运用蚁群算法和Powell 算法相结合的多分辨率搜索算法,对三维计算机断层扫描成像(Computed Tomography, CT)和磁共振成像(Magnetic Resonance Imaging, MRI)图像进行配准,得到了亚像素级的配准精度。李超等[11]应用Logistic混沌映射生成可控且可再现遗传算法初始粒子,基于Powell算法与遗传算法结合的混合算法在多分辨率策略下实现了配准,优化了配准精度和性能。赵海峰等[12]提出了一种改进的人工鱼群算法和Powell算法结合的多分辨率医学图像配准算法,提高了配准的精确度和性能。吕晓琪等[13]利用PSO 算法在小波分解低分辨率层粗配准后,将配准参数作为Powell 算法在高分辨率层的配准起始点,实现了快速精确配准。由于蚁群算法和粒子群算法存在群聚效应,容易出现早熟现象,遗传算法和人工鱼群算法计算复杂且精度较差,无法为局部搜索提供可靠的初始解,并且四种算法在极值点附近搜索易出现震荡现象,存在收敛速度慢的问题。
为了解决以上算法精度较差、易陷入局部极值和收敛速度慢的问题,本文结合多分辨率分析,提出改进头脑风暴优化(Modified Brain Storm Optimization, MBSO)算法和Powell算法结合的图像配准算法。头脑风暴优化(Brain Storm Optimization, BSO)算法是Shi[14]于2011年提出的群体智能优化算法,本文提出的MBSO算法对BSO算法全局和局部搜索的调节机制进行了改进,并采用可变步长,能够以较好的精度快速定位问题全局最优解。本文算法在图像小波分解的低分辨率层采用MBSO算法进行全局搜索,快速确定全局配准参数,然后将此参数作为Powell算法初始参数,在高分辨率层进行搜索确定图像最优配准参数。单模和多模图像配准实验表明,本文算法能够快速、准确确定图像配准参数。
1 互信息和多分辨率图像配准
图像配准过程中坐标和角度保持不变的图像称为参考图像,记为R,待配准图像称为浮动图像,记为F。令IR(x,y)和IF(x,y),(x,y)∈Ω⊂R2,分别表示参考图像和浮动图像在(x,y)处的灰度值,Ω表示图像空间。令Tp(x,y)表示作用在浮动图像F坐标(x,y)处像素的刚体变换,p=(tx,ty,θ)表示此变换参数的向量形式,其中(tx,ty)表示x和y方向的平移,θ为旋转角度,变换如式(1)所示:
(1)
对R和F进行配准,实质上寻找最优几何变换T,使得图像间相似性测度函数取得极值:

(2)
其中MI()表示相似性测度。
1.1 互信息原理
基于最大互信息的图像配准方法无需对图像进行预处理和特征点提取,具有鲁棒性强、精度高的优点,已经被广泛应用于医学图像配准研究中。互信息(MI)是信息论中基于熵的测度,描述两个随机变量相关性的度量函数。医学图像的互信息定义为两幅间相似程度,即一幅图像中包含另一幅图像信息量的多少,互信息值越大,则两幅图像相关性越高。一幅图像R的熵表示为:
(3)
其中:N表示图像的最大灰度级别,每个灰度级别i=1,2,…,N出现的概率pi=hi/N,hi为灰度级别i的个数。图像R和F的联合熵由式(4)给出:
(4)
其中:pR,F(r,f)是将R和F两幅图像的灰度值作为随机变量联合概率分布。图像R和F的互信息由式(5)表示:
MI(R,F)=H(R)+H(F)-H(R,F)
(5)
当两幅图像达到最佳配准位置时,联合熵达到最小值,互信息取得最大值。MI并没有解决重叠区域的问题,尤其是当重叠区域灰度值较小时会影响MI的均衡性能,错误的配准同样会使互信息值增大。为了抵消重叠区域的影响,Studholme引入归一化互信息,如式(6)所示:
(6)
归一化互信息抵消了重叠区域的影响,对于配准结果的量化表示更加鲁棒和精确,本文采用归一化互信息作为图像配准的测度。
1.2 多分辨率分析
小波变换是一种时域和频域综合图像分析方法,应用多分辨率将图像分解为不同尺寸、不同分辨率的图像,在较低分辨率图像上进行配准,可以大大降低配准过程中计算联合直方图和插值的时间、空间等计算资源的消耗。对于分辨率为m×n二维图像IR(x,y),通过式(7)可以得到图像的低频部分:
Ik(x,y)=∑∑Ik-1(m,n)h(2m-x)l(2n-y)
(7)
其中:k表示分解层数,h和l分别表示小波分解高通滤波和低通滤波尺度方程系数。
图像经过小波分解后低频近似分量保存了图像的主要信息,在低分辨率层运用全局搜索算法确定配准参数粗略位置后,上升到高分辨率层运用局部搜索算法进一步细化配准结果。低分辨率层运用全局算法搜索,较少的数据量提高了搜索效率,并且使算法跳出局部极值的干扰,为高分辨率层局部搜索提供准确初始点信息,增强整个搜索算法的鲁棒性、提高精度。图像经过小波分解后,配准参数关系如下:高分辨率层平移参数是下一级低分辨率层变换参数的2倍,缩放和旋转参数在各分辨率层相等。基于互信息的多模图像配准中,对于图像只需分解2~3层即可达到配准精度和时间的要求。
2 优化算法
2.1 Powell算法
Powell算法可用于求解一般无约束优化问题,无约束最小化优化问题可以描述为:
minσ=f(x);x∈Rn
(8)
其中:σ=f(x)是优化问题的目标函数,x是n维优化自变量,Rn是优化问题的可行域空间。
Powell算法是一种十分有效的局部直接搜索算法,算法将多维优化问题转化为一维迭代寻优问题,利用共轭方向可以加快收敛速度的性质,在每一维中使用Brent算法进行循环搜索。在寻优过程中,Powell算法不需要对目标函数进行求导,当目标函数的导数不连续时也能应用。
对于(8)的最小化优化问题,给定的初始解,首先沿给定的n个共轭方向进行搜索,接着沿初始点与搜索终点连线方向进行n+1轮搜索,最后用第n+1次方向替换前n个方向中其中一个,开始新的迭代过程。Powell算法在局部搜索中具有很高的精度,并且搜索速度非常快,但是作为一种能力极强的局部搜索算法,依赖于初始点的选择,当初始点选择在局部最优附近时,算法无法跳出局部最优的干扰,很容易陷入局部最优。为了克服Powell算法的这一缺点,首先运用头脑风暴优化算法进行全局搜索,确定全局极值的粗略位置,作为Powell算法的初始点进行局部细致搜索,两种算法的结合可以实现快速、精确、鲁棒的图像配准。
2.2 头脑风暴优化算法
BSO算法是对人类社会行为进行抽象产生的群体智能算法,算法的灵感来自于人类创造性解决问题的方法——头脑风暴(Brain storming)法。头脑风暴法指具有不同专业背景的人或小组围绕一个特定的兴趣或领域,进行发散思维、思想碰撞、观点融合,以找到问题的最优解决方案,是一种激发集体智慧产生和提出创新设想的思维方法。BSO算法将头脑风暴法的不同阶段抽象为聚类、变异、生成新个体、选择四种操作的不断迭代过程,能够跳出局部极值,快速定位优化问题的最优解。BSO已经在许多优化问题中取得了成功,算法流程如下。
在优化问题的定义域内随机产生n个个体组成的种群,每个个体都是d维空间的一个向量,第i个个体表示为:
Xi=(xi1,xi2,…,xid);i=1,2,…,n
(9)
个体初始化后开始1)~5)的迭代过程,每轮迭代过程中生成n个新个体。
1)种群聚类:种群的个体采用k-means聚类为m个子群,根据适应度函数对个体进行排序,每个子群中适应度值最好的定义为中心个体,其余为一般个体;
2)个体变异:随机产生一个[0,1]的随机数p11,若大于预先设定的概率参数p1,随机选中一个子群的中心个体,替换为随机生成的新个体;
3)生成新个体:预先设定概率p2,随机生成[0,1]之间的随机数p2i,与p2进行比较,并通过以下两种方式产生候选个体:
①如果p2i≥p2,随机选中一个子群,选择子群中心个体或随机选择一个一般个体,作为候选个体Xs;
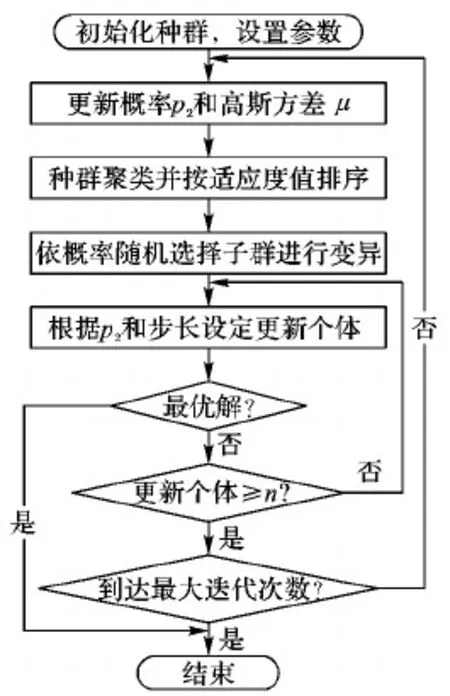
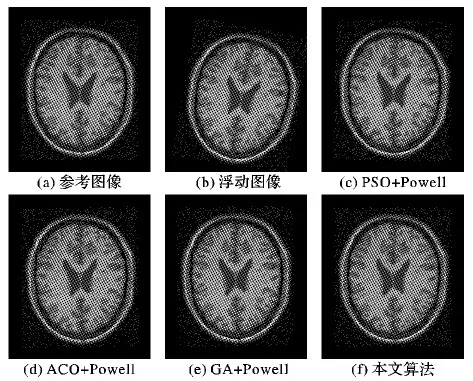
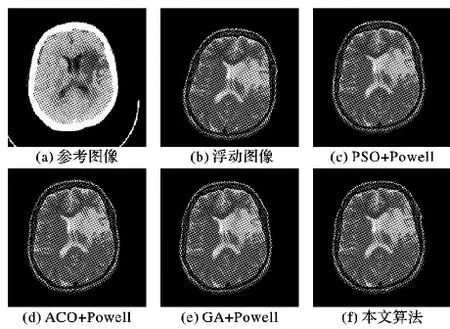
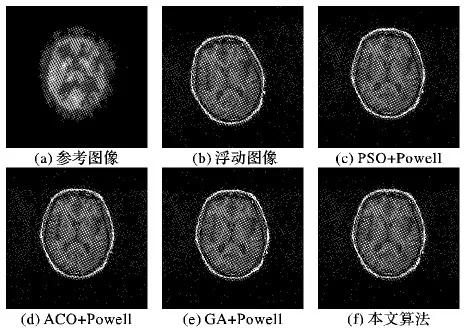
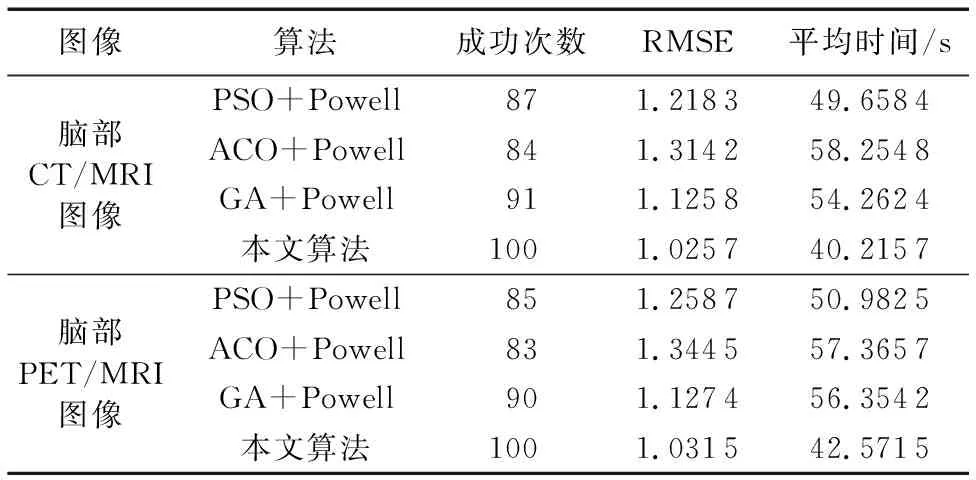
②如果p2i Xs=ω×Xs1+(1-ω)×Xs2 (10) 候选个体Xs加上高斯随机扰动生成新个体Y,如式(11)和(12)所示: Y=Xs+ξ×N(μ,σ) (11) ξ=logsig((0.5×Tmax-t)/S)×rand(0,1) (12) 其中,t为当前迭代次数,Tmax是最大迭代次数,N(μ,σ)是中心在μ方差为σ的高斯随机函数,ξ为对数S变换函数; 4)个体选择:新个体Y的适应度与当前需要更新的个体进行比较,适应度好的个体进入下一代,n个个体全部更新完后转5),否则转3)进行个体更新; 5)若个体达到最优解条件或达到预先设定的迭代次数时,算法结束,否则转1)开始新的迭代过程。 由BSO算法迭代过程可以看出,算法新个体生成方式和步长是算法收敛速度关键因素。MBSO从两个方面进行改进:一是调节新个体生成方式,二是生成新个体过程中的步长调节方法。 在BSO算法迭代过程3)生成新个体时:①中选择一个子群的中心或一般个体作为候选个体Xs,称由此候选个体加随机扰动生成新个体的方式为a方式;②中选择两个子群中心或两个一般个体融合产生新个体作为候选个体Xs,称由此候选个体加随机扰动生成新个体的方式为b方式。分析可知:b方式生成的个体大概率出现在两个子群的中间,适合于搜索初期进行大范围的全局搜索,使算法快速收敛至全局极值区域;a方式生成的新个体大概率出现在候选个体的附近,适合于后期局部细致搜索定位极值点。因此,通过调节每轮迭代过程中b和a方式生成新个体的比例来控制算法全局和局部搜索的能力,前期以b方式生成新个体为主加强全局搜索,后期以a方式生成新个体为主加强局部细致搜索。通过调节概率参数p2可以达到此目的,改进后的概率参数p2变化形式如下: p2=k×p20 (13) k=exp(-α(t/Tmax)β) (14) 其中:p20表示初始概率参数,k是更新因子,t为当前迭代次数,Tmax是最大迭代次数,α和β是正整数。 式(12)中,ξ的两个分量logsig函数和rand函数取值都在(0,1),乘以均值为0、方差为1的高斯随机函数后,取值范围为[-4,4]。logsig函数在Tmax/2处存在一个阶跃,且高斯函数特点决定取值均值附近概率较大。这些因素导致步长与算法所处阶段不匹配,造成算法前期收敛较慢,而后期在极值附近反复震荡,无法快速收敛。因此,可以调节高斯随机函数的方差以调节算法的搜索步长,改进后高斯函数方差变化形式为: σ=kσ0 (15) 其中:σ0为高斯函数初始方差,k取值与式(14)一致。MBSO算法流程如图1所示。 图1 MBSO算法流程 医学图像配准的研究目标是要寻找一种精度高、鲁棒性强、速度快、计算代价较小的优化算法,通过算法寻找配准参数将两幅图像在空间上严格对应起来。MBSO算法对起始点没有要求,具有极强的鲁棒性,能够快速定位全局最优的粗略位置,但是算法复杂度、高收敛缓慢。Powell算法具有极强的局部搜索能力且收敛速度快,但是依赖于初始点的选择,易陷入局部极值。本文在对图像进行小波分解的基础上,将MBSO的全局寻优能力和Powell算法的局部搜索能力结合起来,采用二者的混合优化算法实现图像配准任务。对原始图像进行三层小波分解后,在低分辨率层采用MBSO算法进行全局搜索,此时由于图像较小可以快速确定全局最优值的大概位置,接下来将MBSO算法的优化结果作为初始点,在第2层和原始图像层采用Powell算法进行局部细致搜索,Powell算法的局部搜索能力可以快速定位全局最优的位置。多分辨率的加入可以有效加快MBSO算法的搜索速度,MBSO算法的搜索结果作为Powell算法的初始值,可以有效防止Powell算法陷入局部极值中。算法的具体步骤如下。 1)对于参考图像R和浮动图像F进行三层小波分解,原始图像作为第1层图像,小波分解第2、3层近似系数作为第2、3层图像。原始图像的配准可以转化为第2、3层图像的配准问题,相邻两层平移、旋转参数关系为:低分辨率层图像平移参数为(tx,ty)时,前一层图像平移参数为(2tx,2ty),而旋转角度参数θ保持不变。 2)利用MBSO算法对第3层图像进行配准,将两幅图像的归一化互信息(Normalized Mutual Information, NMI)作为适应度函数,图像灰度直方图灰度区间设置为128,采用最近邻法作为插值方法,在低分辨率层采用这样设置有助于提高搜索速度而不影响搜索的精度。MBSO算法搜索结束后,输出最优配准参数。 3)将步骤2)中MBSO算法得到的配准参数作为Powell算法搜索的起始点在第2层继续搜索。Powell算法的迭代次数设为200,初始步长设为1,允许误差设为0.001,图像灰度直方图灰度区间设置为256,采用部分体积(Partial Volume, PV)插值方法,算法结束时输出本层最优配准参数。 4)将步骤3)得到的最优配准参数作为Powell算法的初始点,重复步骤3在原始图像层进行搜索,得到最优图像配准参数(tx,ty,θ)。 5)用步骤4)得到的配准参数(tx,ty,θ)对浮动图像F进行空间变换,使之与参考图像完全对应起来,完成图像配准过程。 步骤2)中在第3层采用MBSO搜索的流程如下: ①算法初始化:在解空间随机生成均匀分布的50个个体组成初始种群,个体形为(tx,ty,θ),算法最大迭代次数设为200,算法终止适应度阈值设为0.95,预设概率p1为0.5,p20初始设置为0.85,高斯函数参数均值μ设置为0,初始方差σ0设置为3,更新因子k的参数α设置为3,β设置为2,当前迭代代数t为1,用个体对浮动图像进行变换,计算参考和浮动图像的NMI作为个体适应度值。 ②采用k-means将种群聚类为m个子群,对个体按适应度值排序并确定子群中心个体。 ③依概率选中任一子群,用随机生成的个体替换该子群中心个体。根据当前迭代次数计算概率参数p2和高斯函数方差σ。 ④随机生成[0,1]的随机数p2i,如果p2i>p2,则按照a方式选择一个子群中个体作为候选个体Xs,否则按照b方式选择两个子群中个体融合作为候选个体Xs,候选个体加上随机扰动生成新个体Y。 ⑤用新个体Y对浮动图像进行变换后,计算参考和浮动图像的NMI作为Y适应度值,若该值小于待更新个体X的适应度值,将Y舍弃,否则用Y替换X。如果当前最大适应度值大于阈值0.95,则转⑦输出结果,如果50个个体全部更新完毕,转⑥,否则转④生成新个体。 ⑥如果已经达到最大迭代次数,则转⑦,否则转②开始新一轮迭代。 ⑦终止MBSO算法搜索过程,将当前最优适应度函数值的个体作为结果输出。 为了验证本文配准算法的性能,采用加拿大McGill大学BrainWeb数据库[15]的模拟脑MRI图像,以及哈佛大学医学院的脑部数据[16]分别进行单模和多模图像配准实验。实验平台选用Windows操作系统下的Matlab R2012B科学计算软件,硬件配置为Intel Core i3-4170 CPU 3.70 GHz、内存4.00 GB。配准效果可以从定性和定量分析[17-18]两个方面进行评价,本文采用目测效果进行定性评价,采用配准成功次数、精准度和配准时间三个指标对算法进行定量评价。采用均方根误差(Root Mean Square Error, RMSE)作为精度的度量,RMSE值越小则图像配准效果越好。 选择文献[10-11,13]中配准算法作为对比算法,与本文算法进行比较。三种算法分别是粒子群优化(PSO)算法、蚁群优化(ACO)算法和遗传算法(GA)与Powell算法结合的混合算法,以下记三种算法为PSO+Powell、ACO+Powell和GA+Powell。ACO算法、GA、PSO算法种群个体数量设置为50,最大迭代次数设置为200,算法其他参数与文献[10-11,13]中保持一致。Powell算法的迭代次数设为200,初始迭代步长设为1,允许误差设为0.001。 选取BrianWeb数据库中MRI-T1脑部横断面图像进行单模图像配准实验。如图2所示,图2(a)是MRI图像,作为参考图像R,图2(b)将R分别沿水平、竖直方向平移10个和8个像素,绕中心旋转10°,得到浮动图像F,图2(c)~(f)分别是PSO+Powell、ACO+Powell、GA+Powell和本文算法的配准结果。 图2 单模脑部图像配准结果 单模图像配准实验的定量分析中,对图2中参考图像R随机施加±20个像素的平移和±20°的旋转,重复进行100次的配准实验,从配准成功次数、配准精度和平均配准时间对算法效果进行评价。每次实验中计算配准变换参数与真实变换参数的绝对差值(Δx,Δy,Δθ),当平移误差小于1个像素、旋转误差小于1°时,称此次配准达到亚像素级,视为配准成功。 表1列出了100次实验中本文算法和对比算法配准成功的次数、平均RMSE和平均配准时间。综合来看,PSO+Powell算法精度在四种算法排在第二,平均运行时间第二短。GA+Powell算法平均运行时间最长,配准成功率排在第二。ACO+Powell算法配准成功率最低,精度也最差,平均运行时间排在第三。本文算法效果最好,相比PSO+Powell、ACO+Powell和GA+Powell算法,平均RMSE分别下降了28.81%、46.15%和38.24%,平均配准时间分别缩短了18.08%、24.38%和27.47%。 表1 单模图像配准实验定量分析 选取哈佛大学医学院的计算机断层扫描/磁共振成像(Computed Tomography/Magnetic Resonance Imaging, CT/MRI)和正电子放射断层成像/磁共振成像(Positron Emission Tomography/Magnetic Resonance Imaging, PET/MRI)图像分别进行多模配准实验。第一组待配准图像选择急性脑卒中患者CT/MRI图像,如图3所示,图3(a)是CT图像作为参考图像,图3(b)是MRI图像作为浮动图像,图3(c)~(f)分别显示了PSO+Powell、ACO+Powell、GA+Powell和本文算法配准结果。第二组图像选择脑部神经胶质瘤患者PET/MRI图像,图4(a)是PET图像作为参考图像,图4(b)是MRI图像作为浮动图像,图4(c)~(f)分别显示了PSO+Powell、ACO+Powell、GA+Powell和本文算法配准结果。 在CT/MRI和PET/MRI配准成功的基础上,对本文算法多模图像配准效果进行定量分析。实验中以MRI图像配准结果为基准,对两组图像中MRI图像分别随机施加±20个像素的平移和±20°的旋转,重复进行100次的配准实验,从配准成功次数、配准精度和平均配准时间对算法效果进行评价。表2列出了CT/MRI、PET/MRI实验中四种算法配准成功的次数、RMSE平均值和平均配准时间。 由表2可以看出,在多模图像配准中,本文算法在四种算法的结果具有最好的配准表现:平均配准时间在四种算法中是最少的,并且具有100%的配准成功率,RMSE值在四种算法中也是最小的。由表2脑部CT/MRI图像的各项指标来看,在CT/MRI配准中,相比PSO+Powell、ACO+Powell和GA+Powell算法,本文算法RMSE分别下降了15.80%、21.95%和8.89%,平均配准时间分别缩短了19.01%、30.97%和25.88%。由表2脑部PET/MRI图像各项指标来看,在PET/MRI配准中,本文算法RMSE分别下降了18.06%、23.28%和8.50%,平均配准时间分别缩短了16.50%、25.79%和26.46%。 单模和多模医学图像配准结果表明,本文算法相对于PSO+Powell、ACO+Powell和GA+Powell算法,平均RMSE分别下降了20.89%、30.46%和18.54%,平均配准时间分别缩短了17.86%、27.05%、26.60%,并且达到了100%的成功率。实验结果说明,本文算法不仅能够有效减少配准的时间,跳出局部极值的干扰,还可以提高配准的成功率和准确率。MBSO算法特有的对于全局和局部搜索的调节机制和对局部细致搜索能力,不仅能在低分辨率层快速定位全局最优解的范围,同时能够将最优解范围尽可能地缩小,为局部搜索算法Powell提供可信赖的初始点。本文方法的配准结果优于PSO算法、ACO算法和GA与Powell算法结合的优化算法的配准结果,能够快速、准确、自动完成图像配准任务。 图3 脑部CT/MRI图像配准结果 图4 脑部PET/MRI多模图像配准结果 图像算法成功次数RMSE平均时间/s脑部CT/MRI图像脑部PET/MRI图像PSO+Powell871.218349.6584ACO+Powell841.314258.2548GA+Powell911.125854.2624本文算法1001.025740.2157PSO+Powell851.258750.9825ACO+Powell831.344557.3657GA+Powell901.127456.3542本文算法1001.031542.5715 针对现有图像配准算法精度较差、易陷入局部极值和收敛速度慢的问题,本文提出了基于多分辨率分析,MBSO算法与Powell算法结合的医学图像配准算法。算法首先对图像进行小波分解,在低分辨率层采用速度快、精度高MBSO算法进行全局搜索,在高分辨率层采用适于局部搜索的Powell算法完成图像配准任务。以归一化互信息为相似性测度,选择粒子群优化算法、蚁群优化算法、遗传算法与Powell算法结合的混合算法作为对比算法,运用BrainWeb模拟脑数据和哈佛大学医学院真实脑图像进行了对比实验,本文算法在配准成功率、配准时间和配准精度上均优于其他三种算法。实验结果表明,本文算法具有很强的鲁棒性,能够快速、准确完成单模和多模医学图像配准任务。2.3 改进头脑风暴算法
3 本文算法
4 实验与分析
4.1 单模图像配准
4.2 多模医学图像配准
5 结语

