基于deep Q-network双足机器人非平整地面行走稳定性控制方法
赵玉婷,韩宝玲,罗庆生
(1.北京理工大学 机械与车辆学院,北京 100081; 2.北京理工大学 机电学院,北京 100081)
0 引言
双足机器人具有和人类相似的形体结构,其双足直立行走的运动方式在现实中具有广泛的应用前景,其行走稳定性控制问题一直是业界的研究重点。如何使双足机器人适应各种地面,进行快速稳定的行走是研究中的关键问题[1]。
目前,仿人机器人的步态规划主要针对理想的平整地面环境,采用离线方式设计出满足特定全局优化要求的步态序列,然后根据规划好的步态序列控制机器人行走。若是机器人行走过程中遇到凸起或凹陷的不平整地面,会使摆动腿末端提前或推迟触地,使腿末端遭遇过大的地面冲击力,导致机器人因姿态扭曲而摔倒。
近年来,国内外许多学者针对双足机器人在非平整地面的行走稳定性问题,国内外许多学者尝试采用离线步态规划与各种步态在线修正算法结合来实现针对实际行走环境的稳定持续行走[2-5]。如文献[2],利用传统的倒立摆模型与零力矩点(Zero Moment Point, ZMP)得到规划步态后实时收集仿人机器人关节上角度传感器信息,根据这些信息解算得到调整身体姿态所需要的数据,把这些数据与预先规划的步态数据作比较,所得误差经过处理后送回控制系统进行在线步态调节控制。文献[3]采用惯性测量单元(Inertial Measurement Unit, IMU)和力敏电阻(Force Sensing Resistor, FSR)等基本传感器,通过对FSR数据进行处理得到归一化零力矩点,用于站立、摆动等简单运动的反馈控制,从IMU数据过滤得到躯干倾斜角数据,并用于在倾斜地面行走的控制。
上述采用传感器反馈控制进行在线修正对算法的实时快速有效解算有较高要求,尤其在实际环境中由于复杂环境参数的影响,机器人实际控制效果不够理想。而机器学习算法的出现和发展为克服双足机器人复杂控制问题提供了新的方向,在机器人领域得到了越来越广泛的应用。文献[6-8]基于强化学习算法,将其运用在机器人运动控制方面,达到了很好的控制效果。例如文献[6]和文献[7],运用强化学习算法使移动机器人以高维视觉信息作为输入数据来学习获得诸如避开墙壁和沿着中心线移动的良好行为。文献[8]采用深度强化学习方法,将机器人学习扩展到复杂的3D操作任务(如开门)。
本文将强化学习与神经网络结合的Deep Q-Network(DQN)算法[9]应用于双足机器人步态控制,以解决机器人在非平整地面行走时的稳定性问题。该算法无需建立机器人复杂的动力学模型,结合强化学习和神经网络的优势,以离线规划的机器人行走步态为基础,利用DQN算法对双足机器人的步态进行调整。DQN算法以机器人机身在单腿站立相偏离规划位置的距离为状态,机身位置的调整为行动,并利用机身姿态信息来构建奖励函数,可有效改善机器人在非平整地面行走时的稳定性。该方法既避免了传统控制方法需要对机器人进行复杂的动力学建模,又能获得较为良好的控制效果。
1 双足机器人离线步态的生成
双足机器人的步行模型可分为静态步行模型和动态步行模型[10],本文研究仿人机器人在低速、准静态情况下的步行稳定性控制。首先建立双足机器人的运动学模型,并将机器人的上半身视为一个质点,质量集中于机器人的质心位置O0。仿人机器人躯干及下肢共有6个自由度,分别是髋关节3个自由度,膝关节1个自由度,踝关节2个自由度。以仿人机器人的质心作为基础坐标系,以右腿作为研究对象,建立相应的D-H(Denavit-Hartenberg)坐标系如图1所示。其中OXYZ为世界坐标系,O0X0Y0Z0为机身坐标系,XRYRZR为右腿基础坐标系,并依次建立各关节坐标系。其次,基于D-H坐标系建立机器人运动学模型,通过逆运动学求解,建立机器人足端轨迹与关节转角的关系[11]。表1为机器人步行参数,利用复合摆线和三次多项式曲线分别对质心轨迹与足端轨迹进行规划,从而得到离线步态序列[12]。

图1 机器人D-H坐标系

参数值参数值步行周期T2s单腿支撑期Ts0.6s步长S030mm双腿支撑期Tw0.4s步高H08mm
2 非平整地面步态控制算法
2.1 DQN算法
DQN算法是基于强化学习经典算法中Q-学习算法的改进,Q-学习算法是一种不依赖于模型的强化学习算法[13],该算法在迭代学习时采用“状态-动作对”的奖励和Q(S,A)作为估计函数,最优策略为在状态下选用使奖励值最大的行为。算法基本形式为:

(1)
其中:Q(St,At)为Agent在状态St采取动作At获得的奖励折扣和;α为学习率(或学习步长),反映误差被学习的程度;γ是对未来奖励的衰减值,表示未来的奖励对现在的影响。通过贪心策略选择动作,直到值函数收敛,得到最优策略:

(2)
这样即可为每一个状态找到最好的动作,但是对于机器人控制问题,往往其状态空间是高维的,如果逐一计算和存储状态-动作值,容易产生维度灾难。为解决该问题,DQN算法用值函数近似的方法得到Q值[14],即:
Q(s,a)=f(s,a)
(3)
式(3)中的函数关系指的是通过神经网络学习,得到Q值与状态及动作之间函数映射关系。神经网络采用两个结构相同、参数不同的全连接神经网络:“当前值”网络和“目标值”网络,训练过程中对当前Q值与目标Q值分别更新,并以两者差值的平方作为损失函数进行反向传递。算法流程如图2所示。

图2 DQN算法流程
对于高维状态空间,DQN算法只把状态S作为输入,而输出一个矩阵,[Q(s1,a1),Q(s2,a2),…,Q(sn,an)]这个矩阵是在当前状态下所有可能采取的动作所对应的奖惩值,通过经验学习,建立状态S与该矩阵之间的映射关系,然后从中选择最优的动作,其实现过程如DQN算法伪代码所示。
DQN算法。
输入:环境E;动作空间A;起始状态x0;状态空间S;奖赏折扣γ;更新步长α。
过程:
1)
初始化回放存储空间D并定义容量大小N;
2)
使用随机权重θ初始化动作-价值函数Q;
3)

4)
循环(对每一个episode):
5)
初始化状态序列s1={x1}φ1=φ(s1)
6)
循环(对episode中的每一步):
7)
选择一个动作a:
8)
以概率ε选择一个随机动作at
9)
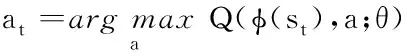
10)
在仿真器中执行动作at并观察奖励rt和新状态xt+1;
11)
令st+1=st,at,xt+1并进行预处理使φt+1=φ(st+1);
12)
在回放存储空间D中保存经验(φt,at,rt,φt+1);
13)
从D中随机选取小批样本(φj,aj,rj,φj+1);
14)

15)
对于θ使用损失函数(yi-Q(φj,aj;θ))2梯度下降更新;
16)

17)
判断终止条件,结束循环
18)
判断终止条件,结束循环
输出:当前状态下所有可能采取的动作所对应的Q值。
2.2 算法实现
2.2.1 机器人状态空间
选取机器人姿态信息中能够直观反映机器人是否稳定的信息作为状态S,也就是每一采样时刻x-y平面绕机身坐标系Z0轴的角度θxy和x-z平面绕机身坐标系Y0轴的角度θxz。因此DQN算法的状态空间S={θxy,θxz},状态值st(st∈S)。
2.2.2 机器人动作空间
仿人机器人运动采用“一走一停”的策略,即在单相支撑时进行摆动腿的迈腿动作,在双腿支撑相,进行质心调整,保证机器人的质心始终在稳定支撑区内。离线步态适用于平地行走,机器人处于单腿支撑相时质心在地面上的投影位于支撑脚掌的中心,但在将该步态应用于复杂地形时,机器人质心位置会发生变化,为使机器人稳定,需要对机身位置进行调整。因此,将动作离散为在前后、左右方向上质心的调整值,本文使用的仿人机器人平台脚掌的大小为100 mm×60 mm,设定的步长s0为30 mm,将质心调整的距离设定为0 mm、5 mm、10 mm和15 mm四个值;质心调整方向分别为Z0轴方向和Y0轴方向,在每个轴向又分正、负两个方向,即{±Z0,±Y0};因此在每一步动作调整的过程中动作值空间A的大小为4×4×4=64,步态的调整动作记为a(a∈A)。
2.2.3 奖惩机制
在对DQN算法的奖惩值函数进行设计时,以仿人机器人进行调整之后是否摔倒作为最终的评价。机器人摔倒得到的奖励值为-10,稳定行走未摔倒得到的奖励值为50。
(4)
其中:规定当θxy≥60°或θxz≥60°时判定为机器人摔倒,其他情况均记为正奖励。
2.2.4 步行控制器学习过程
以上对DQN算法的状态值、动作值、奖惩值函数和网络结构进行了设计。机器人每走一步都会对DQN算法中的网络结构参数和机器人的质心坐标进行更新。结合对机器人的步态规划和姿态传感器的反馈信息,通过设计的DQN算法结构训练分析,不断与环境进行交互学习,得出质心调整和机器人姿态信息之间的关系。学习过程如图3所示。
3 仿真验证与结果分析
3.1 仿真环境
本文使用V-Rep作为仿真环境,使用双足机器人Asti模型,在机器人的行进方向随机分布了厚度为4 mm、大小为10 mm×10 mm的障碍物,模拟“非平整地面”,场景如图4所示。以离线步态为基础步态,将其导入到V-Rep构建的机器人的“Path”内,通过vrep_ros_bridge构建ROS和V-Rep的联合仿真,运行DQN运算节点;输出相应的动作指令给控制器,对基础步态进行实时的调整,机器人每摔倒一次或者机器人顺利到达终点记为一个回合。

图3 步行控制器学习过程

图4 仿真环境
3.2 算法参数设计
算法参数的调整对学习效果和效率起到重要的作用,其中学习率α(更新步长)体现值函数到达最优值的速度快慢程度:学习速率太小,则会使效率过低,收敛过慢;如果学习速率太大,则会导致代价函数振荡,错过最优值,无法收敛。经实验,本文选择学习率为0.001。
奖惩折扣因子γ取值在[0,1],学习效果不仅需要考虑当下的回报,还要考虑未来的回报,距离当前时间越近的奖励,考虑的程度越高,经实验,本文将折扣因子设置为0.9。
ε-贪心法以ε的概率随机选择一个动作,以1-ε的概率选择当前最优的动作。只需记录每个动作的当前平均奖励值与被选中的次数,便可以增量式更新。ε一般取值较小,本文取值为0.01。
如前文所述,记忆库存储历史经验,每次DQN更新的时候,可以随机抽取历史经验进行学习。随机抽样的方法可以降低不同历史经验之间的相关性,以提高神经网络的更新效率。根据经验尝试以及硬件要求,选取记忆库参数如表2所示。

表2 DQN算法相关参数
3.3 仿真训练过程
为验证本算法的有效性,针对行走中的典型情况,作了以下三种情况的仿真:1)机器人在平整地面行走,由于未遇到不平整地面障碍物,依靠离线规划的步态行走;2)中途遇到不平整地面且不加DQN算法控制,障碍物厚度为3 mm;3)中途遇到不平整地面使用DQN算法控制,障碍物与2)中完全相同;记录三种仿真情况下行走过程姿态角变化。
如图5所示,A1~A4是未使用DQN算法时,机器人在不平整地面的行走情况。A1为机器人的初始状态;A2显示在机器人未碰到障碍物时,能够正常行走;A3~A4显示机器人由于没有进行质心位置的调整,发生摔倒。随后,使用DQN算法进行姿态调整,对机器人进行了360个回合(机器人摔倒或顺利到达终点记为一个回合)的训练测试,最终训练结果即B1~B4所示,B1为初始状态,机器人基本学会了质心调整和机器人姿态角度之间的关系,能稳定行走到终点。

图5 仿真结果关键帧对比
3.4 结果分析
图6和图7分别为机器人行走过程中左右方向和前后方向的姿态角,两图中的(a)图均为三种仿真情况的数据,(b)图均为“平整地面”和“非平整地面使用强化学习算法”两种情况的对比。

图6 机器人左右姿态角数据曲线
从图6和图7可知,在平整地面上行走,机器人左右姿态角度α波动范围在2°以内,前后姿态角度β波动范围在0.5°以内;当行走过程遇到不平整地面,在未使用DQN算法进行姿态调整的情况下,左右姿态角发生90°左右的波动,前后姿态角发生10°~20°的变化,机器人发生摔倒;当经过DQN算法进行学习之后,机器人在遇到非平整地面后,虽然角度有所波动,但是波动范围大部分在2°以内,极个别位置有3°左右的波动,该波动范围与文献[4]采用ZMP控制在不平整路面姿态角波动范围2°以内相比,均在可接受范围内,说明双足机器人使用DQN算法能够通过质心位置的调整实现在不平整路面上的稳定行走。

图7 机器人前后姿态角数据曲线
经过360回合将近10 000步的训练后,得到DQN算法的损失函数和奖励值函数的数据,图8表示的是整个训练过程中损失函数的变化,可以看出损失函数随着训练步数的增加逐渐减小,趋于稳定。

图8 误差变化曲线
通过对以上仿真结果和实验数据的分析可知,DQN算法的损失函数最终收敛,累积奖励收敛于稳定值,这说明基于DQN算法的步行控制器逐渐习得调整机器人质心的正确方式,从而使机器人在非平整地面保持稳定行走。
4 结语
本文针对双足机器人在非平整地面行走时容易失去运动稳定性的问题,提出了基于强化学习的双足机器人步态控制新方法,主要包括两部分:1)离线步态的生成;2)基于强化学习DQN算法的步态调整算法。在V-Rep环境下搭建了不平整地面仿真环境,仿真结果显示机器人在遇到非平整地面后,经过算法调整后姿态角度波动范围大部分在2°以内,极个别位置有3°左右的波动,表明机器人学会了步态自主调整,能够保持行走稳定性,由此证明了算法的有效性,与传统控制方法相比,无需进行复杂的动力学建模过程,为解决双足机器人在非平整地面行走的稳定性问题提供了新的思路。

