基于剪切破坏的深长隧道掌子面隔水岩层安全厚度的研究
夏沅谱,董 鑫,2, 熊自明,卢 浩,柯夏瑶
(1. 陆军工程大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007;2.中国人民解放军61172部队,北京 102204;3.南昌大学公共管理学院,江西 南昌 330031)
在地质复杂区域如岩溶发育、断层、破碎带、暗河等地区修建隧道容易引发塌方[1]、突涌水[2]等地质灾害。一旦施工期间引发地质灾害,则可能造成经济损失、工期延误、成本超支、环境破坏甚至人员伤亡等不利影响[3~5]。因此,如何安全顺利施工一直是岩土工程界面临的主要挑战之一[6~7]。随着在地质复杂区域修建的隧道日益增多,突涌水造成的损失已经超过其他类型的地质灾害[8~9]。经过相关统计分析,由于爆破、卸荷及高水压等不利因素的影响,隧道掌子面附近区域属于突涌水灾害发生频率相对较高的区域[10]。因此,掌子面前方防突涌水安全厚度的研究对控制突涌水风险、减轻灾害后果等都有积极的作用。
当前,关于深长隧道隔水岩层安全厚度的研究日益受到重视,相继建立了各种计算模型。例如,干昆蓉等[11]认为防突岩墙厚度的确定需考虑爆破对围岩的扰动和振动影响、开挖卸荷对围岩松弛影响、高压水及地应力的作用,根据施工经验提出安全厚度的确定方法。曹茜[12]以宜万铁路工程为研究对象,利用FLAC3D数值软件对隧道与周围隐伏溶洞的安全距离进行了模拟分析。徐光黎等[13]利用三维有限元方法模拟岩溶隧道开挖过程,基于非线性回归法,提出了能简单快速预测掌子面前方隔水岩盘安全厚度的数学模型。刘超群等[14]通过数值模拟和理论计算,对隧道掌子面与溶洞安全距离的影响因素进行了分析研究,建立了预测隧道掌子面前方岩盘安全厚度的计算模型。此外,张志诚等[15]、李浪等[16]为了研究在不同地应力、围岩类型以及水压下隧道突水时的最小安全岩层厚度问题,研制了一种用于模拟突水灾害的模型试验系统,开展了相关模型实验,并与数值模拟和理论分析结果进行了对比分析。但由于时间、成本等因素的影响无法开展大量的模型实验研究。
数值模拟和模型实验是对理论分析结果的验证,力学理论分析是深长隧道防突安全厚度研究的基础。李利平等[17]将发生裂隙突水的岩溶隧道岩墙厚度范围分为围岩松弛区、安全厚度区和裂隙带区 3 段,并分别推导了其半解析表达式。郭佳奇等[18]在文献[15]的基础上进一步把岩墙安全厚度分为抗裂区Sf和裂隙带Sc两部分。孙谋等[19]、李集等[20]认为防突岩体由于强度不够发生整体破断突水,并基于能量守恒法则和突变理论提出了突水时的最小安全厚度估算公式。基于断裂力学的力学分析过于复杂,不利于工程应用,因此,一些学者如郭佳奇[21]利用Mohr-Coulomb准则表达简单、意义明确且参数容易获得的特点,构建了基于剪切破坏机理的掌子面前方隔水岩层安全厚度力学分析模型。翟友成等[22]认为文献[21]提出的计算模型在剪切面法向应力的确定、开挖卸荷对围岩初始应力的影响以及岩土体物理力学参数不确定性等方面的处理都存在不足,提出了初步的改进措施,但其研究过程仍然有待改进,例如,剪切破坏面的选取与基本力学模型不符。杨子汉等[23]基于上限原理和Mohr-Coulomb破坏准则构建了岩溶隧道岩墙厚度计算公式,但并未考虑地应力对内能耗散的影响。
本文主要基于Mohr-Coulomb剪切破坏准则,通过分析现有研究成果存在的问题,提出相应的解决方法,继而构建隧道掌子面前方隔水岩层安全厚度计算模型,分析各因素与隔水岩层安全厚度间的关系以及合适处理模型参数的不确定性问题。通过对隧道突水失稳破坏的力学分析、不确定性处理等的研究,可以更全面地掌握隧道突水过程的特点,采取有效的预防措施,对隧道安全施工、减少灾害损失有积极的意义。
1 隔水岩层安全厚度的确定
1.1 隧道突水隔水岩层剪切破坏分析
在高地应力条件下,隧道掌子面前方隔水岩层的岩石破坏模式可以看作剪切破坏。将突水时的隧道掌子面与含水体的距离定义为隔水岩层的最小安全厚度(图1)。文献[21~22]基于摩尔-库伦破坏准则针对隔水岩层剪切破坏模式进行了研究,并构建了抗剪切破坏模型(图2)。但实际中岩石剪切破坏面角度更可能是45°+φ/2或45°-φ/2,水平方向的极限剪切应力的破坏很难发生。为此,本文重新构建了隔水岩层剪切破坏力学分析模型。
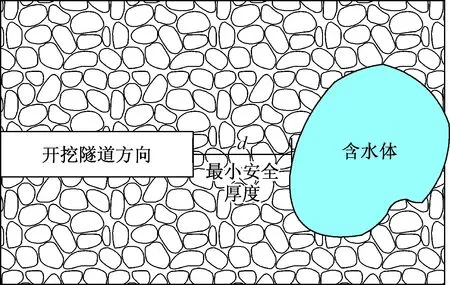
图1 隧道开挖掌子面突水最小安全厚度示意图Fig.1 Schematic diagram showing the minimum safe thickness of water inrush during tunneling
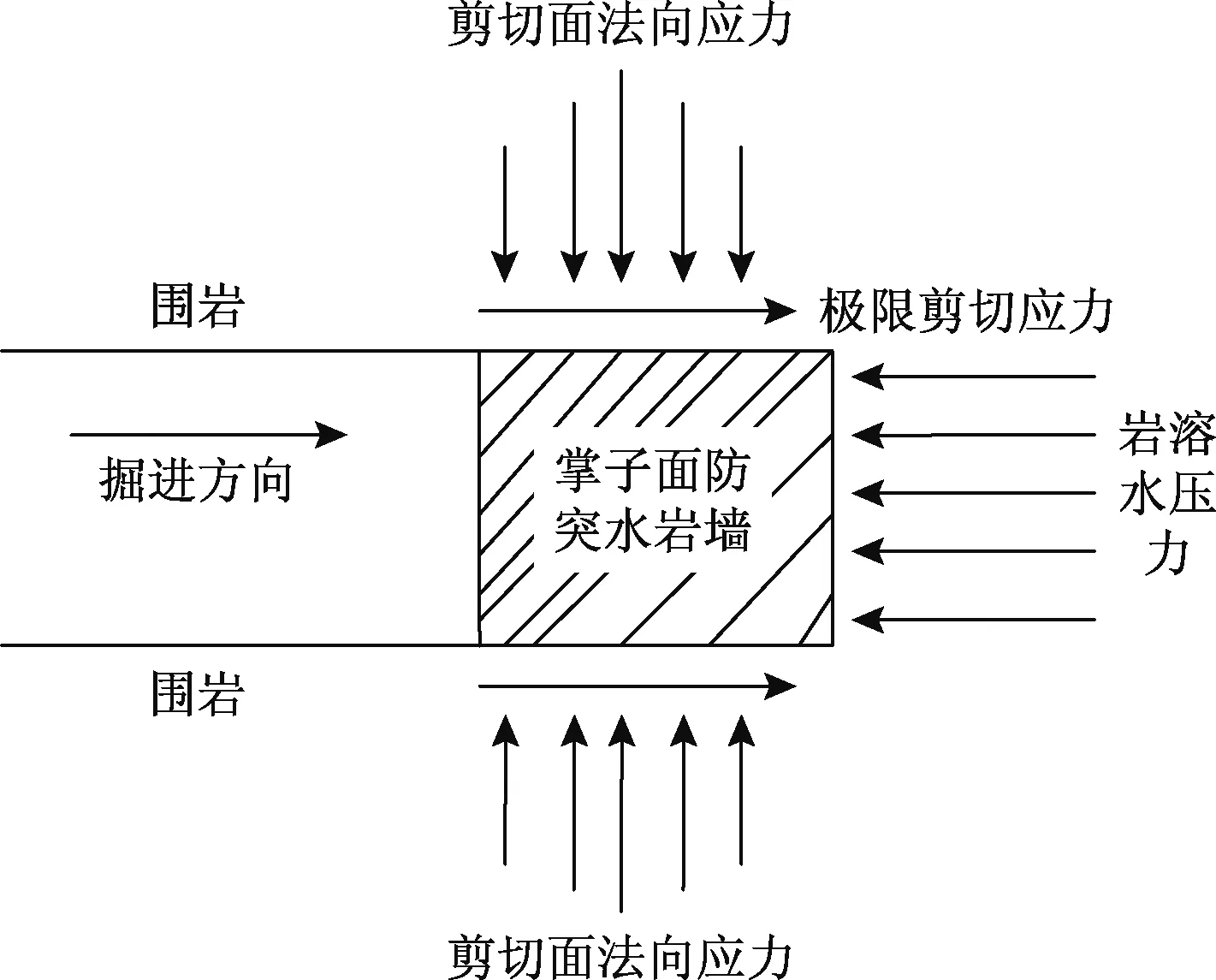
图2 隧道掌子面抗剪切力学模型Fig.2 Mechanics model of shear resistance in the tunnel face
从宏观力学角度分析,隧道突水是由于溶腔水压突破隔水岩层的屏障,也即水压力大于岩层的阻力导致隔水岩层变形破坏。可用极限状态方程表示:
U=S-Q
(1)
式中:Q——促使岩层变形破坏直至突水的外力或主动力,即水压力;
S——阻碍岩层变形破坏的被动力或阻力,主要由剪切破坏滑移面的黏聚力和内摩擦力提供。
随着隧道掌子面不断向前推进,外力Q与抗力S会发生变化(图3)。从图3可知,随着隧道的开挖,当隧道开挖与高压富水体的距离为L=RcotФ时,隔水岩层沿剪切滑移面开始受外力作用,此时主动力Q=0。如果继续开挖掘进,则水体与剪切破坏体的接触面积在增大,而剪切滑移面的接触面积在减小,也即主动力Q会逐渐增大,而抗力S会逐渐减小。建立隧道突水隔水岩层力学分析示意图(图4)。

图3 隔水岩层初始示意图Fig.3 Initial schematic diagram of the aquifuge

图4 随开挖距离的受力分析Fig.4 Force analysis with the excavation distance
Q=p·π·r2=p·π·(dtanΦ)2
(2)
抗剪强度τ=σcosφ+c,则可得到滑移面上的摩阻力为:
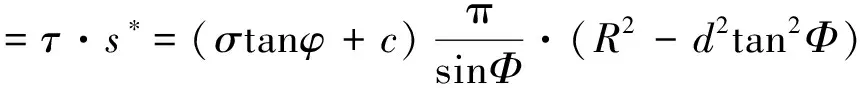
(3)
式中:σ——作用在剪切破坏面上的正应力;
c——黏聚力;
s*——岩体滑移面的接触面积。
F阻在水平方向上的分量便为抗力S,即S=F阻·cosФ。临界状态即U=(S-Q)=0,则有:
p·π·(dtanΦ)2=π(σtanφ+c)(R2cotΦ-d2tanΦ)
(4)
由式(4)可得:
(5)
由图4的几何关系可知,临界隔水岩层厚度为:
(6)
由于Ф=45°+φ/2,式(6)可以进一步简化为:

(7)
从公式中可以看出,隔水岩层临界安全厚度与剪切破坏面法向应力σ、隧道开挖半径R、黏聚力c、内摩擦角φ、水压p等因素有关。在实际工程中由于隧道爆破开挖扰动以及卸荷等的影响,导致剪切面上的σ和c应该呈逐渐减小的趋势。因此,实际中临界厚度会比上述公式计算的值要大。
1.2 考虑开挖卸荷影响的剪切破坏面法向应力分析
根据摩尔-库伦强度准则,临界隔水岩层厚度受到剪切面法向应力σn的影响。当前多数文献并未详细分析剪切面法向应力的变化对安全厚度的影响。但对于深部隧道,初始地应力、开挖卸荷等因素对剪切面法向应力的影响不能忽视。本节在翟友成等[22]研究成果的基础上,对剪切面法向应力的确定做进一步的分析。
1.2.1初始地应力场对剪切破坏面法向应力的影响
地应力由竖向应力和水平应力构成,只考虑自重应力场时,假设埋深为H,竖向应力为σv=γH,水平应力为σH=λγH,一般情况下侧压力系数λ<1。因此,竖向应力大于水平应力。但大量的实测资料表明,地质构造形态改变了自重应力场的状态,构造应力场对竖向应力影响相对较小,竖向应力仍可按公式λH计算,但对水平向应力影响较为明显[24]。为此,邓祥辉[25]、孙伟亮[26]提出了如下的水平方向的应力计算公式:
σH=(λ+kt)γH=kγH
(8)
式中:kt——构造应力系数;
k——同时考虑自重应力场和构造应力场的岩体侧压力系数。
在实际工程中,可通过水压致裂法、应力解除法、地球物理探测法等精确确定构造应力[27~28]。但通过大量实测数据分析发现,构造应力场中水平应力普遍大于自重应力场的水平应力分量,且经常大于垂直应力分量,也即是式(8)中系数k经常出现k>1的情形[24,29~30]。对于较深部的岩体,系数k一般大于1且随着埋深的增加会趋向于1达到静水状态[31]。
考虑隧道工程突水的危险性,应该选择保守的隔水岩层厚度,即较小的法向应力值:
σ=min(σvcosΦ,σHsinΦ)
(9)
σvcosФ=γHcos(45°+φ/2)
σHsinФ=γHsin(45°+φ/2)
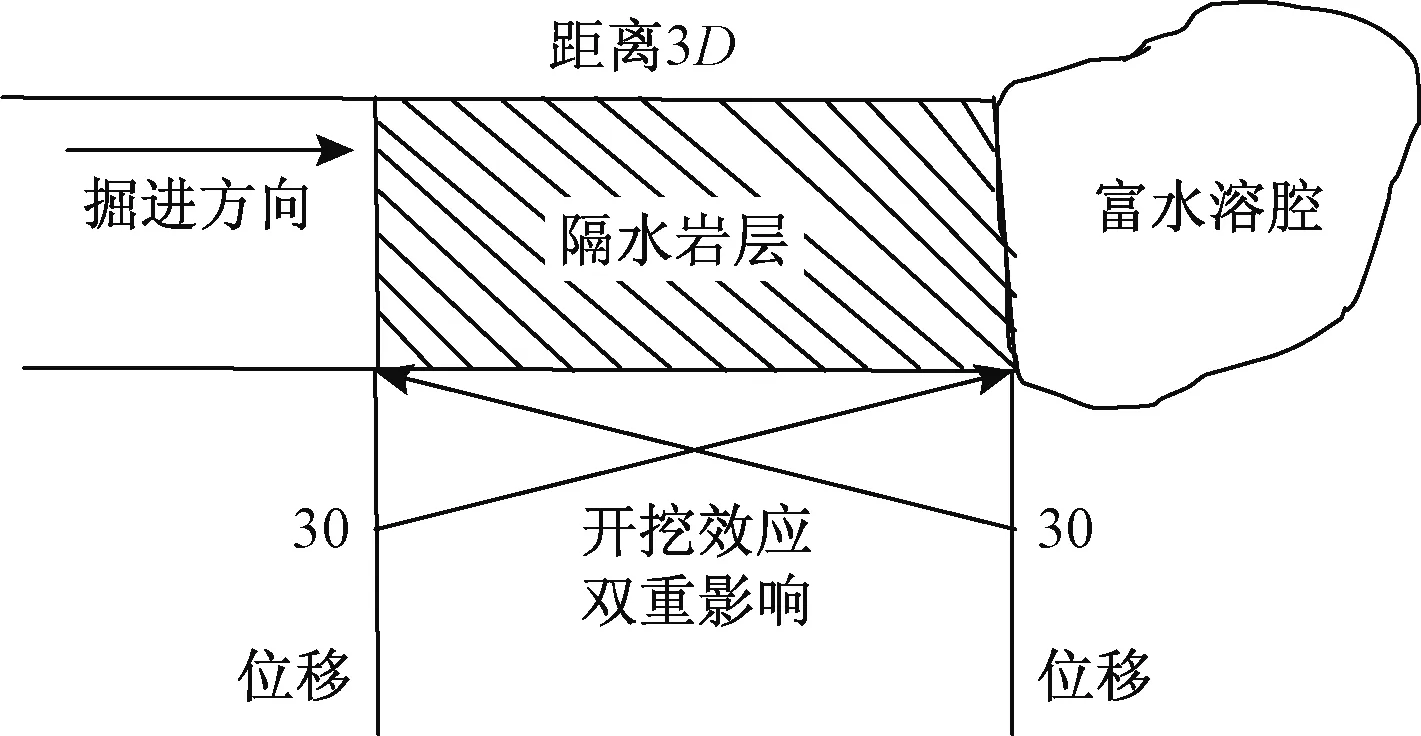
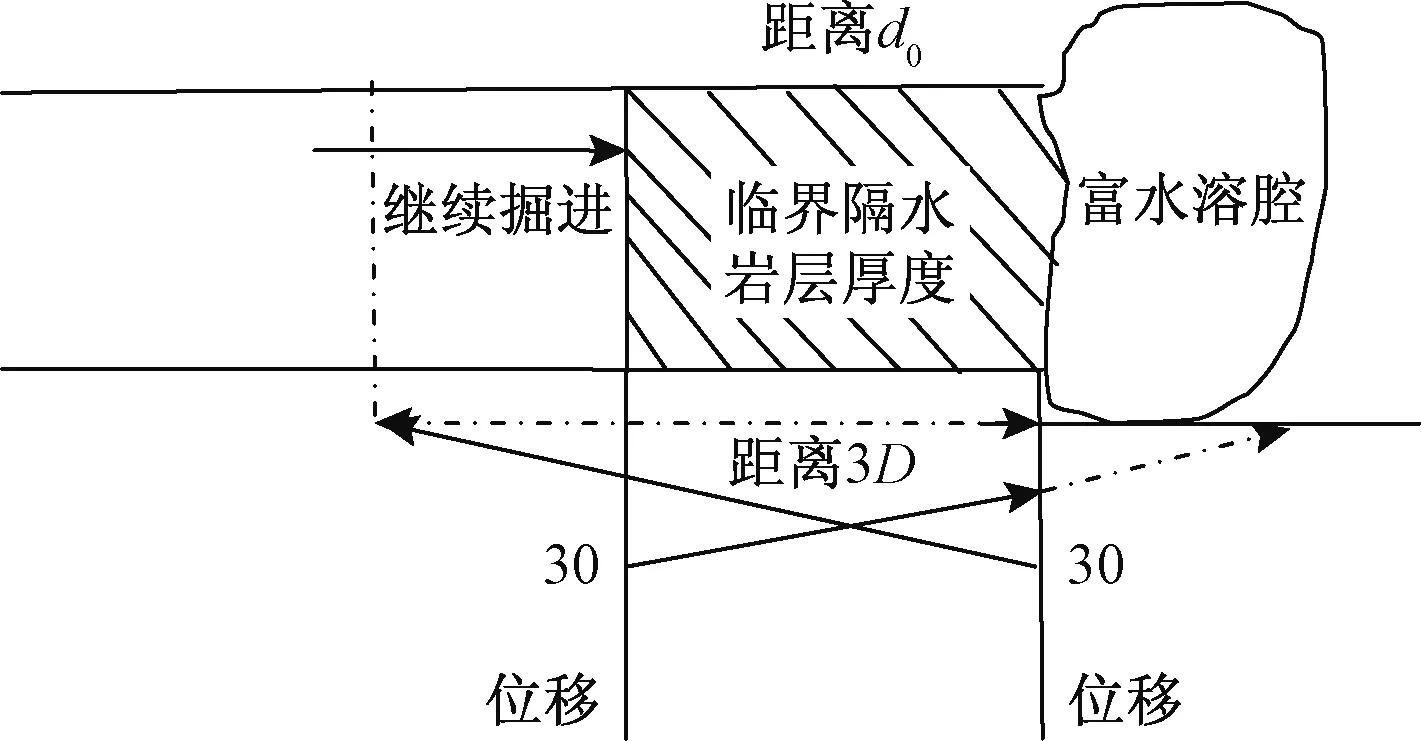
由于内摩擦角0<φ<90°,所以有cos(45°+φ/2) (10) 1.2.2隧道开挖效应对地应力场的影响 隧道开挖会改变原有的初始应力场,使得应力重分布并形成二次应力场。如果隔水岩层安全厚度计算过程中仍然采用原始应力场,则计算结果会与工程实际相差较大,降低应用效果。文献[22]虽然从掌子面和富水溶洞两端同时考虑开挖效应对剪切面法向应力的影响,但在计算受双向影响的法向应力时将会出现问题。本节基于文献[22]已有研究成果,对开挖效应对法向应力的影响进行了重新分析。 隧道开挖效应包括空间效应和时间效应。空间效应是指隧道开挖过程中,由于受到围岩的约束作用,使得沿隧道纵向各断面上的应力释放和位移释放都不相同,且对掌子面前方围岩的影响约为(2~3)倍隧道直径。时间效应指围岩的应力释放和围岩变形不是瞬间完成的,而是随着开挖的逐步推进逐渐完成的,本质上反映的是围岩的流变特性。对于中等坚硬较完整的岩石隧道,未开挖断面轮廓上任一点从受临近开挖断面影响至该断面挖除前该处累积变形量一般占到总变形量的30%[32~33]。由于隧道开挖引起围岩位移和应力的双重变化,因此从位移释放和应力两方面研究开挖效应。对于隔水岩层安全厚度的确定,需要考虑隧道开挖后开挖效应影响范围内各断面的应力分布。关于应力释放问题,直接测量或者理论计算应力释放都比较困难。但由于应力释放和位移释放同时存在,二者间存在紧密联系。杨友彬等[34]、郭瑞等[35]从位移释放与应力释放间的关系入手研究应力释放规律,并发现应力释放和位移释放具有很好的线性相关性。因此,可以根据位移释放规律研究应力释放规律。文献[24]根据大量实测结果及理论分析发现掌子面附近围岩的位移释放分布图5所示。 图5 开挖效应下的位移释放规律示意图Fig.5 Displacement release rules of the excavation effect 由图5可知,开挖会导致掌子面附近不同断面围岩产生不同位移释放,其中掌子面前方3倍洞径距离处的位移变化为零,而掌子面后方3倍洞径处位移完全释放,掌子面处位移释放率为30%。根据位移变化与应力释放间的密切关系,可以假定掌子面处应力释放量为总的30%,前方3D处应力没有变化,而后方3D处应力已经完全释放。同时为了简化计算,可以认为应力沿隧道轴线呈线性变化。此外,文献[19]同时假设富水溶腔一端的应力变化也类似。因此,当隔水岩层厚度为3D时,其开始受到掌子面开挖和富水溶洞的双重影响(图6)。根据理论分析和工程经验,临界隔水岩层厚度一般不超过2倍洞径。因此, 分析时需考虑上述双重影响。 图6 隔水岩层开挖效应双重影响Fig.6 Double effect of excavation effect of the aquifuge 由图6可知,当隔水岩层厚度为3D时,由几何关系可知上述区间任意断面处的位移释放率都为30%,即各断面的位移变化是相同的。当隧道继续掘进直至临界隔水岩层厚度时,各断面位移释放量如图7所示。 由图7易知掌子面处和溶腔端面处的位移释放量为: 图7 临界隔水岩层厚度位移释放分布示意图(%)Fig.7 Displacement distribution diagram of the critical aquifuge thickness (11) (12) 把式(12)代入式(7)中,可得考虑构造应力和开挖效应影响的临界隔水岩层安全厚度计算公式: (13) (14) 通过上述公式可知,考虑开挖效应的剪切破坏面法向应力比式(7)中的明显要小,这与目前多数临界隔水岩层计算公式有显著区别。隔水岩层安全厚度主要受埋深H、黏聚力c、内摩擦角φ、隧道开挖半径R以及水压p的影响。通过简单的因素与安全厚度关系的分析可知,当黏聚力、内摩擦角以及埋深越大时,所需的安全厚度会越小,而当半径越大,水压越大时,所需的安全厚度也越大,这与工程实际情况是相符合的。 跃龙门隧道为成兰线重点控制性隧道之一,采用双线分修,隧道长达20 km,属越岭隧道,穿越涪江水系、多条分水岭,D2K91+020~D2K96+200段水系汇入雎水河,经罗江汇入涪江,D2K96+200~D2K100+000段的水系汇入金溪沟,经安昌河汇入涪江,D2K96+200为雎水河与金溪沟的分水岭,D2K100+000~D2K104+150段水系汇入雎水河,D2K100+000为金溪沟与雎水河的分水岭;D2K104+150~D2K110+994.3段的水系汇入土门河,经湔江汇入涪江, D2K104+150为雎水与土门河的分水岭。跃龙门隧道含可溶岩之灰岩、白云质灰岩、千枚岩、炭质千枚岩夹灰岩、泥灰岩、结晶灰岩、粉砂岩、凝灰岩,突水突泥风险主要集中在龙门山中央断裂—广通坝断层、高川坪倒转向斜、龙门山中央断裂—高川坪活动断层、可溶岩富水段、下穿雎水河段、可溶岩与非可溶岩接触带、大屋基倒转背斜、千佛山1#断层、千佛山断层、老林口倒转复向斜、山腰倒转复背斜、土主庙断层等地质构造带。跃龙门隧道3#斜井位于线路左侧,起点里程桩号为XJ3K0,与正线相接于D2K97+700处,终点里程桩号XJ3K2+30, 3#斜井全长2 030 m,最大埋深872 m。斜井进口位于高川和左岸,洞口标高1 280 m。 2015年3月3日,当隧道开挖掘进到XJ3K0+396时,掌子面出现少量水,呈淋雨状;2015年3月8日,爆破作业后水量突然加大,施工队立即投入抽水设备,叫停洞内施工。2015年3月10日,在掌子面施作超前水平钻(总长38 m),钻至XJ3K0+382处,孔内有大量水涌出,沿钻口喷出2 m,有明显水压;钻至XJ3K0+356处水压太大无法钻进,抽钻杆喷出15 m,最后一节钻杆被水压喷出,水质清澈。2015年3月14日又施作3个钻孔,水量增大,导致洞内被淹70 m,涌水量约为1 000 m3/h。2015年3月14日15点左右,洞内水量未有增长。掌子面有污水泵6台,75 kw(130 m3/h)1台,13 kw(70 m3/h)3台,160 kw(320 m3/h)2台,每小时涌水量800~900 m3。跃龙门隧道3#斜井的涌水量变化曲线如图8所示。 图8 跃龙门隧道3#斜井涌水量趋势图Fig.8 Trend of water inflow in the 3# inclined shaft of the Yuelongmen tunnel 从图8可看出,3#斜井涌水灾害已经影响了施工进度,后续施工发生大规模突水风险较高。为了控制突水风险,防止出现大规模突水事故,必须开展隔水岩层防突厚度研究,为下一步施工提供依据。 掌子面围岩主要为寒武系清平组灰岩,围岩较破碎,岩质硬,节理裂隙局部发育,埋深约800 m。涌水位置工程地质剖面如图9所示。 图9 涌水点位置Fig.9 Location of the water inflow point 由式(14)可知,需确定的参数变量为γ,c,φ,p。其中c,φ值由单轴抗压强度σc、地质力学指标GSI、扰动参数D与岩石参数mi等确定。凝灰岩的容重为2.3~2.5 g/cm3,岩质较硬的凝灰岩饱和单轴抗压强度为40~60 MPa。由于采用光面爆破,因此岩体扰动参数D可取0.7~0.8,凝灰岩岩石参数mi取值范围为8~18。3月21日施作超前地质预报,结果如图10所示。根据预报综合分析结果,XJ3K0+393-385段围压破碎,岩质硬,富水,围岩等级为IV级。由此根据岩体地质强度指标区间表确定GSI的范围为60~70。由于埋深较大,且涌水点位置与地表雎水河有一定的水力联系,因此形成高水头压力,且通过现场超前水平钻量测水压,可以确定水压的取值范围为8~10 MPa。 图10 跃龙门隧道XJ3K0+393-385段超前预报结果Fig.10 Advance prediction results of the XJ3K0+393-385 section of the Yuelongmen tunnel 综上所述,可以确定:γ为[2.3,2.5] g/cm3(也即[23,25]kN/m3),D为[0.7,0.8],mi为[8,18],σc为[40,60],GSI为[40,60]。并通过相关参数转换公式[36]得到岩体c,φ的区间值分别为[0.82,1.63] MPa与[33.5,47.7]°。 (1)基于区间非概率可靠性分析 跃龙门隧道断面半径为5 m,隧道埋深为800 m,p,c,φ,γ为区间变量,其值分别为[8,10]MPa,[0.82,1.63] MPa,[33.5,47.8]°,[23,25]kN/m3。利用式(14)以及区间分析运算法则,临界隔水岩层厚度d0的取值也为区间,并假定为[d0l,d0u]。根据区间非概率可靠性指标的定义[19,35]可知确保隧道不发生突水的条件是d>d0u。可以利用蒙特卡罗随机抽样技术进行计算,但为了得到精确解可能需要反复大量的计算,例如文献[22]进行了200万次的计算才得到精确解。计算d0区间值本质上是约束条件下的非线性函数优化问题,可以利用matlab编程进行优化计算。本文通过编程计算得临界隔水岩层厚度d0区间值为[1.09,1.67]。从可靠性角度考虑确保不发生突水的隔水岩层防突厚度需大于1.67 m。 (2)基于概率的隔水岩层安全厚度的不确定性分析 假设c,φ都属于正态分布,在已知区间范围下,根据3σ原则,可确定二者的概率分布参数取值。水压与容重假定为均匀分布,则随机变量的概率分布如表1所示。利用蒙特卡洛进行仿真模拟,可得临界隔水岩层厚度d0的分布(图11)。 表1 随机变量概率分布Table 1 Probability distribution of random variables 图11 临界隔水岩层厚度d0的分布Fig.11 Thickness distribution of the critical aquifuge 由图11可知,d0的分布类似于正态分布,分布区间大致为[1.2,1.5] m。同时,为了说明计算过程中考虑开挖卸荷对初始应力影响的必要性,把相应的参数变量区间代入式(7)和(10)进行计算,得隔水岩层临界厚度为[0.74,1.2] m。通过对比分析可知,在不考虑开挖卸荷作用时,所计算的临界厚度是偏小的,开挖卸荷的影响是较明显的。为了验证本文所提方法的可靠性,可通过确定现场预留的掌子面距含水体的实际距离进行对比验证。在实际操作中,通常采用超前水平钻、TSP地质雷达、激发极化与瞬变电磁等多种超前地质预报手段进行前方水体的探测。虽然有诸多超前地质预报手段,但仍然难以精确测出前方水体的方位与储量,因此隔水岩层的实际厚度仍然是一个不确定性的值。通过超前地质预报结果分析以及专家工程经验,初步判定掌子面隔水岩层的实际预留厚度为[1.32,1.87] m。通过对比可知基于Mohr-Coulomb破坏准则计算的隔水岩层临界厚度与实际预留厚度还是比较吻合的,这也进一步说明了本文所提方法的合理性。 (1)建立了基于Mohr-Coulomb准则的隔水岩层剪切破坏失稳模型,得到了隔水岩层临界安全厚度的计算表达式,从表达式中可知,隔水岩层临界安全厚度与埋深、隧道开挖半径、黏聚力、内摩擦角与水压都有一定的关系,从影响因素角度考虑与现有的其他表达式基本一致。 (2)考虑了隧道开挖的开挖效应对围岩初始位移和应力的影响,通过分析发现隧道开挖对初始位移和初始应力的影响较显著,剪切破坏时有必要考虑开挖后应力的变化。 (3)工程案例分析中考虑了隧道工程的不确定处理问题,分别利用区间非概率可靠性分析法和概率分析法对跃龙门隧道3#斜井的突水问题进行了分析。并与现场实测结果对比验证,结果表明本文提出的临界安全厚度的确定方法较可靠,进一步完善了隧道突水防突结构的确定方法。 (4)本文主要考虑隧道前方较完整围岩的突水破坏问题,而现实中更可能遇到的是非完整围岩的裂隙突水问题。因此,后续有必要针对非完整围岩的突水问题进行分析。
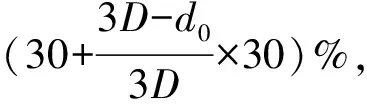


2 工程案例分析及讨论
2.1 工程背景

2.2 岩体参数值及范围确定


2.3 基于不确定性的隔水岩层厚度的分析


3 结论

