渗流井辐射管-含水层间水量交换数值模拟研究

畅俊斌，柯贤敏，王 玮,葛佳亮，田国林

(1.陕西地矿九0八水文地质工程地质大队，陕西 西安 710600；2.陕西省矿产资源勘与综合利用重点实验室，陕西 西安 710054；3.中煤能源研究院有限责任公司，陕西 西安 710054；4.长安大学环境科学与工程学院，陕西 西安 710054；5.旱区地下水与生态效应教育部重点实验室，陕西 西安 710054)

渗流井取水工程是近年来兴起的复杂取水构筑物，利用河床表面覆盖的砂石层净化河水，将河水转化成地下水，从而获得水资源的取水工程[1]。渗流井取水工程因其低耗、高产、易于管理等优点[2]被广泛应用。长期以来，大多研究者将井管概化为等强度线汇的第二类井孔边界条件[3～6]，由于水流会产生水头损失，故井管并不是等水头边界。陈崇希等[7]提出“渗流-管流耦合模型”，将辐射管内外渗流管流很好地耦合起来，便于计算渗流井出水量。Eunhee Lee等[8]利用经验系数刻画水平井管并根据不同雷诺数下内摩擦力的经验公式，计算由于摩擦产生的水头损失。刘基[9]针对以往模型的不足，建立改进的渗流井计算模型，计算多个渗流井同时工作时的出水量。徐嘉璐[10]通过大型砂槽物理模拟试验，研究大降深条件下渗流井取水造成河水位与地下水位脱节现象，确定了河水位与地下水位脱节的临界点及疏干单元的变化规律。王玮等[11～12]针对渗流井取水问题，在“等效渗透系数”和“渗流—管流耦合模型”等理论基础上，建立渗流井取水计算模型，并成功将该计算模型用于悖牛川水源地渗流井取水工程地下水允许开采量计算[2]。徐嘉璐等[13]以辐射管与含水层间交换水量为耦合点，进一步建立了改进渗流井取水计算模型，使得计算模型能够更精细地刻画辐射管特征，并实现多个渗流井同时取水的计算。之后改进的渗流井计算模型成功应用于陕北多个水源地计算中[14～15]。

以往渗流井计算模型中，辐射管-含水层间的水量交换系数大多通过反演得到，部分采用经验系数确定，未有准确的计算公式对其进行定量计算。辐射管与含水层间的交换量是渗流井出水量的唯一来源，是渗流井取水工程的重要环节，为此研究辐射管与含水层间的交换量具有重要意义。本文通过大型砂槽物理模拟试验，对渗流井取水的影响因素进行分析，推导出辐射管-含水层间水量交换系数的计算公式，并对部分试验方案建立数值模型，利用试验数据对数值模型可靠性及辐射管-含水层间水量交换系数计算公式的正确性进行验证。

1 试验方法与过程

1.1 试验装置

渗流砂槽长3.63 m，宽0.5 m，高1.17 m，砂槽顶端放置水箱，用于试验前期饱水及后期向砂槽内供水，砂槽左侧设置竖井，用于控制渗流井出水量。砂槽前后壁共设置18×10个水位观测孔，并插入不同长度的铜管(铜管另一端与测压板相连)，用于观测试验过程中砂槽内部不同位置的水位。试验装置示意图见图1。

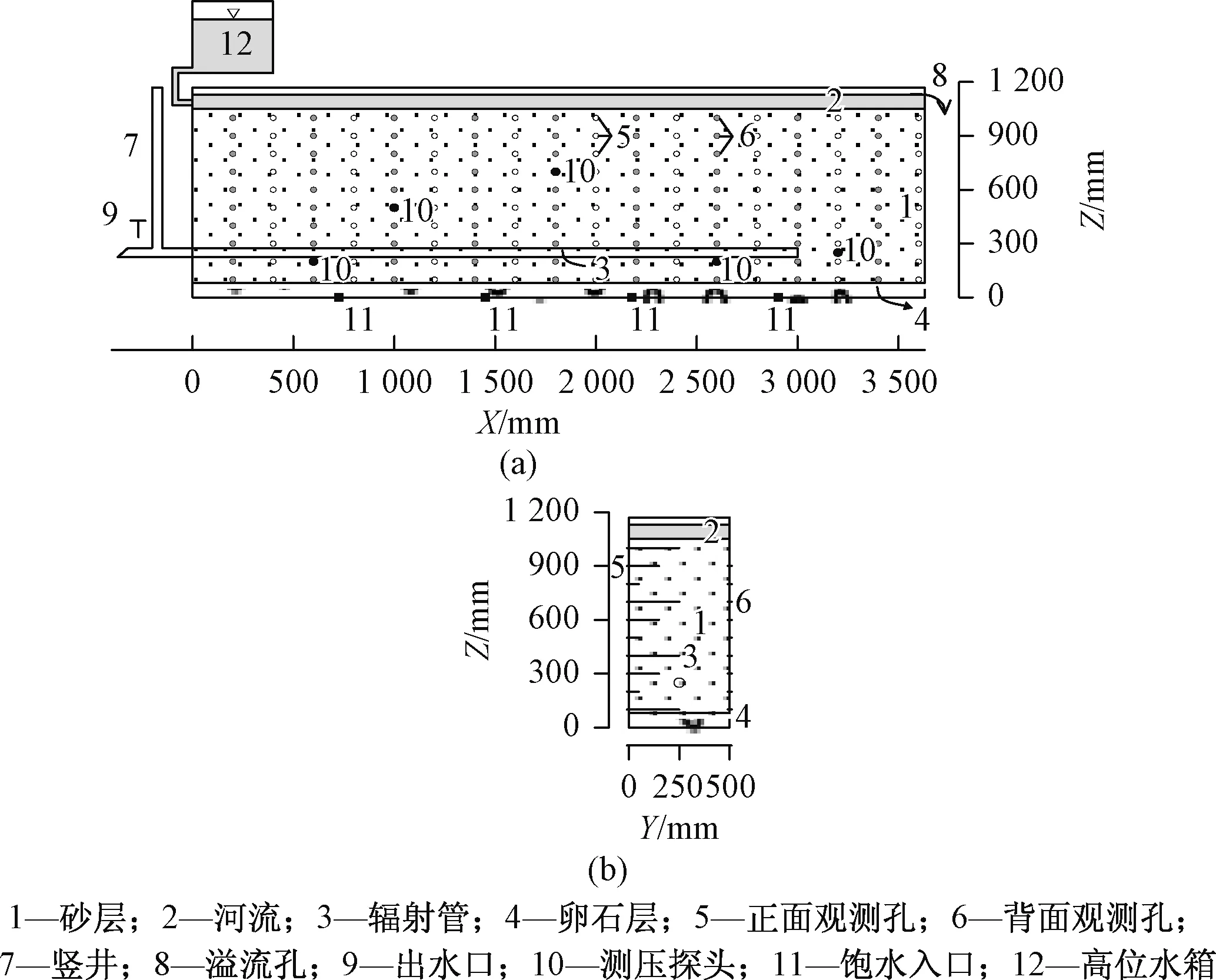
图1 试验装置示意图Fig.1 Design of the test equipment

1.2 试验方案设计

本次设计辐射管仰角为：0°、10°、13°(设计仰角为15°，由于工艺原因实际为13°)和30°，辐射管长度为：1 m、2 m、3 m。设计彩条布(由于彩条布隔水效果过强，本次沿x方向每隔40 cm，设置一列直径为0.5 cm的圆孔，圆孔间距为10 cm)和纱网(本次试验采用筛孔尺寸为1 mm的纱网)分别代表渗漏性能弱和强的河床类型。试验前期对上述部分方案进行了小、中、大3次竖井降深试验，后期经过改进对上述大多数方案进行自小而大5次竖井降深的试验。上述各条件互相组合，确定为设计试验方案。

1.3 试验过程

为了使辐射管内外呈现多种流态及方便试验装置的更换，本次砂槽物理模拟试验选择中粗砂(粒径为0.25～1.0 mm)为含水层介质。为了减少试验误差，对试验用砂进行水洗，去除杂质，采用水沉固结，分层装砂，以满足含水层均质的要求。试验结束后沿x轴(0～363 cm)进行6组竖管试验，测得竖直渗透系数依次为：28.81，37.81，38.89，40.07，46.73，33.50 m/d，该渗透系数可以为模型渗透系数(Kz)提供参考依据。

为了充分排除砂槽内空气，在砂槽底部装入一层卵石层，厚度约为8 cm，以便在饱水过程中，水能从砂槽底部自下而上进入含水层。装砂达到一定高度时，将一端用纱布包裹的铜管(长度：0.05 m、0.15 m、0.25 m)、渗流井微缩模型及测压探头进行安装，最终装砂总高度为0.97 m。装砂结束后，在砂层上布设彩条布(或尼龙纱网)，并在彩条布(或尼龙纱网)上铺一层均匀的卵石层，模拟河床介质。

饱水完成后，用洗耳球排除测压孔中的气泡，打开供水水箱的开关，使水流入“河流”中，当“河流”水位达到溢流高度时，记录测压孔、竖井、三角堰的初始水位。然后打开与竖井相连水龙头，调整与水龙头相连的橡胶管至第一次降深试验的竖井高度，记录此时的时间，即为试验初始时刻，待压力传感器上数据达到稳定后，记录三角堰的堰高、竖井的水位、并测量三角堰流量。记录频率为10 min/次，共记录5次，直到三角堰水位和竖井水位均稳定不变。重复上述实验过程，完成其他降深试验。

2 试验结果分析

由于试验方案和影响因素均较多，故采用逐步优选的方法对各影响因素进行分析，最终优选出取水效率最高的试验方案。

2.1 辐射管仰角对渗流井出水量影响

不同辐射管仰角条件下，渗流井出水量随竖井降深变化见图2。由图2可以看出，不论在强渗漏补给能力河流条件下还是在弱渗漏补给能力河流条件下，试验出水量随着竖井降深的增大均不断增大。当竖井降深增大时，导致辐射管内外水头差增大，含水层中水不断向辐射管流动，从而出水量增大。当其他取水条件相同时，辐射管仰角大的试验方案出水量大于辐射管仰角小的试验方案出水量。这是由于随着辐射管仰角的增大，相同长度辐射管在水平方向上投影长度相差不大，但在竖直方向上的投影长度越大，辐射管影响面积增大。同时，辐射管仰角越大，辐射管末端距河流越近，容易接受河流渗漏补给，从而渗流井出水量大。

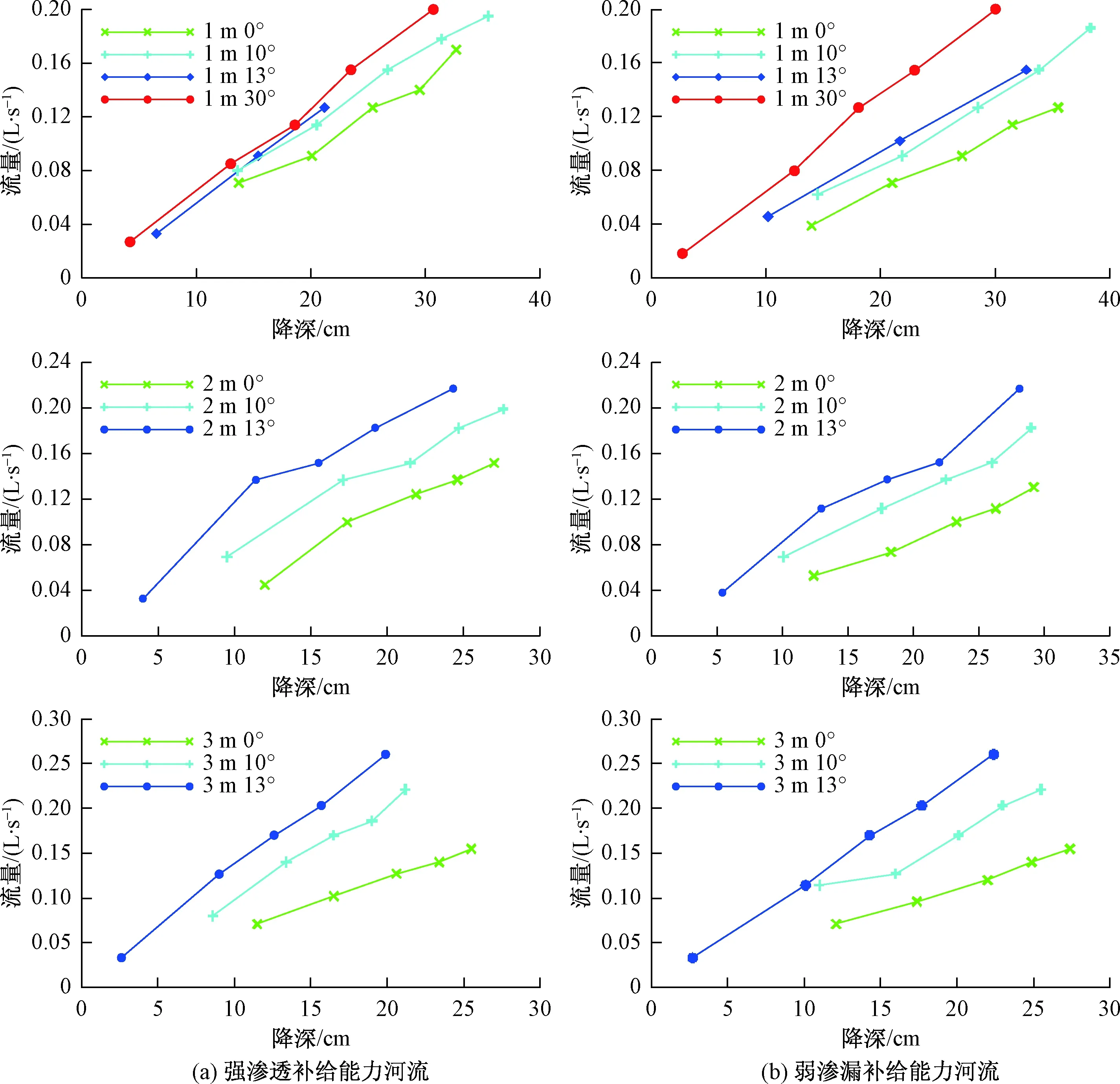
图2 不同辐射管仰角条件下渗流井出水量随竖井降深变化图Fig.2 Water yield of the seepage well with the drawdown of vertical shaft under different elevation angles of the radiant tube

鉴于试验装置限制，辐射管仰角为30°方案只进行了1 m试验。故对取水效率较高的辐射管仰角为13°的方案进行分析，研究该方案下辐射管长度及河床类型对渗流井出水量的影响。

2.2 辐射管长度对渗流井出水量影响

在出水效果较好的13°方案基础上，分析辐射管长度对渗流井取水效果的影响，结果见图3。

由图3可知，随着竖井降深增大，试验出水量也不断增大。不同渗漏补给作用下，当竖井降深相同时，随着辐射管长度的增加，渗流井出水量也不断增大。辐射管长度越长，辐射管与含水层接触面积就越大，且在辐射管仰角存在的情况下，辐射管末端距河更近，更容易接受河流的渗漏补给，在竖直方向也增大了与含水层的接触面积，从而出水量较大。可见本次试验方案中3 m 13°方案优于其他长度取水方案。

2.3 河床类型对取水构筑物取水效果的影响分析

在辐射管仰角及辐射管长度研究的基础上，选择出水效果较好的3 m 13°方案，进行河床类型对渗流井取水效果的影响分析，结果见图4。

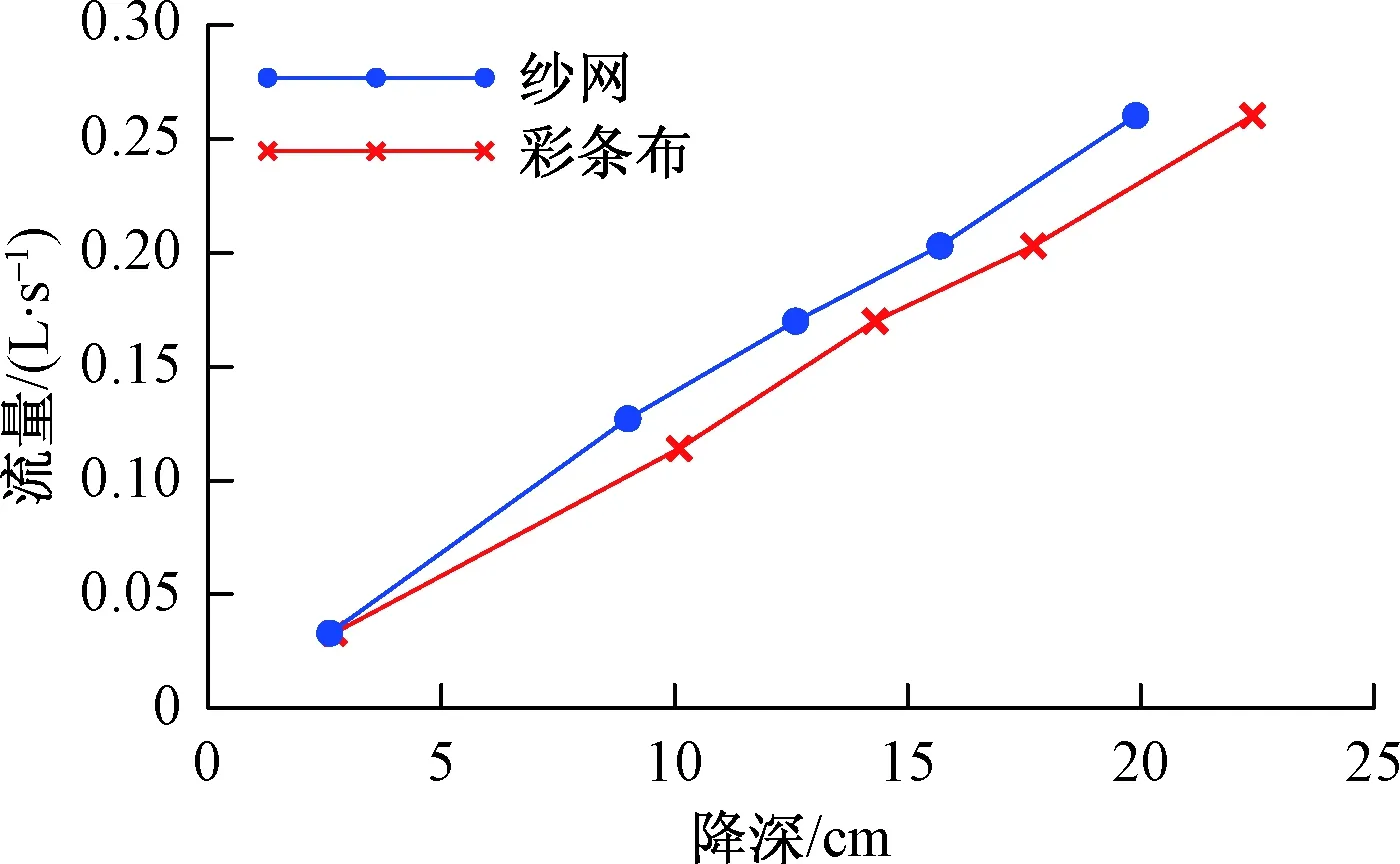
图4 不同河流类型作用下试验出水量随竖井降深变化图Fig.4 Water yield of the seepage well with the drawdown of vertical shaft in different rivers

由图4可以看出，在辐射管仰角和辐射管长度相同条件下，随着竖井降深的增大，试验出水量不断增大，且强渗漏补给能力河流方案的试验出水量大于弱渗漏补给能力河流方案的试验出水量。两种试验方案下，仅因为河床介质不同即河床渗透系数不同，获得河流补给量不同。河流渗漏补给量为：

(1)

式中：Q——河流渗漏补给量；

Kz——河床垂向渗透系数；

M——河床介质厚度；

A——河流发生渗漏的面积；

ΔH——河流与含水层间的水头差。

由式(1)可以看出，两种河流试验方案中，除了河床的渗透系数不同外，其他各项均相等。可见河床渗漏补给量受河床的渗透系数影响，河床渗透系数越大，河流渗漏补给量越大，渗流井出水量越大。

3 数值模拟

3.1 辐射管-含水层交换系数推导

辐射管与含水层的交换量计算公式可用达西定律表示，水头可采用迭代法求解，故而问题转化为确定辐射管-含水层间的交换系数C：

Qex=Cj,i,k(hin-hj,i,k)

(2)

式中:Qex——辐射孔与含水层间交换量；

hin——节点in的水头；

hj,i,k——单元格(j,i,k)的水头；

Cj,i,k——辐射管-含水层间的水量交换系数。

Shoemaker[16]提出均质各向同性介质条件下辐射管与含水层间水量交换系数计算公式：

(3)

式中：Kj,i,k——辐射管所在单元格(j,i,k)的渗透系数；

dip——与节点in相连的管道ip的直径；

Δlip——与管道ip相连的两个管道节点的直线距离；

τip——管道ip相邻节点in的曲率；

rip——辐射管的半径。

式(3)中Cj,i,k值计算公式只适用于均质各向同性介质且缺少试验验证，其正确性有待考证。实际工程中，含水层介质大多不是均质各向同性，故均质各向异性条件下的C1值的计算对指导渗流井的设计、模型的建立和计算具有重要意义。本文在式(3)的基础上，先分别根据Kx、Ky和Kz计算出Cx、Cy、Cz。然后得到Cx、Cy、Cz垂直辐射管的分量，然后将各分量相乘开方：

(4)

式中：α——辐射管仰角；

n——与辐射管节点i相连的节点总个数。

以往的辐射管-含水层间的交换系数均是通过试算法、经验公式及参数反演得出，未有定量的计算公式。本文推导出C1值计算公式，并建立数值模型，将计算公式应用于模型中，通过试验数据对模型及计算公式进行验证。

3.2 数值模型

3.2.1概念模型

本次以整个砂槽为模拟区，即X：0～3.63 m；Y：0～0.5 m；Z：0～1.13 m。将含水层介质概化成均质轴对称各向异性多孔介质；由于强渗漏补给能力河流(纱网方案)对水流下渗阻碍作用很小，将其概化为定水头边界；弱渗漏补给能力河流(彩条布方案)对水流下渗阻碍作用比较明显，将其概化为河流边界。砂槽四壁及底部为钢板，将其概化为隔水边界。试验过程中，稳定时刻的竖井水位保持不变，将其概化为定水头，由于竖井位于砂槽外部，故将竖井与平巷相连处单元格设置为定水头。试验开始后，砂槽内含水层只接受河流补给，竖井水位下降后，地下水从各个方向向辐射管汇集，通过与竖井相连的平巷流入三角堰，整个过程中，地下水流动形态呈现显著的三维流特征，水流运动规律服从达西定律。

3.2.2数学模型

在上述概念模型分析的基础上，建立本次砂槽物理模拟试验地下水三维稳定流数学模型：

式中：H——地下水位标高/m；

x、y、z——坐标变量/m；

K——含水层渗透系数/(m·d-1)；

D——模拟区的范围；

Γ2——第二类边界；

n——隔水边界的外法线方向；

np——潜水面边界的内法线方向；

C1——辐射管与含水层间交换系数/(m2·d-1)；

Qe——辐射孔-含水层间的交换量/(m3·d-1)；

Qp——辐射管内出水量/(m3·d-1)；

Hr——河水位/m；

ΔH——水头损失/m；

Hp——辐射管内水位/m；

ν——水流运动黏滞系数/(m2·s-1)；

d——辐射管的直径/m；

v——渗流速度/(m·s-1)；

Kr——河床介质渗透系数；

Mr——河床介质厚度/m；

qr——河流渗漏补给量/(m3·d-1)。

管流计算公式中包含有水头、流速、流量等多个变量，可采用迭代法进行求解。可通过把含水层与渗流井间的交换量作为汇项把该方程耦合进MODFLOW。计算时，先把各管道节点的顶部标高作为渗流井井管内水头迭代初值，并假设初始流态为层流，在此基础上，结合MODFLOW中含水层水头的迭代初值，计算出含水层与渗流井间的交换量，进而可计算出井管内各段的流量变化。根据这个流量及井管直径，可计算井管内水流的雷诺数，据此选择不同的管流公式可以计算出新的管内水头分布，再利用新的管内水头值重复上述计算，直到连续两次迭代的井管内水头值绝对误差满足精度为止。此时含水层与水平井间交换量可作为汇项加入到渗流方程中，采用MODFLOW中的迭代可求解出含水层水头，再将迭代出的含水层水头作为MODFLOW中含水层水头的迭代初值，重复上述迭代计算过程，直至连续两次迭代的含水层水头值绝对误差满足精度要求为止。再利用辐射管与含水层间水量交换系数、最终确定的含水层水头及井管内的水头得出渗流井出水量。其中，MODFLOW软件通过CFP文件将模型与离散的管道耦合起来，井管由大量管道及节点组成，通过设置每个管道节点的高程及管道参数(辐射管与含水层间水量交换系数、弯曲度、粗糙度、层流与紊流相互转换的两个临界雷诺数、管径等)并将其编号来模拟实际管道。

3.2.3数值模型

采用有限差分法，对模拟区进行网格剖分，垂向上砂槽顶部的“河流”占一层、底部的卵石层占2层，河流与卵石层厚度均为8 cm，中间含水层共分28层。整个模拟区沿X轴方向被剖分为92列，沿Y轴方向被剖分为12行，沿Z轴方向被剖分为31层(第25层为平巷所在层)，单层活动单元共1 104个，总活动单元数为34 224个。在改进的渗流井计算模型基础上，以辐射管-含水层间交换量为耦合点，建立“渗流-管流耦合模型”，利用稳定状态下测得的渗流井出水量、竖井降深及观测孔实测降深与模型计算结果进行拟合，验证模型可靠性。

3.3 数值模拟结果分析

本次对3 m 13°两种河流方案进行数值模拟，模拟结果见表1。

由表1可以看出，渗流井出水量的实测值与模型计算值近似一致，强渗漏补给河流方案实测流量与模型计算流量相对误差差值范围在-6.36%～4.88%。弱渗漏补给河流方案实测流量与模型计算流量的相对误差值范围在-4.56%～2.42%。由图5可知，模型计算结果与实测结果的“流量-降深”曲线基本重合，拟合良好。且随着竖井降深的增加渗流井出水量也增大，这与试验得到规律一致。

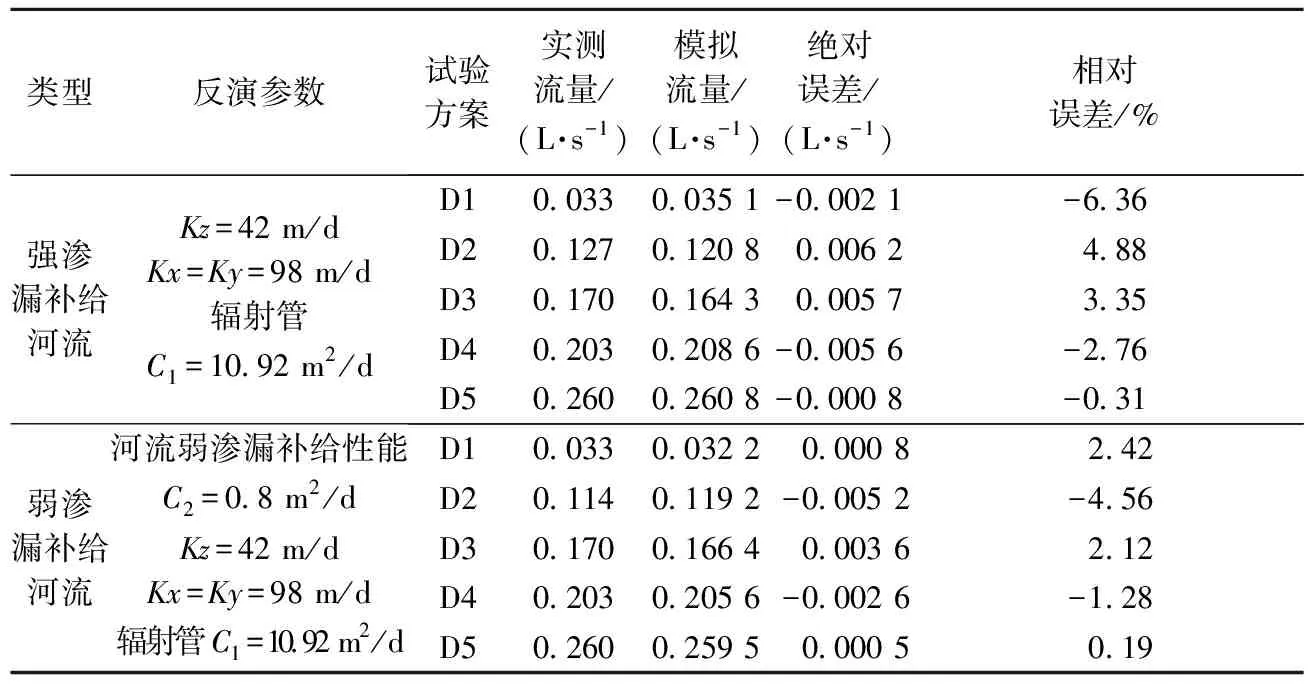
表1 流量拟合结果表Table 1 Fitting results of the flow

注：表1中D1-D5分别表示第一次—第五次降深试验。

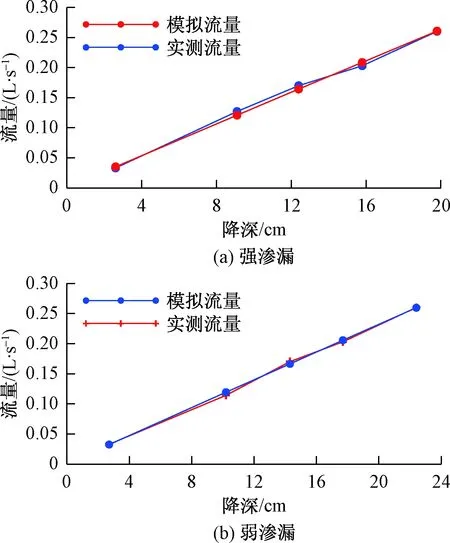
图5 强渗漏和弱渗漏补给河流出水量拟合曲线Fig.5 The fitting curve of strong and weak leakage capacity river

为进一步验证所建模型的合理性，本次对测压板观测孔水位降深与模型计算降深也进行拟合(以第一、三、五次降深为例绘图)，拟合结果见图6。

由图6可以看出，除个别观测点外，各观测孔计算水位降深与实测降深组合的点均位于y=x+0.03与y=x-0.03之间，说明模型计算降深值与实测降深值的误差在-0.03～0.03 m之间。对于小降深条件下，误差仅为0.005 m。且从图中还可看出，随着竖井降深的增大，砂槽内各观测点的降深也变大，可见当竖井降深增大时，含水层中的水均向辐射管流动，从而导致各观测点水位降深增大，当竖井降深增大时，辐射管的影响面积也变大。

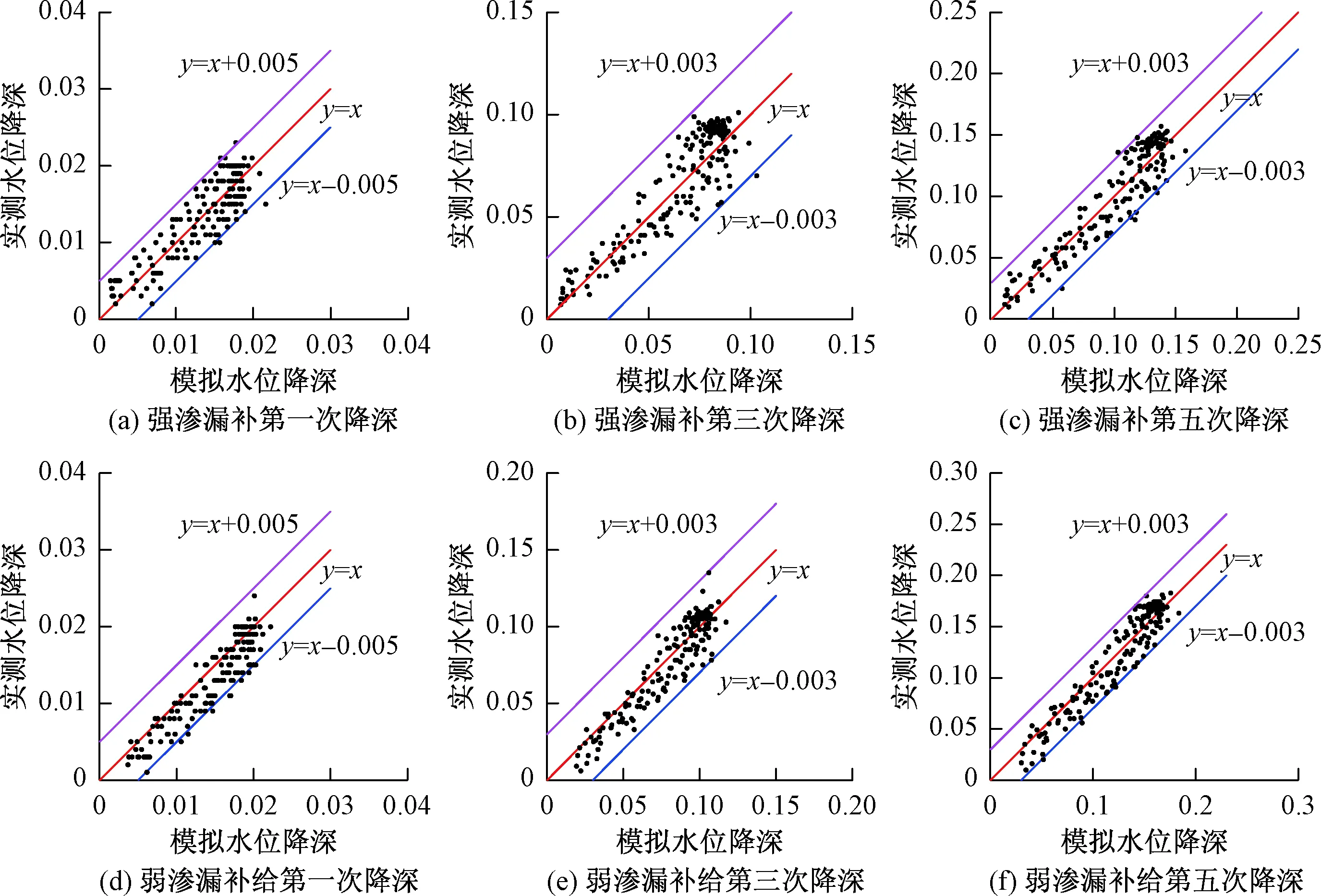
图6 强渗漏和弱渗漏补给河流测压点水位降深拟合结果Fig.6 Fitting results of the pressure observation drawdown in strong and weak leakage capacity rivers

由表1及图5可以看出实测流量与模型计算流量近于一致，由图6可以看出，各观测孔模型计算降深与试验实测降深误差很小，满足模型精度要求。由此可知，试验实测结果与模型计算结果拟合良好，说明本次所建模型是合理的，辐射管-含水层间水量交换系数计算公式是可行的。

4 结论

(1)其他条件不变，随着竖井降深的增大，辐射管仰角的增大，辐射管长度的增加，河流渗漏补给能力的增强，渗流井出水量均不断增大。

(2)在本次物理模拟试验中，3 m 13°强渗漏补给能力河流方案为取水效果最佳方案。

(3)在以往研究的基础上，推导出了适用于均质轴对称各项异性介质条件下的辐射管-含水层水量交换系数的计算公式。